4.4: Comprender la pendiente de una línea
- Page ID
- 110249
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Al final de esta sección, podrás:
- Usar geotableros para modelar taludes
- Se usa\(m = \frac{\text{rise}}{\text{run}}\) para encontrar la pendiente de una línea a partir de su gráfica
- Encuentra la pendiente de líneas horizontales y verticales
- Utilice la fórmula de pendiente para encontrar el talud de una línea entre dos puntos
- Graficar una línea dada un punto y la pendiente
- Resolver aplicaciones de pendientes
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(\frac{1 - 4}{8 - 2}\).
Si te perdiste este problema, revisa Ejercicio 1.6.31 - Dividir:\(\frac{0}{4}, \frac{4}{0}\).
Si te perdiste este problema, revisa el Ejercicio 1.10.16. - Simplificar:\(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\).
Si te perdiste este problema, revisa el Ejercicio 1.6.4.
Cuando graficas ecuaciones lineales, puedes notar que algunas líneas se inclinan hacia arriba a medida que van de izquierda a derecha y algunas líneas se inclinan hacia abajo. Algunas líneas son muy empinadas y algunas líneas son más planas. ¿Qué determina si una línea se inclina hacia arriba o hacia abajo o si es empinada o plana?
En matemáticas, la 'inclinación' de una línea se denomina pendiente de la línea. El concepto de talud tiene muchas aplicaciones en el mundo real. El cabeceo de un techo, la pendiente de una autopista y una rampa para una silla de ruedas son algunos ejemplos en los que literalmente se ven pendientes. Y cuando montas en bicicleta, sientes la pendiente mientras bombeas cuesta arriba o cuesta abajo en la costa.
En esta sección, exploraremos el concepto de pendiente.
Uso de geoplacas para modelar taludes
Un geoboard es un tablero con una rejilla de clavijas en él. El uso de bandas de goma en una geoplaca nos da una forma concreta de modelar líneas en una cuadrícula de coordenadas. Al estirar una banda de goma entre dos clavijas en una geobordo, podemos descubrir cómo encontrar la pendiente de una línea.
Hacer la actividad de Matemáticas Manipulativas “Explorando Pendiente” te ayudará a desarrollar una mejor comprensión de la pendiente de una línea. (Se puede usar papel cuadriculado en lugar de geobordo, si es necesario).Comenzaremos estirando una banda de goma entre dos clavijas como se muestra en la Figura\(\PageIndex{1}\).
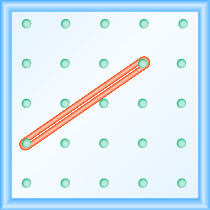
¿No parece una línea?
Ahora estiramos una parte de la goma recta hacia arriba desde la clavija izquierda y alrededor de una tercera clavija para hacer los lados de un triángulo rectángulo, como se muestra en la Figura\(\PageIndex{2}\)
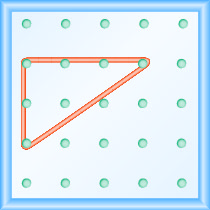
Hacemos cuidadosamente un ángulo de 90º alrededor de la tercera clavija, por lo que una de las líneas recién formadas es vertical y la otra es horizontal.
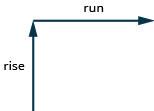
Para encontrar la pendiente de la línea, medimos la distancia a lo largo de los lados vertical y horizontal del triángulo. A la distancia vertical se le llama subida y a la distancia horizontal se le llama recorrido, como se muestra en la Figura\(\PageIndex{3}\).
Si nuestro geoboard y goma elástica se ven igual que el que se muestra en la Figura\(\PageIndex{4}\), la subida es 2. La banda de goma sube 2 unidades. (Cada espacio es una unidad.)
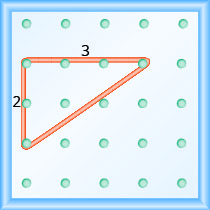
El ascenso en este geobordo es de 2, ya que la banda elástica sube dos unidades.
¿Cuál es la carrera?
La banda de goma atraviesa 3 unidades. La carrera es 3 (ver Figura\(\PageIndex{4}\)).
La pendiente de una línea es la relación entre la subida y la carrera. En matemáticas, siempre se le hace referencia con la letra m.
La pendiente de una línea de una línea es\(m = \frac{\text{rise}}{\text{run}}\).
La subida mide el cambio vertical y la corrida mide el cambio horizontal entre dos puntos de la línea.
¿Cuál es la pendiente de la línea en el geobordo en la Figura\(\PageIndex{4}\)?
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]
La línea tiene pendiente\(\frac{2}{3}\). Esto significa que la línea sube 2 unidades por cada 3 unidades de carrera.
Cuando trabajamos con geoboards, es una buena idea adquirir el hábito de comenzar por una clavija a la izquierda y conectarnos a una clavija a la derecha. Si la subida sube es positiva y si baja es negativa. La carrera irá de izquierda a derecha y será positiva.
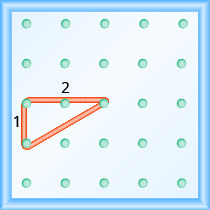
¿Cuál es la pendiente de la línea en el geobordo que se muestra?
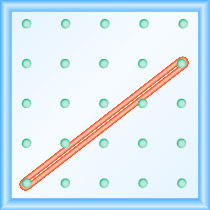
- Contestar
-
Utilice la definición de pendiente:\(m = \frac{\text{rise}}{\text{run}}\).
Comienza por la clavija izquierda y cuenta los espacios hacia arriba y hacia la derecha para llegar a la segunda clavija.
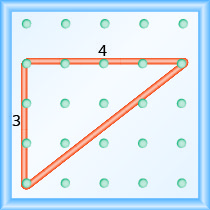
\[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]
Esto significa que la línea sube 3 unidades por cada 4 unidades de carrera.
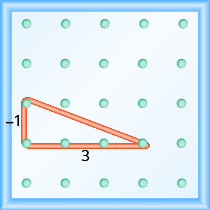
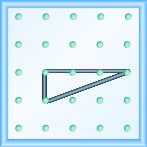
¿Cuál es la pendiente de la línea en el geobordo que se muestra?
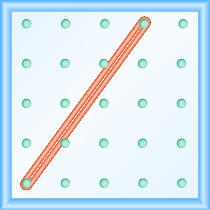
- Contestar
-
\(\frac{4}{3}\)
¿Cuál es la pendiente de la línea en el geobordo que se muestra?
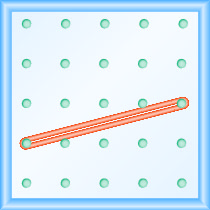
- Contestar
-
\(\frac{1}{4}\)
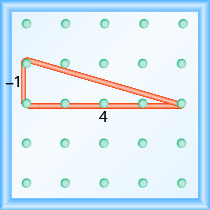
¿Cuál es la pendiente de la línea en el geobordo que se muestra?
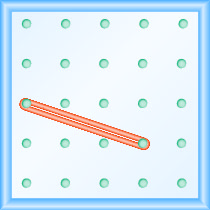
- Contestar
-
Utilice la definición de pendiente:\(m = \frac{\text{rise}}{\text{run}}\).
Comienza por la clavija izquierda y cuenta las unidades hacia abajo y hacia la derecha para llegar a la segunda clavija.
\[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]
Esto significa que la línea cae 1 unidad por cada 3 unidades de carrera.
¿Cuál es la pendiente de la línea en el geobordo?
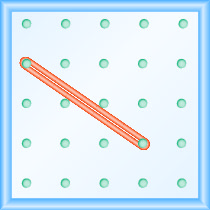
- Contestar
-
\(-\frac{2}{3}\)
¿Cuál es la pendiente de la línea en el geobordo?
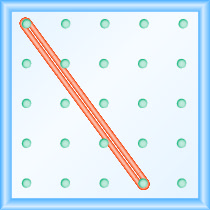
- Contestar
-
\(-\frac{4}{3}\)
Observe que en Ejercicio\(\PageIndex{1}\) la pendiente es positiva y en Ejercicio\(\PageIndex{4}\) la pendiente es negativa. ¿Observa alguna diferencia en las dos líneas que se muestran en la Figura (a) y la Figura (b)?
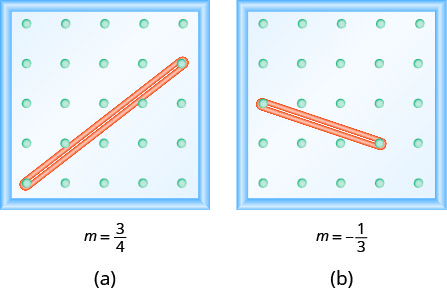
Nosotros 'leemos' una línea de izquierda a derecha igual que leemos palabras en inglés. Al leer de izquierda a derecha, la línea de la Figura (a) va subiendo; tiene pendiente positiva. La línea de la Figura (b) va bajando; tiene pendiente negativa.
Utilice un geoboard para modelar una línea con pendiente\(\frac{1}{2}\).
- Contestar
-
Para modelar una línea en una geobordo, necesitamos el ascenso y la carrera.
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)
La hipotenusa del triángulo rectángulo formado por la banda elástica representa una línea cuya pendiente es\(\frac{1}{2}\).
Modelar la pendiente\(m = \frac{1}{3}\). Haz un dibujo para mostrar tus resultados.
- Contestar
-
Modelar la pendiente\(m = \frac{3}{2}\). Haz un dibujo para mostrar tus resultados.
- Contestar
-
Utilice un geoboard para modelar una línea con pendiente\(\frac{-1}{4}\).
- Contestar
-
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}\)
La hipotenusa del triángulo rectángulo formado por la banda elástica representa una línea cuya pendiente es\(\frac{-1}{4}\).
Modelar la pendiente\(m = \frac{-2}{3}\). Haz un dibujo para mostrar tus resultados.
- Contestar
-
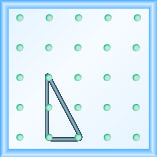
Modelar la pendiente\(m = \frac{-1}{3}\). Haz un dibujo para mostrar tus resultados.
- Contestar
-
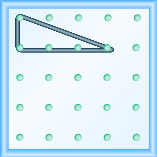
Utilizar\(m = \frac{\text{rise}}{\text{run}}\) para encontrar la pendiente de una línea a partir de su gráfica
Ahora, veremos algunas gráficas en el plano de coordenadas XY y veremos cómo encontrar sus pendientes. El método será muy similar al que acabamos de modelar en nuestras geoplacas.
Para encontrar la pendiente, debemos contar la subida y la carrera. Pero, ¿por dónde empezamos?
Localizamos dos puntos en la línea cuyas coordenadas son números enteros. Luego comenzamos con el punto de la izquierda y dibujamos un triángulo rectángulo, para que podamos contar la subida y la carrera.
Encuentra la pendiente de la línea que se muestra.
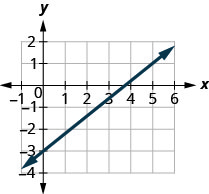
- Contestar
-
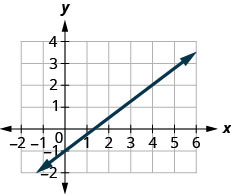
Encuentra la pendiente de la línea que se muestra.
- Contestar
-
\(\frac{2}{5}\)
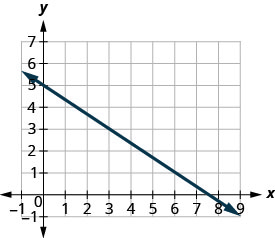
Encuentra la pendiente de la línea que se muestra.
- Contestar
-
\(\frac{3}{4}\)
- Localice dos puntos en la línea cuyas coordenadas sean números enteros.
- Comenzando por el punto de la izquierda, esboza un triángulo rectángulo, yendo del primer punto al segundo punto.
- Cuenta la subida y la carrera en las piernas del triángulo.
- Tomar la proporción de subida a correr para encontrar la pendiente,\(m = \frac{\text{rise}}{\text{run}}\).
Encuentra la pendiente de la línea que se muestra.
- Contestar
-
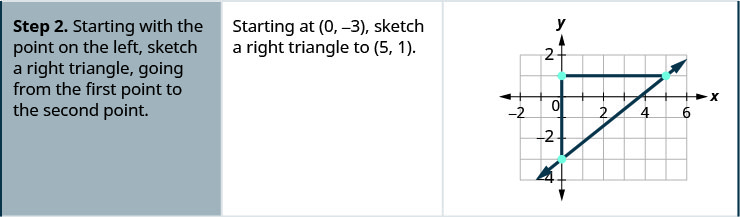
Localice dos puntos en la gráfica cuyas coordenadas sean números enteros. (0,5) y (3,3) ¿Qué punto está a la izquierda? (0,5) A partir de (0,5), dibuje un triángulo rectángulo a (3,3).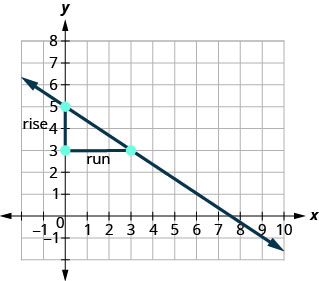 
Contar el aumento, es negativo. La subida es −2. Cuenta la carrera. La carrera es 3. Utilice la fórmula de pendiente. \(m = \frac{\text{rise}}{\text{run}}\) Sustituir los valores de la subida y corrida. \(m = \frac{-2}{3}\) Simplificar. \(m = -\frac{2}{3}\) La pendiente de la línea es\(-\frac{2}{3}\). Entonces y aumenta en 3 unidades a medida que xx disminuye en 2 unidades.
¿Y si usamos los puntos (−3,7) y (6,1) para encontrar la pendiente de la línea?
-
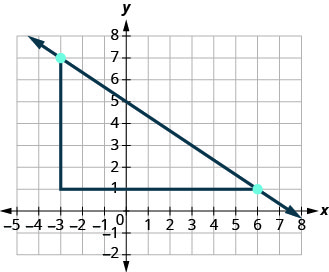
El ascenso sería −6 y la carrera sería 9. Entonces\(m = \frac{-6}{9}\), y eso simplifica a\(m = -\frac{2}{3}\). Recuerda, no importa qué puntos uses, la pendiente de la línea siempre es la misma.
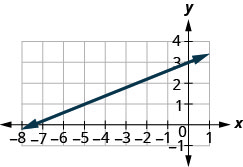
Encuentra la pendiente de la línea que se muestra.
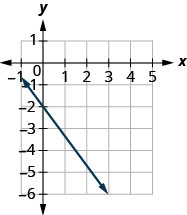
- Contestar
-
\(-\frac{4}{3}\)
Encuentra la pendiente de la línea que se muestra.
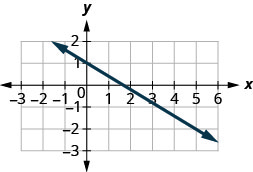
- Contestar
-
\(-\frac{3}{5}\)
En los dos últimos ejemplos, las líneas tenían y -intercepciones con valores enteros, por lo que fue conveniente usar la intercepción y como uno de los puntos para encontrar la pendiente. En el siguiente ejemplo, la intercepción y es una fracción. En lugar de usar ese punto, buscaremos otros dos puntos cuyas coordenadas sean números enteros. Esto facilitará los cálculos de taludes.
Encuentra la pendiente de la línea que se muestra.
- Contestar
-
Localice dos puntos en la gráfica cuyas coordenadas sean números enteros. (2,3) y (7,6) ¿Qué punto está a la izquierda? (2,3) Comenzando en (2,3), dibuje un triángulo rectángulo a (7,6).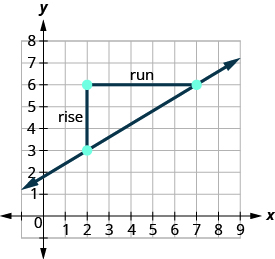 
Cuenta la subida. El ascenso es de 3. Cuenta la carrera. La carrera es 5. Utilice la fórmula de pendiente. \(m = \frac{\text{rise}}{\text{run}}\) Sustituir los valores de la subida y corrida. \(m = \frac{3}{5}\) La pendiente de la línea es\(\frac{3}{5}\). Esto significa que y aumenta 5 unidades a medida que x aumenta 3 unidades.
Cuando usamos geoboards para introducir el concepto de pendiente, dijimos que siempre empezaríamos con el punto de la izquierda y contaríamos la subida y la carrera para llegar al punto de la derecha. De esa manera la carrera siempre fue positiva y la subida determinó si la pendiente era positiva o negativa.
¿Qué pasaría si empezáramos con el punto de la derecha?
Usemos nuevamente los puntos (2,3) y (7,6), pero ahora comenzaremos en (7,6).
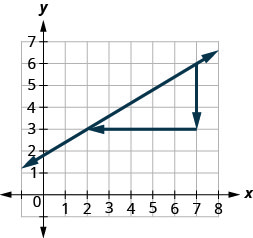
- \(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
- No importa por dónde empieces, la pendiente de la línea es siempre la misma.
Encuentra la pendiente de la línea que se muestra.
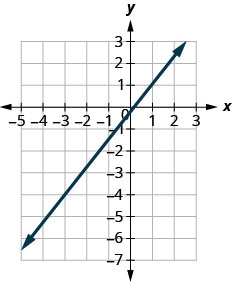
- Contestar
-
\(\frac{5}{4}\)
Encuentra la pendiente de la línea que se muestra.
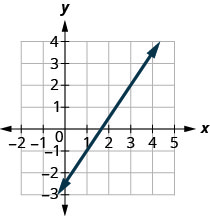
- Contestar
-
\(\frac{3}{2}\)
Encuentra la Pendiente de Líneas Horizontales y Verticales
¿Recuerdas qué tenían de especial las líneas horizontales y verticales? Sus ecuaciones solo tenían una variable.
\[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]
Entonces, ¿cómo encontramos la pendiente de la línea horizontal y=4y=4? Una aproximación sería graficar la línea horizontal, encontrar dos puntos en ella, y contar la subida y la carrera. Veamos qué pasa cuando hacemos esto.
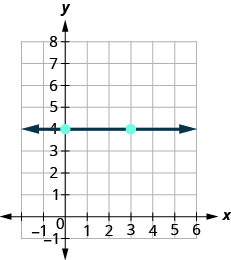
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)
Todas las líneas horizontales tienen pendiente 0. Cuando las coordenadas y son las mismas, la subida es 0.
La pendiente de una línea horizontal, y=b, es 0.
El piso de tu habitación es horizontal. Su pendiente es 0. Si colocas cuidadosamente una pelota en el piso, no se rodaría.
Ahora, consideraremos una línea vertical, la línea.
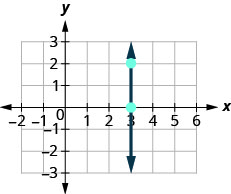
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)
Pero no podemos dividir por 0. La división por 0 no está definida. Entonces decimos que la pendiente de la línea vertical x=3x=3 es indefinida.
La pendiente de cualquier línea vertical es indefinida. Cuando las coordenadas x de una línea son todas iguales, la ejecución es 0.
La pendiente de una línea vertical, x=a, es indefinida.
Encuentra la pendiente de cada línea:
ⓐ x=8 ⓑ y=−5.
- Contestar
-
ⓐ x=8
Esta es una línea vertical.
Su pendiente es indefinida.
ⓑ y=−5
Esta es una línea horizontal.
Tiene pendiente 0.
Encuentra la pendiente de la línea: x=−4.
- Contestar
-
undefined
Encuentra la pendiente de la línea: y=7.
- Contestar
-
0
Recuerda, 'leemos' una línea de izquierda a derecha, al igual que leemos palabras escritas en inglés.
Utilice la fórmula de pendiente para encontrar la pendiente de una línea entre dos puntos
Hacer la actividad de Matemáticas Manipulativas “Pendiente de Líneas Entre Dos Puntos” te ayudará a desarrollar una mejor comprensión de cómo encontrar la pendiente de una línea entre dos puntos.A veces necesitaremos encontrar la pendiente de una línea entre dos puntos cuando no tenemos una gráfica para contar la subida y la carrera. Podríamos trazar los puntos en papel de rejilla, luego contar la subida y la carrera, pero como veremos, hay una manera de encontrar la pendiente sin graficar. Antes de llegar a ella, necesitamos introducir alguna notación algebraica.
Hemos visto que un par ordenado (x, y) da las coordenadas de un punto. Pero cuando trabajamos con pendientes, utilizamos dos puntos. ¿Cómo se puede usar el mismo símbolo (x, y) para representar dos puntos diferentes? Los matemáticos utilizan subíndices para distinguir los puntos.
\[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]
El uso de subíndices en matemáticas es muy parecido al uso de las iniciales de apellido en la escuela primaria. ¿A lo mejor recuerdas a Laura C. y Laura M. en tu clase de tercer grado?
Utilizaremos\(\left(x_{1}, y_{1}\right)\) para identificar el primer punto y\(\left(x_{2}, y_{2}\right)\) para identificar el segundo punto.
Si tuviéramos más de dos puntos, podríamos usar\(\left(x_{3}, y_{3}\right)\),\(\left(x_{4}, y_{4}\right)\), y así sucesivamente.
Veamos cómo la subida y la carrera se relacionan con las coordenadas de los dos puntos al echar otro vistazo a la pendiente de la línea entre los puntos (2,3) y (7,6).
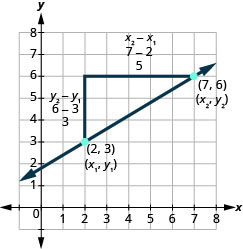
Ya que tenemos dos puntos, usaremos notación subíndice,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\).
En la gráfica, contamos la subida de 3 y la corrida de 5.
Observe que la subida de 3 se puede encontrar restando las coordenadas y 6 y 3.
\[3=6-3\]
Y la ejecución de 5 se puede encontrar restando las coordenadas x 7 y 2.
\[5 = 7 - 2\]
Lo sabemos\(m = \frac{\text{rise}}{\text{run}}\). Entonces\(m = \frac{3}{5}\).
Reescribimos la subida y corremos poniendo en las coordenadas\(m = \frac{6-3}{7-2}\)
Pero 6 es y2, la coordenada y del segundo punto y 3 es y1, la coordenada y del primer punto.
Así podemos reescribir la pendiente usando notación subíndice. \(m = \frac{y2-y1}{7-2}\)
Además, 7 es x2, la coordenada x del segundo punto y 2 es x1, la coordenada x del primer punto.
Entonces, nuevamente, reescribimos la pendiente usando notación subíndice. \(m = \frac{y2-y1}{x2-x1}\)
Hemos demostrado que en realidad\(m = \frac{y2-y1}{x2-x1}\) es otra versión de\(m = \frac{\text{rise}}{\text{run}}\). Podemos usar esta fórmula para encontrar la pendiente de una línea cuando tenemos dos puntos en la línea.
La pendiente de la línea entre dos puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\) es
\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
Esta es la fórmula de pendiente.
La pendiente es:
\[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]
Utilice la fórmula del talud para encontrar el talud de la línea entre los puntos (1,2) y (4,5).
- Contestar
-
\(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)
Confirmemos esto contando la pendiente en una gráfica utilizando\(m = \frac{\text{rise}}{\text{run}}\).
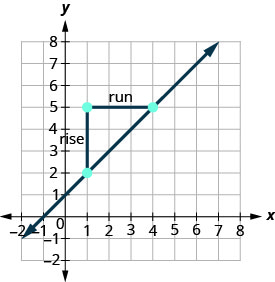
No importa a qué punto llame al punto #1 y a cuál llame al punto #2. La pendiente será la misma. Prueba el cálculo tú mismo.
Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través de los puntos: (8,5) y (6,3).
- Contestar
-
1
Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través de los puntos: (1,5) y (5,9).
- Contestar
-
1
Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través de los puntos (−2, −3) y (−7,4).
- Contestar
-
\(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)
Verifiquemos esta pendiente en la gráfica mostrada.
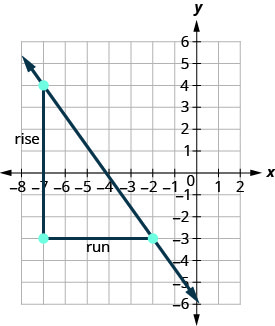
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]
Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través de los puntos: (−3,4) y (2, −1).
- Contestar
-
-1
Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través del par de puntos: (−2,6) y (−3, −4).
- Contestar
-
10
Graficar una línea dado un punto y el talud
Hasta ahora, en este capítulo, hemos graficado líneas trazando puntos, usando intercepciones y reconociendo líneas horizontales y verticales.
Otro método que podemos usar para graficar líneas se llama el método punto-pendiente. Utilizaremos este método cuando conozcamos un punto y la pendiente de la línea. Comenzaremos trazando el punto y luego usaremos la definición de pendiente para dibujar la gráfica de la línea.
Grafique la línea que pasa por el punto (1, −1) cuya pendiente es\(m = \frac{3}{4}\).
- Contestar
-
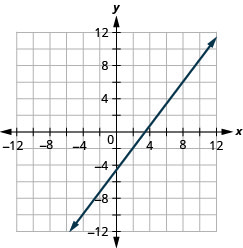
Grafique la línea que pasa por el punto (2, −2) con la pendiente\(m = \frac{4}{3}\).
- Contestar
-
Grafique la línea que pasa por el punto (−2,3) con la pendiente\(m=\frac{1}{4}\).
- Contestar
-
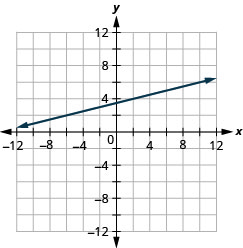
- Trazar el punto dado.
- Utilice la fórmula de pendiente\(m=\frac{\text { rise }}{\text { rise }}\) para identificar la subida y la carrera.
- Comenzando en el punto dado, cuente la subida y corra para marcar el segundo punto.
- Conecta los puntos con una línea.
Grafica la línea con y -intercept 2 cuya pendiente es\(m=−\frac{2}{3}\).
- Contestar
-
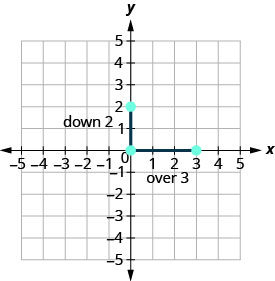
Trazar el punto dado, la intercepción y, (0,2).
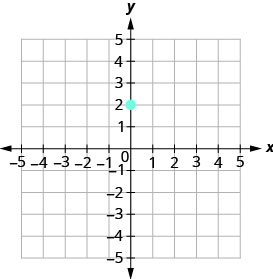
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)
Cuenta la subida y la carrera. Marcar el segundo punto.
-
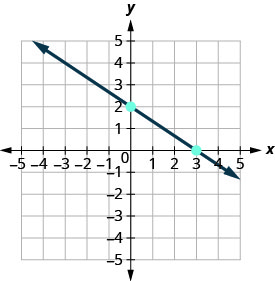
Conecta los dos puntos con una línea.
-
Puedes verificar tu trabajo encontrando un tercer punto. Ya que la pendiente es\(m=−\frac{2}{3}\), se puede escribir como\(m=\frac{2}{-3}\). Vuelva a (0,2) y cuente la subida, 2, y la carrera, −3.
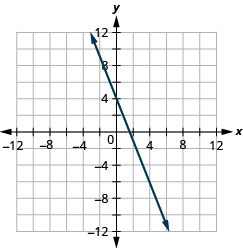
Grafica la línea con la intercepción y 4 y la pendiente\(m=−\frac{5}{2}\).
- Contestar
-
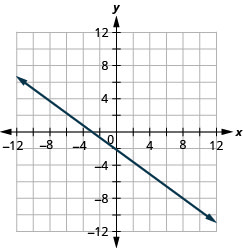
Grafica la línea con la intercepción x −3 y la pendiente\(m=−\frac{3}{4}\).
- Contestar
-
Grafica la línea que pasa por el punto (−1, −3) cuya pendiente es m=4.
- Contestar
-
Trazar el punto dado.
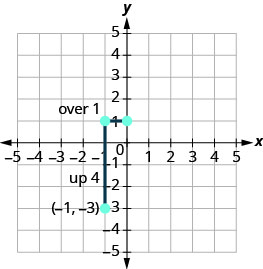
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}\)
Cuenta la subida y corre y marca el segundo punto.
-
Conecta los dos puntos con una línea.
-
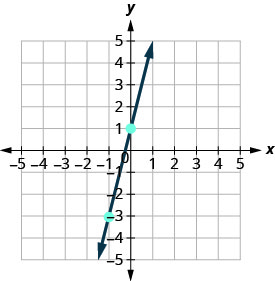
Puedes verificar tu trabajo encontrando un tercer punto. Dado que la pendiente es m=4, se puede escribir como\(m = \frac{-4}{-1}\). Vuelva a (−1, −3) y cuente la subida, −4, y la carrera, −1.
Grafica la línea con el punto (−2,1) y la pendiente m=3.
- Contestar
-
Grafica la línea con el punto (4, −2) y la pendiente m=−2.
- Contestar
-
Resolver aplicaciones de pendientes
Al inicio de esta sección, dijimos que hay muchas aplicaciones de talud en el mundo real. Echemos un vistazo a algunos ahora.
El 'paso' del techo de un edificio es la pendiente del techo. Conocer el terreno de juego es importante en climas donde hay fuertes nevadas. Si el techo es demasiado plano, el peso de la nieve puede hacer que se derrumbe. ¿Cuál es la pendiente de la cubierta que se muestra?
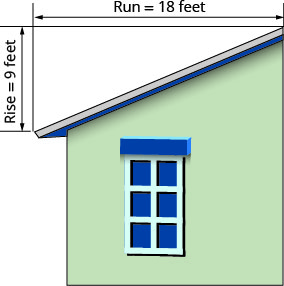
- Contestar
-
\(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)
Use Ejercicio\(\PageIndex{40}\), sustituyendo la subida = 14 y correr = 24.
- Contestar
-
\(\frac{7}{12}\)
Use Ejercicio\(\PageIndex{40}\), sustituyendo subida = 15 y carrera = 36.
- Contestar
-
\(\frac{5}{12}\)
¿Alguna vez has pensado en que las tuberías de aguas residuales van de tu casa a la calle? Deben inclinarse hacia abajo\(\frac{1}{4}\) pulgada por pie para drenar adecuadamente. ¿Cuál es la pendiente requerida?
- Contestar
-
\(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)
La tubería cae 1 pulgada por cada 48 pulgadas de recorrido horizontal.
Encuentra la pendiente de una tubería que se inclina hacia abajo\(\frac{1}{3}\) pulgadas por pie.
- Contestar
-
\(-\frac{1}{36}\)
Encuentra la pendiente de una tubería que desciende\(\frac{3}{4}\) pulgadas por yarda.
- Contestar
-
\(-\frac{1}{48}\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con comprensión de la pendiente de una línea.
Conceptos clave
- Encuentra la Pendiente de una Línea a partir de su Gráfica usando\(m=\frac{\text { rise }}{\text { run }}\)
- Localice dos puntos en la línea cuyas coordenadas sean números enteros.
- Comenzando por el punto de la izquierda, esboza un triángulo rectángulo, yendo del primer punto al segundo punto.
- Cuenta la subida y la carrera en las piernas del triángulo.
- Toma la proporción de subida para correr para encontrar la pendiente.
- Graficar una línea dado un punto y el talud
- Trazar el punto dado.
- Utilice la fórmula de pendiente\(m=\frac{\text { rise }}{\text { run }}\) para identificar la subida y la carrera.
- Comenzando en el punto dado, cuente la subida y corra para marcar el segundo punto.
- Conecta los puntos con una línea.
- Pendiente de una línea horizontal
- La pendiente de una línea horizontal, y=b, es 0.
- Pendiente de una línea vertical
- La pendiente de una línea vertical, x=a, es indefinida