4.4E: Ejercicios
- Page ID
- 110257
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La práctica hace la perfección
Uso de geoplacas para modelar taludes
En los siguientes ejercicios, encuentra la pendiente modelada en cada geobordo.
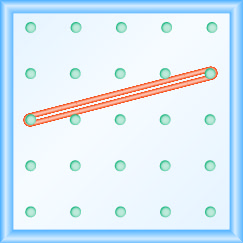
- Responder
-
\(\frac{1}{4}\)
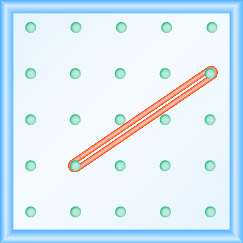
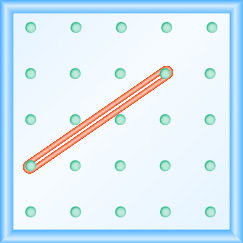
- Responder
-
\(\frac{2}{3}\)
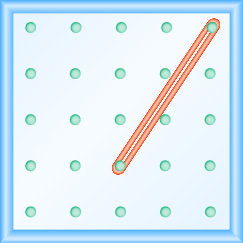
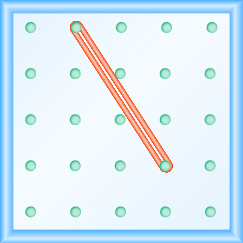
- Responder
-
\(\frac{-3}{2}=-\frac{3}{2}\)
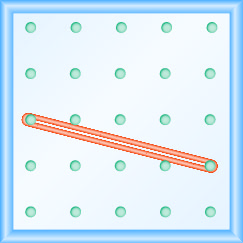
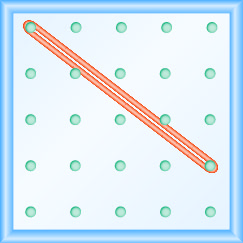
- Responder
-
\(-\frac{2}{3}\)
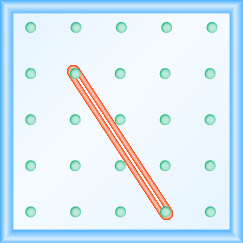
En los siguientes ejercicios, modele cada pendiente. Haz un dibujo para mostrar tus resultados.
\(\frac{2}{3}\)
- Responder
-
\(\frac{3}{4}\)
\(\frac{1}{4}\)
- Responder
-
\(\frac{4}{3}\)
\(-\frac{1}{2}\)
- Responder
-
\(-\frac{3}{4}\)
\(-\frac{2}{3}\)
- Responder
-
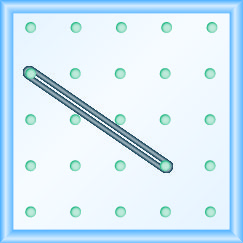
\(-\frac{3}{2}\)
Utilizar\(m=\frac{rise}{run}\) para encontrar la Pendiente de una Línea a partir de su Gráfica
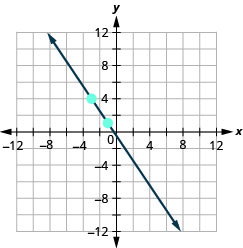
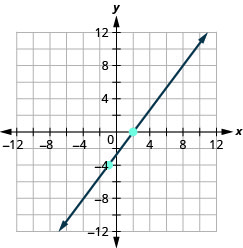
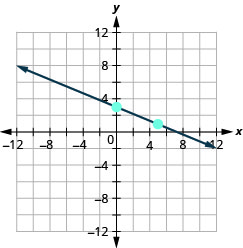
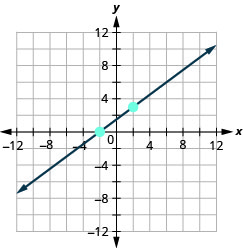
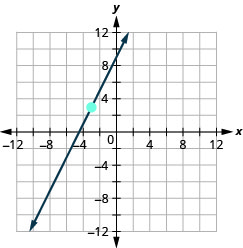
En los siguientes ejercicios, encuentra la pendiente de cada línea mostrada.
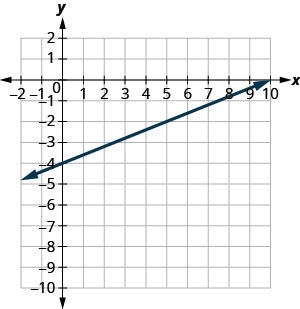
- Responder
-
\(\frac{2}{5}\)
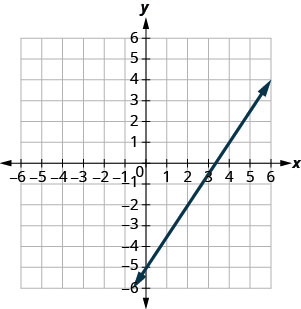
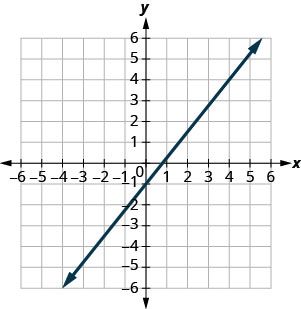
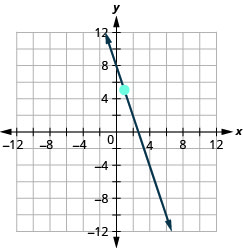
- Responder
-
\(\frac{5}{4}\)
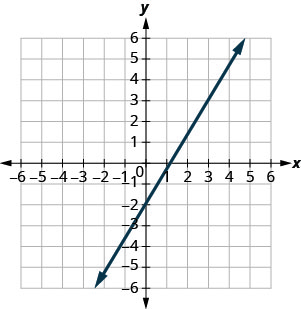
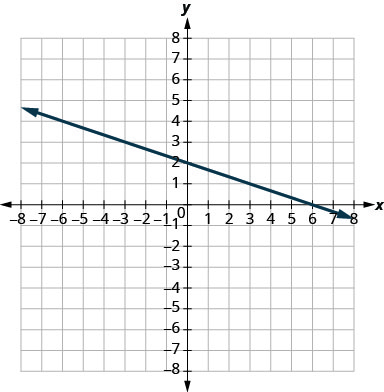
- Responder
-
\(-\frac{1}{3}\)
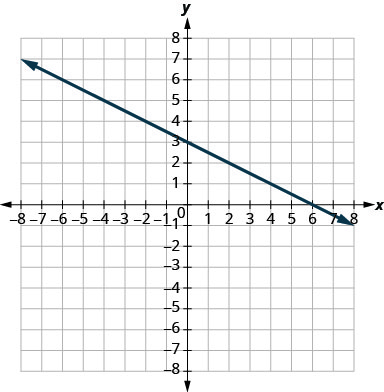
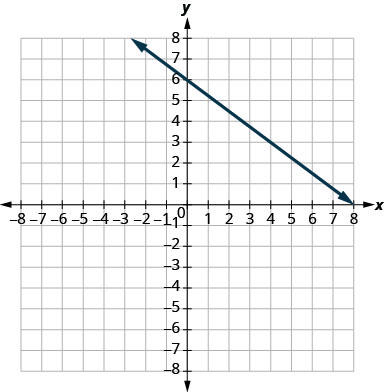
- Responder
-
\(-\frac{3}{4}\)
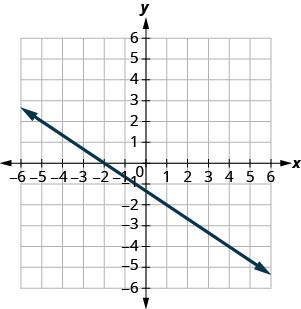
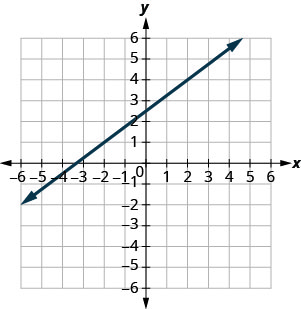
- Responder
-
\(\frac{3}{4}\)
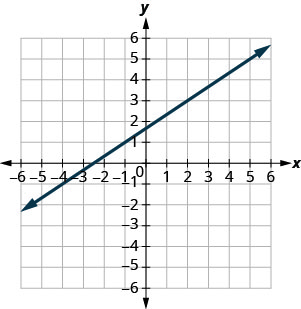
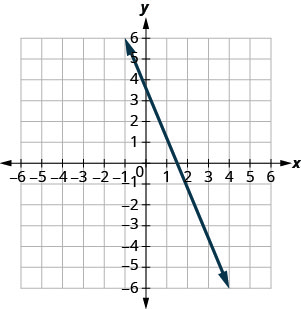
- Responder
-
\(-\frac{5}{2}\)
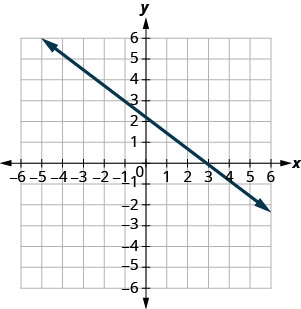
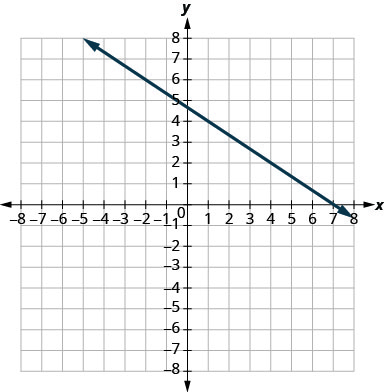
- Responder
-
\(-\frac{2}{3}\)
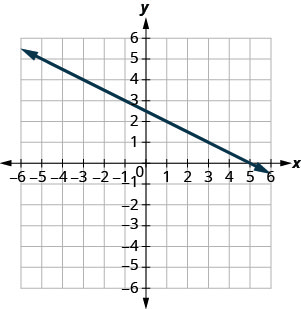
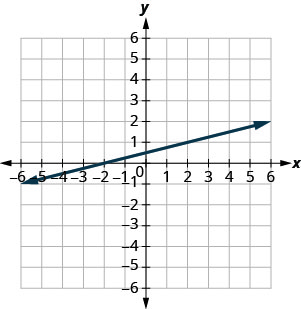
- Responder
-
\(\frac{1}{4}\)
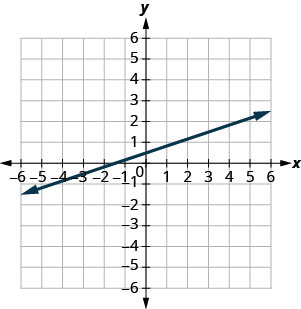
Encuentra la Pendiente de Líneas Horizontales y Verticales
En los siguientes ejercicios, encuentra la pendiente de cada línea.
y=3
- Responder
-
0
y=1
x=4
- Responder
-
undefined
x=2
y=−2
- Responder
-
0
y=−3
x=−5
- Responder
-
undefined
x=−4
Usa la Fórmula de Talud para encontrar la Talud de una Línea entre Dos Puntos
En los siguientes ejercicios, usa la fórmula de pendiente para encontrar la pendiente de la línea entre cada par de puntos.
(1,4), (3,9)
- Responder
-
\(\frac{5}{2}\)
(2,3), (5,7)
(0,3), (4,6)
- Contestar
-
\(\frac{3}{4}\)
(0,1), (5,4)
(2,5), (4,0)
- Contestar
-
\(-\frac{5}{2}\)
(3,6), (8,0)
(−3,3), (4, −5)
- Contestar
-
\(-\frac{8}{7}\)
(−2,4), (3, −1)
(−1, −2), (2,5)
- Contestar
-
\(\frac{7}{3}\)
(−2, −1), (6,5)
(4, −5), (1, −2)
- Contestar
-
−1
(3, −6), (2, −2)
Graficar una línea dado un punto y el talud
En los siguientes ejercicios, grafica cada línea con el punto y pendiente dados.
\((1,-2) ; m=\frac{3}{4}\)
- Contestar
-
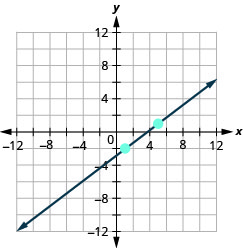
\((1,-1) ; m=\frac{2}{3}\)
\((2,5) ; m=-\frac{1}{3}\)
- Contestar
-
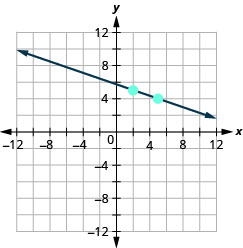
\((1,4) ; m=-\frac{1}{2}\)
\((-3,4) ; m=-\frac{3}{2}\)
- Contestar
-
\((-2,5) ; m=-\frac{5}{4}\)
\((-1,-4) ; m=\frac{4}{3}\)
- Contestar
-
\((-3,-5) ; m=\frac{3}{2}\)
\(y\)-interceptar\(3 ; m=-\frac{2}{5}\)
- Contestar
-
\(y\)-interceptar\(5 ; m=-\frac{4}{3}\)
\(x\)-interceptar\(-2 ; m=\frac{3}{4}\)
- Contestar
-
\(x\)-interceptar\(-1 ; m=\frac{1}{5}\)
\((-3,3) ; m=2\)
- Contestar
-
\((-4,2) ; m=4\)
\((1,5) ; m=-3\)
- Contestar
-
\((2,3) ; m=-1\)
Matemáticas cotidianas
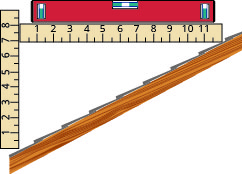
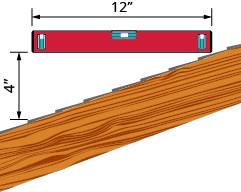
Pendiente de una cubierta. Una manera fácil de determinar la pendiente de un techo es establecer un extremo de un nivel de 12 pulgadas en la superficie del techo y sostenerlo nivelado. Luego toma una cinta métrica o regla y mide desde el otro extremo del nivel hasta la superficie del techo. Esto te dará la pendiente de la cubierta. Los constructores, a veces, se refieren a esto como pitch y lo afirman como un significado de “x 12 pitch”\(\frac{x}{12}\), donde x es la medida desde el techo hasta el nivel: la subida. También a veces se afirma como un “tono x-in-12".
- ¿Cuál es la pendiente de la cubierta en esta imagen?
- ¿Cuál es el tono en términos de construcción?
- Contestar
-
- \(\frac{1}{3}\)
- 4 12 pitch o 4-en-12 pitch
La pendiente de la cubierta que se muestra aquí se mide con un nivel de 12” y una regla. ¿Cuál es la pendiente de este techo?
Grado vial. Una carretera local tiene una pendiente de 6%. El grado de una carretera es su pendiente expresada como porcentaje. Encuentra la pendiente de la carretera como una fracción y luego simplifica. ¿Qué subida y carrera reflejaría esta pendiente o pendiente?
- Contestar
-
\(\frac{3}{50} ;\)subida\(=3,\) correr\(=50\)
Grado de carretera. Una carretera local se eleva 2 pies por cada 50 pies de carretera.
- ¿Cuál es la pendiente de la autopista?
- El grado de una carretera es su pendiente expresada como porcentaje. ¿Cuál es el grado de esta autopista?
Rampa para sillas de ruedas Las reglas para rampas para sillas de ruedas requieren un aumento máximo de 1 pulgada para una carrera de 12 pulgadas.
- ¿Cuánto tiempo debe durar la rampa para dar cabida a una elevación de 24 pulgadas a la puerta?
- Crea un modelo de esta rampa.
- Contestar
-
- 288 pulgadas (24 pies)
- Los modelos variarán.
Rampa para sillas de ruedas Una elevación de 1 pulgada para una carrera de 16 pulgadas facilita que el conductor de silla de ruedas ascienda por una rampa.
- ¿Cuánto tiempo debe ser una rampa para acomodar fácilmente una elevación de 24 pulgadas a la puerta?
- Crea un modelo de esta rampa.
Ejercicios de escritura
¿Qué te dice el letrero de la pendiente de una línea?
- Contestar
-
Cuando la pendiente es un número positivo la línea sube de izquierda a derecha. Cuando la pendiente es un número negativo la línea baja de izquierda a derecha.
¿En qué se\(m=\frac{1}{2}\) diferencia la gráfica de una línea con pendiente de la gráfica de una línea con pendiente?\(m=2 ?\)
¿Por qué la pendiente de una línea vertical es “indefinida”?
- Contestar
-
Una línea vertical tiene 0 corridas y como la división por 0 no está definida la pendiente es indefinida.
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
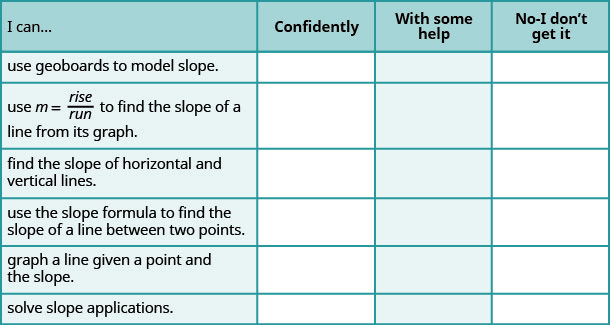
ⓑ En una escala del 1—10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?
Glosario
- geobordo
- Un geoboard es un tablero con una rejilla de clavijas en él.
- pendiente negativa
- Una pendiente negativa de una línea baja a medida que lee de izquierda a derecha.
- pendiente positiva
- Una pendiente positiva de una línea sube a medida que lees de izquierda a derecha.
- subir
- El ascenso de una línea es su cambio vertical.
- correr
- El recorrido de una línea es su cambio horizontal.
- fórmula de pendiente
- La pendiente de la línea entre dos puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\) es\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\).
- pendiente de una línea
- La pendiente de una línea es\(m=\frac{\text { rise }}{\text { run }}\). La subida mide el cambio vertical y la corrida mide el cambio horizontal.