4.6: Encontrar la ecuación de una línea
- Page ID
- 110234
Al final de esta sección, podrás:
- Encontrar una ecuación de la línea dada la pendiente y la intercepción y
- Encontrar una ecuación de la línea dada la pendiente y un punto
- Encuentra una ecuación de la línea dada dos puntos
- Encontrar una ecuación de una línea paralela a una línea dada
- Encontrar una ecuación de una línea perpendicular a una línea dada
Antes de comenzar, toma este cuestionario de preparación.
- Resolver:\(\frac{2}{3} = \frac{x}{5}\).
Si te perdiste este problema, revisa el Ejercicio 2.2.4. - Simplificar:\(−\frac{2}{5}(x−15)\).
Si te perdiste este problema, revisa el Ejercicio 1.10.34.
¿Cómo saben los minoristas en línea que 'también le puede gustar' un artículo en particular basado en algo que acaba de pedir? ¿Cómo pueden saber los economistas cómo un aumento en el salario mínimo afectará la tasa de desempleo? ¿Cómo crean los investigadores médicos medicamentos para apuntar a las células cancerosas? ¿Cómo pueden los ingenieros de tránsito predecir el efecto en su tiempo de viaje de un aumento o disminución en los precios de la gasolina? Todo son matemáticas.
Estás en un punto emocionante de tu viaje matemático ya que las matemáticas que estás estudiando tienen aplicaciones interesantes en el mundo real.
Las ciencias físicas, las ciencias sociales y el mundo empresarial están llenas de situaciones que pueden modelarse con ecuaciones lineales que relacionan dos variables. Los datos son recolectados y graficados. Si los puntos de datos parecen formar una línea recta, se puede usar una ecuación de esa línea para predecir el valor de una variable en función del valor de la otra variable.
Para crear un modelo matemático de una relación lineal entre dos variables, debemos ser capaces de encontrar la ecuación de la línea. En esta sección veremos varias formas de escribir la ecuación de una línea. El método específico que usemos estará determinado por la información que se nos proporcione.
Encontrar una ecuación de la línea dada la pendiente y -Intercepción
Podemos determinar fácilmente la pendiente e intercepción de una línea si la ecuación fue escrita en forma pendiente-interceptar, y=mx+b Ahora, haremos lo contrario, comenzaremos con la pendiente y -interceptar y las usaremos para encontrar la ecuación de la línea.
Encuentra una ecuación de una línea con pendiente −7 e intercepción y (0, −1).
- Contestar
-
Dado que se nos da la pendiente y -intercepción de la línea, podemos sustituir los valores necesarios en la forma pendiente-intercepción, y=mx+b.
Nombra la pendiente. 
Nombra la intercepción y. 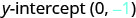
Sustituir los valores en y=mx+b. 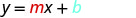
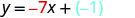
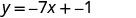
Encuentra una ecuación de una línea con pendiente\(\frac{2}{5}\) e intercepción y (0,4).
- Contestar
-
\(y = \frac{2}{5}x + 4\)
Encuentra una ecuación de una línea con pendiente −1 e intercepción y (0, −3).
- Contestar
-
\(y=−x−3\)
En ocasiones, la pendiente y la intercepción deben determinarse a partir de la gráfica.
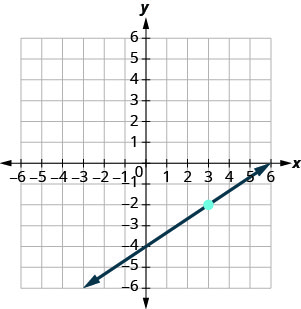
Encuentra la ecuación de la línea que se muestra.
- Contestar
-
Necesitamos encontrar la pendiente y -intercepción de la línea de la gráfica para poder sustituir los valores necesarios en la forma pendiente-intercepción, y=mx+por=mx+b.
Para encontrar la pendiente, elegimos dos puntos en la gráfica.
La intercepción y es (0, −4) y la gráfica pasa a través de (3, −2).
Encuentra la pendiente contando la subida y la carrera. 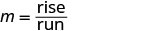

Encuentra la intercepción y. 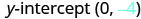
Sustituir los valores en y=mx+b. 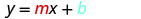
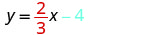
Encuentra la ecuación de la línea que se muestra en la gráfica.
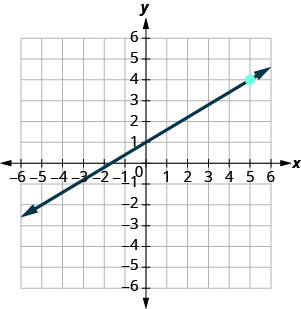
- Contestar
-
\(y=\frac{3}{5}x+1\)
Encuentra la ecuación de la línea que se muestra en la gráfica.
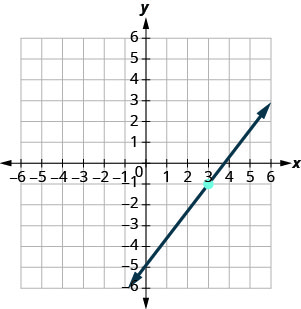
- Contestar
-
\(y=\frac{4}{3}x−5\)
Encontrar una ecuación de la línea dada la pendiente y un punto
Encontrar una ecuación de una línea usando la forma pendiente-intercepción de la ecuación funciona bien cuando se le da la pendiente y -intercepción o cuando las lee de una gráfica. Pero, ¿qué pasa cuando tienes otro punto en lugar de la intercepción y?
Vamos a utilizar la fórmula de pendiente para derivar otra forma de una ecuación de la línea. Supongamos que tenemos una línea que tiene pendiente mm y que contiene algún punto específico\((x_{1}, y_{1})\) y algún otro punto, al que simplemente llamaremos (x, y). Podemos escribir la pendiente de esta línea y luego cambiarla a una forma diferente.
\(\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x−x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the y terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)
Este formato se llama la forma punto-pendiente de una ecuación de una línea.
La forma punto-pendiente de una ecuación de una línea con pendiente mm y que contiene el punto\((x_{1}, y_{1})\) es
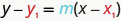
Podemos usar la forma punto-pendiente de una ecuación para encontrar una ecuación de una línea cuando se nos da la pendiente y un punto. Luego reescribiremos la ecuación en forma pendiente-intercepción. La mayoría de las aplicaciones de ecuaciones lineales utilizan la forma pendiente-intercepción.
Encuentra una ecuación de una línea con pendiente\(m=\frac{2}{5}\) que contenga el punto (10,3). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-




Encuentra una ecuación de una línea con pendiente\(m=\frac{5}{6}\) y que contenga el punto (6,3).
- Contestar
-
\(y=\frac{5}{6}x−2\)
Encuentra una ecuación de una línea con pendiente\(m=\frac{2}{3}\) y que contenga el punto (9,2).
- Contestar
-
\(y=\frac{2}{3}x−4\)
- Identificar la pendiente.
- Identificar el punto.
- Sustituir los valores en la forma de punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
Encuentra una ecuación de una línea con pendiente\(m=−\frac{1}{3}\) que contenga el punto (6, −4). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
Dado que se nos da un punto y la pendiente de la línea, podemos sustituir los valores necesarios en la forma punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
Identificar la pendiente. 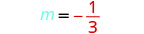
Identificar el punto. 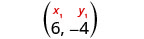
Sustituir los valores en\(y−y_{1}=m(x−x_{1})\). 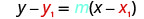
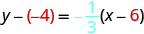
Simplificar. 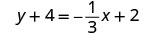
Escribir en forma de pendiente—interceptar. 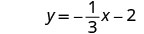
Encuentra una ecuación de una línea con pendiente\(m=−\frac{2}{5}\) y que contenga el punto (10, −5).
- Contestar
-
\(y=−\frac{2}{5}x−1\)
Encuentre una ecuación de una línea con pendiente\(m=−\frac{3}{4}\), y que contenga el punto (4, −7).
- Contestar
-
\(y=−\frac{3}{4}x−4\)
Encuentra una ecuación de una línea horizontal que contenga el punto (−1,2). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
Cada línea horizontal tiene pendiente 0. Podemos sustituir la pendiente y los puntos en la forma punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
¿Terminamos con la forma de una línea horizontal, y=a?Identificar la pendiente. 
Identificar el punto. 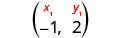
Sustituir los valores en\(y−y_{1}=m(x−x_{1})\). 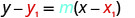
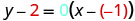
Simplificar. 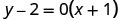
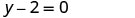
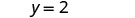
Escribir en forma de pendiente—interceptar. Está en forma y, pero podría escribirse y=0x+2.
Encuentra una ecuación de una línea horizontal que contenga el punto (−3,8).
- Contestar
-
y = 8
Encuentra una ecuación de una línea horizontal que contenga el punto (−1,4).
- Contestar
-
y = 4
Encontrar una ecuación de la línea dada dos puntos
Cuando se recopilan datos del mundo real, se puede crear un modelo lineal a partir de dos puntos de datos. En el siguiente ejemplo veremos cómo encontrar una ecuación de una línea cuando se dan solo dos puntos.
Tenemos dos opciones hasta el momento para encontrar una ecuación de una línea: pendiente-intercepción o punto-pendiente. Como conoceremos dos puntos, tendrá más sentido usar la forma punto-pendiente.
Pero entonces necesitamos la pendiente. ¿Podemos encontrar la pendiente con sólo dos puntos? Sí. Entonces, una vez que tengamos la pendiente, podemos usarla y uno de los puntos dados para encontrar la ecuación.
Encuentra una ecuación de una línea que contenga los puntos (5,4) y (3,6). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-




Usa el punto (3,6) y ve que obtienes la misma ecuación.
Encuentra una ecuación de una línea que contenga los puntos (3,1) y (5,6).
- Contestar
-
\(y=\frac{5}{2}x−\frac{13}{2}\)
Encuentra una ecuación de una línea que contenga los puntos (1,4) y (6,2).
- Contestar
-
\(y=−\frac{2}{5}x+\frac{22}{5}\)
- Encuentra la pendiente usando los puntos dados.
- Elige un punto.
- Sustituir los valores en la forma de punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
Encuentre una ecuación de una línea que contenga los puntos (−3, −1) y (2, −2). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
Como tenemos dos puntos, encontraremos una ecuación de la línea usando la forma punto-pendiente. El primer paso será encontrar la pendiente.
Encuentra la pendiente de la línea a través de (−3, −1) y (2, −2). 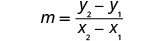
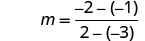
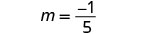
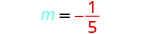
Elija cualquiera de los dos puntos. 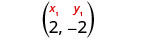
Sustituir los valores en\(y−y_{1}=m(x−x_{1})\). 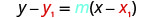
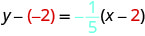
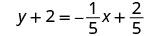
Escribir en forma de pendiente—interceptar. 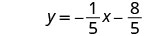
Encuentra una ecuación de una línea que contenga los puntos (−2, −4) y (1, −3).
- Contestar
-
\(y=\frac{1}{3}x−\frac{10}{3}\)
Encuentra una ecuación de una línea que contenga los puntos (−4, −3) y (1, −5).
- Contestar
-
\(y=−\frac{2}{5}x−\frac{23}{5}\)
Encuentre una ecuación de una línea que contenga los puntos (−2,4) y (−2, −3). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
Nuevamente, el primer paso será encontrar la pendiente.
\(\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}\)
Esto nos dice que es una línea vertical. Ambos puntos tienen una coordenada x de −2. Entonces nuestra ecuación de la línea es x=−2. Como no hay yy, no podemos escribirlo en forma pendiente-interceptar.
Es posible que desee esbozar una gráfica usando los dos puntos dados. ¿La gráfica concuerda con nuestra conclusión de que se trata de una línea vertical?
Encuentra una ecuación de una línea que contenga los puntos (5,1) y (5, −4).
- Contestar
-
x = 5
Encuentra una ecuación de una línea que contenga los puntos (−4,4) y (−4,3).
- Contestar
-
x=−4
Hemos visto que podemos usar la forma pendiente-intercepción o la forma punto-pendiente para encontrar una ecuación de una línea. El formulario que utilicemos dependerá de la información que nos den. Esto se resume en la Tabla\(\PageIndex{1}\).
| Para escribir una ecuación de una línea | ||
| Si se da: | Uso: | Forma: |
| Pendiente e intercepción y | pendiente—intercepción | y=mx+b |
| Talud y un punto | punto-pendiente | \(y−y_{1}=m(x−x_{1})\) |
| Dos puntos | punto-pendiente | \(y−y_{1}=m(x−x_{1})\) |
Encontrar una ecuación de una línea paralela a una línea dada
Supongamos que necesitamos encontrar una ecuación de una línea que pase por un punto específico y sea paralela a una línea dada. Podemos aprovechar el hecho de que las líneas paralelas tienen la misma pendiente. Entonces tendremos un punto y la pendiente, justo lo que necesitamos para usar la ecuación punto-pendiente.
Primero veamos esto gráficamente.
La gráfica muestra la gráfica de y=2x−3. Queremos graficar una línea paralela a esta línea y que pase por el punto (−2,1).
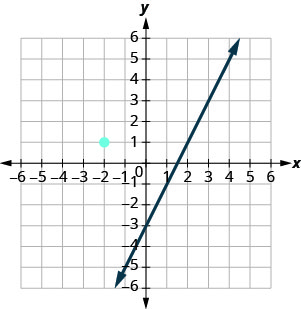
Sabemos que las líneas paralelas tienen la misma pendiente. Entonces la segunda línea tendrá la misma pendiente que y=2x−3. Esa pendiente es\(m_{\|} = 2\). Usaremos la notación\(m_{\|}\) para representar la pendiente de una línea paralela a una línea con pendiente m. (Observe que el subíndice se parece a dos líneas paralelas).
La segunda línea pasará por (−2,1) y tendrá m=2. Para graficar la línea, partimos en (−2,1) y contamos la subida y la carrera. Con m=2 (o\(m=\frac{2}{1}\)), contamos la subida 2 y la carrera 1. Dibujamos la línea.
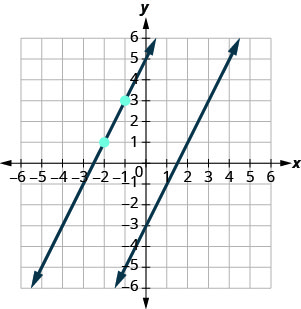
¿Las líneas aparecen paralelas? ¿La segunda línea pasa a través de (−2,1)?
Ahora, veamos cómo hacer esto algebraicamente.
Podemos usar la forma pendiente-interceptar o la forma punto-pendiente para encontrar una ecuación de una línea. Aquí conocemos un punto y podemos encontrar la pendiente. Entonces usaremos la forma punto-pendiente.
Encuentra una ecuación de una línea paralela a y=2x−3 que contiene el punto (−2,1). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
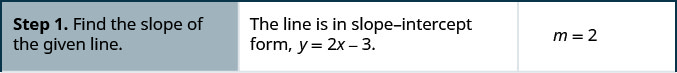




¿Tiene sentido esta ecuación? ¿Cuál es la intercepción y de la línea? ¿Cuál es la pendiente?
Encuentra una ecuación de una línea paralela a la línea y=3x+1 que contiene el punto (4,2). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
y=3x−10
Encuentra una ecuación de una línea paralela a la línea\(y=\frac{1}{2}x−3\) que contiene el punto (6,4).
- Contestar
-
\(y=\frac{1}{2}x+1\)
- Encuentra la pendiente de la línea dada.
- Encuentra la pendiente de la línea paralela.
- Identificar el punto.
- Sustituya los valores en la forma punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
Encontrar una ecuación de una línea perpendicular a una línea dada
Ahora, consideremos líneas perpendiculares. Supongamos que necesitamos encontrar una línea que pase por un punto específico y que sea perpendicular a una línea dada. Podemos aprovechar el hecho de que las líneas perpendiculares tienen pendientes que son recíprocas negativas. Volveremos a usar la ecuación punto-pendiente, como hicimos con líneas paralelas.
La gráfica muestra la gráfica de y=2x−3. Ahora, queremos graficar una línea perpendicular a esta línea y que pasa por (−2,1).

Sabemos que las líneas perpendiculares tienen pendientes que son recíprocas negativas. Usaremos la notación\(m_{\perp}\) para representar la pendiente de una línea perpendicular a una línea con pendiente m. (Observe que el subíndice\(_{\perp}\) se parece a los ángulos rectos hechos por dos líneas perpendiculares.)
\[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\]
Ahora sabemos que la línea perpendicular pasará por (−2,1) con\(m_{\perp}=−\frac{1}{2}\).
Para graficar la línea, comenzaremos en (−2,1) y contaremos la subida −1 y la carrera 2. Después trazamos la línea.
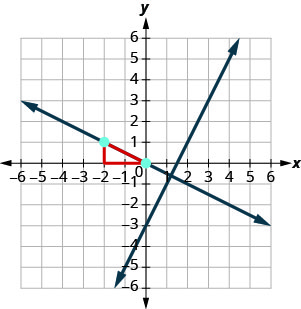
¿Las líneas aparecen perpendiculares? ¿La segunda línea pasa a través de (−2,1)?
Ahora, veamos cómo hacer esto algebraicamente. Podemos usar la forma pendiente-interceptar o la forma punto-pendiente para encontrar una ecuación de una línea. En este ejemplo conocemos un punto, y podemos encontrar la pendiente, por lo que usaremos la forma punto-pendiente.
Encuentra una ecuación de una línea perpendicular a y=2x−3 que contiene el punto (−2,1). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-





Encuentra una ecuación de una línea perpendicular a la línea y=3x+1 que contiene el punto (4,2). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
\(y=−\frac{1}{3}x+\frac{10}{3}\)
Encuentra una ecuación de una línea perpendicular a la línea\(y=\frac{1}{2}x−3\) que contiene el punto (6,4).
- Contestar
-
y=−2x+16
- Encuentra la pendiente de la línea dada.
- Encuentra la pendiente de la línea perpendicular.
- Identificar el punto.
- Sustituya los valores en la forma punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
Encuentra una ecuación de una línea perpendicular a x=5 que contiene el punto (3, −2). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
Nuevamente, como conocemos un punto, la opción punto-pendiente parece más prometedora que la opción pendiente-interceptar. Necesitamos la pendiente para usar esta forma, y sabemos que la nueva línea será perpendicular a x=5. Esta línea es vertical, por lo que su perpendicular será horizontal. Esto nos dice el\(m_{\perp}=0\).
\(\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}\)
Dibuje la gráfica de ambas líneas. ¿Parecen ser perpendiculares?
Encuentra una ecuación de una línea que es perpendicular a la línea x=4 que contiene el punto (4, −5). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
y=−5
Encuentra una ecuación de una línea que es perpendicular a la línea x=2 que contiene el punto (2, −1). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
y=−1
En Ejercicio\(\PageIndex{31}\), usamos la forma punto-pendiente para encontrar la ecuación. Podríamos haber mirado esto de otra manera.
Queremos encontrar una línea que sea perpendicular a x=5 que contenga el punto (3, −2). La gráfica nos muestra la línea x=5 y el punto (3, −2).
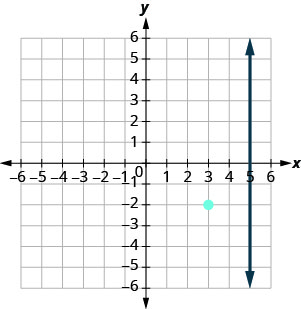
Sabemos que cada línea perpendicular a una línea vertical es horizontal, por lo que esbozaremos la línea horizontal a través de (3, −2).
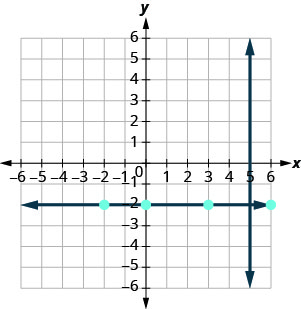
¿Las líneas aparecen perpendiculares?
Si miramos algunos puntos en esta línea horizontal, notamos que todos tienen coordenadas y de −2. Entonces, la ecuación de la línea perpendicular a la línea vertical x=5 es y=−2.
Encuentra una ecuación de una línea que es perpendicular a y=−4 que contiene el punto (−4,2). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
La línea y=−4 es una línea horizontal. Cualquier línea perpendicular a ella debe ser vertical, en la forma x=a.Dado que la línea perpendicular es vertical y pasa a través de (−4,2), cada punto en ella tiene una coordenada x de −4. La ecuación de la línea perpendicular es x=−4. Es posible que desee esbozar las líneas. ¿Aparecen perpendiculares?
Encuentra una ecuación de una línea que es perpendicular a la línea y=1 que contiene el punto (−5,1). Escribe la ecuación en forma de pendiente-intercepción.
- Contestar
-
x=−5
Encuentra una ecuación de una línea que es perpendicular a la línea y=−5 que contiene el punto (−4, −5).
- Contestar
-
x=−4
Acceda a este recurso en línea para obtener instrucción adicional y práctica con la búsqueda de la ecuación de una línea.
Conceptos clave
- Para encontrar una ecuación de una línea dada la pendiente y un punto
- Identificar la pendiente.
- Identificar el punto.
- Sustituir los valores en la forma de punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
- Para encontrar una ecuación de una línea dada dos puntos
- Encuentra la pendiente usando los puntos dados.
- Elige un punto.
- Sustituir los valores en la forma de punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
- Escribir y Ecuación de una Línea
- Si se le da pendiente e\(y\) intercepción, utilice la forma pendiente-intercepción\(y=mx+b\).
- Si se le da pendiente y un punto, utilice la forma punto-pendiente\(y−y_{1}=m(x−x_{1})\).
- Si se le dan dos puntos, utilice la forma punto-pendiente\(y−y_{1}=m(x−x_{1})\).
- Para encontrar una ecuación de una línea paralela a una línea dada
- Encuentra la pendiente de la línea dada.
- Encuentra la pendiente de la línea paralela.
- Identificar el punto.
- Sustituir los valores en la forma de punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
- Para encontrar una ecuación de una línea perpendicular a una línea dada
- Encuentra la pendiente de la línea dada.
- Encuentra la pendiente de la línea perpendicular.
- Identificar el punto.
- Sustituir los valores en la forma de punto-pendiente,\(y−y_{1}=m(x−x_{1})\).
- Escribe la ecuación en forma de pendiente-intercepción.
Glosario
- forma punto-pendiente
- La forma punto-pendiente de una ecuación de una línea con pendiente mm y que contiene el punto\(\left(x_{1}, y_{1}\right)\) es\(y-y_{1}=m\left(x-x_{1}\right)\).


