4.5E: Ejercicios
( \newcommand{\kernel}{\mathrm{null}\,}\)
La práctica hace la perfección
Reconocer la relación entre la gráfica y la forma pendiente-intercepción de una ecuación de una línea
En los siguientes ejercicios, usa la gráfica para encontrar la pendiente ey -intercepción de cada línea. Compara los valores con la ecuacióny=mx+b.
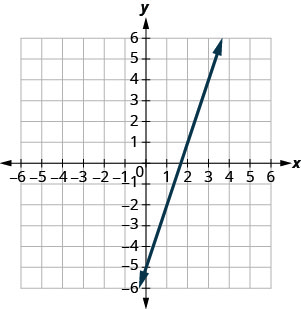
y=3x−5
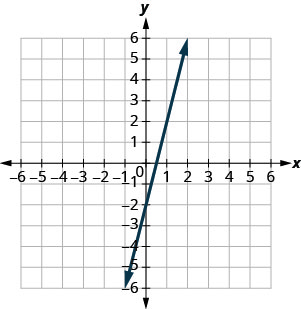
y=4x−2
- Contestar
-
pendientem=4 ey intercepción(0,−2)
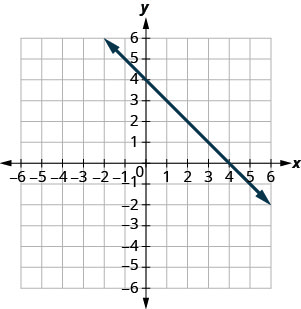
y=−x+4
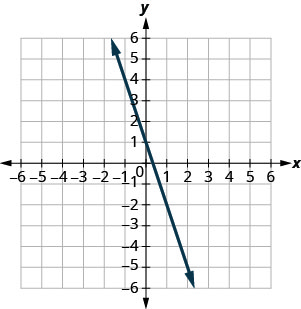
y=−3x+1
- Contestar
-
pendientem=−3 ey intercepción(0,1)
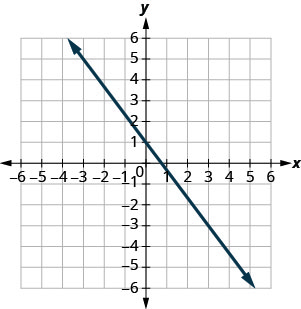
y=−43x+1
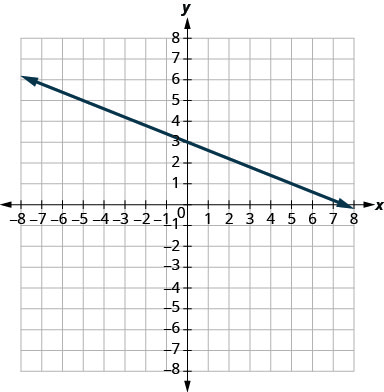
y=−25x+3
- Contestar
-
pendientem=−25 ey intercepción(0,3)
Identificar el talud ey -interceptar a partir de una ecuación de una línea
En los siguientes ejercicios, identificar la pendiente ey -intercepción de cada línea.
y=−7x+3
y=−9x+7
- Contestar
-
m=−9;y -interceptar:(0,7)
y=6x−8
y=4x−10
- Contestar
-
m=4;y -interceptar:(0,−10)
3x+y=5
4x+y=8
- Contestar
-
m=−4\0;\(y-interceptar:(0,8)
6x+4y=12
8x+3y=12
- Contestar
-
m=−83;y -interceptar:(0,4)
5x−2y=6
7x−3y=9
- Contestar
-
m=73;y -interceptar:(0,−3)
Graficar una línea usando su pendiente e intercepción
En los siguientes ejercicios, grafica la línea de cada ecuación usando su pendiente ey -intercepción.
y=x+3
y=x+4
- Contestar
-
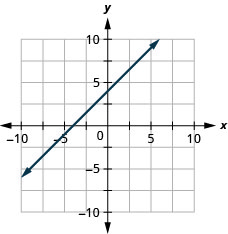
y=3x−1
y=2x−3
- Contestar
-
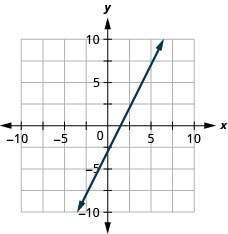
y=−x+2
y=−x+3
- Contestar
-
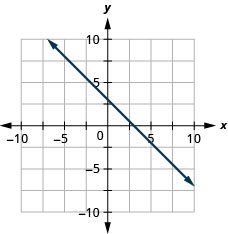
y=−x−4
y=−x−2
- Contestar
-
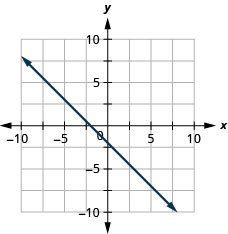
y=−34x−1
y=−25x−3
- Contestar
-
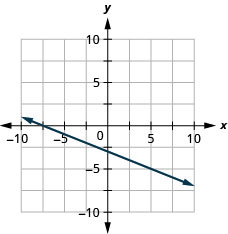
y=−35x+2
y=−23x+1
- Contestar
-
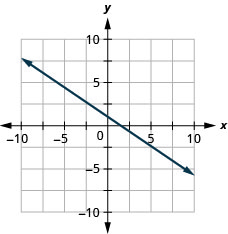
3x−4y=8
4x−3y=6
- Contestar
-
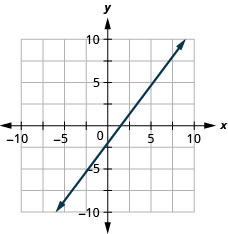
y=0.1x+15
y=0.3x+25
- Contestar
-
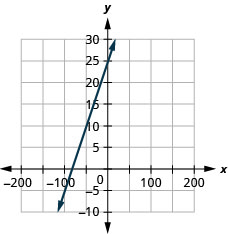
Elija el método más conveniente para graficar una línea
En los siguientes ejercicios, determine el método más conveniente para graficar cada línea.
x=2
y=4
- Contestar
-
línea horizontal
y=5
x=−3
- Contestar
-
línea vertical
y=−3x+4
y=−5x+2
- Contestar
-
pendiente—intercepción
x−y=5
x−y=1
- Contestar
-
intercepta
y=23x−1
y=45x−3
- Contestar
-
pendiente—intercepción
y=−3
y=−1
- Contestar
-
línea horizontal
3x−2y=−12
2x−5y=−10
- Contestar
-
intercepta
y=−14x+3
y=−13x+5
- Contestar
-
pendiente—intercepción
Graficar e interpretar aplicaciones de pendiente—Interceptar
La ecuaciónP=31+1.75w modela la relación entre el monto del pago mensual de la factura de agua de TuyetP, en dólares, y el número de unidades de agua,w, utilizadas.
- Encuentra el pago de Tuyet por un mes cuando se utilizan0 unidades de agua.
- Encuentra el pago de Tuyet por un mes cuando se utilizan12 unidades de agua.
- Interpretar la pendiente eP -intercepción de la ecuación.
- Grafica la ecuación.
La ecuaciónP=28+2.54w modela la relación entre el monto del pago mensual de la factura de agua de RandyP, en dólares, y el número de unidades de agua,w, utilizadas.
- Encuentra el pago de un mes cuando Randy utilizó0 unidades de agua.
- Encuentra el pago de un mes cuando Randy utilizó15 unidades de agua.
- Interpretar la pendiente eP -intercepción de la ecuación.
- Grafica la ecuación.
- Contestar
-
- $28
- $66.10
- La pendiente,2.54, significa que el pago de RandyP,, aumenta$2.54 cuando el número de unidades de agua que utilizó,w, narruga por1. ElP -intercepto significa que si el número de unidades de agua que utilizó Randy era0, el pago sería$28.
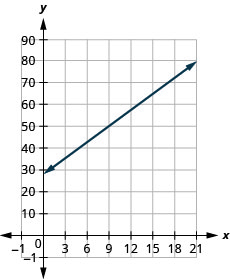
Bruce conduce su auto para su trabajo. La ecuaciónR=0.575m+42 modela la relación entre el monto en dólaresR,, que se le reembolsa y el número de millasm,, conduce en un día.
- Encuentra la cantidad a Bruce que se le reembolsa en un día en el que conduce0 millas.
- Encuentra la cantidad a Bruce que se le reembolsa en un día en el que conduce220 millas.
- Interpretar la pendiente eR -intercepción de la ecuación.
- Grafica la ecuación.
Janelle planea rentar un auto mientras está de vacaciones. La ecuaciónC=0.32m+15 modela la relación entre el costo en dólaresC,, por día y el número de millas,m, ella conduce en un día.
- Encuentra el costo si Janelle conduce el auto0 millas un día.
- Encuentra el costo en un día en que Janelle conduce400 millas del auto.
- Interpretar la pendiente eC -intercepción de la ecuación.
- Grafica la ecuación.
- Contestar
-
- $15
- $143
- La pendiente,0.32, significa que el costo,C, aumenta$0.32 cuando el número de millas conducidas,m, aumenta en1. ElC -intercepto significa que si Janelle conduce0 millas algún día, el costo sería$15.
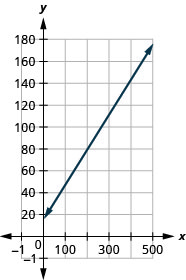
Cherie trabaja en retail y su salario semanal incluye comisión por la cantidad que vende. La ecuaciónS=400+0.15c modela la relación entre su salario semanalS,, en dólares y el monto de sus ventas,c, en dólares.
- Encuentra el salario de Cherie para una semana cuando sus ventas fueron0.
- Encuentra el salario de Cherie para una semana cuando sus ventas fueron3600.
- Interpretar la pendiente eS -intercepción de la ecuación.
- Grafica la ecuación.
El salario semanal de Patel incluye un sueldo base más una comisión por sus ventas. La ecuaciónS=750+0.09c modela la relación entre su salario semanalS,, en dólares y el monto de sus ventas,c, en dólares.
- Encuentra el salario de Patel para una semana cuando sus ventas fueron0.
- Encuentra el salario de Patel para una semana cuando sus ventas fueron18,540.
- Interpretar la pendiente eS -intercepción de la ecuación.
- Grafica la ecuación.
- Contestar
-
- $750
- $2418.60
- El desnivel0.09,, significa que el salario de PatelS,, aumenta$0.09 por cada$1 incremento en sus ventas. ElS -intercepto significa que cuando sus ventas son$0, su salario lo es$750.
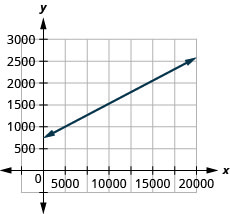
Costa está planeando un banquete de almuerzo. La ecuaciónC=450+28g modela la relación entre el costo en dólares,C, del banquete y el número de invitados,g.
- Encuentra el costo si el número de invitados es40.
- Encuentra el costo si el número de invitados es80.
- Interpretar la pendiente eC -intercepción de la ecuación.
- Grafica la ecuación.
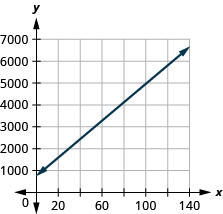
Margie está planeando una cena banquete. La ecuaciónC=750+42g modela la relación entre el costo en dólares,C, del banquete y el número de invitados,g.
- Encuentra el costo si el número de invitados es50.
- Encuentra el costo si el número de invitados es100.
- Interpretar la pendiente eC -intercepción de la ecuación.
- Grafica la ecuación.
- Contestar
-
- $2850
- $4950
- La pendiente,42, significa que el costo,C, aumenta por$42 para cuando el número de invitados aumenta en1. ElC -intercepto significa que cuando el número de invitados es0, el costo sería$750.
Uso de pendientes para identificar líneas paralelas
En los siguientes ejercicios, utilice pendientes ey intercepciones para determinar si las líneas son paralelas.
y=34x−3;3x−4y=−2
y=23x−1;2x−3y=−2
- Contestar
-
paralelo
2x−5y=−3;y=25x+1
3x−4y=−2;y=34x−3
- Contestar
-
paralelo
2x−4y=6;x−2y=3
6x−3y=9;2x−y=3
- Contestar
-
no paralelo
4x+2y=6;6x+3y=3
8x+6y=6;12x+9y=12
- Contestar
-
paralelo
x=5;x=−6
x=7;x=−8
- Contestar
-
paralelo
x=−4;x=−1
x=−3;x=−2
- Contestar
-
paralelo
y=2;y=6
y=5;y=1
- Contestar
-
paralelo
y=−4;y=3
y=−1;y=2
- Contestar
-
paralelo
x−y=2;2x−2y=4
4x+4y=8;x+y=2
- Contestar
-
no paralelo
x−3y=6;2x−6y=12
5x−2y=11;5x−y=7
- Contestar
-
no paralelo
3x−6y=12;6x−3y=3
4x−8y=16;x−2y=4
- Contestar
-
no paralelo
9x−3y=6;3x−y=2
x−5y=10;5x−y=−10
- Contestar
-
no paralelo
7x−4y=8;4x+7y=14
9x−5y=4;5x+9y=−1
- Responder
-
no paralelo
Uso de pendientes para identificar líneas perpendiculares
En los siguientes ejercicios, utilice pendientes ey intercepciones para determinar si las líneas son perpendiculares.
3x−2y=8;2x+3y=6
x−4y=8;4x+y=2
- Responder
-
perpendicular
2x+5y=3;5x−2y=6
2x+3y=5;3x−2y=7
- Responder
-
perpendicular
3x−2y=1;2x−3y=2
3x−4y=8;4x−3y=6
- Responder
-
no perpendicular
5x+2y=6;2x+5y=8
2x+4y=3;6x+3y=2
- Responder
-
no perpendicular
4x−2y=5;3x+6y=8
2x−6y=4;12x+4y=9
- Responder
-
perpendicular
6x−4y=5;8x+12y=3
8x−2y=7;3x+12y=9
- Responder
-
perpendicular
Matemáticas cotidianas
La ecuaciónC=59F−17.8 puede ser utilizada para convertir temperaturasF, en la escala Fahrenheit a temperaturas,C, en la escala Celsius.
- Explique qué significa la pendiente de la ecuación.
- Explique qué significa laC -intercepción de la ecuación.
La ecuaciónn=4T−160 se utiliza para estimar el número de chirps de grillo,n, en un minuto con base en la temperatura en grados Fahrenheit,T.
- Explique qué significa la pendiente de la ecuación.
- Explique qué significa lan -intercepción de la ecuación. ¿Es esta una situación realista?
- Responder
-
- Por cada incremento de un grado Fahrenheit, el número de chirps aumenta en cuatro.
- Habría−160 chícharos cuando la temperatura de Fahrenheit es0°. (Observe que esto no tiene sentido; este modelo no se puede utilizar para todas las temperaturas posibles).
Ejercicios de escritura
Explica con tus propias palabras cómo decidir qué método usar para graficar una línea.
¿Por qué todas las líneas horizontales son paralelas?
- Responder
-
Las respuestas variarán.
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
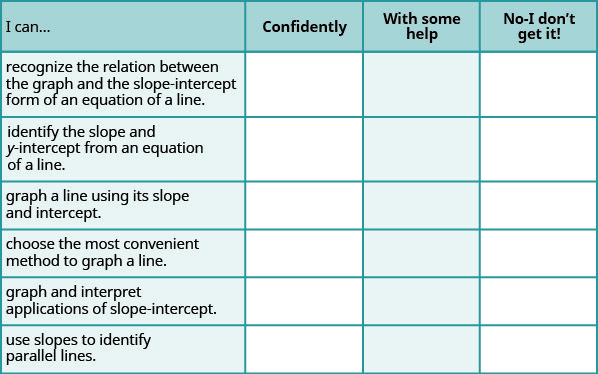
b. después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?


