4.6E: Ejercicios
- Page ID
- 110241
La práctica hace la perfección
Encontrar una ecuación de la línea dada la pendiente y\(y\) - Interceptar
En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente e\(y\) intercepción dadas. Escribe la ecuación en forma de pendiente-intercepción.
pendiente\(3\) e\(y\) intercepción\((0,5)\)
pendiente\(4\) e\(y\) intercepción\((0,1)\)
- Contestar
-
\(y=4x+1\)
pendiente\(6\) e\(y\) intercepción\((0,−4)\)
pendiente\(8\) e\(y\) intercepción\((0,−6)\)
- Contestar
-
\(y=8x−6\)
pendiente\(−1\) e\(y\) intercepción\((0,3)\)
pendiente\(−1\) e\(y\) intercepción\((0,7)\)
- Contestar
-
\(y=−x+7\)
pendiente\(−2\) e\(y\) intercepción\((0,−3)\)
pendiente\(−3\) e\(y\) intercepción\((0,−1)\)
- Contestar
-
\(y=−3x−1\)
pendiente\(\frac{3}{5}\) e\(y\) intercepción\((0,-1)\)
pendiente\(\frac{1}{5}\) e\(y\) intercepción\((0,-5)\)
- Contestar
-
\(y=\frac{1}{5} x-5\)
pendiente\(-\frac{3}{4}\) e\(y\) intercepción\((0,-2)\)
pendiente\(-\frac{2}{3}\) e\(y\) intercepción\((0,-3)\)
- Contestar
-
\(y=-\frac{2}{3} x-3\)
pendiente\(0\) e\(y\) intercepción\((0,-1)\)
pendiente\(0\) e\(y\) intercepción\((0,2)\)
- Contestar
-
\(y=2\)
pendiente\(-3\) e\(y\) intercepción\((0,0)\)
pendiente\(-4\) e\(y\) intercepción\((0,0)\)
- Contestar
-
\(y=−4x\)
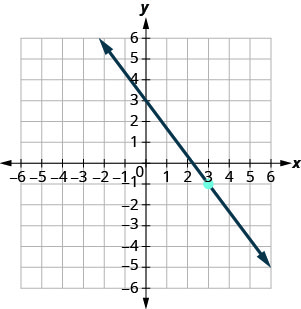
En los siguientes ejercicios, encuentra la ecuación de la línea que se muestra en cada gráfica. Escribe la ecuación en forma de pendiente-intercepción.
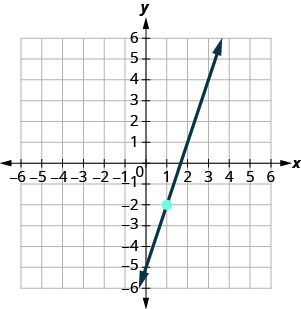
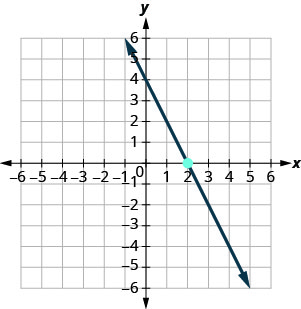
- Contestar
-
\(y=−2x+4\)
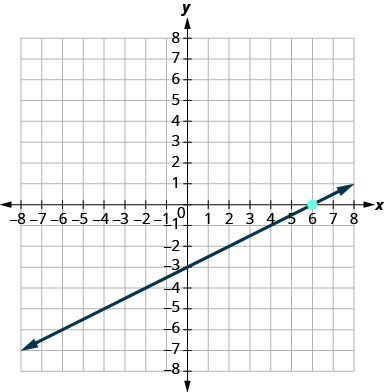
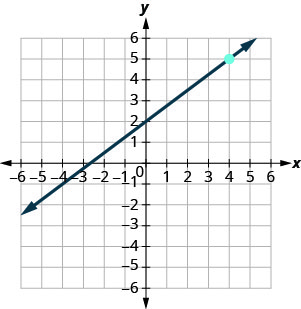
- Contestar
-
\(y=\frac{3}{4} x+2\)
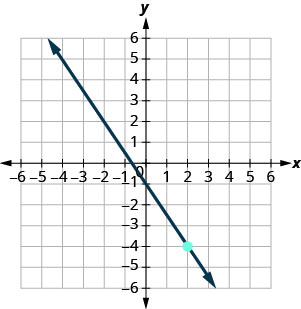
- Contestar
-
\(y=-\frac{3}{2} x-1\)
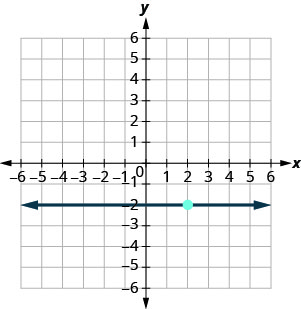
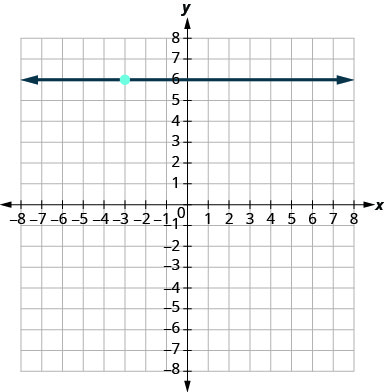
- Contestar
-
\(y=6\)
Encontrar una ecuación de la línea dada la pendiente y un punto
En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente dada y que contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.
\(m=\frac{5}{8},\)punto\((8,3)\)
\(m=\frac{3}{8},\)punto\((8,2)\)
- Contestar
-
\(y=\frac{3}{8} x-1\)
\(m=\frac{1}{6},\)punto\((6,1)\)
\(m=\frac{5}{6},\)punto\((6,7)\)
- Contestar
-
\(y=\frac{5}{6} x+2\)
\(m=-\frac{3}{4},\)punto\((8,-5)\)
\(m=-\frac{3}{5},\)punto\((10,-5)\)
- Contestar
-
\(y=-\frac{3}{5} x+1\)
\(m=-\frac{1}{4},\)punto\((-12,-6)\)
\(m=-\frac{1}{3},\)punto\((-9,-8)\)
- Contestar
-
\(y=-\frac{1}{3} x-11\)
Línea horizontal que contiene\((−2,5)\)
Línea horizontal que contiene\((−1,4)\)
- Contestar
-
\(y=4\)
Línea horizontal que contiene\((−2,−3)\)
Línea horizontal que contiene\((−1,−7)\)
- Contestar
-
\(y=−7\)
\(m=-\frac{3}{2},\)punto\((-4,-3)\)
\(m=-\frac{5}{2},\)punto\((-8,-2)\)
- Contestar
-
\(y=-\frac{5}{2} x-22\)
\(m=-7,\)punto\((-1,-3)\)
\(m=-4,\)punto\((-2,-3)\)
- Contestar
-
\(y=-4 x-11\)
Línea horizontal que contiene\((2,-3)\)
Línea horizontal que contiene\((4,-8)\)
- Contestar
-
\(y=−8\)
Encontrar una ecuación de la línea dada dos puntos
En los siguientes ejercicios, encuentra la ecuación de una línea que contiene los puntos dados. Escribe la ecuación en forma de pendiente-intercepción.
\((2,6)\)y\((5,3)\)
\((3,1)\)y\((2,5)\)
- Contestar
-
\(y=−4x+13\)
\((4,3)\)y\((8,1)\)
\((2,7)\)y\((3,8)\)
- Contestar
-
\(y=x+5\)
\((−3,−4)\)y\((5−2)\)
\((−5,−3)\)y\((4,−6)\)
- Contestar
-
\(y=-\frac{1}{3} x-\frac{14}{3}\)
\((−1,3)\)y\((−6,−7)\)
\((−2,8)\)y\((−4,−6)\)
- Contestar
-
\(y=7x+22\)
\((6,−4)\)y\((−2,5)\)
\((3,−2)\)y\((−4,4)\)
- Contestar
-
\(y=-\frac{6}{7} x+\frac{4}{7}\)
\((0,4)\)y\((2,−3)\)
\((0,−2)\)y\((−5,−3)\)
- Contestar
-
\(y=\frac{1}{5} x-2\)
\((7,2)\)y\((7,−2)\)
\((4,2)\)y\((4,−3)\)
- Contestar
-
\(x=4\)
\((−7,−1)\)y\((−7,−4)\)
\((−2,1)\)y\((−2,−4)\)
- Contestar
-
\(x=−2\)
\((6,1)\)y\((0,1)\)
\((6,2)\)y\((−3,2)\)
- Contestar
-
\(y=2\)
\((3,−4)\)y\((5,−4)\)
\((−6,−3)\)y\((−1,−3)\)
- Contestar
-
\(y=−3\)
\((4,3)\)y\((8,0)\)
\((0,0)\)y\((1,4)\)
- Contestar
-
\(y=4x\)
\((−2,−3)\)y\((−5,−6)\)
\((−3,0)\)y\((−7,−2)\)
- Contestar
-
\(y=\frac{1}{2} x+\frac{3}{2}\)
\((8,−1)\)y\((8,−5)\)
\((3,5)\)y\((−7,5)\)
- Contestar
-
\(y=5\)
Encontrar una ecuación de una línea paralela a una línea dada
En los siguientes ejercicios, encuentra una ecuación de una línea paralela a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.
\(y=4 x+2,\)punto de línea\((1,2)\)
\(y=3 x+4,\)punto de línea\((2,5)\)
- Contestar
-
\(y=3 x-1\)
\(y=-2 x-3,\)punto de línea\((-1,3)\)
\(y=-3x-1,\)punto de línea\((2,-3)\)
- Contestar
-
\(y=−3x+3\)
\(3 x-y=4,\)punto de línea\((3,1)\)
\(2 x-y=6,\)punto de línea\((3,0)\)
- Contestar
-
\(y=2x−6\)
\(4 x+3 y=6,\)punto de línea\((0,-3)\)
\(2x+3y=6,\)punto de línea\((0,5)\)
- Contestar
-
\(y=-\frac{2}{3} x+5\)
\(x=-3,\)punto de línea\((-2,-1)\)
\(x=-4,\)punto de línea\((-3,-5)\)
- Contestar
-
\(x=−3\)
\(x-2=0,\)punto de línea\((1,-2)\)
\(x-6=0,\)punto de línea\((4,-3)\)
- Contestar
-
\(x=4\)
\(y=5,\)punto de línea\((2,-2)\)
\(y=1,\)punto de línea\((3,-4)\)
- Contestar
-
\(y=−4\)
\(y+2=0,\)punto de línea\((3,-3)\)
\(y+7=0,\)punto de línea\((1,-1)\)
- Contestar
-
\(y=−1\)
Encontrar una ecuación de una línea perpendicular a una línea dada
En los siguientes ejercicios, encuentra una ecuación de una línea perpendicular a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.
\(y=-2 x+3,\)punto de línea\((2,2)\)
\(y=-x+5,\)punto de línea\((3,3)\)
- Contestar
-
\(y=x\)
\(y=\frac{3}{4} x-2,\)punto de línea\((-3,4)\)
\(y=\frac{2}{3} x-4,\)punto de línea\((2,-4)\)
- Contestar
-
\(y=-\frac{3}{2} x-1\)
\(2 x-3 y=8,\)punto de línea\((4,-1)\)
\(4 x-3 y=5,\)punto de línea\((-3,2)\)
- Contestar
-
\(y=-\frac{3}{4} x-\frac{1}{4}\)
\(2 x+5 y=6,\)punto de línea\((0,0)\)
\(4 x+5 y=-3,\)punto de línea\((0,0)\)
- Contestar
-
\(y=\frac{5}{4} x\)
\(y-3=0,\)punto de línea\((-2,-4)\)
\(y-6=0,\)punto de línea\((-5,-3)\)
- Contestar
-
\(x=-5\)
\(y\)eje de línea, punto\((3,4)\)
\(y\)eje de línea, punto\((2,1)\)
- Contestar
-
\(y=1\)
Práctica Mixta
En los siguientes ejercicios, encuentra la ecuación de cada línea. Escribe la ecuación en forma de pendiente-intercepción.
Conteniendo los puntos\((4,3)\) y\((8,1)\)
Conteniendo los puntos\((2,7)\) y\((3,8)\)
- Contestar
-
\(y=x+5\)
\(m=\frac{1}{6},\)que contiene punto\((6,1)\)
\(m=\frac{5}{6},\)que contiene punto\((6,7)\)
- Contestar
-
\(y=\frac{5}{6} x+2\)
Paralelo a la línea\(4 x+3 y=6,\) que contiene el punto\((0,-3)\)
Paralelo a la línea\(2 x+3 y=6,\) que contiene el punto\((0,5)\)
- Contestar
-
\(y=-\frac{2}{3} x+5\)
\(m=-\frac{3}{4},\)que contiene punto\((8,-5)\)
\(m=-\frac{3}{5},\)que contiene punto\((10,-5)\)
- Contestar
-
\(y=-\frac{3}{5} x+1\)
Ppendicularmente al\(y-1=0,\) punto de línea\((-2,6)\)
Perpendiculares a la línea eje y, punto\((-6,2)\)
- Contestar
-
\(y=2\)
Conteniendo los puntos\((4,3)\) y\((8,1)\)
Conteniendo los puntos\((-2,0)\) y\((-3,-2)\)
- Contestar
-
\(y=x+2\)
Paralelo a la línea\(x=-3,\) que contiene el punto\((-2,-1)\)
Paralelo a la línea\(x=-4,\) que contiene el punto\((-3,-5)\)
- Contestar
-
\(x=-3\)
Conteniendo los puntos\((-3,-4)\) y\((2,-5)\)
Conteniendo los puntos\((-5,-3)\) y\((4,-6)\)
- Contestar
-
\(y=-\frac{1}{3} x-\frac{14}{3}\)
perpendicular a la línea\(x-2 y=5,\) que contiene el punto\((-2,2)\)
perpendicular a la línea\(4 x+3 y=1,\) que contiene el punto\((0,0)\)
- Contestar
-
\(y=\frac{3}{4} x\)
Matemáticas cotidianas
Colesterol. La edad,\(x,\) y nivel de colesterol LDL,\(y,\) de dos hombres están dadas por los puntos\((18,68)\) y\((27,122) .\) Encuentra una ecuación lineal que modele la relación entre la edad y el nivel de colesterol LDL.
Consumo de combustible. La ciudad mpg,\(x\), y autopista mpg,\(y,\) de dos autos están dadas por los puntos\((29,40)\) y\((19,28) .\) Encuentra una ecuación
lineal que modela la relación entre ciudad mpg y autopista mp.
- Contestar
-
\(y=1.2 x+5.2\)
Ejercicios de escritura
¿Por qué todas las líneas horizontales son paralelas?
Explica con tus propias palabras por qué las pendientes de dos líneas perpendiculares deben tener signos opuestos.
- Contestar
-
Las respuestas variarán.
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
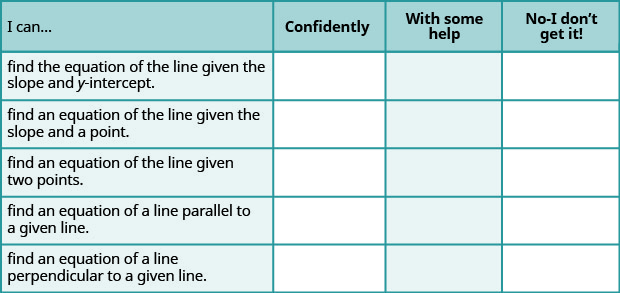
b. En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?


