4.7: Gráficas de Desigualdades Lineales
- Page ID
- 110252
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Verificar soluciones a una desigualdad en dos variables
- Reconocer la relación entre las soluciones de una desigualdad y su gráfica
- Graficar desigualdades lineales
Antes de comenzar, toma este cuestionario de preparación.
- Resolver:\(4x+3>23.\)
Si te perdiste este problema, revisa Ejercicio 2.7.22. - Traducir del álgebra al inglés:\(x<5.\)
Si te perdiste este problema, revisa el Ejercicio 1.3.1. - Evalúa\(3x−2y\) cuándo\(x=1, \, y=−2.\)
Si te perdiste este problema, revisa Ejercicio 1.5.28.
Verificar soluciones a una desigualdad en dos variables
Hemos aprendido a resolver las desigualdades en una variable. Ahora, veremos las desigualdades en dos variables. Las desigualdades en dos variables tienen muchas aplicaciones. Si diriges un negocio, por ejemplo, querrías que tus ingresos fueran mayores que tus costos, para que tu negocio obtuviera ganancias.
Una desigualdad lineal es una desigualdad que se puede escribir en una de las siguientes formas:
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]
donde\(A\) y no\(B\) son ambos cero.
¿Recuerdas que una desigualdad con una variable tenía muchas soluciones? La solución a la desigualdad\(x>3\) es cualquier número mayor que\(3\). Mostramos esto en la recta numérica sombreando en la recta numérica a la derecha de\(3\), y poniendo un paréntesis abierto en\(3\). Ver Figura\(\PageIndex{1}\).

De igual manera, las desigualdades en dos variables tienen muchas soluciones. Cualquier par ordenado\( (x, y)\) que haga verdadera la desigualdad cuando sustituimos en los valores es una solución de la desigualdad.
Un par ordenado\( (x, y)\) es una solución de una desigualdad lineal si la desigualdad es cierta cuando sustituimos los valores de\(x\) y\(y\).
Determine si cada par ordenado es una solución a la desigualdad\(y>x+4\):
- \((0,0)\)
- \((1,6)\)
- \((2,6)\)
- \((−5,−15)\)
- \((−8,12)\)
- Contestar
- 1.
2.\((0,0)\) 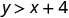

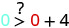
Simplificar. 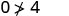
Entonces, no\((0,0)\) es una solución para\(y>x+4\).\((1,6)\) 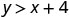

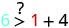
Simplificar. 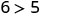
Entonces,\((1,6)\) es una solución para\(y>x+4\). - 3.
\((2,6)\) 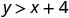


Simplificar. 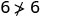
Entonces, no\((2,6)\) es una solución para\(y>x+4\). - 4.
\((−5,−15)\) 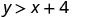
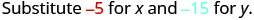
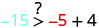
Simplificar. 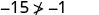
Entonces, no\((−5,−15)\) es una solución para\(y>x+4\). - 5.
(−8,12) 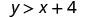

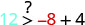
Simplificar. 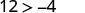
Entonces,\((−8,12)\) es una solución para\(y>x+4\).
Determine si cada par ordenado es una solución a la desigualdad\(y>x−3\):
- \((0,0)\)
- \((4,9)\)
- \((−2,1)\)
- \((−5,−3)\)
- \((5,1)\)
- Contestar
-
- si
- si
- si
- si
- no
Determine si cada par ordenado es una solución a la desigualdad\(y<x+1\):
- \((0,0)\)
- \((8,6)\)
- \((−2,−1)\)
- \((3,4)\)
- \((−1,−4)\)
- Contestar
-
- si
- si
- no
- no
- si
Reconocer la relación entre las soluciones de una desigualdad y su gráfica
Ahora, veremos cómo las soluciones de una desigualdad se relacionan con su gráfica.
Volvamos a pensar en la recta numérica de la Figura\(\PageIndex{1}\). El punto\(x=3\) separó esa recta numérica en dos partes. En un lado de\(3\) están todos los números menores que\(3\). En el otro lado de\(3\) todos los números son mayores que\(3\). Ver Figura\(\PageIndex{2}\).
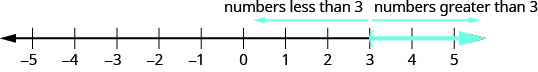
La solución a\(x>3\) es la parte sombreada de la recta numérica a la derecha de\(x=3\).
Del mismo modo, la línea\(y=x+4\) separa el plano en dos regiones. En un lado de la línea hay puntos con\(y<x+4\). Al otro lado de la línea están los puntos con\(y>x+4\). Llamamos a la línea\(y=x+4\) línea límite.
La línea con ecuación\(Ax+By=C\) es la línea límite que separa la región donde\(Ax+By>C\) de la región donde\(Ax+By<C\).
Para una desigualdad en una variable, el punto final se muestra con un paréntesis o un paréntesis dependiendo de si aa está incluido o no en la solución:

De igual manera, para una desigualdad en dos variables, la línea límite se muestra con una línea continua o discontinua para indicar si la línea está incluida o no en la solución. Esto se resume en la Tabla\(\PageIndex{1}\).
| \(Ax+By<C\) | \(Ax+By\leq C\) |
| \(Ax+By>C\) | \(Ax+By\geq C\) |
| La línea límite no está incluida en la solución. | La línea límite está incluida en la solución. |
| La línea límite está discontinua. | La línea límite es sólida. |
Ahora, echemos un vistazo a lo que encontramos en Ejercicio\(\PageIndex{1}\). Empezaremos graficando la línea\(y=x+4\), y luego trazaremos los cinco puntos que probamos. Ver Figura\(\PageIndex{3}\).
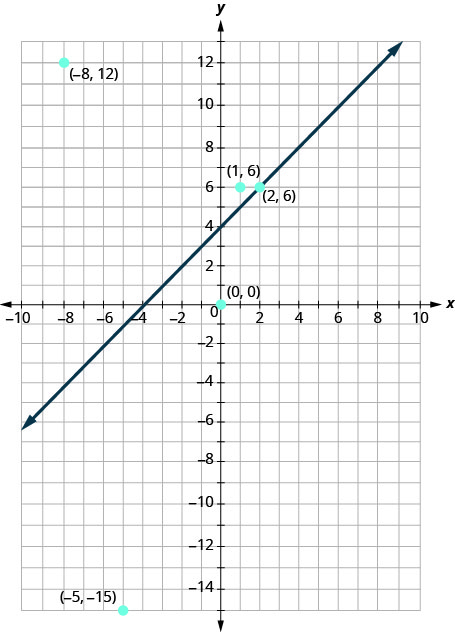
En Ejercicio\(\PageIndex{1}\) encontramos que algunos de los puntos eran soluciones a la desigualdad\(y>x+4\) y otros no.
¿Cuáles de los puntos que trazamos son soluciones a la desigualdad\(y>x+4\)? Los puntos\((1,6)\) y\((−8,12)\) son soluciones a la desigualdad\(y>x+4\). Observe que ambos están en el mismo lado de la línea de límite\(y=x+4\).
Los dos puntos\((0,0)\) y\((−5,−15)\) están al otro lado de la línea limítrofe\(y=x+4\), y no son soluciones a la desigualdad\(y>x+4\). Para esos dos puntos,\(y<x+4\).
¿Qué pasa con el punto\((2,6)\)? Porque\(6=2+4\), el punto es una solución a la ecuación\(y=x+4\). Entonces el punto\((2,6)\) está en la línea límite.
Tomemos otro punto del lado izquierdo de la línea límite y probemos si es o no una solución a la desigualdad\(y>x+4\). El punto\((0,10)\) claramente parece estar a la izquierda de la línea fronteriza, ¿no? ¿Es una solución a la desigualdad?
\[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]
Cualquier punto que elija en el lado izquierdo de la línea de límite es una solución a la desigualdad\(y>x+4\). Todos los puntos de la izquierda son soluciones.
De igual manera, todos los puntos del lado derecho de la línea límite, el lado con\((0,0)\) y\((−5,−15)\), no son soluciones a\(y>x+4\). Ver Figura\(\PageIndex{4}\).
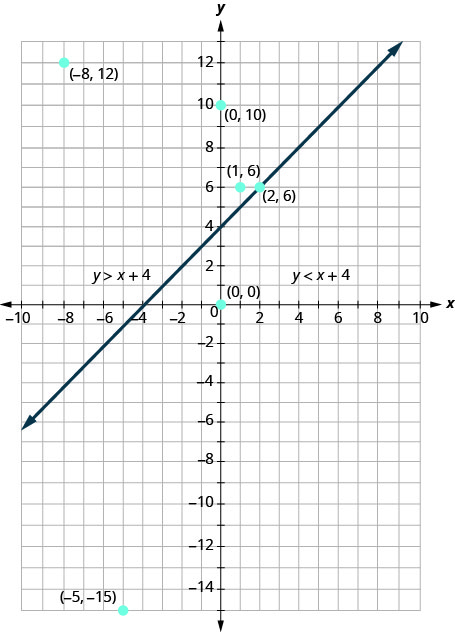
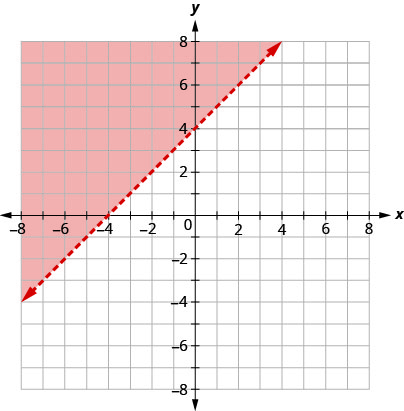
La gráfica de la desigualdad\(y>x+4\) se muestra en la Figura\(\PageIndex{5}\) siguiente. La línea\(y=x+4\) divide el plano en dos regiones. El lado sombreado muestra las soluciones a la desigualdad\(y>x+4\).
Los puntos en la línea límite, aquellos donde\(y=x+4\), no son soluciones a la desigualdad\(y>x+4\), por lo que la línea en sí no es parte de la solución. Lo demostramos haciendo la línea discontinua, no sólida.
La línea límite que se muestra es\(y=2x−1\). Escribe la desigualdad que muestra la gráfica.
- Contestar
-
La línea\(y=2x−1\) es la línea límite. En un lado de la línea están los puntos con\(y>2x−1\) y en el otro lado de la línea están los puntos con\(y<2x−1\).
Probemos el punto\((0,0)\) y veamos qué desigualdad describe su lado de la línea límite.
At\((0,0)\), que la desigualdad es verdadera:
\[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]
Ya que\(y>2x−1\) es cierto, el lado de la línea con\((0,0)\), es la solución. La región sombreada muestra la solución de la desigualdad\(y>2x−1\).
Dado que la línea límite se grafica con una línea continua, la desigualdad incluye el signo igual.
La gráfica muestra la desigualdad\(y\geq 2x−1\).
Podríamos usar cualquier punto como punto de prueba, siempre que no esté en la línea. ¿Por qué elegimos\((0,0)\)? Porque es lo más fácil de evaluar. Es posible que desee elegir un punto en el otro lado de la línea de límite y verificarlo\(y<2x−1\).
Escribe la desigualdad que muestra la gráfica con la línea límite\(y=−2x+3\).
- Contestar
-
\(y\geq −2x+3\)
Escribe la desigualdad que muestra la gráfica con la línea límite\(y=\frac{1}{2}x−4\).
- Contestar
-
\(y \leq \frac{1}{2}x - 4\)
La línea límite que se muestra es\(2x+3y=6\). Escribe la desigualdad que muestra la gráfica.
- Contestar
-
La línea\(2x+3y=6\) es la línea límite. En un lado de la línea están los puntos con\(2x+3y>6\) y en el otro lado de la línea están los puntos con\(2x+3y<6\).
Probemos el punto\((0,0)\) y veamos qué desigualdad describe su lado de la línea límite.
At\((0,0)\), que la desigualdad es verdadera:
\[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]
Entonces el lado con\((0,0)\) es el lado donde\(2x+3y<6\).
(Es posible que desee elegir un punto en el otro lado de la línea de límite y verificarlo)\(2x+3y>6\).
Dado que la línea límite se grafica como una línea discontinua, la desigualdad no incluye un signo igual.
La gráfica muestra la solución a la desigualdad\(2x+3y<6\).
Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite\(x−4y=8\).
- Contestar
-
\(x-4 y \leq 8\)
Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite\(3x−y=6\).
- Contestar
-
\(3 x-y \leq 6\)
Graficar desigualdades lineales
Ahora, estamos listos para juntar todo esto para graficar las desigualdades lineales.
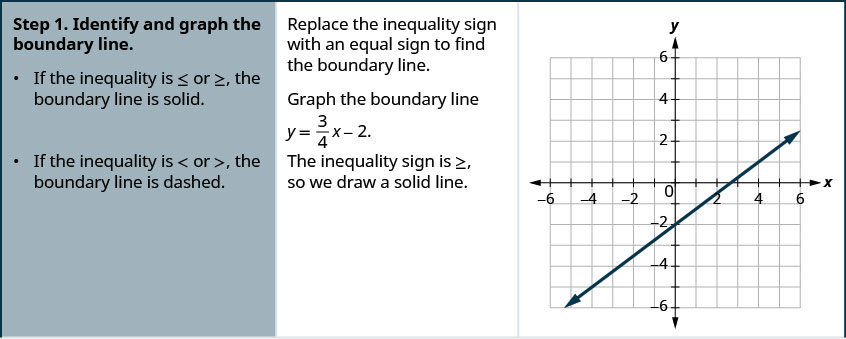
Grafica la desigualdad lineal\(y \geq \frac{3}{4} x-2\).
- Contestar
-

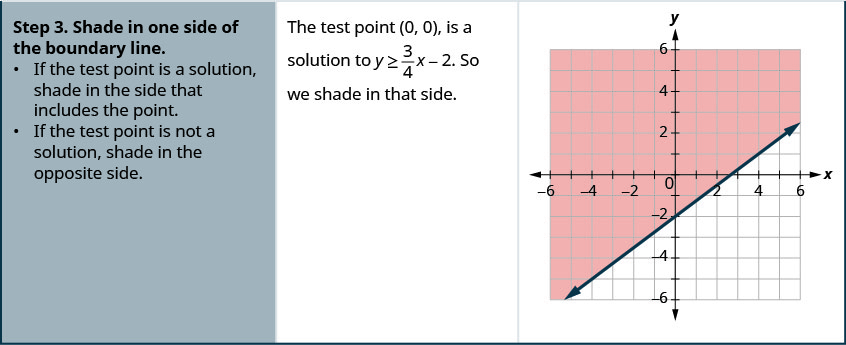
Grafica la desigualdad lineal\(y \geq \frac{5}{2} x-4\).
- Contestar
-
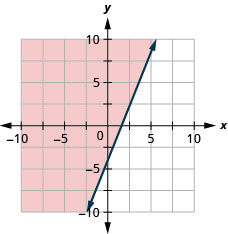
Grafica la desigualdad lineal\(y<\frac{2}{3} x-5\).
- Contestar
-
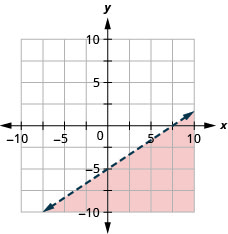
Aquí se resumen los pasos que damos para graficar una desigualdad lineal.
- Identificar y graficar la línea límite.
- Si la desigualdad es\(≤\) o\(≥\), la línea límite es sólida.
- Si la desigualdad es\(<\) o\(>\), la línea límite es discontinua.
- Pruebe un punto que no esté en la línea límite. ¿Es una solución de la desigualdad?
- Sombra en un lado de la línea límite.
- Si el punto de prueba es una solución, sombra en el lado que incluye el punto.
- Si el punto de prueba no es una solución, sombree en el lado opuesto.
Grafica la desigualdad lineal\(x−2y<5\).
- Contestar
-
Primero graficamos la línea límite\(x−2y=5\). La desigualdad es\(<\) así que trazamos una línea discontinua.
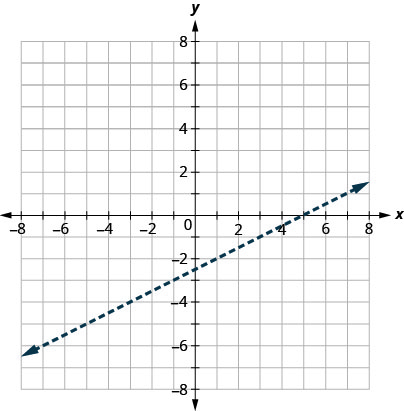
-
Entonces probamos un punto. Volveremos a usar\((0,0)\) porque es fácil de evaluar y no está en la línea límite.
Es\((0,0)\) una solución de\(x−2y<5\)?
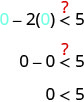
El punto\((0,0)\) es una solución de\(x−2y<5\), así que sombreamos en ese lado de la línea limítrofe.
Grafica la desigualdad lineal\(2x−3y\leq 6\).
- Contestar
-
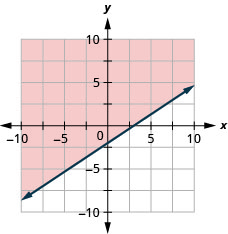
Grafica la desigualdad lineal\(2x−y>3\).
- Contestar
-
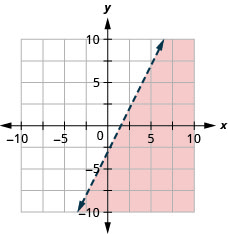
¿Y si la línea límite pasa por el origen? Entonces no podremos usar\((0,0)\) como punto de prueba. No hay problema, solo elegiremos algún otro punto que no esté en la línea límite.
Grafica la desigualdad lineal\(y\leq −4x\).
- Contestar
-
Primero graficamos la línea límite\(y=−4x\). Está en forma de pendiente—intercepción, con\(m=−4\) y\(b=0\). La desigualdad es\(≤\) así que trazamos una línea sólida.
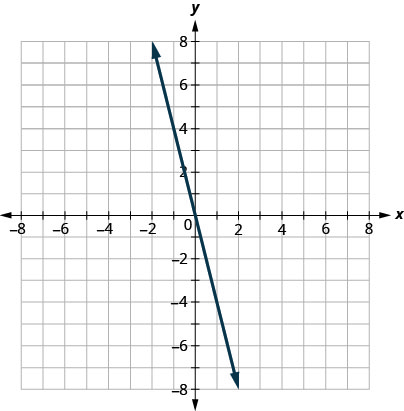
Ahora, necesitamos un punto de prueba. Podemos ver que el punto no\((1,0)\) está en la línea limítrofe.
Es\((1,0)\) una solución de\(y≤−4x\)?
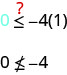
El punto no\((1,0)\) es una solución para\(y≤−4x\), así que sombreamos en el lado opuesto de la línea limítrofe. Ver Figura\(\PageIndex{6}\).
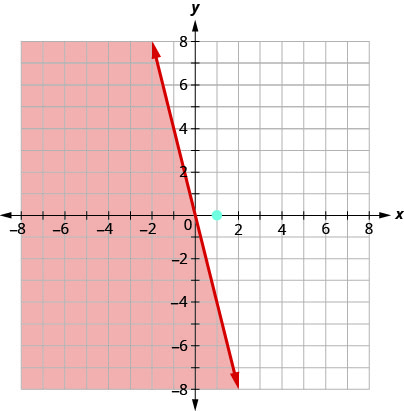
Figura\(\PageIndex{6}\)
Grafica la desigualdad lineal\(y>−3x\).
- Contestar
-
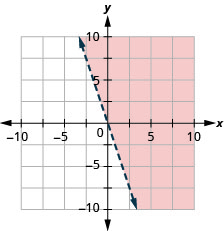
Grafica la desigualdad lineal\(y\geq −2x\).
- Contestar
-
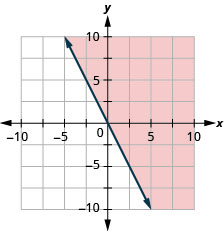
Algunas desigualdades lineales tienen sólo una variable. Pueden tener un\(x\) pero no\(y\), o un\(y\) pero no\(x\). En estos casos, la línea límite será una línea vertical u horizontal. ¿Te acuerdas?
\(\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}\)
Grafica la desigualdad lineal\(y>3\).
- Contestar
-
Primero graficamos la línea límite\(y=3\). Se trata de una línea horizontal. La desigualdad es\(>\) así que trazamos una línea discontinua.
Probamos el punto\((0,0)\).
\[y>3 \\ 0\not>3\]
\((0,0)\)no es una solución para\(y>3\).
Entonces sombreamos el lado que no incluye\((0,0)\).
Grafica la desigualdad lineal\(y<5\).
- Contestar
-
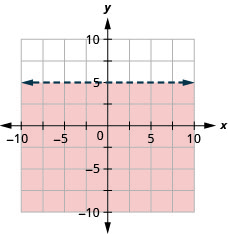
Grafica la desigualdad lineal\(y \leq-1\).
- Contestar
-
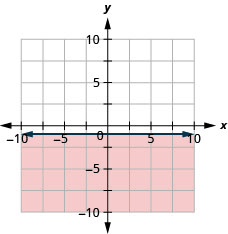
Conceptos clave
- Para graficar una desigualdad lineal
- Identificar y graficar la línea límite.
Si la desigualdad es\(≤\) o\(≥\), la línea límite es sólida.
Si la desigualdad es\(<\) o\(>\), la línea límite es discontinua. - Pruebe un punto que no esté en la línea límite. ¿Es una solución de la desigualdad?
- Sombra en un lado de la línea límite.
Si el punto de prueba es una solución, sombra en el lado que incluye el punto.
Si el punto de prueba no es una solución, sombree en el lado opuesto.
- Identificar y graficar la línea límite.
Glosario
- línea límite
- La línea con ecuación\(A x+B y=C\) que separa la región donde\(A x+B y>C\) de la región donde\(A x+B y<C\).
- desigualdad lineal
- Una desigualdad que se puede escribir en una de las siguientes formas:
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]
donde\(A\) y no\(B\) son ambos cero.
- solución de una desigualdad lineal
- Un par ordenado\((x,\,y)\) es una solución a una desigualdad lineal la desigualdad es cierta cuando sustituimos los valores de\(x\) y\(y\).


