4.7E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 110260

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Verificar soluciones a una desigualdad en dos variables

En los siguientes ejercicios, determinar si cada par ordenado es una solución a la desigualdad dada.

Ejercicio$\PageIndex{1}$

Determine si cada par ordenado es una solución a la desigualdad$y>x−1$:

$(0,1)$
$(−4,−1)$
$(4,2)$
$(3,0)$
$(−2,−3)$

Ejercicio$\PageIndex{2}$

Determine si cada par ordenado es una solución a la desigualdad$y>x−3$:

$(0,0)$
$(2,1)$
$(−1,−5)$
$(−6,−3)$
$(1,0)$

Contestar

Ejercicio$\PageIndex{3}$

Determine si cada par ordenado es una solución a la desigualdad$y<x+2$:

$(0,3)$
$(−3,−2)$
$(−2,0)$
$(0,0)$
$(−1,4)$

Ejercicio$\PageIndex{4}$

Determine si cada par ordenado es una solución a la desigualdad$y<x+5$:

$(−3,0)$
$(1,6)$
$(−6,−2)$
$(0,1)$
$(5,−4)$

Contestar

Ejercicio$\PageIndex{5}$

Determine si cada par ordenado es una solución a la desigualdad$x+y>4$:

$(5,1)$
$(−2,6)$
$(3,2)$
$(10,−5)$
$(0,0)$

Ejercicio$\PageIndex{6}$

Determine si cada par ordenado es una solución a la desigualdad$x+y>2$:

$(1,1)$
$(4,−3)$
$(0,0)$
$(−8,12)$
$(3,0)$

Contestar

Reconocer la relación entre las soluciones de una desigualdad y su gráfica

En los siguientes ejercicios, escriba la desigualdad mostrada por la región sombreada.

Ejercicio$\PageIndex{7}$

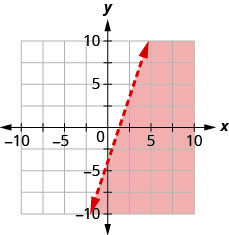
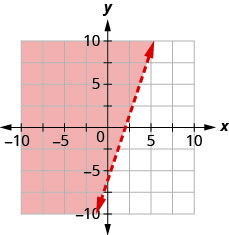
Escribe la desigualdad que muestra la gráfica con la línea límite$y=3x−4$.

$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a 3x menos 4 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región a la derecha de la línea está sombreada.$

Ejercicio$\PageIndex{8}$

Escribe la desigualdad que muestra la gráfica con la línea límite$y=2x−4$.

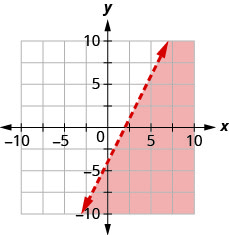
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a 2x menos 4 se traza como una línea continua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Contestar: $y<2 x-4$

Ejercicio$\PageIndex{9}$

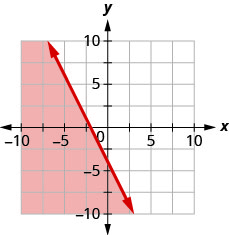
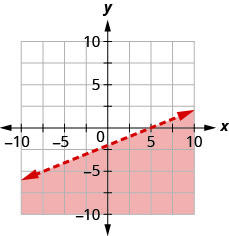
Escribe la desigualdad que muestra la gráfica con la línea de límite$y=\frac{1}{2} x+1$

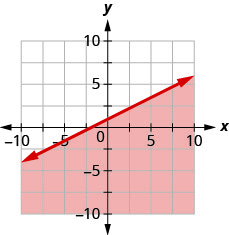
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a la mitad negativa x más 1 se traza como una línea continua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{10}$

Escribe la desigualdad que muestra la gráfica con la línea de límite$y=-\frac{1}{3} x-2$

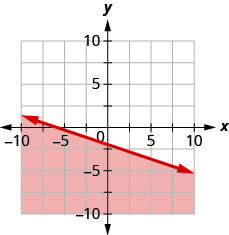
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a un tercio negativo x menos 2 se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región debajo de la línea está sombreada.$

Contestar: $y \leq-\frac{1}{3} x-2$

Ejercicio$\PageIndex{11}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x+y=5$.

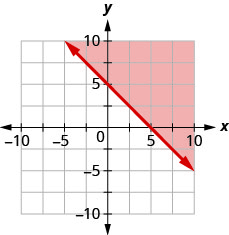
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x más y es igual a 5 se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región por encima de la línea está sombreada.$

Ejercicio$\PageIndex{12}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x+y=3$.

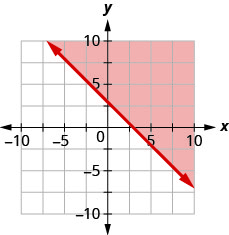
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x más y es igual a 3 se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región por encima de la línea está sombreada.$

Contestar: $x+y \geq 3$

Ejercicio$\PageIndex{13}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$2x+y=−4$.

$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea 2 x más y es igual a 4 negativo se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{14}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x+2y=−2$.

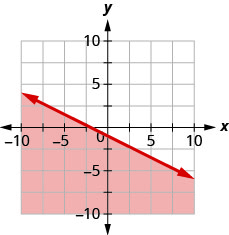
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x más 2 y es igual a negativo 2 se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región debajo de la línea está sombreada.$

Contestar: $x+2 y \geq-2$

Ejercicio$\PageIndex{15}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$3x−y=6$.

$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea 3 x menos y es igual a 6 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región a la izquierda de la línea está sombreada.$

Ejercicio$\PageIndex{16}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$2x−y=4$.

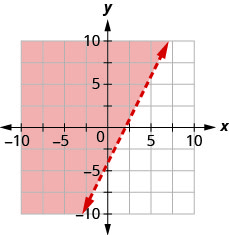
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea 2 x menos y es igual a 4 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región a la izquierda de la línea está sombreada.$

Contestar: $2 x-y<4$

Ejercicio$\PageIndex{17}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$2x−5y=10$.

$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea 2 x menos 5 y es igual a 10 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{18}$

Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$4x−3y=12$.

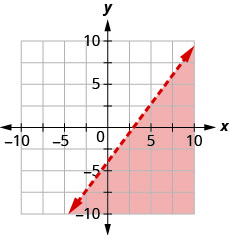
$La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea 4 x menos 3 y es igual a 12 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Contestar: $4 x-3 y>12$

Graficar desigualdades lineales

En los siguientes ejercicios, grafica cada desigualdad lineal.

Ejercicio$\PageIndex{19}$

Graficar la desigualdad lineal$y>\frac{2}{3} x-1$

Ejercicio$\PageIndex{20}$

Graficar la desigualdad lineal$y<\frac{3}{5} x+2$

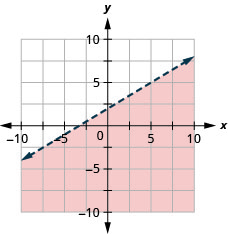
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a tres quintos x más 2 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{21}$

Graficar la desigualdad lineal$y \leq-\frac{1}{2} x+4$

Ejercicio$\PageIndex{22}$

Graficar la desigualdad lineal$y \geq-\frac{1}{3} x-2$

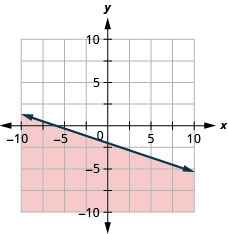
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a un tercio negativo x menos 2 se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{23}$

Graficar la desigualdad lineal$x-y \leq 3$

Ejercicio$\PageIndex{24}$

Graficar la desigualdad lineal$x-y \geq -2$

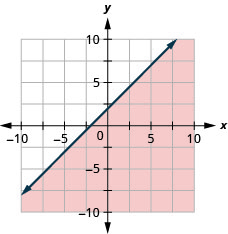
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x menos y es igual a negativo 2 se traza como una línea continua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{25}$

Graficar la desigualdad lineal$4x+y>-4$

Ejercicio$\PageIndex{26}$

Graficar la desigualdad lineal$x+5y<-5$

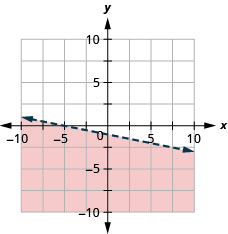
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x más 5 y es igual a 5 negativo se traza como una línea discontinua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{27}$

Graficar la desigualdad lineal$3 x+2 y \geq-6$

Ejercicio$\PageIndex{28}$

Graficar la desigualdad lineal$4 x+2 y \geq-8$

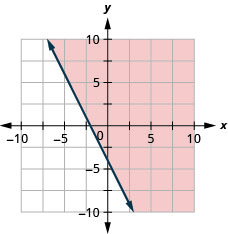
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea 4 x más 2 y es igual a 8 negativo se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región a la derecha de la línea está sombreada.$

Ejercicio$\PageIndex{29}$

Graficar la desigualdad lineal$y>4x$

Ejercicio$\PageIndex{30}$

Graficar la desigualdad lineal$y>x$

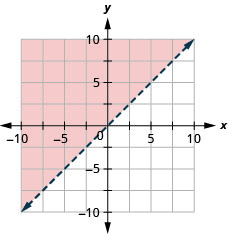
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a x se traza como una línea continua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región por encima de la línea está sombreada.$

Ejercicio$\PageIndex{31}$

Graficar la desigualdad lineal$y \leq-x$

Ejercicio$\PageIndex{32}$

Graficar la desigualdad lineal$y \leq-3 x$

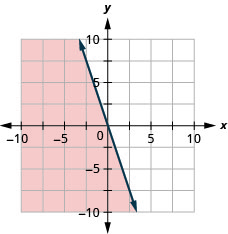
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a 3 x negativo se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región a la izquierda de la línea está sombreada.$

Ejercicio$\PageIndex{33}$

Graficar la desigualdad lineal$y \geq-2$

Ejercicio$\PageIndex{34}$

Graficar la desigualdad lineal$y<-1$

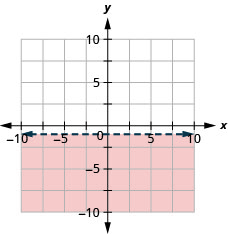
Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a 1 negativo se traza como una línea horizontal discontinua. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{35}$

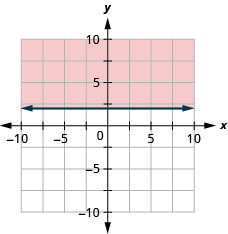
Graficar la desigualdad lineal$y<4$

Ejercicio$\PageIndex{36}$

Graficar la desigualdad lineal$y \geq 2$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a 2 se traza como una línea horizontal sólida. La región por encima de la línea está sombreada.$

Ejercicio$\PageIndex{37}$

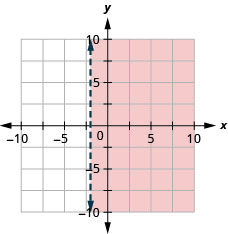
Graficar la desigualdad lineal$x \leq 5$

Ejercicio$\PageIndex{38}$

Graficar la desigualdad lineal$x>-2$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x es igual a negativo 2 se traza como una línea vertical discontinua. La región a la derecha de la línea está sombreada.$

Ejercicio$\PageIndex{39}$

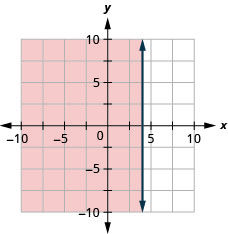
Graficar la desigualdad lineal$x>-3$

Ejercicio$\PageIndex{40}$

Graficar la desigualdad lineal$x \leq 4$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x es igual a 4 se traza como una línea vertical continua. La región a la izquierda de la línea está sombreada.$

Ejercicio$\PageIndex{41}$

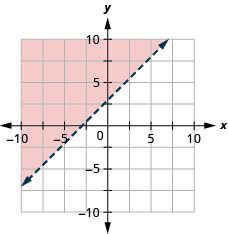
Graficar la desigualdad lineal$x-y<4$

Ejercicio$\PageIndex{42}$

Graficar la desigualdad lineal$x-y<-3$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x menos y es igual a negativo 3 se traza como una línea discontinua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región por encima de la línea está sombreada.$

Ejercicio$\PageIndex{43}$

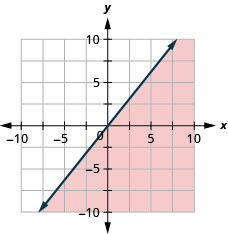
Graficar la desigualdad lineal$y \geq \frac{3}{2} x$

Ejercicio$\PageIndex{44}$

Graficar la desigualdad lineal$y \leq \frac{5}{4} x$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a cinco cuartos x se traza como una línea continua que se extiende desde la parte inferior izquierda hacia la parte superior derecha. La región debajo de la línea está sombreada.$

Ejercicio$\PageIndex{45}$

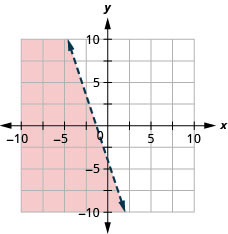
Graficar la desigualdad lineal$y>-2 x+1$

Ejercicio$\PageIndex{46}$

Graficar la desigualdad lineal$y<-3 x-4$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea y es igual a negativo 3 x menos 4 se traza como una línea discontinua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región a la izquierda de la línea está sombreada.$

Ejercicio$\PageIndex{47}$

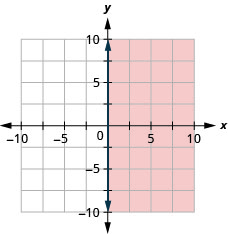
Graficar la desigualdad lineal$x \leq-1$

Ejercicio$\PageIndex{48}$

Graficar la desigualdad lineal$x \geq 0$

Contestar: $La gráfica muestra el plano de coordenadas x y. Los ejes x e y van cada uno de los negativos de 10 a 10. La línea x es igual a 0 negativo se traza como una línea vertical continua a lo largo del eje y. La región a la derecha de la línea está sombreada.$

Matemáticas cotidianas

Ejercicio$\PageIndex{49}$

Dinero. Gerry quiere tener un máximo de $100 en efectivo en la taquilla cuando abra el carnaval de su iglesia. Tendrá billetes de $1 y billetes de 5 dólares. Si$x$ es el número de billetes de $1 y$y$ es el número de billetes de 5 dólares, la desigualdad$x+5y \leq 100$ modela la situación.

Grafica la desigualdad.
Enumerar tres soluciones a la desigualdad$x+5y \leq 100$ donde ambos$x$ y$y$ son enteros.

Ejercicio$\PageIndex{50}$

Compras. Tula tiene $20 para gastar en la venta de libros usados. Los libros de tapa dura cuestan $2 cada uno y los libros de bolsillo cuestan $0.50 cada uno Si$x$ es el número de libros de tapa dura que Tula puede comprar y$y$ es el número de libros de bolsillo que puede comprar, la desigualdad$2x+\frac{1}{2} y \leq 20$ modela la situación.

Grafica la desigualdad.
Enumerar tres soluciones a la desigualdad$2x+\frac{1}{2} y \leq 20$ donde ambos$x$ y$y$ son números enteros.

Contestar

1.
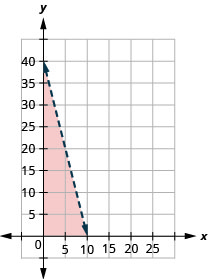
$La gráfica muestra el plano de coordenadas x y. El eje x va de 0 a 20 y el eje y va de 0 a 30. La línea 2 x más la mitad y es igual a 20 se traza como una línea continua que se extiende desde la parte superior izquierda hacia la parte inferior derecha. La región debajo de la línea está sombreada.$

2. Las respuestas variarán.

Ejercicios de escritura

Ejercicio$\PageIndex{51}$

Lester piensa que la solución de cualquier desigualdad con un$>$ signo es la región por encima de la línea y la solución de cualquier desigualdad con un$<$ signo es la región por debajo de la línea. ¿Lester está en lo correcto? Explique por qué o por qué no.

Ejercicio$\PageIndex{52}$

Explique por qué en algunas gráficas de desigualdades lineales la línea límite es sólida pero en otras gráficas es discontinua.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

$Esta es una tabla que tiene cuatro filas y cuatro columnas. En la primera fila, que es una fila de encabezado, las celdas leen de izquierda a derecha: “Puedo...”, “con confianza”, “con algo de ayuda” y “¡No-no lo consigo!” La primera columna debajo de “Puedo...” dice “verificar soluciones a una desigualdad en dos variables”, “reconocer la relación entre las soluciones de una desigualdad y su gráfica” y “graficar desigualdades lineales”. El resto de las celdas están en blanco.$

b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

La práctica hace la perfección

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Ejercicio\(\PageIndex{33}\)

Ejercicio\(\PageIndex{34}\)

Ejercicio\(\PageIndex{35}\)

Ejercicio\(\PageIndex{36}\)

Ejercicio\(\PageIndex{37}\)

Ejercicio\(\PageIndex{38}\)

Ejercicio\(\PageIndex{39}\)

Ejercicio\(\PageIndex{40}\)

Ejercicio\(\PageIndex{41}\)

Ejercicio\(\PageIndex{42}\)

Ejercicio\(\PageIndex{43}\)

Ejercicio\(\PageIndex{44}\)

Ejercicio\(\PageIndex{45}\)

Ejercicio\(\PageIndex{46}\)

Ejercicio\(\PageIndex{47}\)

Ejercicio\(\PageIndex{48}\)

Matemáticas cotidianas

Ejercicio\(\PageIndex{49}\)

Ejercicio\(\PageIndex{50}\)

Ejercicios de escritura

Ejercicio\(\PageIndex{51}\)

Ejercicio\(\PageIndex{52}\)

Autocomprobación