Capítulo 4 Ejercicios de revisión
- Page ID
- 110235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capítulo 4 Ejercicios de revisión
Sistema de coordenadas rectangulares
Trazar puntos en un sistema de coordenadas rectangulares
En los siguientes ejercicios, trazar cada punto en un sistema de coordenadas rectangulares.
- (−1, −5)
- (−3,4)
- (2, −3)
- \(\left(1, \frac{5}{2}\right)\)
- (4,3)
- (−4,3)
- (−4, −3)
- (4, −3)
- Contestar
-
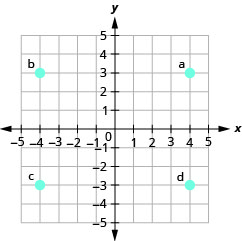
- (−2,0)
- (0, −4)
- (0,5)
- (3,0)
- \(\left(2, \frac{3}{2}\right)\)
- \(\left(3, \frac{4}{3}\right)\)
- \(\left(\frac{1}{3},-4\right)\)
- \(\left(\frac{1}{2},-5\right)\)
- Contestar
-
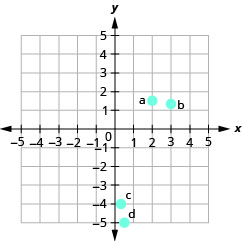
Identificar puntos en una gráfica
En los siguientes ejercicios, nombra el par ordenado de cada punto que se muestra en el sistema de coordenadas rectangulares.
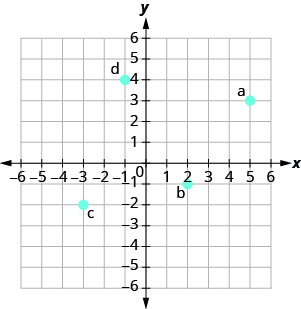
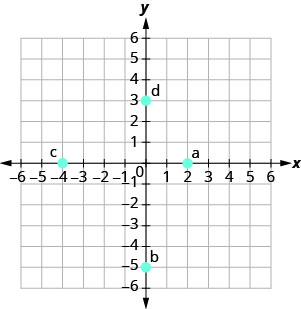
- Contestar
-
a. (2,0)
b (0, −5)
c (−4.0)
d (0,3)
Verificar soluciones a una ecuación en dos variables
En los siguientes ejercicios, ¿qué pares ordenados son soluciones a las ecuaciones dadas?
\(5x+y=10\)
- (5,1)
- (2,0)
- (4, −10)
\(y=6x−2\)
- (1,4)
- \(\left(\frac{1}{3}, 0\right)\)
- (6, −2)
- Contestar
-
1, 2
Completar una Tabla de Soluciones a una Ecuación Lineal en Dos Variables
En los siguientes ejercicios, complete la tabla para encontrar soluciones a cada ecuación lineal.
\(y=4 x-1\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -2 |
\(y=-\frac{1}{2} x+3\)
| x | y | (x, y) |
| 0 | ||
| 4 | ||
| -2 |
- Contestar
-
x y (x, y) 0 3 (0,3) 4 1 (4, 1) −2 4 (−2,4)
\(x+2 y=5\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -1 |
\(3x+2y=6\)
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| -2 |
- Contestar
-
x y (x, y) 0 −3 (0, −3) 2 0 (2,0) −2 −6 (−2, −6)
Encuentre soluciones a una ecuación lineal en dos variables
En los siguientes ejercicios, encuentra tres soluciones para cada ecuación lineal.
\(x+y=3\)
\(x+y=-4\)
- Contestar
-
Las respuestas variarán.
\(y=3 x+1\)
\(y=-x-1\)
- Contestar
-
Las respuestas variarán.
Graficar ecuaciones lineales
Reconocer la relación entre las soluciones de una ecuación y su gráfica
En los siguientes ejercicios, por cada par ordenado, decide:
- ¿El par ordenado es una solución a la ecuación?
- ¿Está el punto en la línea?
\(y=−x+4\)
(0,4) (−1,3)
(2,2) (−2,6)
\(y=\frac{2}{3} x-1\)
\((0,-1) (3,1)\)
\((-3,-3) (6,4)\)
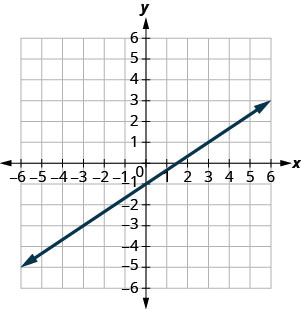
- Contestar
-
- si; si
- sí; no
Graficar una ecuación lineal trazando puntos
En los siguientes ejercicios, grafica por puntos de trazado.
\(y=4x-3\)
\(y=-3x\)
- Contestar
-
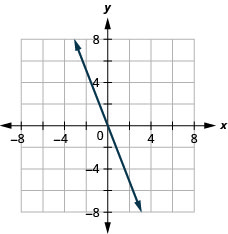
\(y=\frac{1}{2} x+3\)
\(x-y=6\)
- Contestar
-
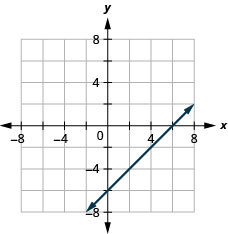
\(2x+y=7\)
\(3x-2y=6\)
- Contestar
-
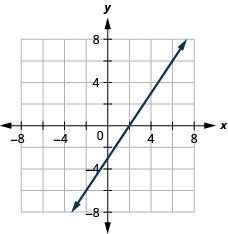
Gráfica líneas verticales y horizontales
En los siguientes ejercicios, grafica cada ecuación.
\(y=-2\)
\(x=3\)
- Contestar
-
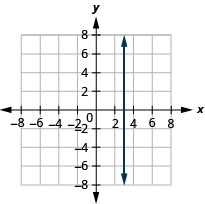
En los siguientes ejercicios, grafica cada par de ecuaciones en un mismo sistema de coordenadas rectangulares.
\(y=-2 x\)y\(y=-2\)
\(y=\frac{4}{3} x\)y\(y=\frac{4}{3}\)
- Contestar
-
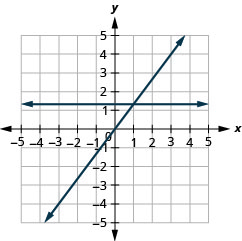
Graficar con intercepciones
Identificar las\(y\) intercepciones\(x\) - y -en una gráfica
En los siguientes ejercicios, encuentra las\(x\) - y\(y\) -intercepciones.
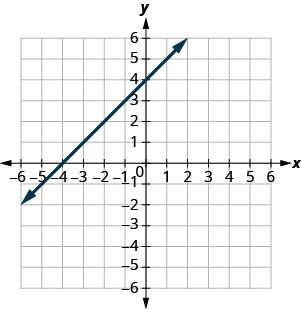
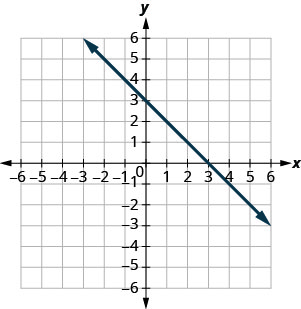
- Contestar
-
\((3,0)\)y\((0,3)\)
Encontrar las\(x\) - y\(y\) -intercepciones a partir de una ecuación de una línea
En los siguientes ejercicios, encuentra las intercepciones de cada ecuación.
\(x+y=5\)
\(x-y=-1\)
- Contestar
-
\((-1,0),(0,1)\)
\(x+2y=6\)
\(2x+3y=12\)
- Contestar
-
\((6,0),(0,4)\)
\(y=\frac{3}{4} x-12\)
\(y=3x\)
- Contestar
-
\((0,0)\)
Graficar una línea usando las intercepciones
En los siguientes ejercicios, grafica usando las intercepciones.
\(-x+3y=3\)
\(x+y=-2\)
- Contestar
-
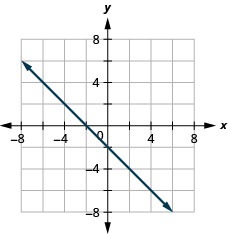
\(x-y=4\)
\(2x-y=5\)
- Contestar
-
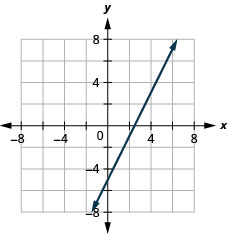
\(2x-4y=8\)
\(y=2x\)
- Contestar
-
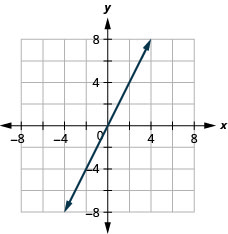
Pendiente de una Línea
Uso de geoplacas para modelar taludes
En los siguientes ejercicios, encuentra la pendiente modelada en cada geobordo.
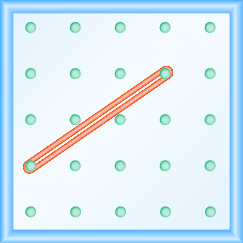
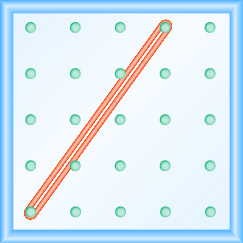
- Contestar
-
\(\frac{4}{3}\)
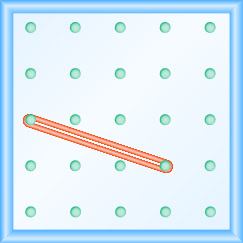
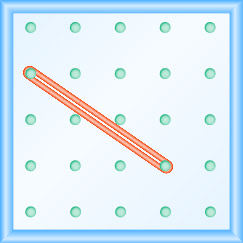
- Contestar
-
\(-\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{3}{2}\)
- Contestar
-
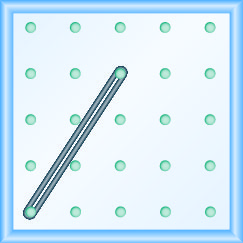
\(-\frac{2}{3}\)
\(-\frac{1}{2}\)
- Contestar
-
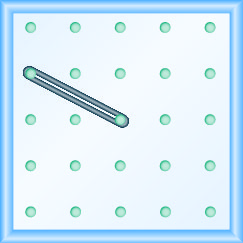
Utilizar\(m=\frac{\text { rise }}{\text { run }}\) para encontrar la Pendiente de una Línea a partir de su Gráfica
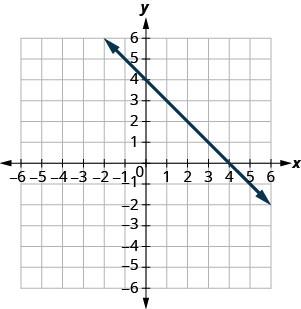
En los siguientes ejercicios, encuentra la pendiente de cada línea mostrada.
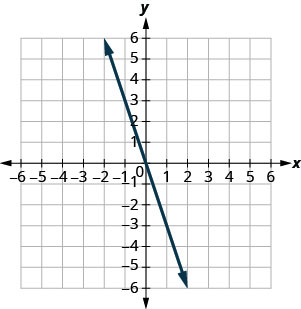
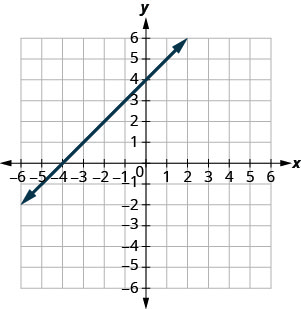
- Contestar
-
1
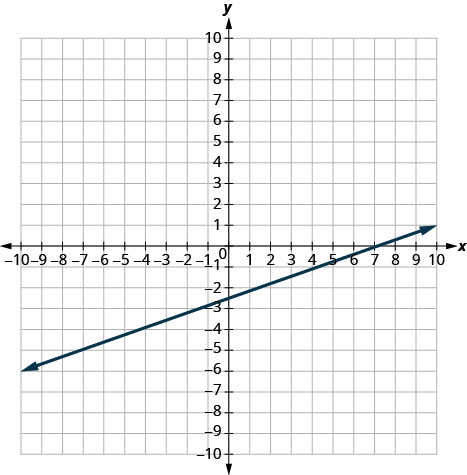
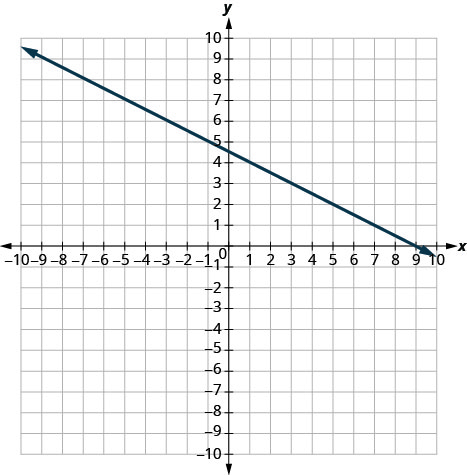
- Contestar
-
\(-\frac{1}{2}\)
Encuentra la Pendiente de Líneas Horizontales y Verticales
En los siguientes ejercicios, encuentra la pendiente de cada línea.
\(y=2\)
\(x=5\)
- Contestar
-
undefined
\(x=-3\)
\(y=-1\)
- Contestar
-
0
Usa la Fórmula de Talud para encontrar la Talud de una Línea entre Dos Puntos
En los siguientes ejercicios, usa la fórmula de pendiente para encontrar la pendiente de la línea entre cada par de puntos.
\((-1,-1),(0,5)\)
\((3,5),(4,-1)\)
- Contestar
-
−6
\((-5,-2),(3,2)\)
\((2,1),(4,6)\)
- Contestar
-
\(\frac{5}{2}\)
Graficar una línea dado un punto y la pendiente
En los siguientes ejercicios, grafica cada línea con el punto y pendiente dados.
\((2,-2) ; \quad m=\frac{5}{2}\)
\((-3,4) ; \quad m=-\frac{1}{3}\)
- Contestar
-
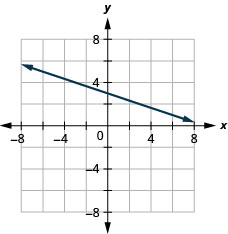
\(x\)-interceptar\(-4 ; \quad m=3\)
\(y\)-interceptar\(1 ; \quad m=-\frac{3}{4}\)
- Contestar
-
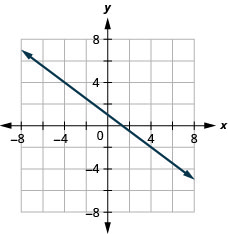
Resolver aplicaciones de pendientes
En los siguientes ejercicios, resuelve estas aplicaciones de taludes.
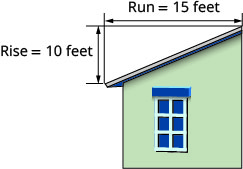
El techo que se muestra a continuación tiene una elevación de\(10\) pies y un recorrido de\(15\) pies. ¿Cuál es su pendiente?
Un camino de montaña se eleva\(50\) pies para una carrera de\(500\) -pie. ¿Cuál es su pendiente?
- Contestar
-
\(\frac{1}{10}\)
Forma de Intercepción de una Ecuación de una Línea
Reconocer la relación entre la gráfica y la forma pendiente-intercepción de una ecuación de una línea
En los siguientes ejercicios, usa la gráfica para encontrar la pendiente y la intercepción y de cada línea. Compara los valores con la ecuación\(y=mx+b\).
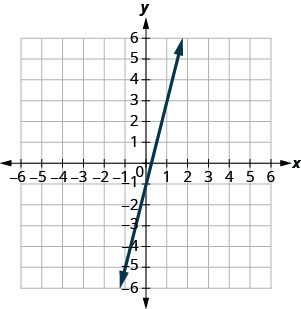
\(y=4x−1\)
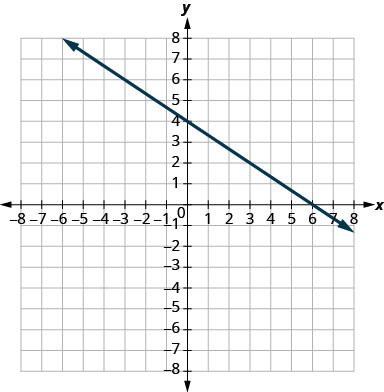
\(y=-\frac{2}{3} x+4\)
- Contestar
-
pendiente\(m=-\frac{2}{3}\) e\(y\) intercepción\((0,4)\)
Identificar la pendiente y la intercepción Y a partir de una ecuación de una línea
En los siguientes ejercicios, identificar la pendiente e\(y\) -intercepción de cada línea.
\(y=-4 x+9\)
\(y=\frac{5}{3} x-6\)
- Contestar
-
\(\frac{5}{3} ;(0,-6)\)
\(5x+y=10\)
\(4x-5y=8\)
- Contestar
-
\(\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)\)
Graficar una línea usando su pendiente e intercepción
En los siguientes ejercicios, grafica la línea de cada ecuación usando su pendiente e\(y\) -intercepción.
\(y=2x+3\)
\(y=-x-1\)
- Contestar
-
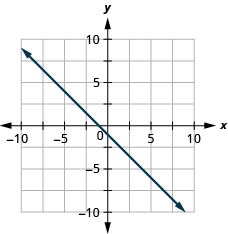
\(y=-\frac{2}{5} x+3\)
\(4x-3y=12\)
- Contestar
-
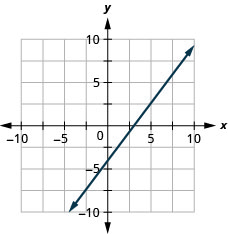
En los siguientes ejercicios, determine el método más conveniente para graficar cada línea.
\(x=5\)
\(y=-3\)
- Contestar
-
línea horizontal
\(2x+y=5\)
\(x-y=2\)
- Contestar
-
intercepta
\(y=x+2\)
\(y=\frac{3}{4} x-1\)
- Contestar
-
trazando puntos
Graficar e interpretar aplicaciones de pendiente—Interceptar
Katherine es chef privada. La ecuación\(C=6.5m+42\) modela la relación entre su costo semanal\(C\),, en dólares y el número de comidas\(m\),, que sirve.
- Encuentra el costo de Katherine por una semana cuando no sirve comidas.
- Encuentra el costo de una semana cuando sirve\(14\) comidas.
- Interpretar la pendiente e\(C\) -intercepción de la ecuación.
- Grafica la ecuación.
Marjorie enseña piano. La ecuación\(P=35h−250\) modela la relación entre su ganancia semanal\(P\),, en dólares y el número de lecciones estudiantiles\(s\),, que imparte.
- Encuentra las ganancias de Marjorie durante una semana cuando no da clases de alumnos.
- Encuentra el beneficio de una semana cuando da clases a los\(20\) estudiantes.
- Interpretar la pendiente e\(P\) -intercepción de la ecuación.
- Grafica la ecuación.
- Contestar
-
- \(−$250\)
- \($450\)
- La pendiente,\(35\), significa que la ganancia semanal de Marjorie,\(P\), aumenta\($35\) por cada lección de estudiante adicional que imparte. El\(P\) -intercepto significa que cuando el número de lecciones es\(0\), Marjorie pierde\($250\).
Usar pendientes para identificar líneas paralelas
En los siguientes ejercicios, utilice pendientes e\(y\) intercepciones para determinar si las líneas son paralelas.
\(4x-3y=-1 ; \quad y=\frac{4}{3} x-3\)
\(2 x-y=8 ; \quad x-2 y=4\)
- Contestar
-
no paralelo
Utilizar pendientes para identificar líneas perpendiculares
En los siguientes ejercicios, use pendientes e intercepciones y para determinar si las líneas son perpendiculares.
\(y=5x-1 ; \quad 10x+2y=0\)
\(3x-2y=5 ; \quad 2x+3y=6\)
- Contestar
-
perpendicular
Encuentra la ecuación de una línea
Encontrar una ecuación de la línea dada la pendiente y -Intercepción
En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente e\(y\) intercepción dadas. Escribe la ecuación en forma de pendiente-intercepción.
pendiente\(\frac{1}{3}\) e\(y\) intercepción\((0,-6)\)
pendiente\(-5\) e\(y\) intercepción\((0,-3)\)
- Contestar
-
\(y=-5x-3\)
pendiente\(0\) e\(y\) intercepción\((0,4)\)
pendiente\(-2\) e\(y\) intercepción\((0,0)\)
- Contestar
-
\(y=-2x\)
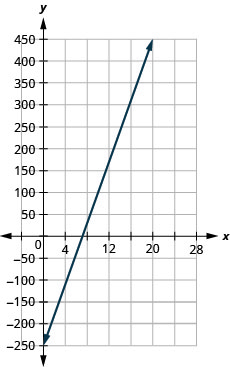
En los siguientes ejercicios, encuentra la ecuación de la línea que se muestra en cada gráfica. Escribe la ecuación en forma de pendiente-intercepción.
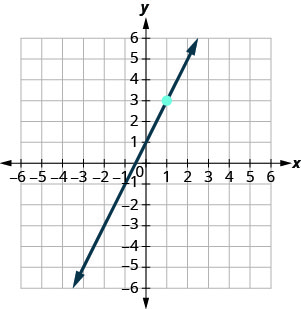
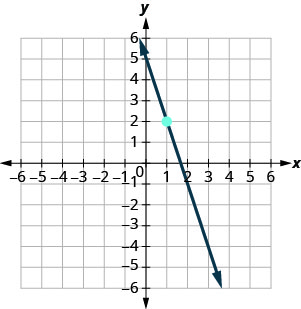
- Contestar
-
\(y=-3x+5\)
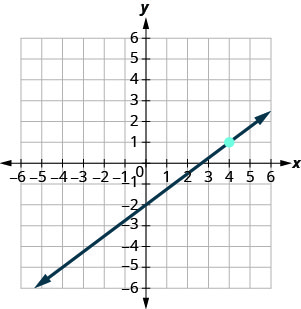
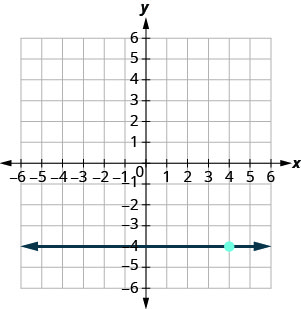
- Contestar
-
\(y=-4\)
Encontrar una ecuación de la línea dada la pendiente y un punto
En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente dada y que contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.
\(m=-\frac{1}{4},\)punto\((-8,3)\)
\(m=\frac{3}{5},\)punto\((10,6)\)
- Contestar
-
\(y=\frac{3}{5} x\)
Línea horizontal que contiene\((-2,7)\)
\(m=-2,\)punto\((-1,-3)\)
- Contestar
-
\(y=-2x-5\)
Encontrar una ecuación de la línea dada dos puntos
En los siguientes ejercicios, encuentra la ecuación de una línea que contiene los puntos dados. Escribe la ecuación en forma de pendiente-intercepción.
\((2,10)\)y\((-2,-2)\)
\((7,1)\)y\((5,0)\)
- Contestar
-
\(y=\frac{1}{2} x-\frac{5}{2}\)
\((3,8)\)y\((3,-4)\)
\((5,2)\)y\((-1,2)\)
- Contestar
-
\(y=2\)
Encontrar una ecuación de una línea paralela a una línea dada
En los siguientes ejercicios, encuentra una ecuación de una línea paralela a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.
\(y=-3x+6,\)punto de línea\((1,-5)\)
\(2x+5y=-10,\)punto de línea\((10,4)\)
- Contestar
-
\(y=-\frac{2}{5} x+8\)
\(x=4,\)punto de línea\((-2,-1)\)
\(y=-5,\)punto de línea\((-4,3)\)
- Contestar
-
\(y=3\)
Encontrar una ecuación de una línea perpendicular a una línea dada
En los siguientes ejercicios, encuentra una ecuación de una línea perpendicular a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.
\(y=-\frac{4}{5} x+2,\)punto de línea\((8,9)\)
\(2x-3y=9,\)punto de línea\((-4,0)\)
- Contestar
-
\(y=-\frac{3}{2} x-6\)
\(y=3,\)punto de línea\((-1,-3)\)
\(x=-5\)punto de línea\((2,1)\)
- Contestar
-
\(y=1\)
Graficar desigualdades lineales
Verificar soluciones a una desigualdad en dos variables
En los siguientes ejercicios, determinar si cada par ordenado es una solución a la desigualdad dada.
Determine si cada par ordenado es una solución a la desigualdad\(y<x−3\):
- \((0,1)\)
- \((−2,−4)\)
- \((5,2)\)
- \((3,−1)\)
- \((−1,−5)\)
Determine si cada par ordenado es una solución a la desigualdad\(x+y>4\):
- \((6,1)\)
- \((−3,6)\)
- \((3,2)\)
- \((−5,10)\)
- \((0,0)\)
- Contestar
-
- si
- no
- si
- si
- no
Reconocer la relación entre las soluciones de una desigualdad y su gráfica
En los siguientes ejercicios, escriba la desigualdad mostrada por la región sombreada.
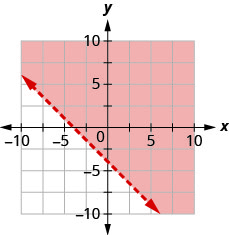
Escribe la desigualdad que muestra la gráfica con la línea límite\(y=−x+2\).
Escribe la desigualdad que muestra la gráfica con la línea de límite\(y=\frac{2}{3} x-3\)
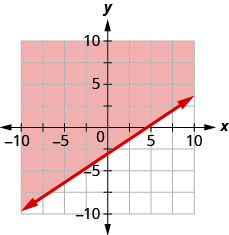
- Contestar
-
\(y>\frac{2}{3} x-3\)
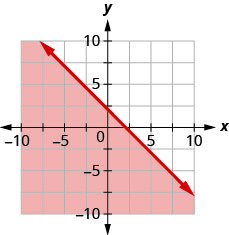
Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite\(x+y=−4\).
Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite\(x−2y=6\).
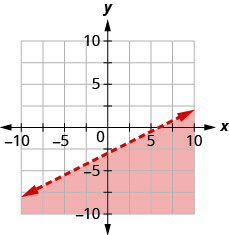
- Contestar
-
\(x-2 y \geq 6\)
Graficar desigualdades lineales
En los siguientes ejercicios, grafica cada desigualdad lineal.
Graficar la desigualdad lineal\(y>\frac{2}{5} x-4\)
Graficar la desigualdad lineal\(y \leq-\frac{1}{4} x+3\)
- Contestar
-
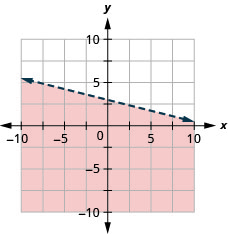
Graficar la desigualdad lineal\(x-y \leq 5\)
Graficar la desigualdad lineal\(3 x+2 y>10\)
- Contestar
-
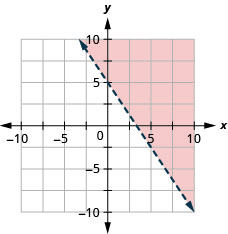
Graficar la desigualdad lineal\(y \leq-3 x\)
Graficar la desigualdad lineal\(y<6\)
- Contestar
-
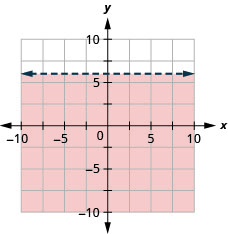
Prueba de práctica
Trazar cada punto en un sistema de coordenadas rectangulares.
- \((2,5)\)
- \((−1,−3)\)
- \((0,2)\)
- \(\left(-4, \frac{3}{2}\right)\)
- \((5,0)\)
¿Cuáles de los pares ordenados dados son soluciones a la ecuación\(3x−y=6\)?
- \((3,3)\)
- \((2,0)\)
- \((4,−6)\)
- Contestar
-
- si
- si
- no
Encuentra tres soluciones a la ecuación lineal\(y=-2x-4\)
Encuentra las\(x\) - y\(y\) -intercepciones de la ecuación\(4x-3y=12\)
- Contestar
-
\((3,0),(0,-4)\)
Encuentra la pendiente de cada línea mostrada.
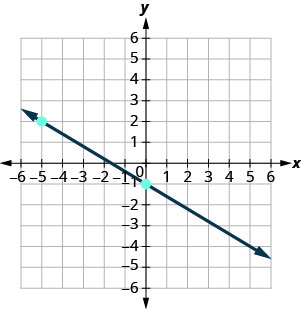
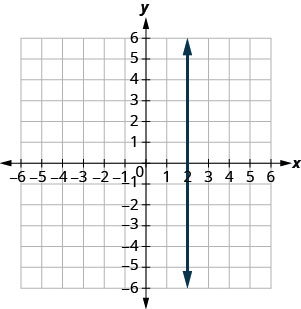
- Contestar
-
undefined
Encuentra la pendiente de la línea entre los puntos\((5,2)\) y\((-1,-4)\)
- Contestar
-
1
Graficar la línea con pendiente\(\frac{1}{2}\) que contiene el punto\((-3,-4)\)
Grafica la línea para cada una de las siguientes ecuaciones.
\(y=\frac{5}{3} x-1\)
- Contestar
-
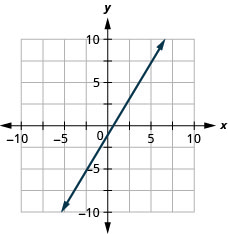
\(y=-x\)
\(x-y=2\)
- Contestar
-
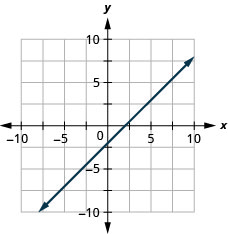
\(4x+2y=-8\)
\(y=2\)
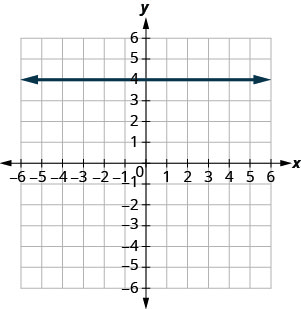
- Contestar
-
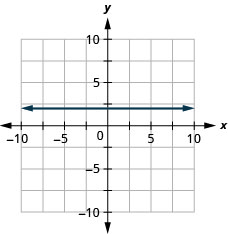
\(x=-3\)
Encuentra la ecuación de cada línea. Escribe la ecuación en forma de pendiente-intercepción.
pendiente\(-\frac{3}{4}\) e\(y\) intercepción\((0,-2)\)
- Contestar
-
\(y=-\frac{3}{4} x-2\)
\(m=2,\)punto\((-3,-1)\)
que contiene\((10,1)\) y\((6,-1)\)
- Contestar
-
\(y=\frac{1}{2} x-4\)
paralelo a la línea\(y=-\frac{2}{3} x-1,\) que contiene el punto\((-3,8)\)
perpendicular a la línea\(y=\frac{5}{4} x+2,\) que contiene el punto\((-10,3)\)
- Contestar
-
\(y=-\frac{4}{5} x-5\)
Escribe la desigualdad que muestra la gráfica con la línea límite\(y=−x−3\).
Grafica cada desigualdad lineal.
\(y>\frac{3}{2} x+5\)
- Contestar
-
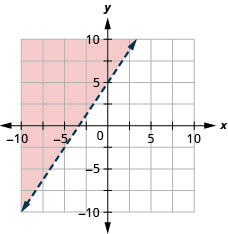
\(x-y \geq-4\)
\(y \leq-5 x\)
- Contestar
-
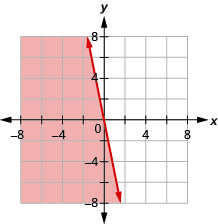
\(y<3\)