6.2: Usar propiedades de multiplicación de exponentes
- Page ID
- 110358
Al final de esta sección, podrás:
- Simplifica expresiones con exponentes
- Simplificar expresiones usando la propiedad de producto para exponentes
- Simplificar expresiones usando la propiedad de potencia para exponentes
- Simplificar expresiones usando la propiedad Product to a Power
- Simplificar expresiones aplicando varias propiedades
- Multiplicar monomios
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(\frac{3}{4}\cdot \frac{3}{4}\)
Si te perdiste este problema, revisa Ejercicio 1.6.13. - Simplificar:\((−2)(−2)(−2)\).
Si te perdiste este problema, revisa Ejercicio 1.5.13.
Simplificar expresiones con exponentes
Recuerda que un exponente indica multiplicación repetida de la misma cantidad. Por ejemplo,\(2^4\) significa el producto de\(4\) factores de\(2\), entonces\(2^4\) significa\(2·2·2·2\).
Revisemos el vocabulario para expresiones con exponentes.
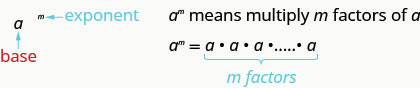
Esto se lee\(a\) al\(m^{th}\) poder.
En la expresión\(a^{m}\), el exponente nos\(m\) dice cuántas veces usamos la base a como factor.

Antes de comenzar a trabajar con expresiones variables que contienen exponentes, simplifiquemos algunas expresiones que involucran solo números.
Simplificar:
- \(4^{3}\)
- \(7^{1}\)
- \(\left(\frac{5}{6}\right)^{2}\)
- \((0.63)^{2}\)
- Responder
-
- \(\begin{array}{ll} & 4^{3}\\ {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\ {\text { Simplify. }} & {64}\end{array}\)
- \(\begin{array}{ll} & 7^{1}\\ \text{Multiply one factor of 7.} & 7\end{array}\)
- \(\begin{array}{ll} &\left(\frac{5}{6}\right)^{2}\\ {\text { Multiply two factors. }} & {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\ {\text { Simplify. }} & {\frac{25}{36}}\end{array}\)
- \(\begin{array}{ll} &(0.63)^{2}\\ {\text { Multiply two factors. }} & {(0.63)(0.63)} \\ {\text { Simplify. }} & {0.3969}\end{array}\)
Simplificar:
- \(6^{3}\)
- \(15^{1}\)
- \(\left(\frac{3}{7}\right)^{2}\)
- \((0.43)^{2}\)
- Responder
-
- 216
- 15
- \(\frac{9}{49}\)
- 0.1849
Simplificar:
- \(2^{5}\)
- \(21^{1}\)
- \(\left(\frac{2}{5}\right)^{3}\)
- \((0.218)^{2}\)
- Responder
-
- 32
- 21
- \(\frac{8}{125}\)
- 0.047524
Simplificar:
- \((-5)^{4}\)
- \(-5^{4}\)
- Responder
-
- \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
- \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)
¡Observe las similitudes y diferencias en el Ejemplo\(\PageIndex{4}\) parte 1 y Ejemplo\(\PageIndex{4}\) parte 2! ¿Por qué son diferentes las respuestas? Al seguir el orden de las operaciones en la parte 1 los paréntesis nos indican elevar el\((−5)\) a la 4ª potencia. En la parte 2 elevamos solo la\(5\) a la 4ª potencia y luego tomamos lo contrario.
Simplificar:
- \((-3)^{4}\)
- \(-3^{4}\)
- Responder
-
- 81
- −81
Simplificar:
- \((-13)^{4}\)
- \(-13^{4}\)
- Responder
-
- 169
- −169
Simplificar expresiones usando la propiedad del producto para exponentes
Has visto que cuando combinas términos similares sumando y restando, necesitas tener la misma base con el mismo exponente. Pero cuando multiplicas y divides, los exponentes pueden ser diferentes, y a veces las bases pueden ser diferentes, también.
Derivaremos las propiedades de los exponentes buscando patrones en varios ejemplos.
Primero, veremos un ejemplo que lleva a la Propiedad del Producto.
 |
|
| ¿Qué significa esto? ¿Cuántos factores en conjunto? |
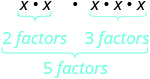 |
| Entonces, tenemos | 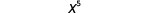 |
| Observe que 5 es la suma de los exponentes, 2 y 3. | 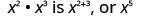 |
Escribimos:\[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]
La base se mantuvo igual y agregamos los exponentes. Esto lleva a la Propiedad del Producto para Exponentes.
Si\(a\) es un número real, y\(m\) y\(n\) están contando números, entonces
\[a^{m} \cdot a^{n}=a^{m+n}\]
Para multiplicar con bases similares, sumar los exponentes.
Un ejemplo con números ayuda a verificar esta propiedad.
\[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]
Simplificar:\(y^{5} \cdot y^{6}\)
- Responder
-
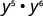
Utilice la propiedad del producto,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Simplificar. 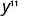
Simplificar:\(b^{9} \cdot b^{8}\)
- Responder
-
\(b^{17}\)
Simplificar:\(x^{12} \cdot x^{4}\)
- Responder
-
\(x^{16}\)
Simplificar:
- \(2^{5} \cdot 2^{9}\)
- \(3\cdot 3^{4}\)
- Responder
-
a.

Utilice la propiedad del producto,\(a^{m} \cdot a^{n}=a^{m+n}\). 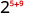
Simplificar. 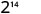
b.
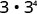
Utilice la propiedad del producto,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Simplificar. 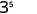
Simplificar:
- \(5\cdot 5^{5}\)
- \(4^{9} \cdot 4^{9}\)
- Responder
-
- \(5^{6}\)
- \(4^{18}\)
Simplificar:
- \(7^{6} \cdot 7^{8}\)
- \(10 \cdot 10^{10}\)
- Responder
-
- \(7^{14}\)
- \(10^{11}\)
Simplificar:
- \(a^{7} \cdot a\)
- \(x^{27} \cdot x^{13}\)
- Responder
-
a.
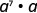
Reescribir,\(a = a^1\) 
Utilice la propiedad del producto,\(a^m\cdot a^n = a^{m+n}\). 
Simplificar. 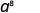
b.

Observe, las bases son las mismas, así que sumar los exponentes. 
Simplificar. 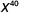
Simplificar:
- \(p^{5} \cdot p\)
- \(y^{14} \cdot y^{29}\)
- Responder
-
- \(p^{6}\)
- \(y^{43}\)
Simplificar:
- \(z \cdot z^{7}\)
- \(b^{15} \cdot b^{34}\)
- Responder
-
- \(z^{8}\)
- \(b^{49}\)
Podemos extender la Propiedad del Producto para Exponentes a más de dos factores.
Simplificar:\(d^{4} \cdot d^{5} \cdot d^{2}\)
- Responder
-
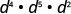
Sumar los exponentes, ya que las bases son las mismas. 
Simplificar. 
Simplificar:\(x^{6} \cdot x^{4} \cdot x^{8}\)
- Responder
-
\(x^{18}\)
Simplificar:\(b^{5} \cdot b^{9} \cdot b^{5}\)
- Responder
-
\(b^{19}\)
Simplificar expresiones mediante la propiedad Power para exponentes
Ahora veamos una expresión exponencial que contiene un poder elevado a un poder. Consulta si puedes descubrir una propiedad general.
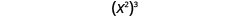 |
|
| ¿Qué significa esto? ¿Cuántos factores en conjunto? |
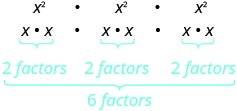 |
| Así que tenemos | 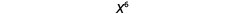 |
| Observe que 6 es producto de los exponentes, 2 y 3. | 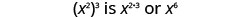 |
Escribimos:
\[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]
Multiplicamos los exponentes. Esto lleva a la Propiedad de Poder para Exponentes.
Si\(a\) es un número real,\(m\) y\(n\) son números enteros, entonces
\[\left(a^{m}\right)^{n}=a^{m \cdot n}\]
Para elevar una potencia a una potencia, multiplicar los exponentes.
Un ejemplo con números ayuda a verificar esta propiedad.
\[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]
Simplificar:
- \(\left(y^{5}\right)^{9}\)
- \(\left(4^{4}\right)^{7}\)
- Responder
-
a.
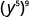
Utilice la propiedad de energía,\(\big(a^m\big)^n = a^{m\cdot n}\). 
Simplificar. 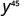
b.
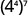
Utilice la propiedad de energía. 
Simplificar. 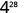
Simplificar:
- \( \left(b^{7}\right)^{5} \)
- \(\left(5^{4}\right)^{3}\)
- Responder
-
- \( b^{35}\)
- \(5^{12}\)
Simplificar:
- \(\left(z^{6}\right)^{9}\)
- \(\left(3^{7}\right)^{7}\)
- Responder
-
- \(z^{54}\)
- \(3^{49}\)
Simplifique las expresiones usando el producto a una propiedad de alimentación
Ahora veremos una expresión que contiene un producto que se eleva a una potencia. ¿Puedes encontrar este patrón?
\(\begin{array}{ll}{\text { What does this mean? }} & {\text { (2x) }^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)
\(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)
¡El exponente aplica a cada uno de los factores! Esto lleva al Producto a una Propiedad de Potencia para Exponentes.
Si\(a\) y\(b\) son números reales y\(m\) es un número entero, entonces
\[(a b)^{m}=a^{m} b^{m}\]
Para elevar un producto a una potencia, elevar cada factor a esa potencia.
Un ejemplo con números ayuda a verificar esta propiedad:
\ [\ begin {array} {lll} (2\ cdot 3) ^ {2} &\ stackrel {?} {=} &2^ {2}\ cdot 3^ {2}\\ 6^ {2} &\ stackrel {?} {=} &4\ cdot 9\\ 36 &=&36
\ marca de verificación\ end {array}\]
Simplificar:
- \((-9 d)^{2}\)
- \((3mn)^{3}\).
- Responder
-
a.
b.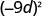
Poder de Uso de una Propiedad de Producto,\((ab)^m=a^m b^m\). 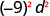
Simplificar. 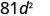
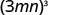
Poder de Uso de una Propiedad de Producto,\((ab)^m=a^m b^m\). 
Simplificar. 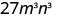
Simplificar:
- \((-12 y)^{2}\)
- \((2 w x)^{5}\)
- Responder
-
- \(144y^{2}\)
- \(32w^{5} x^{5}\)
Simplificar:
- \((5 w x)^{3}\)
- \((-3 y)^{3}\)
- Responder
-
- 125\(w^{3} x^{3}\)
- \(-27 y^{3}\)
Simplificar expresiones mediante la aplicación de varias propiedades
Ahora tenemos tres propiedades para multiplicar expresiones con exponentes. Vamos a resumirlos y luego haremos algunos ejemplos que utilizan más de una de las propiedades.
Si\(a\) y\(b\) son números reales, y\(m\) y\(n\) son números enteros, entonces
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
Todas las propiedades de exponente son verdaderas para cualquier número real\(m\) y\(n\). Ahora mismo, solo usamos exponentes de números enteros.
Simplificar:
- \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
- \(\left(-6 x^{4} y^{5}\right)^{2}\)
- Responder
-
- \(\begin{array}{ll}& \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\ {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\ {\text { Add the exponents. }} & y^{38} \end{array}\)
- \(\begin{array}{ll}& \left(-6 x^{4} y^{5}\right)^{2}\\ {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\ {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\ {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
Simplificar:
- \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
- \(\left(-2 c^{4} d^{2}\right)^{3}\)
- Contestar
-
- \(a^{48}\)
- \(-8 c^{12} d^{6}\)
Simplificar:
- \(\left(-3 x^{6} y^{7}\right)^{4}\)
- \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
- Contestar
-
- 81\(x^{24} y^{28}\)
- \(q^{29}\)
Simplificar:
- \((5 m)^{2}\left(3 m^{3}\right)\)
- \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
- Contestar
-
- \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
- \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
Simplificar:
- \((5 n)^{2}\left(3 n^{10}\right)\)
- \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
- Contestar
-
- 75\(n^{12}\)
- 81\(c^{24} d^{30}\)
Simplificar:
- \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
- \((2 x)^{3}\left(5 x^{7}\right)\)
- Contestar
-
- 256\(a^{22} b^{24}\)
- 40\(x^{10}\)
Multiplicar monomios
Dado que un monomio es una expresión algebraica, podemos usar las propiedades de los exponentes para multiplicar los monomios.
Multiplicar:\(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)
- Contestar
-
\ (\ begin {array} {ll} &\ left (3 x^ {2}\ right)\ left (-4 x^ {3}\ right)\\ text {Usa la propiedad conmutativa para reorganizar los términos.} & 3\ cdot (-4)\ cdot x^ {2}\ cdot x^ {3}\\
\ texto {Multiplicar.} & -12 x^ {5}\ end {array}\)
Multiplicar:\(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)
- Contestar
-
\(-35 y^{11}\)
Multiplicar:\(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)
- Contestar
-
54\(b^{9}\)
Multiplicar:\(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)
- Contestar
-
\(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)
Multiplicar:\(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)
- Contestar
-
6\(a^{5} b^{6}\)
Multiplicar:\(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)
- Contestar
-
8\(r^{11} s^{8}\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con el uso de propiedades de multiplicación de exponentes:
- Propiedades de multiplicación de exponentes
Conceptos clave
- Notación exponencial
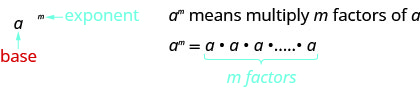
- Propiedades de los Exponentes
- Si\(a\) y\(b\) son números reales y\(m\) y\(n\) son números enteros, entonces
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]


