6.4: Productos especiales
- Page ID
- 110390
Al final de esta sección, podrás:
- Cuadrando un binomio usando el Patrón de Cuadrados Binomiales
- Multiplicar conjugados usando el Patrón de Producto de Conconjugados
- Reconocer y utilizar el patrón de producto especial apropiado
Antes de comenzar, toma este cuestionario de preparación.
Simplificar: a.\(9^2\) b.\((−9)^2\)\(−9^2\) c.
Si te perdiste este problema, revisa Ejercicio 1.5.13.
Cuadrando un Binomial Usando el Patrón de Cuadrados Binomiales
A los matemáticos les gusta buscar patrones que faciliten su trabajo. Un buen ejemplo de esto es la cuadratura de binomios. Si bien siempre puedes obtener el producto escribiendo el binomio dos veces y usando los métodos de la última sección, hay menos trabajo por hacer si aprendes a usar un patrón.
\[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]
Mira estos resultados. ¿Ves algún patrón?
¿Qué pasa con el número de términos? En cada ejemplo cuadrábamos un binomio y el resultado fue un trinomio.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]
Ahora mira el primer término en cada resultado. ¿De dónde vino?
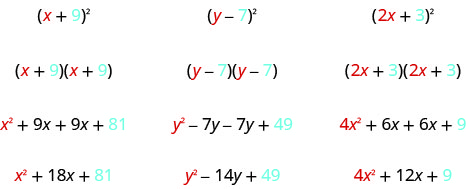
El primer término es producto de los primeros términos de cada binomio. Como los binomios son idénticos, ¡es solo el cuadrado del primer término!
\[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]
Para obtener el primer término del producto, cuadrar el primer término.
¿De dónde vino el último término? Mira los ejemplos y encuentra el patrón.
El último término es producto de los últimos términos, que es el cuadrado del último término.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]
Para obtener el último término del producto, cuadrar el último término.
Por último, mira el término medio. Observe que vino de agregar los términos “exterior” e “interno”, ¡que son ambos iguales! Entonces el término medio es el doble del producto de los dos términos del binomio.
\[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]
\[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]
Para obtener el término medio del producto, multiplique los términos y duplique su producto.
Poniéndolo todo junto:
Si\(a\) y\(b\) son números reales, el patrón cuadrado binomial es
\[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2} + \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]
Aplicando esto a dos tipos binomiales:
\[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]
Para cuadrar un binomio:
- cuadrar el primer término
- cuadrar el último término
- duplicar su producto
Un ejemplo numérico ayuda a verificar el patrón.
\(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)
Para multiplicar\((10+4)^2\) normalmente seguirías el Orden de Operaciones.
\[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]
¡El patrón funciona!
\(\text { Multiply: }(x+5)^{2}\)
Solución:
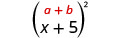 |
|
| Cuadrado el primer término. |  |
| Cuadrarse el último término. |  |
| Duplique el producto. |  |
| Simplificar. | \(x^{2}+10 x+25\) |
Multiplicar:\((x+9)^{2}\)
- Responder
-
\(x^{2}+18 x+81\)
Multiplicar:\((y+11)^{2}\)
- Responder
-
\(y^{2}+22 y+121\)
Multiplicar:\((y-3)^{2}\)
Solución:
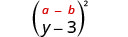 |
|
| Cuadrado el primer término. |  |
| Cuadrarse el último término. |  |
| Duplique el producto. | 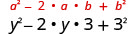 |
| Simplificar. | \(y^{2}-6 y+9\) |
Multiplicar:\((x-9)^{2}\)
- Responder
-
\(x^{2}-18 x+81\)
Multiplicar:\((p-13)^{2}\)
- Responder
-
\(p^{2}-26 p+169\)
Multiplicar:\((4 x+6)^{2}\)
Solución:
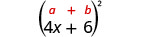 |
|
| Usa el patrón. | 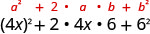 |
| Simplificar. | \(16 x^{2}+48 x+36\) |
Multiplicar:\((6 x+3)^{2}\)
- Responder
-
\(36 x^{2}+36 x+9\)
Multiplicar:\((4 x+9)^{2}\)
- Responder
-
\(16 x^{2}+72 x+81\)
Multiplicar:\((2 x-3 y)^{2}\)
Solución:
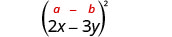 |
|
| Usa el patrón. | 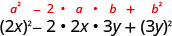 |
| Simplificar. | \(4 x^{2}-12 x y+9 y^{2}\) |
Multiplicar:\((2 c-d)^{2}\)
- Responder
-
\(4 c^{2}-4 c d+d^{2}\)
Multiplicar:\((4 x-5 y)^{2}\)
- Responder
-
\(16 x^{2}-40 x y+25 y^{2}\)
Multiplicar:\(\left(4 u^{3}+1\right)^{2}\)
Solución:
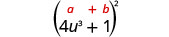 |
|
| Usa el patrón. | 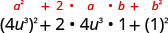 |
| Simplificar. | \(16 u^{6}+8 u^{3}+1\) |
Multiplicar:\(\left(2 x^{2}+1\right)^{2}\)
- Responder
-
\(4 x^{4}+4 x^{2}+1\)
Multiplicar:\(\left(3 y^{3}+2\right)^{2}\)
- Responder
-
\(9 y^{6}+12 y^{3}+4\)
Multiplicar conjugados usando el producto del patrón de conjugados
Acabamos de ver un patrón para cuadrar binomios que podemos usar para facilitar la multiplicación de algunos binomios. De igual manera, existe un patrón para otro producto de binomios. Pero antes de llegar a ello, necesitamos introducir algo de vocabulario.
¿Qué notas de estos pares de binomios?
\[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]
Mira el primer término de cada binomio en cada par.
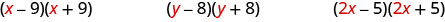
Observe que los primeros términos son los mismos en cada par.
Mira los últimos términos de cada binomio en cada par.
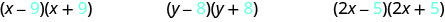
Observe que los últimos términos son los mismos en cada par.
Observe cómo cada par tiene una suma y una diferencia.
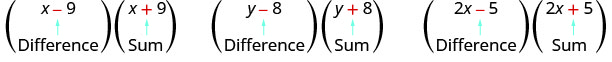
Un par de binomios que tienen cada uno el mismo primer término y el mismo último término, pero uno es una suma y otro es una diferencia tiene un nombre especial. Se llama par conjugado y es de la forma (a−b), (a+b).
Un par conjugado es dos binomios de la forma
\[(a-b),(a+b)\nonumber \]
El par de binomios tienen cada uno el mismo primer término y el mismo último término, pero un binomio es una suma y el otro es una diferencia.
Hay un patrón agradable para encontrar el producto de los conjugados. Podrías, por supuesto, simplemente FOIL para obtener el producto, pero usar el patrón facilita tu trabajo.
Busquemos el patrón usando FOIL para multiplicar algunos pares conjugados.
\[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]
Cada primer término es producto de los primeros términos de los binomios, y como son idénticos es el cuadrado del primer término.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]
El último término vino de multiplicar los últimos términos, el cuadrado del último término.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]
¿Qué observas de los productos?
¡El producto de los dos binomios también es un binomio! La mayoría de los productos resultantes de FOIL han sido trinomios.
¿Por qué no hay término medio? Observe los dos términos medios que obtiene de FOIL combinan a 0 en cada caso, el resultado de una suma y una resta.
El producto de los conjugados es siempre de la forma\(a^2-b^2\). Esto se llama diferencia de cuadrados.
Esto lleva al patrón:
Si\(a\) y\(b\) son números reales,

El producto se llama diferencia de cuadrados.
Para multiplicar conjugados, cuadrar el primer término, cuadrar el último término y escribir el producto como una diferencia de cuadrados.
Probemos este patrón con un ejemplo numérico.
\(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)
Fíjate, ¡el resultado es el mismo!
Multiplicar:\((x-8)(x+8)\)
Solución:
Primero, reconozca esto como un producto de conjugados. Los binomios tienen los mismos primeros términos, y los mismos últimos términos, y un binomio es una suma y el otro es una diferencia.
| Se ajusta al patrón. | 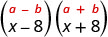 |
| Cuadrar el primer término, x. | 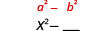 |
| Cuadrado el último término, 8. | 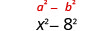 |
| El producto es una diferencia de cuadrados. | 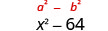 |
Multiplicar:\((x-5)(x+5)\)
- Responder
-
\(x^{2}-25\)
Multiplicar:\((w-3)(w+3)\)
- Responder
-
\(w^{2}-9\)
Multiplicar:\((2 x+5)(2 x-5)\)
Solución:
¿Los binomios son conjugados?
| Es producto de conjugados. | 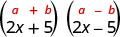 |
| Cuadrar el primer término, 2 x. | 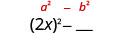 |
| Cuadrarse el último término, 5. | 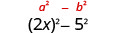 |
| Simplificar. El producto es una diferencia de cuadrados. | 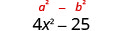 |
Multiplicar:\((6 x+5)(6 x-5)\)
- Responder
-
\(36 x^{2}-25\)
Multiplicar:\((2 x+7)(2 x-7)\)
- Responder
-
\(4 x^{2}-49\)
Los binomios en el siguiente ejemplo pueden mirar hacia atrás — la variable está en el segundo término. Pero los dos binomios siguen siendo conjugados, así que usamos el mismo patrón para multiplicarlos.
Encuentra el producto:\((3+5 x)(3-5 x)\)
Solución:
| Es producto de conjugados. | 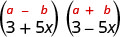 |
| Usa el patrón. | 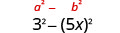 |
| Simplificar. | \(9-25 x^{2}\) |
Multiplicar:\((7+4 x)(7-4 x)\)
- Responder
-
\(49-16 x^{2}\)
Multiplicar:\((9-2 y)(9+2 y)\)
- Responder
-
\(81-4 y^{2}\)
Ahora vamos a multiplicar los conjugados que tienen dos variables.
Encuentra el producto:\((5 m-9 n)(5 m+9 n)\)
Solución:
| Esto se ajusta al patrón. | 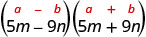 |
| Usa el patrón. | 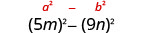 |
| Simplificar. | \(25 m^{2}-81 n^{2}\) |
Encuentra el producto:\((4 p-7 q)(4 p+7 q)\)
- Responder
-
\(16 p^{2}-49 q^{2}\)
Encuentra el producto:\((3 x-y)(3 x+y)\)
- Responder
-
\(9 x^{2}-y^{2}\)
Encuentra el producto:\((c d-8)(c d+8)\)
Solución:
| Esto se ajusta al patrón. | 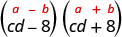 |
| Usa el patrón. | 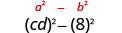 |
| Simplificar. | \(c^{2} d^{2}-64\) |
Encuentra el producto:\((x y-6)(x y+6)\)
- Responder
-
\(x^{2} y^{2}-36\)
Encuentra el producto:\((a b-9)(a b+9)\)
- Responder
-
\(a^{2} b^{2}-81\)
Encuentra el producto:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)
Solución:
| Esto se ajusta al patrón. | 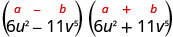 |
| Usa el patrón. | 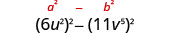 |
| Simplificar. | \(36 u^{4}-121 v^{10}\) |
Encuentra el producto:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)
- Responder
-
\(9 x^{4}-16 y^{6}\)
Encuentra el producto:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)
- Responder
-
\(4 m^{4}-25 n^{6}\)
Reconocer y utilizar el patrón de producto especial apropiado
Acabamos de desarrollar patrones especiales de productos para Cuadrados Binomiales y para el Producto de Conconjugados. Los productos se ven similares, por lo que es importante reconocer cuándo es apropiado usar cada uno de estos patrones y notar en qué se diferencian. Mira los dos patrones juntos y anota sus similitudes y diferencias.
\(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)
Elige el patrón adecuado y úsalo para encontrar el producto:
- \((2 x-3)(2 x+3)\)
- \((8 x-5)^{2}\)
- \((6 m+7)^{2}\)
- \((5 x-6)(6 x+5)\)
Solución:
1. \((2x−3)(2x+3)\)Estos son conjugados. Tienen los mismos primeros números, y los mismos últimos números, y un binomio es una suma y el otro es una diferencia. Se ajusta al patrón Producto de Conjugados.
| Esto se ajusta al patrón. | 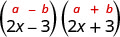 |
| Usa el patrón. | 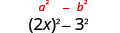 |
| Simplificar. | \(4 x^{2}-9\) |
2. \((8 x-5)^{2}\)Se nos pide cuadrar un binomio. Se ajusta al patrón de cuadrados binomiales.
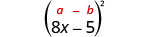 |
|
| Usa el patrón. |  |
| Simplificar. | \(64 x^{2}-80 x+25\) |
3. \((6 m+7)^{2}\)Nuevamente, cuadraremos un binomio así que usaremos el patrón de cuadrados binomiales.
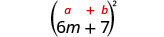 |
|
| Usa el patrón. |  |
| Simplificar. | \(36 m^{2}+84 m+49\) |
4. \((5 x-6)(6 x+5)\)Este producto no se ajusta a los patrones, por lo que usaremos FOIL.
\(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)
Elige el patrón adecuado y úsalo para encontrar el producto:
- \((9b−2)(2b+9)\)
- \((9p−4)2\)
- \((7y+1)^2\)
- \((4r-3)(4r+3)\)
- Responder
-
- FOIL;\(18 b^{2}+77 b-18\)
- Cuadrados Binomiales;\(81 p^{2}-72 p+16\)
- Cuadrados Binomiales;\(49 y^{2}+14 y+1\)
- Producto de Conjugados;\(16 r^{2}-9\)
Elige el patrón adecuado y úsalo para encontrar el producto:
- \((6x+7)^2\)
- \((3x−4)(3x+4)\)
- \((2x−5)(5x−2)\)
- \((6n−1)^2\)
- Responder
-
- Cuadrados Binomiales;\(36 x^{2}+84 x+49\)
- Producto de Conjugados;\(9 x^{2}-16\)
- FOIL;\(10 x^{2}-29 x+10\)
- Cuadrados Binomiales;\(36 n^{2}-12 n+1\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con productos especiales:
- Productos Especiales
Conceptos clave
- Patrón Cuadrados Binomiales
- Si a, b son números reales,
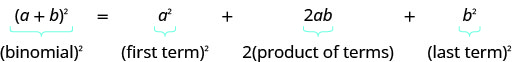
- \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
- \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
- Para cuadrar un binomio: cuadrar el primer término, cuadrar el último término, duplicar su producto.
- Si a, b son números reales,
- Producto del patrón de conjugados
- Si a, ba, b son números reales,
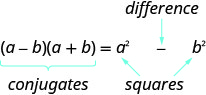
- \((a-b)(a+b)=a^{2}-b^{2}\)
- El producto se llama diferencia de cuadrados.
- Si a, ba, b son números reales,
- Para multiplicar conjugados:
- cuadrado el primer término cuadrado el último término escríbelo como una diferencia de cuadrados
Glosario
- par conjugado
- Un par conjugado es dos binomios de la forma\((a−b)\) y\((a+b)\); el par de binomios cada uno tiene el mismo primer término y el mismo último término, pero un binomio es una suma y el otro es una diferencia.


