6.3E: Ejercicios
- Page ID
- 110383
La práctica hace la perfección
Multiplicar un polinomio por un monomio
En los siguientes ejercicios, multiplicar.
4\((w+10)\)
- Contestar
-
4w+40
6 (b+8)
−3 (a+7)
- Contestar
-
−3a−21
−5 (p+9)
2 (x−7)
- Contestar
-
2x−14
7 (y−4)
−3 (k−4)
- Contestar
-
−3k+12
−8 (j−5)
q (q+5)
- Contestar
-
\(q^{2}+5 q\)
k (k+7)
−b (b+9)
- Contestar
-
\(-b^{2}-9 b\)
−y (y+3)
−x (x−10)
- Contestar
-
\(-x^{2}+10 x\)
−p (p−15)
6r (4r+s)
- Contestar
-
\(24 r^{2}+6 r s\)
5c (9c+d)
12x (x−10)
- Contestar
-
\(12 x^{2}-120 x\)
9m (m−11)
−9a (3a+5)
- Contestar
-
\(-27 a^{2}-45 a\)
−4p (2p+7)
3\(\left(p^{2}+10 p+25\right)\)
- Contestar
-
\(3 p^{2}+30 p+75\)
6\(\left(y^{2}+8 y+16\right)\)
\(-8 x\left(x^{2}+2 x-15\right)\)
- Contestar
-
\(-8 x^{3}-16 x^{2}+120 x\)
\(-5 t\left(t^{2}+3 t-18\right)\)
5\(q^{3}\left(q^{3}-2 q+6\right)\)
- Contestar
-
\(5 q^{6}-10 q^{4}+30 q^{3}\)
4\(x^{3}\left(x^{4}-3 x+7\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Contestar
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Contestar
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Contestar
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 m-9) m\)
- Contestar
-
\(2 m^{2}-9 m\)
\((8 j-1) j\)
\((w-6) \cdot 8\)
- Contestar
-
\(8 w-48\)
\((k-4) \cdot 5\)
4\((x+10)\)
- Contestar
-
4x+40
6 (y+8)
15 (r−24)
- Contestar
-
15r−360
12 (v−30)
−3 (m+11)
- Contestar
-
−3m−33
−4 (p+15)
−8 (z−5)
- Contestar
-
−8z+40
−3 (x−9)
u (u+5)
- Contestar
-
\(u^{2}+5 u\)
\(q(q+7)\)
\(n\left(n^{2}-3 n\right)\)
- Contestar
-
\(n^{3}-3 n^{2}\)
\(s\left(s^{2}-6 s\right)\)
6\(x(4 x+y)\)
- Contestar
-
\(24 x^{2}+6 x y\)
5a (9a+b)
5p (11p−5q)
- Contestar
-
\(55 p^{2}-25 p q\)
12\(u(3 u-4 v)\)
3\(\left(v^{2}+10 v+25\right)\)
- Contestar
-
\(3 v^{2}+30 v+75\)
6\(\left(x^{2}+8 x+16\right)\)
2\(n\left(4 n^{2}-4 n+1\right)\)
- Contestar
-
\(8 n^{3}-8 n^{2}+2 n\)
3\(r\left(2 r^{2}-6 r+2\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Contestar
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Contestar
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Contestar
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 y-9) y\)
- Contestar
-
\(18 y^{2}-9 y\)
\((8 b-1) b\)
Multiplicar un Binomio por un Binomio
En los siguientes ejercicios, multiplique los siguientes binomios usando: ⓐ la Propiedad Distributiva ⓑ el método FOIL ⓒ el Método Vertical.
(w+5) (w+7)
- Contestar
-
\(w^{2}+12 w+35\)
(y+9) (y+3)
(p+11) (p−4)
- Contestar
-
\(p^{2}+7 p-44\)
(q+4) (q−8)
En los siguientes ejercicios, multiplique los binomios. Utilice cualquier método.
(x+8) (x+3)
- Contestar
-
\(x^{2}+11 x+24\)
(y+7) (y+4)
(y−6) (y−2)
- Contestar
-
\(y^{2}-8 y+12\)
(x−7) (x−2)
(w−4) (w+7)
- Contestar
-
\(w^{2}+3 w-28\)
\((q-5)(q+8)\)
(p+12) (p−5)
- Contestar
-
\(p^{2}+7 p-60\)
(m+11) (m−4)
(6p+5) (p+1)
- Contestar
-
\(6 p^{2}+11 p+5\)
\((7 m+1)(m+3)\)
(2t−9) (10t+1)
- Contestar
-
\(20 t^{2}-88 t-9\)
(3r−8) (11r+1)
(5x−y) (3x−6)
- Contestar
-
\(15 x^{2}-3 x y-30 x+6 y\)
(10a−b) (3a−4)
(a+b) (2a+3b)
- Contestar
-
\(2 a^{2}+5 a b+3 b^{2}\)
(r+s) (3r+2s)
(4z−y) (z−6)
- Contestar
-
\(4 z^{2}-24 z-z y+6 y\)
(5x−y) (x−4)
\(\left(x^{2}+3\right)(x+2)\)
- Contestar
-
\(x^{3}+2 x^{2}+3 x+6\)
\(\left(y^{2}-4\right)(y+3)\)
\(\left(x^{2}+8\right)\left(x^{2}-5\right)\)
- Contestar
-
\(x^{4}+3 x^{2}-40\)
\(\left(y^{2}-7\right)\left(y^{2}-4\right)\)
(5ab−1) (2ab+3)
- Contestar
-
\(10 a^{2} b^{2}+13 a b-3\)
(2xy+3) (3xy+2)
(6pq−3) (4pq−5)
- Contestar
-
\(24 p^{2} q^{2}-42 p q+15\)
(3rs−7) (3rs−4)
Multiplicar un Trinomio por un Binomio
En los siguientes ejercicios, multiplique usando ⓐ la Propiedad Distributiva ⓑ el Método Vertical.
\((x+5)\left(x^{2}+4 x+3\right)\)
- Contestar
-
\(x^{3}+9 x^{2}+23 x+15\)
\((u+4)\left(u^{2}+3 u+2\right)\)
\((y+8)\left(4 y^{2}+y-7\right)\)
- Contestar
-
\(4 y^{3}+33 y^{2}+y-56\)
\((a+10)\left(3 a^{2}+a-5\right)\)
En los siguientes ejercicios, multiplicar. Utilice cualquiera de los dos métodos.
\((w-7)\left(w^{2}-9 w+10\right)\)
- Contestar
-
\(w^{3}-16 w^{2}+73 w-70\)
\((p-4)\left(p^{2}-6 p+9\right)\)
\((3 q+1)\left(q^{2}-4 q-5\right)\)
- Contestar
-
\(3 q^{3}-11 q^{2}-19 q-5\)
\((6 r+1)\left(r^{2}-7 r-9\right)\)
Práctica Mixta
(10y−6) + (4y−7)
- Contestar
-
14y−13
(15p−4) + (3p−5)
\(\left(x^{2}-4 x-34\right)-\left(x^{2}+7 x-6\right)\)
- Contestar
-
−11x−28
\(\left(j^{2}-8 j-27\right)-\left(j^{2}+2 j-12\right)\)
5\(q\left(3 q^{2}-6 q+11\right)\)
- Contestar
-
\(15 q^{3}-30 q^{2}+55 q\)
8\(t\left(2 t^{2}-5 t+6\right)\)
(s−7) (s+9)
- Contestar
-
\(s^{2}+2 s-63\)
(x−5) (x+13)
\(\left(y^{2}-2 y\right)(y+1)\)
- Contestar
-
\(y^{3}-y^{2}-2 y\)
\(\left(a^{2}-3 a\right)(4 a+5)\)
\((3 n-4)\left(n^{2}+n-7\right)\)
- Contestar
-
\(3 n^{3}-n^{2}-25 n+28\)
\((6 k-1)\left(k^{2}+2 k-4\right)\)
\((7 p+10)(7 p-10)\)
- Contestar
-
\(49 p^{2}-100\)
(3y+8) (3y−8)
\(\left(4 m^{2}-3 m-7\right) m^{2}\)
- Contestar
-
\(4 m^{4}-3 m^{3}-7 m^{2}\)
\(\left(15 c^{2}-4 c+5\right) c^{4}\)
\((5 a+7 b)(5 a+7 b)\)
- Contestar
-
\(25 a^{2}+70 a b+49 b^{2}\)
(3x−11y) (3x−11y)
(4y+12z) (4y−12z)
- Contestar
-
\(16 y^{2}-144 z^{2}\)
Matemáticas cotidianas
Matemáticas mentales Se puede utilizar la multiplicación binomial para multiplicar números sin una calculadora. Digamos que necesitas multiplicar 13 veces 15. Piense en 13 como 10+3 y 15 como 10+5.
- Multiplica (10+3) (10+5) por el método FOIL.
- Multiplica 13·15 sin usar una calculadora.
- ¿Cuál es la manera más fácil para ti? ¿Por qué?
Matemáticas mentales Se puede utilizar la multiplicación binomial para multiplicar números sin una calculadora. Digamos que necesitas multiplicar 18 veces 17. Piense en 18 como 20−2 y 17 como 20−3.
- Multiplica (20−2) (20−3) por el método FOIL.
- Multiplica 18·17 sin usar una calculadora.
- ¿Cuál es la manera más fácil para ti? ¿Por qué?
- Contestar
-
- 306
- 306
- Las respuestas variarán.
Ejercicios de escritura
¿Qué método prefieres usar al multiplicar dos binomios: la Propiedad Distributiva, el método FOIL o el Método Vertical? ¿Por qué?
¿Qué método prefieres usar al multiplicar un trinomio por un binomio: la Propiedad Distributiva o el Método Vertical? ¿Por qué?
- Contestar
-
Las respuestas variarán.
Multiplica lo siguiente:
\(\begin{array}{l}{(x+2)(x-2)} \\ {(y+7)(y-7)} \\ {(w+5)(w-5)}\end{array}\)
Explica el patrón que ves en tus respuestas.
Multiplica lo siguiente:
\(\begin{array}{l}{(m-3)(m+3)} \\ {(n-10)(n+10)} \\ {(p-8)(p+8)}\end{array}\)
Explica el patrón que ves en tus respuestas.
- Contestar
-
Las respuestas pueden variar.
Multiplica lo siguiente:
\(\begin{array}{l}{(p+3)(p+3)} \\ {(q+6)(q+6)} \\ {(r+1)(r+1)}\end{array}\)
Explica el patrón que ves en tus respuestas.
Multiplica lo siguiente:
\(\begin{array}{l}{(x-4)(x-4)} \\ {(y-1)(y-1)} \\ {(z-7)(z-7)}\end{array}\)
Explica el patrón que ves en tus respuestas.
- Contestar
-
Las respuestas pueden variar.
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
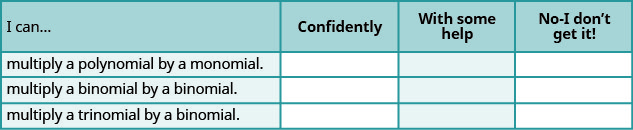
b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?