9.6: Resolver ecuaciones con raíces cuadradas
- Page ID
- 110176
Al final de esta sección, podrás:
- Resolver ecuaciones radicales
- Uso de raíces cuadradas en aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar: ⓐ\(\sqrt{9}\) ⓑ\(9^2\).
Si te perdiste este problema, revisa el Ejemplo 9.1.1 y el Ejercicio 1.3.22. - Resolver: 5 (x+1) −4=3 (2x−7).
Si te perdiste este problema, revisa el Ejercicio 2.4.16. - Resolver:\(n^2−6n+8=0\).
Si te perdiste este problema, revisa el Ejercicio 7.6.13.
Resolver ecuaciones radicales
En esta sección resolveremos ecuaciones que tienen la variable en el radicando de una raíz cuadrada. Las ecuaciones de este tipo se denominan ecuaciones radicales.
Una ecuación en la que la variable está en el radicando de una raíz cuadrada se denomina ecuación radical.
Como es habitual, al resolver estas ecuaciones, lo que hacemos a un lado de una ecuación debemos hacer también al otro lado. Dado que cuadrar una cantidad y tomar una raíz cuadrada son operaciones 'opuestas', cuadraremos ambos lados para eliminar el signo radical y resolver para la variable dentro.
Pero recuerda que cuando escribimos\(\sqrt{a}\) nos referimos a la raíz cuadrada principal. Así que\(\sqrt{a} \ge 0\) siempre. Cuando resolvemos ecuaciones radicales al cuadrar ambos lados podemos obtener una solución algebraica que haría\(\sqrt{a}\) negativa. Esta solución algebraica no sería una solución a la ecuación radical original; es una solución ajena. También vimos soluciones extrañas cuando resolvimos ecuaciones racionales.
Para la ecuación\(\sqrt{x+2}=x\):
- ¿Es x=2 una solución?
- ¿Es x=−1 una solución?
- Responder
-
1. ¿Es x=2 una solución?
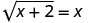
Dejar x = 2. 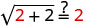
Simplificar. 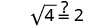
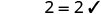
2 es una solución. 2. ¿Es x=−1 una solución?
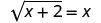
Dejar x = −1. 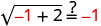
Simplificar. 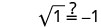
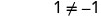
−1 no es una solución. −1 es una solución extraña a la ecuación.
Para la ecuación\(\sqrt{x+6}=x\):
- ¿Es x=−2 una solución?
- ¿Es x=3 una solución?
- Responder
-
- no
- si
Para la ecuación\(\sqrt{−x+2}=x\):
- ¿Es x=−2 una solución?
- ¿Es x=1 una solución?
- Responder
-
- no
- si
Para\(a \ge 0\),\((\sqrt{a})^2=a\)
Cómo Resolver Ecuaciones Radales
Resolver:\(\sqrt{2x−1}=7\)
- Responder
-
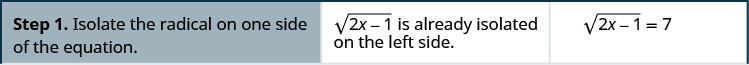



Resolver:\(\sqrt{3x−5}=5\).
- Responder
-
10
Resolver:\(\sqrt{4x+8}=6\).
- Responder
-
7
- Aísle el radical en un lado de la ecuación.
- Cuadrar ambos lados de la ecuación.
- Resuelve la nueva ecuación.
- Consulta la respuesta.
Resolver:\(\sqrt{5n−4}−9=0\).
- Responder
-
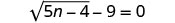
Para aislar el radical, agregue 9 a ambos lados. 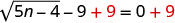
Simplificar. 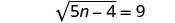
Cuadrar ambos lados de la ecuación. 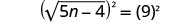
Resuelve la nueva ecuación. 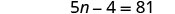


Consulta la respuesta.

La solución es n = 17.
Resolver:\(\sqrt{3m+2}−5=0\).
- Responder
-
\(\frac{23}{3}\)
Resolver:\(\sqrt{10z+1}−2=0\).
- Responder
-
\(\frac{3}{10}\)
Resolver:\(\sqrt{3y+5}+2=5\).
- Responder
-
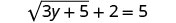
Para aislar el radical, restar 2 de ambos lados. 
Simplificar. 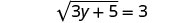
Cuadrar ambos lados de la ecuación. 
Resuelve la nueva ecuación. 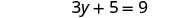

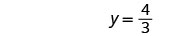
Consulta la respuesta.
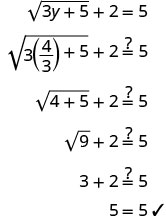
La solución es\(y=\frac{4}{3}\)
Resolver:\(\sqrt{3p+3}+3=5\).
- Responder
-
\(\frac{1}{3}\)
Resolver:\(\sqrt{5q+1}+4=6\).
- Responder
-
\(\frac{3}{5}\)
Cuando usamos un signo radical, nos referimos a la raíz principal o positiva. Si una ecuación tiene una raíz cuadrada igual a un número negativo, esa ecuación no tendrá solución.
Resolver:\(\sqrt{9k−2}+1=0\).
- Responder
-
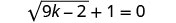
Para aislar el radical, restar 1 de ambos lados. 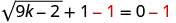
Simplificar. 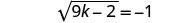
Dado que la raíz cuadrada es igual a un número negativo, la ecuación no tiene solución.
Resolver:\(\sqrt{2r−3}+5=0\)
- Responder
-
no hay solución
Resolver:\(\sqrt{7s−3}+2=0\).
- Responder
-
no hay solución
\[\begin{array}{cc} {(a+b)^2=a^2+2ab+b^2}&{(a−b)^2=a^2−2ab+b^2}\\ \nonumber \end{array}\]
¡No olvides el término medio!
Resolver:\(\sqrt{p−1}+1=p\).
- Responder
-
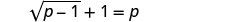
Para aislar el radical, restar 1 de ambos lados. 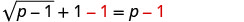
Simplificar. 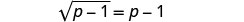
Cuadrar ambos lados de la ecuación. 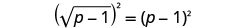
Simplifica, luego resuelve la nueva ecuación. 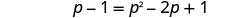
Es una ecuación cuadrática, así que consigue cero en un lado. 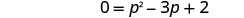
Factorar el lado derecho. 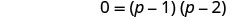
Utilice la propiedad cero del producto. 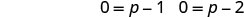
Resuelve cada ecuación. 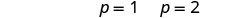
Consulta las respuestas.
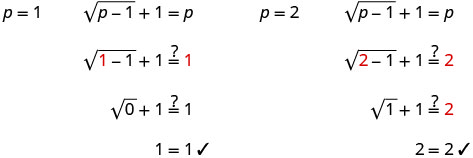
Las soluciones son p = 1, p = 2.
Resolver:\(\sqrt{x−2}+2=x\).
- Responder
-
2, 3
Resolver:\(\sqrt{y−5}+5=y\).
- Responder
-
5, 6
Resolver:\(\sqrt{r+4}−r+2=0\).
- Responder
-
\(\sqrt{r+4}−r+2=0\) Aislar el radical. \(\sqrt{r+4}=r−2\) Cuadrar ambos lados de la ecuación. \((\sqrt{r+4})^2=(r−2)^2\) Resuelve la nueva ecuación. \(r+4=r^2−4r+4\) Es una ecuación cuadrática, así que consigue cero en un lado. \(0=r^2−5r\) Factorar el lado derecho. \(0=r(r−5)\) Utilice la propiedad cero del producto. 0=r 0=r−5 Resuelve la ecuación. r=0 r=5 Consulta la respuesta.
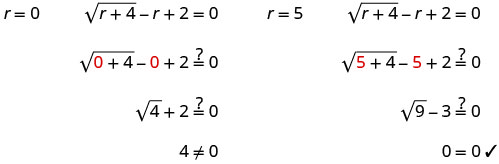
r=5 r=0 es una solución ajena.
Resolver:\(\sqrt{m+9}−m+3=0\).
- Responder
-
7
Resolver:\(\sqrt{n+1}−n+1=0\)
- Responder
-
3
Cuando hay un coeficiente frente al radical, debemos cuadrarlo, también.
Resolver:\(3\sqrt{3x−5}−8=4\).
- Responder
-
\(3\sqrt{3x−5}−8=4\) Aislar el radical. \(3\sqrt{3x−5}=12\) Cuadrar ambos lados de la ecuación. \((3\sqrt{3x−5})^2=(12)^2\) Simplifica, luego resuelve la nueva ecuación. 9 (3x−5) =144 Distribuir. 27x−45=144 Resuelve la ecuación. 27x=189 x=7 Consulta la respuesta.
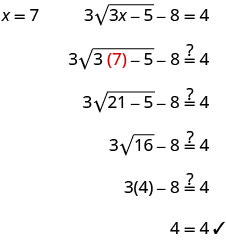
La solución es x=7.
Resolver:\(\sqrt{24a+2}−16=16\).
- Responder
-
\(\frac{127}{2}\)
Resolver:\(\sqrt{36b+3}−25=50\).
- Responder
-
\(\frac{311}{3}\)
Resolver:\(\sqrt{4z−3}=\sqrt{3z+2}\).
- Responder
-
\(\sqrt{4z−3}=\sqrt{3z+2}\) Los términos radicales están aislados \(\sqrt{4z−3}=\sqrt{3z+2}\) Cuadrar ambos lados de la ecuación. \((\sqrt{4z−3})^2=(\sqrt{3z+2})^2\) Simplifica y luego resuelve la nueva ecuación 4z−3=3z+2 z−3=2 z=5 x=7 Consulta la respuesta.
¡Te dejamos que demuestres que 5 cheques!
La solución es z=5.
Resolver:\(\sqrt{2x−5}=\sqrt{5x+3}\).
- Responder
-
no hay solución
Resolver:\(\sqrt{7y+1}=\sqrt{2y−5}\).
- Responder
-
no hay solución
A veces después de cuadrar ambos lados de una ecuación, todavía tenemos una variable dentro de un radical. Cuando eso sucede, repetimos el Paso 1 y el Paso 2 de nuestro procedimiento. Aislamos de nuevo el radical y el cuadrado a ambos lados de la ecuación.
Resolver:\(\sqrt{m}+1=\sqrt{m+9}\).
- Responder
-
\(\sqrt{m}+1=\sqrt{m+9}\) El radical del lado derecho está aislado.
Cuadrado ambos lados
\((\sqrt{m}+1)^2=(\sqrt{m+9})^2\) Simplifica: ¡ten mucho cuidado a medida que te multiplicas! \(m+2\sqrt{m}+1=m+9\) Todavía hay un radical en la ecuación.
Por lo que debemos repetir los pasos anteriores. Aislar el radical.
\(2\sqrt{m}=8\) Cuadrado a ambos lados. \((2\sqrt{m})^2=(8)^2\) Simplifica, luego resuelve la nueva ecuación. 4m=64 m=16 Consulta la respuesta.
Te dejamos a ti demostrar que m=16 cheques!
La solución es m=16.
Resolver:\(\sqrt{x}+3=\sqrt{x+5}\).
- Responder
-
no hay solución
Resolver:\(\sqrt{m}+5=\sqrt{m+16}\).
- Responder
-
no hay solución
Resolver:\(\sqrt{q−2}+3=\sqrt{4q+1}\).
- Responder
-
\(\sqrt{q−2}+3=\sqrt{4q+1}\) El radical del lado derecho está aislado.
Cuadrado ambos lados
\((\sqrt{q−2}+3)^2=(\sqrt{4q+1})^2\) Simplificar. \(q−2+6\sqrt{q−2}+9=4q+1\) Todavía hay un radical en la ecuación.
Por lo que debemos repetir los pasos anteriores. Aislar el radical.
\(6\sqrt{q−2}=3q−6\) Cuadrado a ambos lados. \((6\sqrt{q−2})^2=(3q−6)^2\) Simplifica, luego resuelve la nueva ecuación. \(36(q−2)=9q^2−36q+36\) Distribuir. \(36q−72=9q^2−36q+36\) Es una ecuación cuadrática, así que consigue cero en un lado. \(0=9q^2−72q+108\) Factorar el lado derecho. \(0=9(q^2−8q+12)\)
\(0=9(q−6)(q−2)\)
Usar la propiedad cero del producto \[\begin{array}{ll} {q−6=0}&{q−2=0}\\ {q=6}&{q=2}\\ \nonumber \end{array}\] Los cheques te quedan a ti. (Ambas soluciones deberían funcionar.)
Las soluciones son q=6 y q=2.
Resolver:\(\sqrt{y−3}+2=\sqrt{4y+2}\).
- Responder
-
no hay solución
Resolver:\(\sqrt{n−4}+5=\sqrt{3n+3}\).
- Responder
-
no hay solución
Uso de Raíces Cuadradas en Aplicaciones
A medida que avanzas en tus cursos universitarios, encontrarás fórmulas que incluyen raíces cuadradas en muchas disciplinas. Ya hemos utilizado fórmulas para resolver aplicaciones de geometría.
Utilizaremos nuestra Estrategia de Resolución de Problemas para Aplicaciones Geométricas, con ligeras modificaciones, para darnos un plan de resolución de aplicaciones con fórmulas de cualquier disciplina.
- Lee el problema y asegúrate de que se entiendan todas las palabras e ideas. Cuando corresponda, dibuje una figura y etiquétela con la información dada.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando eligiendo una variable para representarlo.
- Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
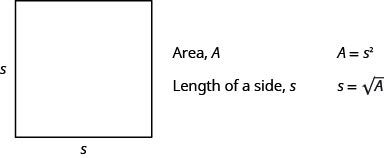
Se utilizó la fórmula A=L·W para encontrar el área de un rectángulo con largo L y ancho W. Un cuadrado es un rectángulo en el que la longitud y la anchura son iguales. Si dejamos s ser la longitud de un lado de un cuadrado, el área del cuadrado es\(s^2\).
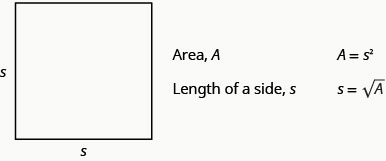
La fórmula nos\(A=s^2\) da el área de un cuadrado si conocemos la longitud de un lado. ¿Y si queremos encontrar la longitud de un lado para un área determinada? Entonces necesitamos resolver la ecuación para s.
\[\begin{array}{ll} {}&{A=s^2}\\ {\text{Take the square root of both sides.}}&{\sqrt{A}=\sqrt{s^2}}\\ {\text{Simplify.}}&{s=\sqrt{A}}\\ \nonumber \end{array}\]
Podemos usar la fórmula\(s=\sqrt{A}\) para encontrar la longitud de un lado de un cuadrado para un área determinada.
Mostraremos un ejemplo de esto en el siguiente ejemplo.
Mike y Lychelle quieren hacer un patio cuadrado. Tienen suficiente concreto para pavimentar un área de 200 pies cuadrados. Usa la fórmula\(s=\sqrt{A}\) para encontrar la longitud de cada lado del patio. Redondee su respuesta a la décima de pie más cercana.
- Responder
-
Paso 1. Lee el problema. Dibuja una figura y
etiquétalo con la información dada.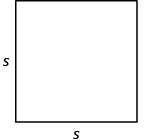
A = 200 pies cuadrados Paso 2. Identifica lo que buscas. La longitud de un lado del patio cuadrado. Paso 3. Nombra lo que buscas
eligiendo una variable para representarlo.Vamos s = la longitud de un lado. Paso 4. Traduzca en una ecuación escribiendo la fórmula o modelo
apropiado para la situación.
Sustituir la información dada.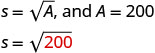
Paso 5. Resolver la ecuación usando buenas
técnicas de álgebra. Redondear a una posición decimal.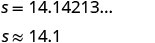
Paso 6. Comprueba la respuesta en el problema y
asegúrate de que tenga sentido.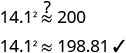
Esto está lo suficientemente cerca porque redondeamos la raíz
cuadrada.
¿Es razonable un patio con 14.1 pies laterales?
Sí.Paso 7. Contesta la pregunta con una
oración completa.Cada lado del patio debe ser de 14.1 pies.
Katie quiere plantar un césped cuadrado en su patio delantero. Tiene suficiente césped para cubrir un área de 370 pies cuadrados. Usa la fórmula\(s=\sqrt{A}\) para encontrar la longitud de cada lado de su césped. Redondee su respuesta a la décima de pie más cercana.
- Responder
-
19.2 pies
Sergio quiere hacer un mosaico cuadrado como incrustación para una mesa que está construyendo. Tiene loseta suficiente para cubrir un área de 2704 centímetros cuadrados. Usa la fórmula\(s=\sqrt{A}\) para encontrar la longitud de cada lado de su mosaico. Redondee su respuesta a la décima de pie más cercana.
- Responder
-
52.0 cm
Otra aplicación de raíces cuadradas tiene que ver con la gravedad.
En la Tierra, si se deja caer un objeto desde una altura de hh pies, el tiempo en segundos que tardará en llegar al suelo se encuentra usando la fórmula,
\(t=\frac{\sqrt{h}}{4}\)
Por ejemplo, si un objeto se deja caer desde una altura de 64 pies, podemos encontrar el tiempo que lleva llegar al suelo sustituyendo h=64 en la fórmula.
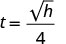 |
|
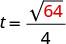 |
|
| Toma la raíz cuadrada de 64. | 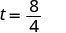 |
| Simplifica la fracción. | 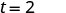 |
Tomaría 2 segundos para que un objeto caído desde una altura de 64 pies llegue al suelo.
Christy dejó caer sus gafas de sol desde un puente a 400 pies sobre un río. Usa la fórmula\(t=\frac{\sqrt{h}}{4}\) para encontrar cuántos segundos tardaron las gafas de sol en llegar al río.
- Responder
-
Paso 1. Lee el problema. Paso 2. Identifica lo que buscas. El tiempo que tardan las gafas de sol en llegar
al río.Paso 3. Nombra lo que buscas
eligiendo una variable para representarlo.Dejar t = tiempo. Paso 4. Traduzca en una ecuación escribiendo la fórmula o modelo
apropiado para la situación.
Sustituir en la información dada.

Paso 5. Resolver la ecuación usando buenas
técnicas de álgebra.

Paso 6. Comprueba la respuesta en el problema y
asegúrate de que tenga sentido.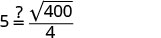

5=5 ✓¿5 segundos parecen razonables?
Sí.Paso 7. Contesta la pregunta con una
oración completa.Tardarán 5 segundos para que las gafas de sol choquen con
el agua.
Un helicóptero arrojó un paquete de rescate desde una altura de 1,296 pies. Usa la fórmula\(t=\frac{\sqrt{h}}{4}\) para encontrar cuántos segundos tardó el paquete en llegar al suelo.
- Responder
-
9 segundos
Un lavaparabrisas dejó caer una escobilla de goma desde una plataforma\(t=\frac{\sqrt{h}}{4}\) a 196 pies sobre la acera Usa la fórmula para encontrar cuántos segundos tardó en llegar a la acera.
- Responder
-
3.5 segundos
Los policías que investigan accidentes automovilísticos miden la longitud de las marcas de derrape en el pavimento. Entonces usan raíces cuadradas para determinar la velocidad, en millas por hora, un automóvil iba antes de aplicar los frenos.
Si la longitud de las marcas de derrape es d pies, entonces la velocidad, s, del automóvil antes de que se aplicaran los frenos se puede encontrar usando la fórmula,
\(s=\sqrt{24d}\)
Después de un accidente automovilístico, las marcas de derrape de un auto medían 190 pies. Usa la fórmula\(s=\sqrt{24d}\) para encontrar la velocidad del auto antes de que se aplicaran los frenos. Redondee su respuesta a la décima más cercana.
- Responder
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. La velocidad de un auto. Paso 3. Nombra lo que estamos buscando. Vamos s = la velocidad. Paso 4. Traduzca en una ecuación escribiendo la fórmula apropiada. 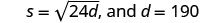
Sustituir la información dada. 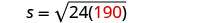
Paso 5. Resuelve la ecuación. 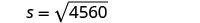
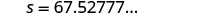
Redondear a 1 decimal. 
Paso 6. Consulta la respuesta en el problema.
67.5≈? 24 (190)
67.5≈?
456067.5≈? 67.5277...¿Es 67.5 mph una velocidad razonable? Sí. Paso 7. Contesta la pregunta con una oración completa. La velocidad del auto era de aproximadamente 67.5 millas por hora.
Un investigador de accidentes midió las marcas de derrape del automóvil. La longitud de las marcas de derrape era de 76 pies. Usa la fórmula\(s=\sqrt{24d}\) para encontrar la velocidad del auto antes de que se aplicaran los frenos. Redondee su respuesta a la décima más cercana.
- Responder
-
42.7 pies
Las marcas de derrape de un vehículo involucrado en un accidente fueron de 122 pies de largo. Usa la fórmula\(s=\sqrt{24d}\) para encontrar la velocidad del vehículo antes de que se aplicaran los frenos. Redondee su respuesta a la décima más cercana.
- Responder
-
54.1 pies
Conceptos clave
- Para resolver una ecuación radical:
- Aísle el radical en un lado de la ecuación.
- Cuadrar ambos lados de la ecuación.
- Resuelve la nueva ecuación.
- Consulta la respuesta. Algunas soluciones obtenidas pueden no funcionar en la ecuación original.
- Resolver aplicaciones con fórmulas
- Lee el problema y asegúrate de que se entiendan todas las palabras e ideas. Cuando corresponda, dibuje una figura y etiquétela con la información dada.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando eligiendo una variable para representarlo.
- Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
- Área de un cuadrado
- Objetos que caen
- En la Tierra, si se deja caer un objeto desde una altura de hh pies, el tiempo en segundos que tardará en llegar al suelo se encuentra usando la fórmula\(t=\frac{\sqrt{h}}{4}\).
- Marcas de derrape y velocidad de un automóvil
- Si la longitud de las marcas de derrape es d pies, entonces la velocidad, s, del automóvil antes de que se aplicaran los frenos se puede encontrar usando la fórmula\(s=\sqrt{24d}\).
Glosario
- ecuación radical
- Una ecuación en la que la variable está en el radicando de una raíz cuadrada se denomina ecuación radical


