1.2: Factoraje
- Page ID
- 112009
En esta sección se revisarán tres de los tipos más comunes de factorización: factorizar un Factor Común Mayor, Factorización Trinomial y factorización de una Diferencia de Cuadrados.
Mayor factor común
La factorización de un factor común más grande deshace esencialmente la multiplicación distributiva que a menudo ocurre en las expresiones matemáticas. Este factor puede ser monomial o polinomio, pero en estos ejemplos, exploraremos factores comunes monomiales.
Al multiplicar\(3 x y^{2}(5 x-2 y)=15 x^{2} y^{2}-6 x y^{3}\) el término monomio\(3 x y^{2}\) se multiplica o distribuye a ambos términos dentro de los paréntesis. El proceso de factorización deshace esta multiplicación.
Ejemplo\(\PageIndex{1}\)
Factor
\[7 x^{2}+14 x \nonumber\]
Solución
Esta expresión tiene dos términos. Los coeficientes comparten un factor común de 7 y la única variable involucrada en esta expresión es\(x\). El mayor poder de la variable que es compartido por ambos términos es por\(x^{1},\) lo que este es el poder de\(x\) que se puede factorizar a partir de ambos términos. El mayor factor común es\(7 x\)
\[7 x^{2}+14 x=7 x(x+2) \nonumber\]
No es necesario encontrar el mayor factor común de inmediato. En problemas más complicados, la factorización se puede lograr en piezas, de manera similar a la reducción de fracciones.
Ejemplo\(\PageIndex{2}\)
Factor
\[42 x^{2} y^{6}+98 x y^{3}-210 x^{3} y^{2} \nonumber\]
Solución
Esta expresión tiene tres términos. No queda claro de inmediato cuál es el mayor factor común de los coeficientes, pero todos son números pares, así que al menos podríamos dividirlos a todos por\(2 .\) El\(98 x y^{3}\) término tiene un\(x^{1},\) lo que significa que este es el poder más alto del\(x\) que podríamos factorizar de todos los términos. El\(210 x^{3} y^{2}\) tiene un\(y^{2},\) que es el poder más alto de\(y\) que se puede factorizar de todos los términos. Así que al menos podemos proceder con estos factores:
\ [\ begin {alineado}
42 x^ {2} y^ {6} +98 x y^ {3} -210 x^ {3} y^ {2} &=2 x y^ {2} * 21 x y^ {4} +2 x y^ {2} * 49 y-2 x y^ {2} * 105 x^ {2}\
&=2 x y^ {2}\ izquierda (21 x y^ {4} +49 y-105 x^ {2}\ derecha)
\ final {alineado}\]
Ahora bien, no nos esforzamos mucho por encontrar el mayor factor común al inicio de este problema, por lo que es importante que sigamos cuestionándonos si quedan o no factores comunes restantes. Los 21 y 49 comparten claramente un factor común de\(7,\) por lo que tendría sentido ver si\(7\) también\(105\) es divisible por. Si dividimos\(105\) por\(7,\) vemos que\(105=7^{*} 15 .\) Así, también podemos factorizar un factor común de\(7\) a partir de los términos restantes entre paréntesis.
\ [\ comenzar {alineado}
2 x y^ {2}\ izquierda (21 x y^ {4} +49 y-105 x^ {2}\ derecha) &=2 x y^ {2}\ izquierda (7 * 3 x y^ {4} +7 * 7 y-7 * 15 x^ {2}\ derecha)\\
&=7 * 2 x y^ {2}\ izquierda (3 x y^ {4} +7 y-15 x^ {2}\ derecha)\\
&=14 x y^ {2}\ izquierda (3 x y^ {4} +7 y-15 x^ {2}\ derecha)
\ final {alineado }\]
Factoring Trinomial\((a=1)\)
El factoraje trinomial deshace la multiplicación de dos binomios, y viene en dos sabores: simple y complejo. La forma más simple de factorización trinomial implica una expresión trinomial en la forma\(a x^{2}+b x+c\) en que el valor de\(a\) es 1 Esto hace que la tarea de factorización sea más simple que si el valor de no\(a\) es 1.
Ejemplo\(\PageIndex{3}\)
\(x^{2}+7 x+10\)
Solución Factorial
En este ejemplo, el valor de\(a\) es el\(1,\) que hace que este tipo de factorización trinomial sea un poco menos difícil de lo que sería de otra manera. Sea o no el valor de\(a\) 1 la cuestión fundamental que rige este tipo de factorización es el\(+\) o\(-\) signo del término constante. En este problema, el término constante es positivo. Eso significa que necesitamos encontrar factores de 10 que se suman a\(7 .\) Esto es relativamente sencillo:
\[ x^{2}+7 x+10=(x+2)(x+5) \nonumber \]
Un problema acompañante para este es\(x^{2}-7 x+10\). Observe que, en este caso, el signo del término constante sigue siendo positivo, lo que significa que todavía necesitamos factores de 10 que sumen a\(7 .\) Esto significa que todavía necesitamos usar 2 y\(5 .\) Sin embargo, en este caso, en lugar de que el +10 se produzca a partir de una multiplicación de (+2) (+5) es el resultado de multiplicando\((-2)(-5) .\) Esto es lo que hace que el 7 en el segundo ejemplo sea negativo:
\[x^{2}-7 x+10=(x-2)(x-5) \nonumber\]
Ejemplo\(\PageIndex{4}\)
Factor\(x^{2}+3 x-10\)
Solución
En este caso, el signo del término constante es negativo. Eso quiere decir que necesitamos encontrar factores de 10 que tengan una diferencia de\(3 .\) Esto sigue siendo 5 y 2.
\[x^{2}+3 x-10=(x-2)(x+5) \nonumber\]
La multiplicación del (-2) y el (+5) producen el (-10) y el hecho de que el 2 y el 5 tengan signos opuestos crea la diferencia que nos da\((+3) .\) Un problema compañero a éste es\(x^{2}-3 x-10\). En este caso, el signo del término constante sigue siendo negativo, lo que significa que todavía necesitamos factores de 10 que tengan una diferencia de\(3 .\) Esto significa que todavía necesitamos usar 2 y\(5 .\) Sin embargo en este caso, en lugar del (+3) como coeficiente del término medio, necesitaremos un (-3). Para ello simplemente invertimos los signos del 2 y 5 del problema anterior:
\[x^{2}-3 x-10=(x+2)(x-5) \nonumber\]
Ahora el (+2) (-5) nos da\((-10),\) pero el nos\(+2 x-5 x\) da\((-3 x)\) en vez de\((+3 x)\).
Ejemplo\(\PageIndex{5}\)
Factor\(x^{2}+11 x-42\)
Solución
En este problema, el signo del término constante es negativo. Eso quiere decir que necesitamos factores de 42 que tengan una diferencia de\(11 .\) Una exploración sistemática de todos los pares de factores de 42 puede ayudarnos a encontrar el par correcto:
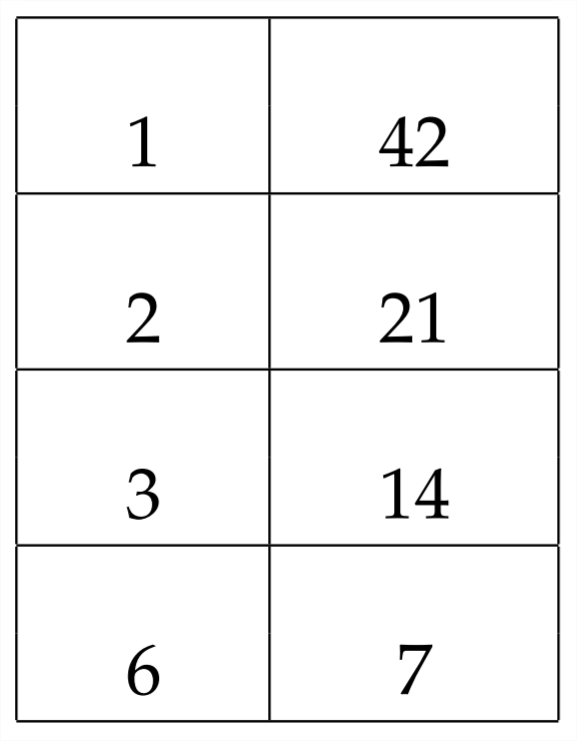
Aquí, podemos ver que los factores 3 y 14 tienen una diferencia de\(11 .\) Esto significa que usaremos estos factores en nuestra respuesta:\((x \quad 3)(x\)
14). Al determinar cómo colocar los\(-\) signos\(+\) y entre paréntesis, podemos referirnos al problema original:\(x^{2}+11 x-42 .\) Si queremos una diferencia de\((+11 x),\) entonces necesitaremos tener\(a(+14)\) y\(a(-3)\)
\[x^{2}+11 x-42=(x-3)(x+14) \nonumber\]
Ejemplo\(\PageIndex{6}\)
Factor\(x^{2}+28 x+96\)
Solución
En este problema, el signo del término constante es positivo. Eso significa que necesitamos factores de 96 que se sumen a\(28 .\) Una exploración sistemática de todos los pares de factores de 96 nos puede ayudar a encontrar el par correcto:
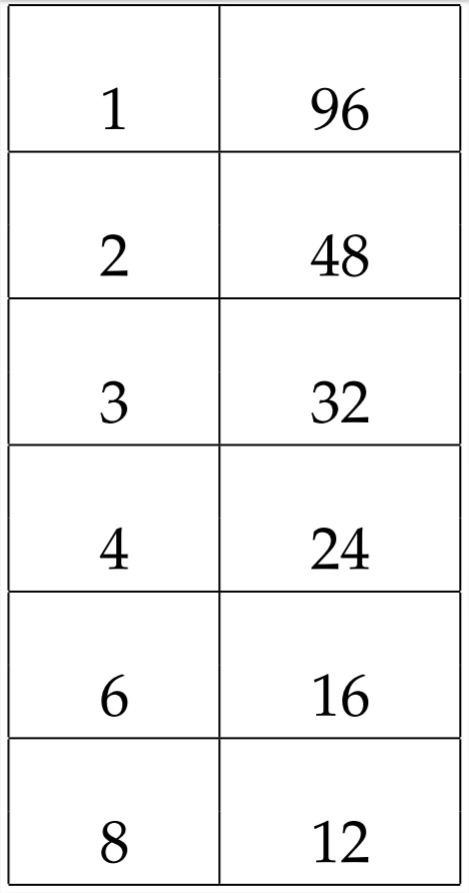
Aquí, podemos ver que los factores 4 y 24 suman a\(28 .\) Esto significa que usaremos estos factores en nuestro respuesta:\((x \quad 4)(x \quad 24) .\) Al determinar cómo colocar los\(-\) signos\(+\) y entre paréntesis, podemos referirnos al problema original:
\(x^{2}+28 x+96 .\)Si queremos que 4 y 24 sumen\((+28),\) entonces ambos deberían ser positivos:
\[x^{2}+28 x+96=(x+4)(x+24) \nonumber\]
Al construir los gráficos de pares de factores en los dos problemas anteriores, nada más difícil que dividir el término constante por los números\(1,2,3,4,5,6, \dots\) y así sucesivamente puede ayudarte a encontrar la lista completa de pares de factores. Si no obtiene un número entero al dividir, por ejemplo,\(96 \div 5=19.2,\) entonces este número no se incluye en la lista de pares de factores.
Factoring Trinomial\((a \neq 1)\)
Si el valor de no\(a\) es\(1,\) esto significa que, si el trinomio es factorizable, al menos uno de sus factores binomiales también tiene un coeficiente distinto a\(1 .\) Por ejemplo:
\[(2 x+7)(x-3)=2 x^{2}+1 x-21 \nonumber\]
Si intentáramos deshacer esta multiplicación a través del proceso de factorización trinomial, deberíamos mirar hacia el signo del término constante. En este ejemplo, el signo es negativo. Esto todavía significa que necesitaremos encontrar pares de factores que produzcan una diferencia de\((+1 x)\) como el término medio. Sin embargo, en este escenario, no son solo los factores de 21 los que intervienen en producir el\((+1 x),\) sino la combinación de los factores de 21 y los factores del coeficiente principal\(2 .\) El término medio\((+1 x)\) proviene de la multiplicación de la\((2 x)(-3)\) y la multiplicación de (+7) \((+1 x)\)
\ [
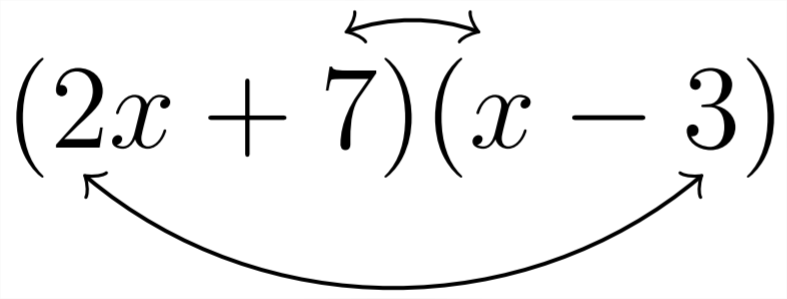
\ begin {alineado}
(2 x+7) (x-3) &=2 x^ {2} -6 x+7 x-21\\
&=2 x^ {2} +x-21
\ end {alineado}
\]
Al tratar de factorizar un trinomio como\(2 x^{2}+x-21\), necesitamos tomar esto en consideración. Por ejemplo, si tuviéramos que factorizar\(3 x^{2}-10 x+8\), primero debemos seguir mirando el signo del término constante, que, en este caso, es positivo. Eso significa que queremos pares de factores que se sumen a\(10 .\) Pero tenemos que tomar en consideración la interacción de los factores del 3 con los factores del\(8 .\) El 3 es un número primo, lo que significa que no tenemos opción, solo se puede dividir en\(3 * 1,\) para que podamos comenzar:
\[\text { Factor } 3 x^{2}+10 x+8\]
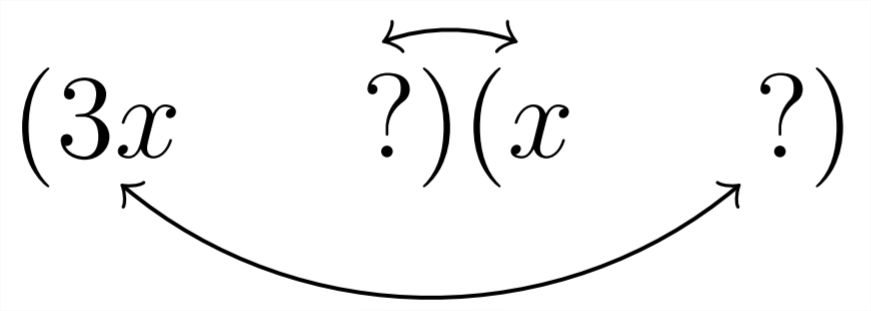
Nuestras opciones para rellenar los signos de interrogación vendrán de los factores de 8, ya sea\(8 * 1\) o\(4 * 2 .\) El proceso es por ensayo y error:
Podemos ver que la elección anterior:
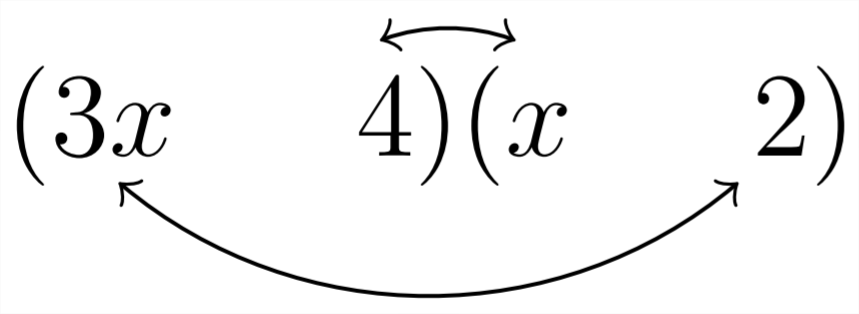
nos da\(10 x\) lo requerido como el término medio. ya que el problema original era\(3 x^{2}+10 x+8\) vamos a querer rellenar los signos como ambos positivos:
\[3 x^{2}+10 x+8=(3 x+4)(x+2)\]
Un segundo método para manejar este tipo de factorización depende de cómo los factores del coeficiente principal y el término constante interactúan entre sí para producir el término medio. En este proceso, dado el problema\(3 x^{2}+10+8\), podemos multiplicar el primer y último coeficiente y luego mirar los pares de factores del producto:
\[3 * 8=24\]
| 1 | 24 |
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
Podemos ver que el par de factores de 24 que suma 10 es\(6 * 4 .\) Procedemos dividiendo el\(10 x\) en\(6 x+4 x\) y luego factor por agrupación. Si te incomoda factorizar agrupando, entonces este probablemente no sea un buen método para probar. Sin embargo, si se siente cómodo con la factorización por agrupación, el resto del proceso es relativamente sencillo:
\[3 x^{2}+10 x+8=3 x^{2}+6 x+4 x+8\]
Luego factorizamos un factor común de los dos primeros términos y los dos últimos términos por separado, y luego factorizamos el factor binomial común de\((x+2)\)
\ [\ begin {alineado}
3 x^ {2} +10 x+8 &=3 x^ {2} +6 x+4 x+8\\
&=3 x (x+2) +4 (x+2)\\
& =( x+2) (3 x+4)
\ end {alineado}\]
Ejemplo\(\PageIndex{7}\)
Factor\(7 x^{2}-5 x-18\)
Solución
En este ejemplo, el signo del término constante es negativo, lo que significa que necesitaremos pares de factores que produzcan una diferencia de\(5 .\) El coeficiente principal es el\(7,\) que es primo, así que, nuevamente, la única forma de dividir el 7 es\(7 * 1\)
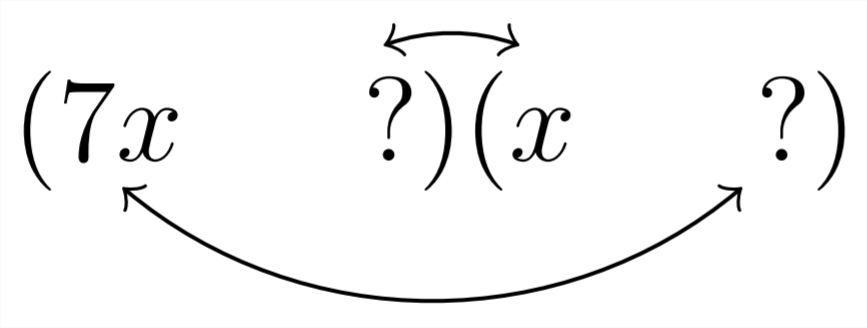
Las opciones para rellenar los signos de interrogación provienen de los factores\(18,\) para los que existen tres posibilidades:\(18 * 1,9 * 2,\) o\(6 * 3 .\) Intentaremos cada uno de estos pares de factores en lugar de los signos de interrogación:
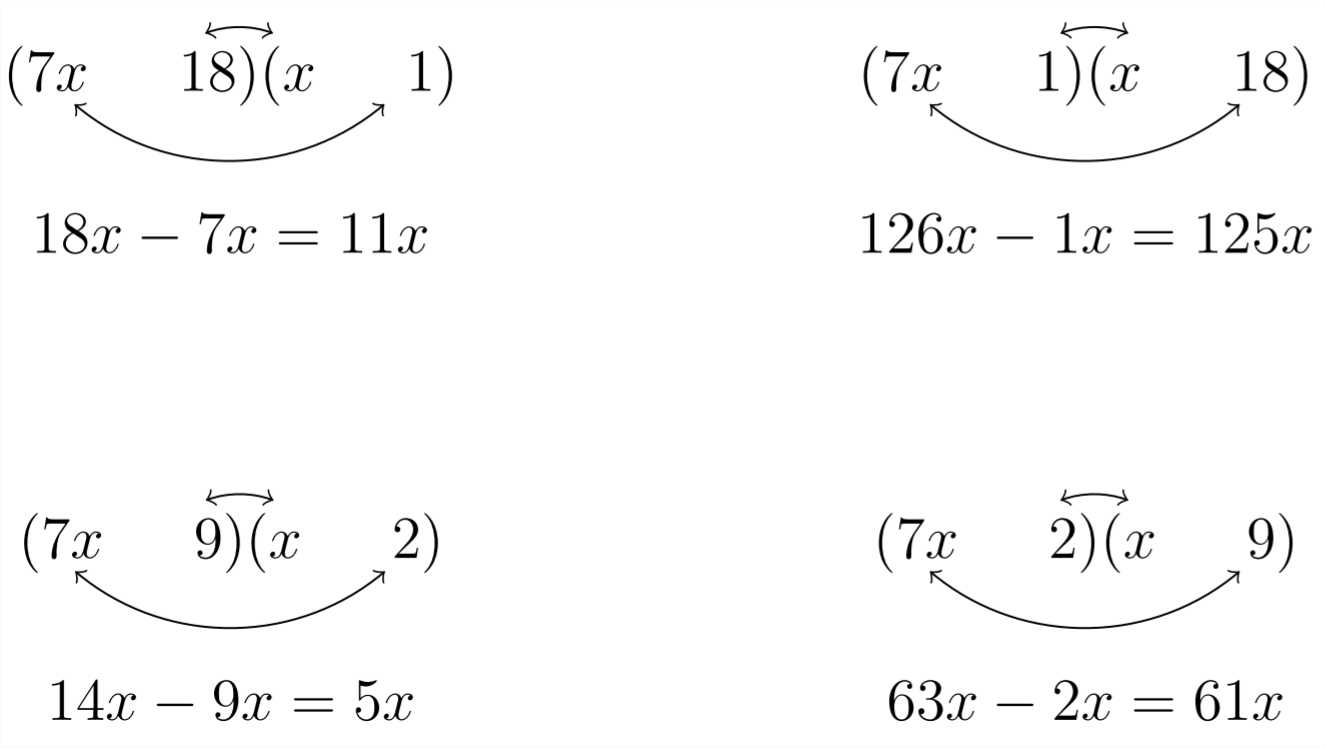
La elección anterior:
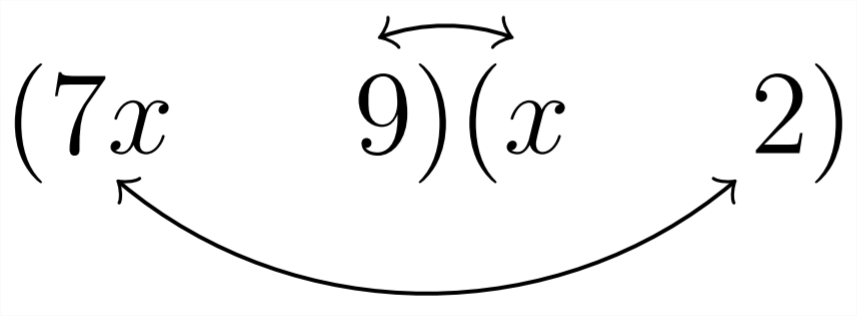
nos da\(5 x\) lo requerido como el término medio. ya que estamos buscando una\((-5 x),\) haremos los 14 negativos y los 9 positivos:\(-14 x+9 x=-5 x\)
\[7 x^{2}-5 x-18=(7 x+9)(x-2) \nonumber\]
Si queremos probar el otro método para factorizar\(7 x^{2}-5 x-18\), nos multiplicaríamos\(7 * 18=126,\) y luego trabajaríamos para encontrar pares de factores de 126 que tengan una diferencia de 5
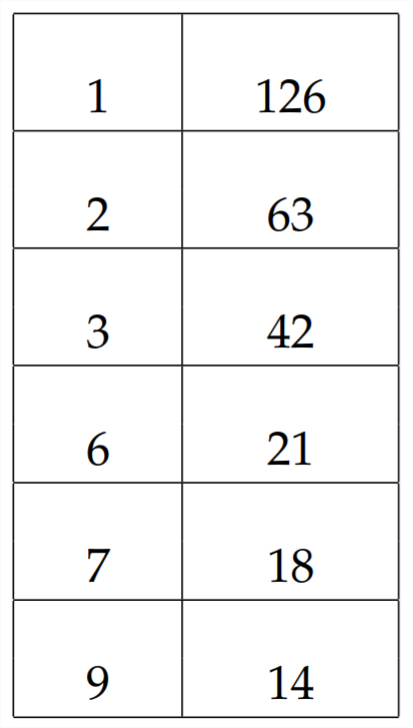
Aquí, el último par de factores\(9 * 14\),, tiene una diferencia de\(5 .\) Entonces entonces procedemos a factor agrupando:
\ [
\ begin {aligned}
7 x^ {2} -5 x-18 &=7 x^ {2} +9 x-14 x-18\\
&=x (7 x+9) -2 (7 x+9)\\
& =( 7 x+9) (x-2)
\ end {alineado}
\]
Observe que cuando el -2 fue factorizado de los dos últimos términos\(-14 x-18\), terminamos con\(-2(7 x+9)\), porque\((-2) *(+9)=-18 .\) Esto también es importante porque para factorizar el factor binomial común de\((7 x+9),\) este binomio debe ser exactamente el mismo en ambos términos.
Diferencia de Cuadrados
Factorizar una diferencia de cuadrados es en realidad una forma especial de factorización trinomial. Si consideramos un trinomio de la forma\(a x^{2}+b x+c,\) donde\(c\) es un cuadrado perfecto y negativo, encontraremos algo interesante sobre los posibles valores de\(b\) que hacen factorizable al trinomio.
Ejemplo
\ [
\ text {Considera} x^ {2} +b x-36
\]
Para que esta expresión sea factorizable, el coeficiente medio\(b\) tendría que ser igual a la diferencia de cualquiera de los pares de factores de\(36 .\) Si miramos el factor posible pares, vemos lo siguiente:
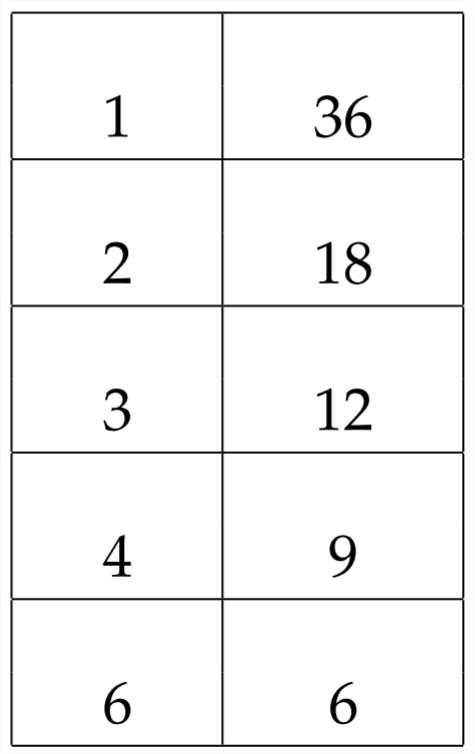
Esto significa que los valores posibles para\(b\) eso harían factorizable esta expresión son:
\ [
\ begin {array} {c}
36-1=35\ rightarrow x^ {2} +35 x-36 =( x+36) (x-1)\\
18-2=16\ rightarrow x^ {2} +16 x-36 =( x+18) (x-2)\\
12-3=9\ rightarrow x^ {2} +9 x-36= (x+12) (x-3)\
9-4=5\ fila derecha x^ {2} +5 x-36 =( x+9) (x-4)\
6-6=0\ fila derecha x^ {2} +0 x-36=x^ {2} -36 =( x+6) (x-6)
\ end {array}
\]
Como vemos, factorizar\(x^{2}-36\) significa que los factores de la plaza perfecta\(36=6 * 6\) se cancelarán entre sí dejando\(0 x\) en el medio. Si hay un cuadrado perfecto como coeficiente inicial, entonces este número también debe tener raíces cuadradas:
\ [
16 x^ {2} -25 =( 4 x+5) (4 x-5)
\]
En el ejemplo anterior, el\(+20 x\) y\(-20 x\) como los términos medios se cancelan entre sí dejando solo \(16 x^{2}-25\)
Estos tres tipos de factoring también se pueden combinar entre sí como vemos en los siguientes ejemplos.
Ejemplo\(\PageIndex{6}\)
Factor\(2 x^{2}-50\)
Solución
Esto no es un trinomio porque no tiene tres términos. Tampoco es una diferencia de cuadrados porque 2 y 50 no son cuadrados perfectos. Sin embargo, hay un factor común de 2 que podemos factorizar:
\ [
2 x^ {2} -50=2\ left (x^ {2} -25\ right)
\]
La expresión dentro de los paréntesis es una diferencia de cuadrados y debe ser factorizada:
\ [
2 x^ {2} -50=2\ left (x^ {2} -25\ derecha) =2 (x+5) (x-5)
\]
Ejemplo\(\PageIndex{7}\)
Factor\(24-2 x-x^{2}\)
Solución
Aquí el signo del\(x^{2}\) término es negativo. Para este problema podemos factorizar\(a-1\) y proceder como hicimos con los problemas anteriores en los que el coeficiente principal era positivo o podemos factorizarlo como es:
\ [
24-2 x-x^ {2} =-\ left (x^ {2} +2 x-24\ right) =- (x+6) (x-4)
\]
Si queremos factorizarlo tal como es, debemos ser conscientes de que el término constante es positivo y el término cuadrático es negativo, lo que significa que vamos a querer que los factores de 24 tengan una diferencia de 2
\ [
24-2 x-x^ {2} =( 6+x) (4-x)
\]
Ejemplo\(\PageIndex{8}\)
Factor\(6 x^{2}+12 x+6\)
Solución
Primero, notamos que esta expresión tiene un factor común de\(6 .\) Si factorizamos el
\(6,\) entonces deberíamos quedarnos con un problema más fácil:
\ [
6 x^ {2} +12 x+6=6\ left (x^ {2} +2 x+1\ right) =6 (x+1) (x+1) =6 (x+1) =6 (x+1) ^ {2}
\]
Ejercicios\(\PageIndex{1}\)
Factorizar cada expresión completamente.
1)\(\quad 8 a^{2} b^{3}+24 a^{2} b^{2}\)
2)\(\quad 19 x^{2} y-38 x^{2} y^{3}\)
3)\(\quad 13 t^{8}+26 t^{4}-39 t^{2}\)
4)\(\quad 5 y^{5}+25 y^{4}-20 y^{3}\)
5)\(\quad 45 m^{4} n^{5}+36 m n^{6}+81 m^{2} n^{3}\)
6)\(\quad125 x^{3} y^{5}+60 x^{4} y^{4}-85 x^{5} y^{2}\)
Factorizar cada trinomio en el producto de dos binomios.
7)\(\quad a^{2}+3 a+2\)
8)\(\quad y^{2}-8 y-48\)
9)\(\quad x^{2}-6 x-27\)
10)\(\quad t^{2}-13 t+42\)
11)\(\quad m^{2}+3 m-54\)
12)\(\quad x^{2}+11 x+24\)
Factorizar completamente. Recuerda buscar primero un factor común. Si el polinomio es primo, indíquelo.
13)\(\quad a^{2}-9\)
14)\(\quad y^{2}-121\)
15)\(\quad -49+k^{2}\)
16)\(\quad -64+t^{2}\)
17)\(\quad 6 x^{2}-54\)
18)\(\quad 25 y^{2}-4\)
19)\(\quad 200-2 a^{2}\)
20)\(\quad 3 m^{2}-12\)
21)\(\quad 98-8 k^{2}\)
22) \(\quad -80 w^{2}+45\)
23)\(\quad 5 y^{2}-80\)
24)\(\quad -4 a^{2}+64\)
25)\(\quad 8 y^{2}-98\)
26)\(\quad 24 a^{2}-54\)
27)\(\quad 36 k-49 k^{3}\)
28)\(\quad 16 y-81 y^{3}\)
Factorizar cada trinomio completamente. Recuerda buscar primero un factor común. Si el polinomio es primo, indíquelo.
29)\(\quad 3 y^{2}-15 y+16\)
30)\(\quad 8 a^{2}-14 a+3\)
31)\(\quad 9 x^{2}-18 x+8\)
32)\(\quad 6 a^{2}-17 a+12\)
33)\(\quad 2 x^{2}+7 x+6\)
34)\(\quad 2 m^{2}+13 m-18\)
35)\(\quad 20 y^{2}+22 y+6\)
36)\(\quad 36 x^{2}+81 x+45\)
37)\(\quad 24 a^{2}-42 a+9\)
38)\(\quad 48 x^{2}-74 x-10\)
Factorizar cada expresión completamente.
39)\(\quad 30+7 y-y^{2}\)
40)\(\quad 45+4 a-a^{2}\)
41)\(\quad 24-10 x-x^{2}\)
42)\(\quad 36-9 x-x^{2}\)
43)\(\quad 84-8 x-x^{2}\)
44)\(\quad 72-6 a-a^{2}\)
45)\(\quad 6 y^{2}+24 y+15\)
46)\(\quad 10 y^{2}-75 y+35\)
47)\(\quad 20 a x^{2}-36 a x-8 a\)
- Responder
-
1)\(\quad 8 a^{2} b^{2}(b+3)\)
3)\(\quad 13 t^{2}\left(t^{6}+2 t^{2}-3\right)\)
5)\(\quad 9 m n^{3}\left(5 m^{3} n^{2}+4 n^{3}+9 m\right)\)
7)\(\quad (a+2)(a+1)\)
9)\(\quad (x-9)(x+3)\)
11)\(\quad (m+9)(m-6)\)
13)\(\quad (a+3)(a-3)\)
15)\(\quad (k+7)(k-7)\)
17)\(\quad 6(x+3)(x-3)\)
19)\(\quad 2(10+a)(10-a)\)
21)\(\quad 2(7+2 k)(7-2 k)\)
23)\(\quad 5(y+4)(y-4)\)
25)\(\quad 2(2 y+7)(2 y-7)\)
27)\(\quad k(6+7 k)(6-7 k)\)
29)\(\quad\) PRIME
31)\(\quad(3 x-4)(3 x-2)\)
33)\(\quad(2 x+3)(x+2)\)
35) \(\quad 2(5 y+3)(2 y+1)\)
37)\(\quad 3(2 a-3)(4 a-1)\)
39)\(\quad(10-y)(3+y)\)
41)\(\quad(12+x)(2-x)\)
43)\(\quad(14+x)(6-x)\)
45)\(\quad 3\left(2 y^{2}+8 y+5\right)\)
47)\(\quad 4 a(5 x+1)(x-2)\)