2.6: Ecuaciones cuadráticas
- Page ID
- 116824
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Resolver ecuaciones cuadráticas por factorización.
- Resolver ecuaciones cuadráticas por la propiedad de raíz cuadrada.
- Resuelve ecuaciones cuadráticas completando el cuadrado.
- Resolver ecuaciones cuadráticas usando la fórmula cuadrática.
El monitor de computadora de la izquierda en la Figura\(\PageIndex{1}\) es un modelo de\(23.6\) -inch y el de la derecha es un modelo de\(27\) -inch. Provisiblemente, los monitores parecen muy similares. Si hay una cantidad limitada de espacio y deseamos el monitor más grande posible, ¿cómo decidimos cuál elegir? En esta sección, aprenderemos a resolver problemas como este utilizando cuatro métodos diferentes.

Resolver ecuaciones cuadráticas por factorización
Una ecuación que contiene un polinomio de segundo grado se denomina ecuación cuadrática. Por ejemplo, ecuaciones como\(2x^2 +3x−1=0\) y\(x^2−4= 0\) son ecuaciones cuadráticas. Se utilizan de innumerables maneras en los campos de la ingeniería, la arquitectura, las finanzas, las ciencias biológicas y, por supuesto, las matemáticas.
A menudo, el método más fácil de resolver una ecuación cuadrática es factorizar. Factorizar significa encontrar expresiones que se puedan multiplicar juntas para dar la expresión en un lado de la ecuación.
Si una ecuación cuadrática puede ser factorizada, se escribe como un producto de términos lineales. La resolución por factorización depende de la propiedad de cero producto, que establece que si\(a⋅b=0\), entonces\(a = 0\) o\(b =0\), donde a y b son números reales o expresiones algebraicas. Es decir, si el producto de dos números o dos expresiones es igual a cero, entonces uno de los números o una de las expresiones debe ser igual a cero porque cero multiplicado por cualquier cosa es igual a cero.
Multiplicar los factores expande la ecuación a una cadena de términos separados por signos más o menos. Entonces, en ese sentido, la operación de multiplicación deshace la operación de factorización. Por ejemplo, expanda la expresión\((x−2)(x+3)\) factorizada multiplicando los dos factores juntos.
\[\begin{align*} (x-2)(x+3)&= x^2+3x-2x-6\\ &= x^2+x-6\\ \end{align*}\]
El producto es una expresión cuadrática. Establecer igual a cero,\(x^2+x−6= 0\) es una ecuación cuadrática. Si tuviéramos que factorizar la ecuación, recuperaríamos los factores que multiplicamos.
El proceso de factorizar una ecuación cuadrática depende del coeficiente principal, ya sea que sea\(1\) u otro entero. Veremos ambas situaciones; pero primero, queremos confirmar que la ecuación está escrita en forma estándar,, dónde\(ax^2+bx+c=0\),\(a\)\(b\), y\(c\) son números reales, y\(a≠0\). La ecuación\(x^2 +x−6= 0\) está en forma estándar.
Podemos usar la propiedad de producto cero para resolver ecuaciones cuadráticas en las que primero tenemos que factorizar el mayor factor común (GCF), y para ecuaciones que tienen fórmulas especiales de factorización también, como la diferencia de cuadrados, las cuales veremos más adelante en esta sección.
Los estados de propiedad de producto cero
Si\(a⋅b=0\), entonces\(a=0\) o\(b=0\),
donde\(a\) y\(b\) son números reales o expresiones algebraicas.
Una ecuación cuadrática es una ecuación que contiene un polinomio de segundo grado; por ejemplo
\[ax^2+bx+c=0\]
donde\(a\)\(b\), y\(c\) son números reales, y si\(a≠0\), está en forma normalizada.
Resolviendo Cuadráticas con un Coeficiente Líder de\(1\)
En la ecuación cuadrática\(x^2 +x−6=0\), el coeficiente principal, o el coeficiente de\(x^2\), es\(1\). Tenemos un método para factorizar ecuaciones cuadráticas en esta forma.
- Encuentra dos números cuyo producto sea igual\(c\) y cuya suma sea igual\(b\).
- Usa esos números para escribir dos factores de la forma\((x+k)\) o\((x−k)\), donde k es uno de los números que se encuentran en el paso 1. Usa los números exactamente como están. Es decir, si los dos números son\(1\) y\(−2\), los factores son\((x+1)(x−2)\).
- Resuelve usando la propiedad zero product estableciendo cada factor igual a cero y resolviendo para la variable.
Factorizar y resolver la ecuación:\(x^2+x−6=0\).
Solución
Para factorial\(x^2 +x−6=0\), buscamos dos números cuyo producto sea igual\(−6\) y cuya suma sea igual\(1\). Comience por mirar los posibles factores de\(−6\).
\[1⋅(−6) \nonumber \]
\[(−6)⋅1 \nonumber \]
\[2⋅(−3) \nonumber \]
\[3⋅(−2) \nonumber \]
El último par,\(3⋅(−2)\) suma a\(1\), entonces estos son los números. Tenga en cuenta que solo funcionará un par de números. Después, escribe los factores.
\[(x−2)(x+3)=0 \nonumber \]
Para resolver esta ecuación, utilizamos la propiedad zero product. Establezca cada factor igual a cero y resuelva.
\[\begin{align*} (x-2)(x+3)&= 0\\ (x-2)&= 0\\ x&= 2\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
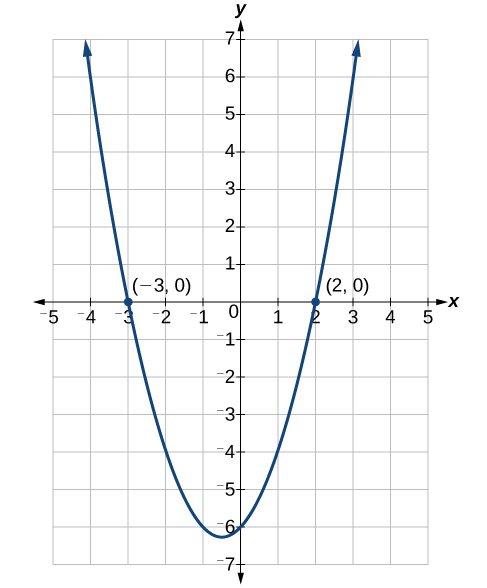
Las dos soluciones son\(2\) y\(−3\). Podemos ver cómo se relacionan las soluciones con la gráfica de la Figura\(\PageIndex{2}\). Las soluciones son las intercepciones x de\(x^2 +x−6=0\).
Factorizar y resolver la ecuación cuadrática:\(x^2−5x−6=0\).
- Contestar
-
\((x−6)(x+1)=0\),\(x=6\),\(x=−1\)
Resolver la ecuación cuadrática factorizando:\(x^2+8x+15=0\).
Solución
Encuentra dos números cuyo producto sea igual\(15\) y cuya suma sea igual\(8\). Enumerar los factores de\(15\).
\[1⋅15 \nonumber \]
\[3⋅5 \nonumber \]
\[(−1)⋅(−15) \nonumber \]
\[(−3)⋅(−5) \nonumber \]
Los números que se suman a\(8\) son\(3\) y\(5\). Luego, escribe los factores, establece cada factor igual a cero y resuelve.
\[\begin{align*} (x+3)(x+5)&= 0\\ (x+3)&= 0\\ x&= -3\\ (x+5)&= 0\\ x&= -5 \end{align*}\]
Las soluciones son\(−3\) y\(−5\).
Resolver la ecuación cuadrática factorizando:\(x^2−4x−21=0\).
- Contestar
-
\((x−7)(x+3)=0\),\(x=7\),\(x=−3\)
Resuelve la ecuación de diferencia de cuadrados usando la propiedad de cero producto:\(x^2−9=0\).
Solución
Reconociendo que la ecuación representa la diferencia de cuadrados, podemos escribir los dos factores tomando la raíz cuadrada de cada término, usando un signo menos como operador en un factor y un signo más como operador en el otro. Resuelve usando la propiedad de factor cero.
\[\begin{align*} x^2-9&= 0\\ (x-3)(x+3)&= 0\\ x-3&= 0\\ x&= 3\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
Las soluciones son\(3\) y\(−3\).
Resolver factorizando:\(x^2−25=0\).
- Contestar
-
\((x+5)(x−5)=0, x=−5, x=5\)
Factorización y Resolución de una Ecuación Cuadrática de Orden Superior
Cuando el coeficiente principal no lo es\(1\), factorizamos una ecuación cuadrática utilizando el método llamado agrupación, que requiere cuatro términos.
Con la ecuación en forma estándar, revisemos los procedimientos de agrupación
- Con la cuadrática en forma estándar,\(ax^2+bx+c=0\), multiplicar\(a⋅c\).
- Encuentra dos números cuyo producto sea igual a ac y cuya suma sea igual\(b\).
- Reescribe la ecuación reemplazando el\(bx\) término con dos términos usando los números encontrados en paso\(1\) como coeficientes de\(x\).
- Factorizar los dos primeros términos y luego factorizar los dos últimos términos. Las expresiones entre paréntesis deben ser exactamente las mismas para usar agrupación.
- Factorizar la expresión entre paréntesis.
- Establezca las expresiones iguales a cero y resuelva para la variable.
Utilice la agrupación para factorizar y resolver la ecuación cuadrática:\(4x^2+15x+9=0\).
Solución
Primero, multiplicar\(ac:4(9)=36\). Luego enumere los factores de\(36\).
\[1⋅36 \nonumber\]
\[2⋅18 \nonumber\]
\[3⋅12 \nonumber\]
\[4⋅9 \nonumber\]
\[6⋅6 \nonumber\]
El único par de factores que suma a\(15\) es\(3+12\). Reescribir la ecuación reemplazando el término b,\(15x\), con dos términos usando\(3\) y\(12\) como coeficientes de\(x\). Factorizar los dos primeros términos, y luego factorizar los dos últimos términos.
\[\begin{align*} 4x^2+3x+12x+9&= 0\\ x(4x+3)+3(4x+3)&= 0\\ (4x+3)(x+3)&= 0 \qquad \text{Solve using the zero-product property}\\ (4x+3)&= 3\\ x&= -\dfrac{3}{4}\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
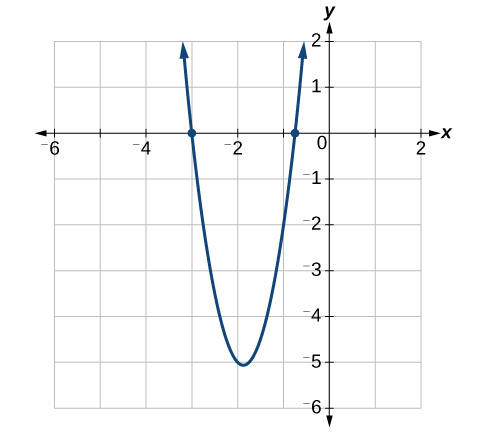
Las soluciones son\(−\dfrac{3}{4}\), y\(−3\). Ver Figura\(\PageIndex{3}\).
Resolver usando factorización agrupando:\(12x^2+11x+2=0\).
- Contestar
-
\((3x+2)(4x+1)=0\),\(x=−\dfrac{2}{3}\),\(x=−\dfrac{1}{4}\)
Resolver la ecuación factorizando:\(−3x^3−5x^2−2x=0\).
Solución
Esta ecuación no parece cuadrática, como lo es el poder más alto\(3\), no\(2\). Recordemos que lo primero que queremos hacer al resolver cualquier ecuación es factorizar el GCF, si existe. Y lo hace aquí. Podemos factorizar\(−x\) de todos los términos y luego proceder a la agrupación.
\ [\ begin {align*}
-3x^3-5x^2-2x&= 0\\
-x (3x^2+5x+2) &= 0\\
-x (3x^2+3x+2x+2) &= 0\ qquad\ text {Usa agrupación en la expresión entre paréntesis}\\
-x [3x (x+1) +2 (x+1)] &= 0\\
-x (3x+2) (x+1) (x+1)) &= 0\
\\ text {Ahora, usamos la propiedad de producto cero. Observe que tenemos tres factores.} \\
-x&= 0\\
x&= 0\\
3x+2&= 0\\
x&= -\ dfrac {2} {3}\\
x+1&= 0\\
x&= -1
\ final {alinear*}\]
Las soluciones son\(0\),\(−\dfrac{2}{3}\), y\(−1\).
Resolver factorizando:\(x^3+11x^2+10x=0\).
- Contestar
-
\(x=0, x=−10, x=−1\)
Uso de la propiedad Raíz Cuadrada
Cuando no hay término lineal en la ecuación, otro método para resolver una ecuación cuadrática es mediante el uso de la propiedad raíz cuadrada, en la que aislamos el\(x^2\) término y tomamos la raíz cuadrada del número en el otro lado del signo igual. Hay que tener en cuenta que a veces podemos tener que manipular la ecuación para aislar el\(x^2\) término y así poder utilizar la propiedad raíz cuadrada.
Con el\(x^2\) término aislado, la propiedad de raíz cuadrada establece que:
donde\(k\) es un número real distinto de cero.
- Aislar el\(x^2\) término en un lado del signo igual.
- Tomar la raíz cuadrada de ambos lados de la ecuación, poniendo un\(±\) signo antes de la expresión en el lado opuesto al término cuadrado.
- Simplifica los números en el costado con el\(±\) letrero.
Resolver la cuadrática usando la propiedad raíz cuadrada:\(x^2=8\).
Solución
Toma la raíz cuadrada de ambos lados, y luego simplifica el radical. Recuerda usar un\(±\) signo antes del símbolo radical.
\[\begin{align*} x^2&= 8\\ x&= \pm \sqrt{8}\\ &= \pm 2\sqrt{2} \end{align*}\]
Las soluciones son\(2\sqrt{2}\),\(-2\sqrt{2}\)
Resolver la ecuación cuadrática:\(4x^2+1=7\).
Solución
Primero, aislar el\(x^2\) término. Después tomar la raíz cuadrada de ambos lados.
\[\begin{align*} 4x^2+1&= 7\\ 4x^2&= 6\\ x^2&= \dfrac{6}{4}\\ x&= \pm \dfrac{\sqrt{6}}{2} \end{align*}\]
Las soluciones son\(\dfrac{\sqrt{6}}{2}\), y\(-\dfrac{\sqrt{6}}{2}\).
Resuelve la ecuación cuadrática usando la propiedad raíz cuadrada:\(3{(x−4)}^2=15\).
- Contestar
-
\(x=4±\sqrt{5}\)
Completando la Plaza
No todas las ecuaciones cuadráticas pueden ser factorizadas o pueden resolverse en su forma original usando la propiedad raíz cuadrada. En estos casos, podemos usar un método para resolver una ecuación cuadrática conocida como completar el cuadrado. Usando este método, sumamos o restamos términos a ambos lados de la ecuación hasta que tengamos un trinomio cuadrado perfecto en un lado del signo igual. Luego aplicamos la propiedad de raíz cuadrada. Para completar el cuadrado, el coeficiente principal,\(a\), debe ser igual\(1\). Si no lo hace, entonces divide la ecuación completa por\(a\). Entonces, podemos usar los siguientes procedimientos para resolver una ecuación cuadrática completando el cuadrado.
Utilizaremos el ejemplo\(x^2+4x+1=0\) para ilustrar cada paso.
Dada una ecuación cuadrática que no se puede factorizar, y con\(a=1\), first add or subtract the constant term to the right sign of the equal sign.
\ [\ begin {align*}
x^2+4x+1&= 0\\
x^2+4x&= -1\ qquad\ text {Multiplicar el b}\ texto {término por}\ dfrac {1} {2}\ texto {y cuadrarlo.} \\
\ dfrac {1} {2} (4) &= 2\\
2^2&= 4\ qquad\ text {Agregar}\ left ({\ dfrac {1} {2}}\ right) ^2\ text {a ambos lados del signo igual y simplificar el lado derecho. Tenemos}\\
x^2+4x+4&= -1+4\\
x^2+4x+4&= 3\ qquad\ text {El lado izquierdo de la ecuación ahora se puede factorizar como un cuadrado perfecto.} \\
{(x+2)} ^2&=3\\
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\ qquad\ text {Usa la propiedad raíz cuadrada y resuelve.} \\
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\\
x+2&=\ pm\ sqrt {3}\\
x&= -2\ pm\ sqrt {3}
\ final {alinear*}\]
Las soluciones son\(−2+\sqrt{3}\), y\(−2−\sqrt{3}\).
Resuelve la ecuación cuadrática completando el cuadrado:\(x^2−3x−5=0\).
Solución
Primero, mover el término constante al lado derecho del signo igual.
\ [\ begin {align*}
x^2-3x&= 5\ qquad\ text {Entonces, toma}\ dfrac {1} {2}\ texto {del término b y cuadrarlo.} \\
\ dfrac {1} {2} (-3) &= -\ dfrac {3} {2}\\
{\ izquierda (-\ dfrac {3} {2}\ derecha)} ^2=\ dfrac {9} {4}\
x^2-3x+ {\ left (-\ dfrac {3} {2}\ derecha)} ^2&= 5+ {\ left (-\ dfrac {3} {2}\ right)} ^2\ qquad\ text {Agrega el resultado a ambos lados del signo igual.} \\
x^2-3x+\ dfrac {9} {4} &= 5+\ dfrac {9} {4}\\
\ text {Factorizar el lado izquierdo como un cuadrado perfecto y simplificar el lado derecho.} \\
{\ left (x-\ dfrac {3} {2}\ derecha)} ^2&=\ dfrac {29} {4}\\
(x-\ dfrac {3} {2}) &=\ pm\ dfrac {\ sqrt {29}} {2}\ qquad\ text {Usa la propiedad raíz cuadrada y resuelve.} \\
x&=\ dfrac {3} {2}\ pm\ dfrac {\ sqrt {29}} {2}\
\ final {alinear*}\]
Las soluciones son\(\dfrac{3}{2}+\dfrac{\sqrt{29}}{2}\), y\(\dfrac{3}{2}-\dfrac{\sqrt{29}}{2}\)
Resuelve completando la plaza:\(x^2−6x=13\).
- Contestar
-
\(x=3±\sqrt{22}\)
Uso de la Fórmula Cuadrática
El cuarto método para resolver una ecuación cuadrática es mediante el uso de la fórmula cuadrática, una fórmula que resolverá todas las ecuaciones cuadráticas. Aunque la fórmula cuadrática funciona en cualquier ecuación cuadrática en forma estándar, es fácil cometer errores al sustituir los valores en la fórmula. Preste mucha atención al sustituir y use paréntesis al insertar un número negativo.
Podemos derivar la fórmula cuadrática completando el cuadrado. Supondremos que el coeficiente principal es positivo; si es negativo, podemos multiplicar la ecuación por\(−1\) y obtener una a positiva Dado\(ax^2+bx+c=0, a≠0\), completaremos el cuadrado de la siguiente manera:
Primero, mueve el término constante hacia el lado derecho del signo igual:
\[ax^2+bx=−c \nonumber \]
Como queremos que el coeficiente principal sea igual\(1\), dividirlo por\(a\):
\[x^2+\dfrac{b}{a}x=−\dfrac{c}{a} \nonumber \]
Luego, encuentra\(\dfrac{1}{2}\) del término medio, y agrega\({(\dfrac{1}{2}\dfrac{b}{a})}^2=\dfrac{b^2}{4a^2}\) a ambos lados del signo igual:
\[x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}=\dfrac{b^2}{4a^2}-\dfrac{c}{a} \nonumber \]
A continuación, escribe el lado izquierdo como un cuadrado perfecto. Encuentra el denominador común del lado derecho y escríbalo como una sola fracción:
\[{(x+\dfrac{b}{2a})}^2=\dfrac{b^2-4ac}{4a^2} \nonumber \]
Ahora, use la propiedad de raíz cuadrada, que da
\[x+\dfrac{b}{2a}=±\sqrt{\dfrac{b^2-4ac}{4a^2}} \nonumber \]
\[x+\dfrac{b}{2a}=\dfrac{±\sqrt{b^2-4ac}}{2a} \nonumber \]
Por último,\(-\dfrac{b}{2a}\) sumar a ambos lados de la ecuación y combinar los términos en el lado derecho. Por lo tanto,
\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \nonumber \]
Escrito en forma estándar,\(ax^2+bx+c=0\), cualquier ecuación cuadrática se puede resolver usando la fórmula cuadrática:
\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}\]donde\(a\),\(b\), y\(c\) son números reales y\(a≠0\).
Dada una ecuación cuadrática, resuelva usando la fórmula cuadrática
- Asegúrese de que la ecuación esté en forma estándar:\(ax^2+bx+c=0\).
- Tomar nota de los valores de los coeficientes y término constante,\(a\),\(b\), y\(c\).
- Sustituir cuidadosamente los valores señalados en el paso 2 en la ecuación. Para evitar errores innecesarios, use paréntesis alrededor de cada entrada numérica en la fórmula.
- Calcular y resolver.
Resolver la ecuación cuadrática:\(x^2+5x+1=0\).
Solución
Identificar los coeficientes:\(a=1,b=5,c=1\). Luego usa la fórmula cuadrática.
\[\begin{align*} x&= \dfrac{-(5) \pm \sqrt{(5)^2-4(1)(1)}}{2(1)}\\ &= \dfrac{-5 \pm \sqrt{25-4}}{2}\\ &= \dfrac{-5 \pm \sqrt{21}}{2} \end{align*}\]
Usa la fórmula cuadrática para resolver\(x^2+x+2=0\).
Solución
Primero, identificamos los coeficientes:\(a=1\),\(b=1\), y\(c=2\).
Sustituir estos valores en la fórmula cuadrática.
\[\begin{align*} x&= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\ &= \dfrac{-(1) \pm \sqrt{(1)^2-4(1)(2)}}{2(1)}\\ &= \dfrac{-1 \pm \sqrt{1-8}}{2}\\ &= \dfrac{-1 \pm \sqrt{-7}}{2}\\ &= \dfrac{-1 \pm i\sqrt{7}}{2} \end{align*}\]
Resuelve la ecuación cuadrática usando la fórmula cuadrática:\(9x^2+3x−2=0\).
- Contestar
-
\(x=-\dfrac{2}{3},x=\dfrac{1}{3}\)
El discriminante
La fórmula cuadrática no sólo genera las soluciones a una ecuación cuadrática, nos habla de la naturaleza de las soluciones cuando consideramos lo discriminante, o la expresión bajo el radical,\(b^2−4ac\). El discriminante nos dice si las soluciones son números reales o números complejos, y cuántas soluciones de cada tipo esperar. Tabla\(\PageIndex{1}\) relaciona el valor del discriminante con las soluciones de una ecuación cuadrática.
| Valor de discriminante | Resultados |
|---|---|
| \(b^2−4ac=0\) | Una solución racional (solución doble) |
| \(b^2−4ac>0\), cuadrado perfecto | Dos soluciones racionales |
| \(b^2−4ac>0\), no es un cuadrado perfecto | Dos soluciones irracionales |
| \(b^2−4ac<0\) | Dos soluciones complejas |
Porque\(ax^2+bx+c=0\), donde\(a\)\(b\), y\(c\) son números reales, el discriminante es la expresión bajo el radical en la fórmula cuadrática:\(b^2−4ac\). Nos dice si las soluciones son números reales o números complejos y cuántas soluciones de cada tipo esperar.
Utilice el discriminante para encontrar la naturaleza de las soluciones a las siguientes ecuaciones cuadráticas:
- \(x^2+4x+4=0\)
- \(8x^2+14x+3=0\)
- \(3x^2−5x−2=0\)
- \(3x^2−10x+15=0\)
Solución
Calcular el discriminante\(b^2−4ac\) para cada ecuación e indicar el tipo de soluciones esperadas.
a.
\(x^2+4x+4=0\)
\(b^2-4ac={(4)}^2-4(1)(4)=0\)Habrá una solución doble racional.
b.
\(8x^2+14x+3=0\)
\(b^2-4ac={(14)}^2-4(8)(3)=100\)Al\(100\) ser un cuadrado perfecto, habrá dos soluciones racionales.
c.
\(3x^2−5x−2=0\)
\(b^2-4ac={(-5)}^2-4(3)(-2)=49\)Al\(49\) ser un cuadrado perfecto, habrá dos soluciones racionales.
d.
\(3x^2−10x+15=0\)
\(b^2-4ac={(-10)}^2-4(3)(15)=-80\)Habrá dos soluciones complejas.
Usando el Teorema de Pitágoras
Una de las fórmulas más famosas en matemáticas es el Teorema de Pitágoras. Se basa en un triángulo rectángulo, y establece la relación entre las longitudes de los lados como\(a^2+b^2=c^2\), donde\(a\) y\(b\) se refieren a las patas de un triángulo rectángulo adyacente al\(90°\) ángulo, y\(c\) se refiere a la hipotenusa. Tiene usos inconmensurables en arquitectura, ingeniería, ciencias, geometría, trigonometría y álgebra, y en aplicaciones cotidianas.
Utilizamos el Teorema de Pitágoras para resolver la longitud de un lado de un triángulo cuando tenemos las longitudes de los otros dos. Porque cada uno de los términos es cuadrado en el teorema, cuando estamos resolviendo para un lado de un triángulo, tenemos una ecuación cuadrática. Podemos usar los métodos para resolver ecuaciones cuadráticas que aprendimos en esta sección para resolver por el lado faltante.
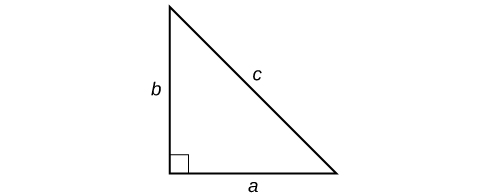
El Teorema de Pitágoras se da como
\[a^2+b^2=c^2\]
donde\(a\) y\(b\) se refieren a las patas de un triángulo rectángulo adyacente al\(90°\) ángulo, y\(c\) se refiere a la hipotenusa, como se muestra en.
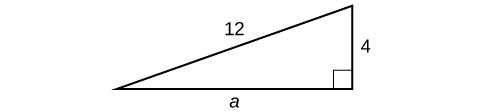
Encuentra la longitud del lado faltante del triángulo rectángulo en la Figura\(\PageIndex{5}\).
Solución
Como tenemos mediciones para lado\(b\) y la hipotenusa, el lado faltante es\(a\).
\[\begin{align*} a^2+b^2&= c^2\\ a^2+{(4)}^2&= {(12)}^2\\ a^2+16&= 144\\ a^2&= 128\\ a&= \sqrt{128}\\ &= 8\sqrt{2} \end{align*}\]
Usa el Teorema de Pitágoras para resolver el problema del triángulo rectángulo: La pierna a mide 4 unidades, la pierna b mide 3 unidades. Encuentra la longitud de la hipotenusa.
- Contestar
-
\(5\)unidades
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con ecuaciones cuadráticas.
- Resolver ecuaciones cuadráticas por factorización
- La propiedad de producto cero
- Completando la Plaza
- Fórmula cuadrática con dos soluciones racionales
- Longitud de una pata de un triángulo rectángulo
Ecuaciones Clave
| fórmula cuadrática | \(x=\dfrac{−b±\sqrt{b^2-4ac}}{2a}\) |
Conceptos clave
- Muchas ecuaciones cuadráticas se pueden resolver factorizando cuando la ecuación tiene un coeficiente inicial de\(1\) o si la ecuación es una diferencia de cuadrados. La propiedad de factor cero se utiliza entonces para encontrar soluciones. Ver Ejemplo, Ejemplo y Ejemplo.
- Muchas ecuaciones cuadráticas con un coeficiente principal distinto al que se\(1\) pueden resolver factorizando usando el método de agrupación. Ver Ejemplo y Ejemplo.
- Otro método para resolver cuadráticas es la propiedad de raíz cuadrada. La variable es cuadrada. Aislamos el término cuadrado y tomamos la raíz cuadrada de ambos lados de la ecuación. La solución dará una solución positiva y negativa. Ver Ejemplo y Ejemplo.
- Completar el cuadrado es un método para resolver ecuaciones cuadráticas cuando la ecuación no puede ser factorizada. Ver Ejemplo.
- Un método altamente confiable para resolver ecuaciones cuadráticas es la fórmula cuadrática, basada en los coeficientes y el término constante en la ecuación. Ver Ejemplo.
- El discriminante se utiliza para indicar la naturaleza de las raíces que producirá la ecuación cuadrática: reales o complejas, racionales o irracionales, y cuántas de cada una. Ver Ejemplo.
- El Teorema de Pitágoras, entre los teoremas más famosos de la historia, se utiliza para resolver problemas de triángulo rectángulo y tiene aplicaciones en numerosos campos. Resolver la longitud de un lado de un triángulo rectángulo requiere resolver una ecuación cuadrática. Ver Ejemplo.


