3.8: Funciones inversas

Objetivos de aprendizaje

• Verificar funciones inversas.
• Determinar el dominio y el rango de una función inversa, y restringir el dominio de una función para hacerla uno a uno.
• Encontrar o evaluar la inversa de una función.
• Utilice la gráfica de una función uno a uno para graficar su función inversa en los mismos ejes.

Una bomba de calor reversible es un sistema de control de clima que es un acondicionador de aire y un calentador en un solo dispositivo. Operado en una dirección, bombea calor fuera de una casa para proporcionar enfriamiento. Operando a la inversa, bombea calor al edificio desde el exterior, incluso en climas fríos, para proporcionar calefacción. Como calentador, una bomba de calor es varias veces más eficiente que el calentamiento por resistencia eléctrica convencional.

Si algunas máquinas físicas pueden funcionar en dos direcciones, podríamos preguntarnos si algunas de las funciones “máquinas” que hemos estado estudiando también pueden correr hacia atrás. La figura\(\PageIndex{1}\) proporciona una representación visual de esta pregunta. En esta sección, consideraremos la naturaleza inversa de las funciones.

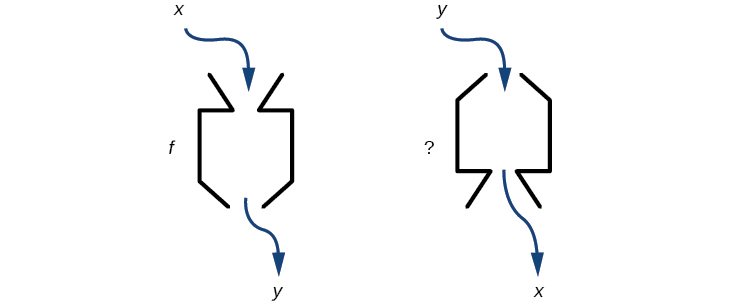
Figura\(\PageIndex{1}\): ¿Puede una función “máquina” operar en reversa?

Verificación de que dos funciones son funciones inversas

Supongamos que un diseñador de moda que viaja a Milán para un desfile de modas quiere saber cuál será la temperatura. No está familiarizado con la escala Celsius. Para hacerse una idea de cómo se relacionan las mediciones de temperatura, le pide a su asistente, Betty, que convierta 75 grados Fahrenheit a grados Celsius. Ella encuentra la fórmula

\[C=\dfrac{5}{9}(F−32)\]

y sustitutos 75\(F\) para calcular

\[\dfrac{5}{9}(75−32)\approx24^{\circ}\]

Sabiendo que un cómodo 75 grados Fahrenheit es de unos 24 grados Celsius, envía a su asistente el pronóstico meteorológico de la semana desde Figura\(\PageIndex{2}\) para Milán, y le pide que convierta todas las temperaturas a grados Fahrenheit.

Figura\(\PageIndex{2}\): Un pronóstico del clima de lunes a jueves.

Al principio, Betty considera usar la fórmula que ya encontró para completar las conversiones. Después de todo, conoce su álgebra, y puede resolver fácilmente la ecuación\(F\) después de sustituir un valor por\(C\). Por ejemplo, para convertir 26 grados centígrados, podría escribir

\[\begin{align} 26&=\dfrac{5}{9}(F-32) \\ 26⋅\dfrac{9}{5}&=F−32 \\ F&=26⋅\dfrac{9}{5}+32\approx79\end{align}\]

Después de considerar por un momento esta opción, sin embargo, se da cuenta de que resolver la ecuación para cada una de las temperaturas será muy tedioso. Se da cuenta que dado que la evaluación es más fácil que resolver, sería mucho más conveniente tener una fórmula diferente, una que tome la temperatura Celsius y produzca la temperatura Fahrenheit.

La fórmula para la que Betty está buscando corresponde a la idea de una función inversa, que es una función para la cual la entrada de la función original se convierte en la salida de la función inversa y la salida de la función original se convierte en la entrada de la función inversa.

Dada una función\(f(x)\), representamos su inverso como\(f^{−1}(x)\), leído como “\(f\)inverso de”\(x\). El elevado −1 es parte de la notación. No es un exponente; no implica una potencia de −1. En otras palabras,\(f^{−1}(x)\) no significa\(\frac{1}{f(x)}\) porque\(\frac{1}{f(x)}\) es el recíproco de\(f\) y no lo inverso.

La notación “similar a un exponente” proviene de una analogía entre la composición de la función y la multiplicación: así como\(a^{−1}a=1\) (1 es el elemento de identidad para la multiplicación) para cualquier número distinto de cero\(a\), así es\(f^{−1}{\circ}f\) igual a la función de identidad, es decir,

\[(f^{−1}{\circ}f)(x)=f^{−1}(f(x))=f^{−1}(y)=x\]

Esto es válido para todos\(x\) en el dominio de\(f\). Informalmente, esto significa que las funciones inversas se “deshacen” entre sí. Sin embargo, así como cero no tiene un recíproco, algunas funciones no tienen inversas.

Dada una función\(f(x)\), podemos verificar si alguna otra función\(g(x)\) es la inversa de\(f(x)\) comprobando si alguna\(g(f(x))=x\) o\(f(g(x))=x\) es verdadera. Podemos probar cualquier ecuación con la que sea más conveniente trabajar porque son lógicamente equivalentes (es decir, si una es verdadera, entonces también lo es la otra).

Por ejemplo,\(y=4x\) y\(y=\frac{1}{4}x\) son funciones inversas.

\[(f^{−1}{\circ}f)(x)=f^{-1}(4x)=\dfrac{1}{4}(4x)=x\]

y

\[(f{\circ}f^{−1})(x)=f\Big(\dfrac{1}{4}x\Big)=4\Big(\dfrac{1}{4}x\Big)=x\]

Algunos pares de coordenadas de la gráfica de la función\(y=4x\) son\((−2, −8)\),\((0, 0)\), y\((2, 8)\). Algunos pares de coordenadas de la gráfica de la función\(y=\frac{1}{4}x\) son\((−8, −2)\),\((0, 0)\), y\((8, 2)\). Si intercambiamos la entrada y salida de cada par de coordenadas de una función, los pares de coordenadas intercambiadas aparecerían en la gráfica de la función inversa.

Definición: Función inversa

Para cualquier función uno a uno\(f(x)=y\), una función\(f^{−1}(x)\) es una función inversa de\(f\) if\(f^{−1}(y)=x\). Esto también se puede escribir como\(f^{−1}(f(x))=x\) para todos\(x\) en el dominio de\(f\). También se deduce que\(f(f^{−1}(x))=x\) para todos\(x\) en el dominio de\(f^{−1}\) si\(f^{−1}\) es la inversa de\(f\).

La notación\(f^{−1}\) se lee “\(f\)inversa”. Como cualquier otra función, podemos usar cualquier nombre de variable como entrada para\(f^{−1}\), así que a menudo escribiremos\(f^{−1}(x)\), que leemos como “\(f\)inverso de”\(x\). Tenga en cuenta que

\[f^{−1}(x)\neq\dfrac{1}{f(x)}\]

y no todas las funciones tienen inversas.

Ejemplo\(\PageIndex{1}\): Identifying an Inverse Function for a Given Input-Output Pair

Si para una función particular uno a uno\(f(2)=4\) y\(f(5)=12\), ¿cuáles son los valores de entrada y salida correspondientes para la función inversa?

Solución

La función inversa invierte las cantidades de entrada y salida, así que si

\[f(2)=4, \text{ then } f^{-1}(4)=2 ;\\ f(5)=12, \text{ then }f^{-1}(12)=5\].

Alternativamente, si queremos nombrar la función inversa\(g\), entonces\(g(4)=2\) y\(g(12)=5\).

Análisis

Observe que si mostramos los pares de coordenadas en forma de tabla, la entrada y la salida se invierten claramente. Ver Tabla\(\PageIndex{1}\).

Mesa\(\PageIndex{1}\)

\((x,f(x))\)	\((x,g(x))\)
\ ((x, f (x))\)” style="vertical-align:middle; text-align:center; ">\((2,4)\)	\ ((x, g (x))\)” style="vertical-align:middle; text-align:center; ">\((4,2)\)
\ ((x, f (x))\)” style="vertical-align:middle; text-align:center; ">\((5,12)\)	\ ((x, g (x))\)” style="vertical-align:middle; text-align:center; ">\((12,5)\)

Ejercicio\(\PageIndex{1}\)

Dado eso\(h^{-1}(6)=2\), ¿cuáles son los valores de entrada y salida correspondientes de la función original\(h\)?

Contestar

\(h(2)=6\)

Cómo: Dadas dos funciones\(f(x)\) and \(g(x)\), test whether the functions are inverses of each other.

1. Determinar si\(f(g(x))=x\) o\(g(f(x))=x\).
2. Si ambas afirmaciones son verdaderas, entonces\(g=f^{-1}\) y\(f=g^{-1}\). Si alguna declaración es falsa, entonces ambas son falsas, y\(g{\neq}f^{-1}\) y\(f{\neq}g^{-1}\).

Ejemplo\(\PageIndex{2}\): Testing Inverse Relationships Algebraically

Si\(f(x)=\frac{1}{x+2}\) y\(g(x)=\frac{1}{x}−2\), ¿es\(g=f^{-1}\)?

Solución

\[\begin{align} g(f(x))&=\dfrac{1}{(\frac{1}{x+2})−2} \\ &=x+2−2 \\&=x \end{align}\]

entonces

\[g=f^{-1} \text{ and } f=g^{-1}\]

Esto es suficiente para responder sí a la pregunta, pero también podemos verificar la otra fórmula.

\[\begin{align} f(g(x))&=\dfrac{1}{\frac{1}{x}-2+2} \\ &= \dfrac{1}{\frac{1}{x}} \\ &=x \end{align}\]

Análisis

Observe que las operaciones inversas están en orden inverso a las operaciones de la función original.

Ejercicio\(\PageIndex{2}\)

Si\(f(x)=x^3−4\) y\(g(x)=\sqrt[3]{x+4}\), ¿es\(g=f^{-1}\)?

Contestar

Sí

Ejemplo\(\PageIndex{3}\): Determining Inverse Relationships for Power Functions

Si\(f(x)=x^3\) (la función de cubo) y\(g(x)=\frac{1}{3}x\),\(g=f^{-1}\) ¿es?

Solución

\[f(g(x))=\dfrac{x^3}{27}{\neq}x\]

No, las funciones no son inversas.
Análisis

La inversa correcta al cubo es, por supuesto, la raíz cubo\(\sqrt[3]{x}=x^{\frac{1}{3}}\), es decir, la tercera parte es un exponente, no un multiplicador.

Ejercicio\(\PageIndex{3}\)

Si\(f(x)=(x−1)^3\) y\(g(x)=\sqrt[3]{x}+1\), ¿es\(g=f^{-1}\)?

Contestar

Sí

Búsqueda de dominio y rango de funciones inversas

Las salidas de la función\(f\) son las entradas a\(f^{-1}\), por lo que el rango de\(f\) es también el dominio de\(f^{-1}\). Asimismo, debido a que las entradas a\(f\) son las salidas de\(f^{-1}\), el dominio de\(f\) es el rango de\(f^{-1}\). Podemos visualizar la situación como en la Figura\(\PageIndex{3}\).

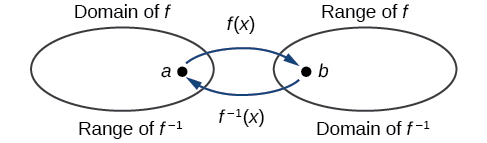
Figura\(\PageIndex{3}\): Dominio y rango de una función y su inversa.

Cuando una función no tiene función inversa, es posible crear una nueva función donde esa nueva función en un dominio limitado tiene una función inversa. Por ejemplo, lo inverso de\(f(x)=\sqrt{x}\) es\(f^{-1}(x)=x^2\), porque un cuadrado “deshace” una raíz cuadrada; pero el cuadrado es sólo el inverso de la raíz cuadrada en el dominio\(\left[0,\infty\right)\), ya que ese es el rango de\(f(x)=\sqrt{x}\).

Podemos ver este problema desde el otro lado, comenzando con la función cuadrada (cuadrática del kit de herramientas)\(f(x)=x^2\). Si queremos construir una inversa a esta función, nos encontramos con un problema, porque por cada salida dada de la función cuadrática, hay dos entradas correspondientes (excepto cuando la entrada es 0). Por ejemplo, la salida 9 de la función cuadrática corresponde a las entradas 3 y —3. Pero una salida de una función es una entrada a su inversa; si esta entrada inversa corresponde a más de una salida inversa (entrada de la función original), ¡entonces la “inversa” no es una función en absoluto! Para decirlo de otra manera, la función cuadrática no es una función uno a uno; falla la prueba de línea horizontal, por lo que no tiene una función inversa. Para que una función tenga una inversa, debe ser una función uno a uno.

En muchos casos, si una función no es uno a uno, todavía podemos restringir la función a una parte de su dominio en el que es uno a uno. Por ejemplo, podemos hacer una versión restringida de la función square\(f(x)=x^2\) con su rango limitado a\(\left[0,\infty\right)\), que es una función uno a uno (pasa la prueba de línea horizontal) y que tiene una inversa (la función de raíz cuadrada).

Si está\(f(x)=(x−1)^2\) encendido\([1,∞)\), entonces la función inversa es\(f^{-1}(x)=\sqrt{x}+1\).

• El dominio de\(f\) = rango de\(f^{-1} = \left[1,\infty\right)\).
• El dominio de\(f^{-1}\) = rango de\(f = \left[0,\infty\right)\).

¿Es posible que una función tenga más de una inversa?

No. Si dos funciones supuestamente diferentes, digamos,\(g\) y h, ambas cumplen con la definición de ser inversas de otra función\(f\), entonces puedes probarlo\(g=h\). Acabamos de ver que algunas funciones solo tienen inversas si restringimos el dominio de la función original. En estos casos, puede haber más de una manera de restringir el dominio, dando lugar a diferentes inversos. Sin embargo, en cualquier dominio, la función original todavía tiene una única inversa.

Nota: Dominio y rango de funciones inversas

El rango de una función\(f(x)\) es el dominio de la función inversa\(f^{-1}(x)\).

El dominio de\(f(x)\) es el rango de\(f^{-1}(x)\).

Cómo: Dada una función, encontrar el dominio y rango de su inversa.

1. Si la función es uno a uno, escriba el rango de la función original como el dominio de la inversa, y escriba el dominio de la función original como el rango de la inversa.
2. Si el dominio de la función original necesita ser restringido para hacerlo uno a uno, entonces este dominio restringido se convierte en el rango de la función inversa.

Ejemplo\(\PageIndex{4}\): Finding the Inverses of Toolkit Functions

Identifica cuáles de las funciones del kit de herramientas además de la función cuadrática no son uno-a-uno, y encuentra un dominio restringido en el que cada función es uno a uno, si corresponde. Las funciones del kit de herramientas se revisan en la Tabla\(\PageIndex{2}\). Restringiremos el dominio de tal manera que la función asume todos los valores y exactamente una vez.

Mesa\(\PageIndex{2}\)

Constante	Identidad	Cuadrático	Cúbico	recíproco
\(f(x)=c\)	\(f(x)=x\)	\(f(x)=x^2\)	\(f(x)=x^3\)	\(f(x)=\frac{1}{x}\)
Recíproco al cuadrado	Raíz cúbica	Raíz cuadrada	Valor Absoluto
\(f(x)=\frac{1}{x^2}\)	\(f(x)=\sqrt[3]{x}\)	\(f(x)=\sqrt{x}\)	\(f(x)=|x|\)

Solución

La función constante no es uno a uno, y no hay dominio (excepto un solo punto) en el que pueda ser uno a uno, por lo que la función constante no tiene un inverso significativo.

La función de valor absoluto puede restringirse al dominio\(\left[0,\infty\right)\), donde es igual a la función de identidad.

La función reciprocal-cuadrada puede restringirse al dominio\((0,\infty)\).

Análisis

Podemos ver que estas funciones (si no están restringidas) no son una a una al mirar sus gráficas, que se muestran en la Figura\(\PageIndex{4}\). Ambos fallarían en la prueba de línea horizontal. Sin embargo, si una función está restringida a un determinado dominio para que pase la prueba de línea horizontal, entonces en ese dominio restringido, puede tener una inversa.

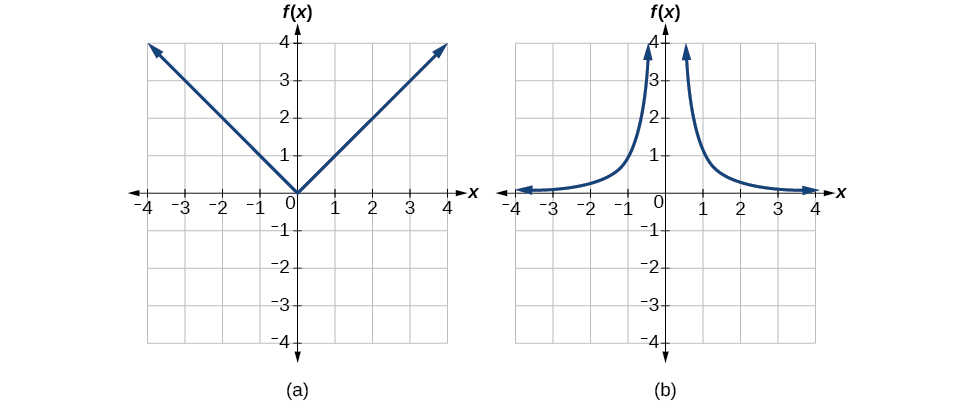
Figura\(\PageIndex{4}\): (a) Valor absoluto (b) Recíproco al cuadrado

\(\PageIndex{4}\): El dominio de la función\(f\) es\((1,\infty)\) y el rango de función\(f\) es\((−\infty,−2)\). Encuentra el dominio y el rango de la función inversa.

Solución

El dominio de la función\(f^{-1}\) es\((−\infty,−2)\) y el rango de función\(f^{-1}\) es\((1,\infty)\).

Encontrar y evaluar funciones inversas

Una vez que tenemos una función uno a uno, podemos evaluar su inversa en entradas de función inversa específicas o construir una representación completa de la función inversa en muchos casos.

Invertir funciones tabulares

Supongamos que queremos encontrar la inversa de una función representada en forma de tabla. Recuerde que el dominio de una función es el rango de la inversa y el rango de la función es el dominio de la inversa. Entonces necesitamos intercambiar el dominio y el rango.

Cada fila (o columna) de entradas se convierte en la fila (o columna) de salidas para la función inversa. Del mismo modo, cada fila (o columna) de salidas se convierte en la fila (o columna) de entradas para la función inversa.

Ejemplo\(\PageIndex{5}\): Interpreting the Inverse of a Tabular Function

\(f(t)\)Se da una función en la Tabla\(\PageIndex{3}\), mostrando la distancia en millas que un automóvil ha recorrido en\(t\) minutos. Buscar e interpretar\(f^{-1}(70)\)

Mesa\(\PageIndex{3}\)

\(t\)(minutos)	30	50	70	90
\(f(t)\)(millas)	20	40	60	70

La función inversa toma una salida de\(f\) y devuelve una entrada para\(f\). Entonces en la expresión\(f^{-1}(70)\), 70 es un valor de salida de la función original, que representa 70 millas. El inverso devolverá la entrada correspondiente de la función original\(f\), 90 minutos, así\(f^{-1}(70)=90\). La interpretación de esto es que, para conducir 70 millas, tardó 90 minutos.

Alternativamente, recordemos que la definición de lo inverso era que si\(f(a)=b\), entonces\(f^{-1}(b)=a\). Por esta definición, si nos dan\(f^{-1}(70)=a\), entonces estamos buscando un valor para\(a\) que eso\(f(a)=70\). En este caso, estamos buscando un\(t\) así que\(f(t)=70\), que es cuando\(t=90\).

Ejercicio\(\PageIndex{5}\)

Usando Table\(\PageIndex{4}\), encuentra e interpreta (a)\(f(60)\) y (b)\(f^{-1}(60)\).

Mesa\(\PageIndex{4}\)

\(t\)(minutos)	30	50	60	70	90
\(f(t)\)(millas)	20	40	50	60	70

Contestar

\(f(60)=50\). En 60 minutos, se recorren 50 millas.
\(f^{-1}(60)=70\). Para recorrer 60 millas, tardará 70 minutos.

Evaluación de la inversa de una función, dada una gráfica de la función original

Vimos en Funciones y Notación de Funciones que el dominio de una función puede leerse observando la extensión horizontal de su gráfica. Encontramos el dominio de la función inversa observando la extensión vertical de la gráfica de la función original, porque ésta corresponde a la extensión horizontal de la función inversa. De igual manera, encontramos el rango de la función inversa observando la extensión horizontal de la gráfica de la función original, ya que esta es la extensión vertical de la función inversa. Si queremos evaluar una función inversa, encontramos su entrada dentro de su dominio, que es todo o parte del eje vertical de la gráfica de la función original.

Dada la gráfica de una función, evaluar su inversa en puntos específicos.

1. Encuentre la entrada deseada en el eje y de la gráfica dada.
2. Lea la salida de la función inversa del eje x de la gráfica dada.

Ejemplo\(\PageIndex{6}\): Evaluating a Function and Its Inverse from a Graph at Specific Points

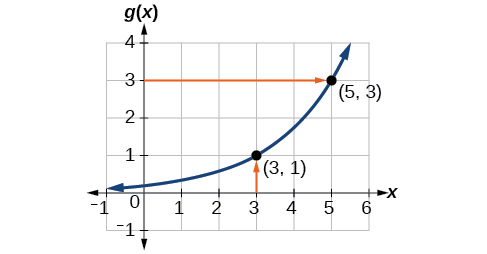
Una función\(g(x)\) se da en la Figura\(\PageIndex{5}\). Encontrar\(g(3)\) y\(g^{-1}(3)\).
.

\ (g (x)\)” src=” https://math.libretexts.org/@api/dek..._01_07_006.jpg "fileid="1023" />

Figura\(\PageIndex{5}\): Gráfica de\(g(x)\)

Solución

Para evaluar\(g(3)\), encontramos 3 en el eje x y encontramos el valor de salida correspondiente en el eje y. Eso nos\((3,1)\) dice el punto\(g(3)=1\).

Para evaluar\(g^{-1}(3)\), recordar que por definición\(g^{-1}(3)\) significa el valor de\(x\) para el cual\(g(x)=3\). Al buscar el valor de salida 3 en el eje vertical, encontramos el punto\((5,3)\) en la gráfica, lo que significa\(g(5)=3\), así que por definición,\(g^{-1}(3)=5.\) Ver Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Gráfica de\(g(x)\).

Ejercicio\(\PageIndex{6}\)

Usando la gráfica de la Figura\(\PageIndex{6}\), (a) encontrar\(g^{-1}(1)\), y (b) estimar\(g^{-1}(4)\).

Contestar a

3

Respuesta b

5.6

Búsqueda de inversos de funciones representadas por fórmulas

A veces necesitaremos conocer una función inversa para todos los elementos de su dominio, no solo para algunos. Si la función original se da como una fórmula —por ejemplo,\(y\) como una función de\(x\) — a menudo podemos encontrar la función inversa resolviendo para obtener\(x\) como una función de\(y\).

Cómo: Dada una función representada por una fórmula, encontrar la inversa.

1. Asegúrese de que\(f\) es una función uno a uno.
2. Resolver para\(x\)
3. Intercambio\(x\) y\(y\).

Ejemplo\(\PageIndex{7}\): Inverting the Fahrenheit-to-Celsius Function

Encuentra una fórmula para la función inversa que da temperatura Fahrenheit en función de la temperatura Celsius.

\[C=\dfrac{5}{9}(F−32)\]

Solución

\[\begin{align} C&=\frac{5}{9}(F-32) \\ C{\cdot}\frac{9}{5}&=F−32 \\ F&=\frac{9}{5}C+32\end{align}\]

Al resolver en general, hemos descubierto la función inversa. Si

\[C=h(F)=\dfrac{5}{9}(F−32)\],

entonces

\[F=h^{-1}(C)=\dfrac{9}{5}C+32.\]

En este caso, introdujimos una función\(h\) para representar la conversión porque las variables de entrada y salida son descriptivas, y la escritura\(C^{-1}\) podría resultar confusa.

Ejercicio\(\PageIndex{7}\)

Resolver para\(x\) en términos de\(y\) dado\(y=\frac{1}{3}(x−5)\)

Contestar

\(x=3y+5\)

Ejemplo\(\PageIndex{8}\): Solving to Find an Inverse Function

Encuentra la inversa de la función\(f(x)=\frac{2}{x−3}+4\).

Solución

\[\begin{align} y&=\dfrac{2}{x−3+4} &\text{Set up an equation.} \\ y−4&=\dfrac{2}{x−3} &\text{Subtract 4 from both sides.} \\ x−3&=\dfrac{2}{y−4} &\text{Multiply both sides by x−3 and divide by y−4.} \\ x&=\dfrac{2}{y−4}+3 &\text{Add 3 to both sides.} \end{align}\]

Entonces\(f^{-1}(y)=\frac{2}{y−4}+3\) o\(f^{-1}(x)=\frac{2}{x−4}+3\).

Análisis

El dominio y rango de\(f\) excluyen los valores 3 y 4, respectivamente. \(f\)y\(f^{-1}\) son iguales en dos puntos pero no son la misma función, como podemos ver al crear Tabla\(\PageIndex{5}\).

Mesa\(\PageIndex{5}\)

\(x\)	1	2	5	\(f^{-1}(y)\)
\(f(x)\)	3	2	5	\(y\)

Ejemplo\(\PageIndex{9}\): Solving to Find an Inverse with Radicals

Encuentra la inversa de la función\(f(x)=2+\sqrt{x−4}\).

Solución

\[ \begin{align} y&=2+\sqrt{x-4} \\ (y-2)^2&=x-4 \\ x&=(y-2)^2+4 \end{align}\]

Entonces\(f^{-1}(x)=(x−2)^2+4\).

El dominio de\(f\) es\(\left[4,\infty\right)\). Observe que el rango de\(f\) es\(\left[2,\infty\right)\), por lo que esto significa que el dominio de la función inversa también\(f^{-1}\) es\(\left[2,\infty\right)\)

Análisis

La fórmula que encontramos para\(f^{-1}(x)\) parece que sería válida para todos los reales\(x\). Sin embargo,\(f^{-1}\) en sí mismo debe tener una inversa (es decir,\(f\)) así que tenemos que restringir el dominio\(\left[2,\infty\right)\) de\(f^{-1}\) a para poder hacer\(f^{-1}\) una función uno a uno. Este dominio de\(f^{-1}\) es exactamente el rango de\(f\).

Ejercicio\(\PageIndex{8}\)

¿Cuál es la inversa de la función\(f(x)=2-\sqrt{x}\)? Declarar los dominios tanto de la función como de la función inversa.

Contestar

\(f^{-1}(x)=(2−x)^2\); dominio de\(f\):\(\left[0,\infty\right)\); dominio de\(f^{-1}\):\(\left(−\infty,2\right]\)

Encontrar funciones inversas y sus gráficas

Ahora que podemos encontrar la inversa de una función, exploraremos las gráficas de funciones y sus inversos. Volvamos a la función cuadrática\(f(x)=x^2\) restringida al dominio\(\left[0,\infty\right)\), en el que esta función es uno-a-uno, y graficarla como en la Figura\(\PageIndex{7}\).

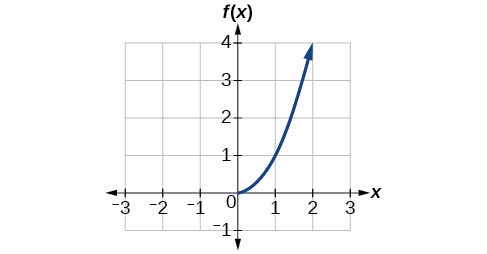
Figura\(\PageIndex{7}\): Función cuadrática con dominio restringido a\([0, \infty)\).

Restringir el dominio a\(\left[0,\infty\right)\) hace que la función sea uno a uno (obviamente pasará la prueba de línea horizontal), por lo que tiene una inversa en este dominio restringido.

Ya sabemos que la inversa de la función cuadrática del kit de herramientas es la función raíz cuadrada, es decir,\(f^{-1}(x)=\sqrt{x}\). ¿Qué sucede si graficamos ambos\(f\) y\(f^{-1}\) en el mismo conjunto de ejes, usando el eje x para la entrada a ambos\(f\) y\(f^{-1}\)?

Notamos una relación distinta: La gráfica de\(f^{-1}(x)\) es la gráfica de\(f(x)\) reflejada sobre la línea diagonal\(y=x\), a la que llamaremos la línea de identidad, mostrada en la Figura\(\PageIndex{8}\).

\ (f (x)\) y\(f^(-1)(x)\). "src=” https://math.libretexts.org/@api/dek..._01_07_009.jpg "fileid="1026" />.
Figura\(\PageIndex{8}\): Funciones de raíz cuadrada y cuadrada en el dominio no negativo

Esta relación se observará para todas las funciones uno a uno, ya que es resultado de la función y sus entradas y salidas de intercambio inverso. Esto equivale a intercambiar los roles de los ejes vertical y horizontal.

Ejemplo\(\PageIndex{10}\): Finding the Inverse of a Function Using Reflection about the Identity Line

Dada la gráfica de\(f(x)\) en la Figura\(\PageIndex{9}\), bosquejar una gráfica de\(f^{-1}(x)\).

\ (f^ (-1) (x)\)” src=” https://math.libretexts.org/@api/dek..._01_07_010.jpg "fileid="1027" />

Figura\(\PageIndex{9}\): Gráfica de\(f^(-1)(x)\).

Esta es una función uno a uno, por lo que podremos esbozar una inversa. Tenga en cuenta que la gráfica mostrada tiene un dominio aparente de\((0,\infty)\) y rango de\((−\infty,\infty)\), por lo que la inversa tendrá un dominio de\((−\infty,\infty)\) y rango de\((0,\infty)\).

Si reflejamos esta gráfica sobre la línea\(y=x\), el punto\((1,0)\) refleja hacia\((0,1)\) y el punto\((4,2)\) refleja hacia\((2,4)\). Croquizar la inversa en los mismos ejes que la gráfica original da Figura\(\PageIndex{10}\).

\ (f (x)\) y\(f^(-1)(x)\).” src=” https://math.libretexts.org/@api/dek..._01_07_011.jpg "fileid="1028" />

Figura\(\PageIndex{10}\): La función y su inversa, mostrando reflexión sobre la línea de identidad

Ejercicio\(\PageIndex{1}\)

Dibujar gráficas de las funciones\(f\) y\(f^{-1}\) de Ejemplo\(\PageIndex{8}\).

Contestar

\ (f (x)\) y\(f^(-1)(x)\).” src=” https://math.libretexts.org/@api/dek..._01_07_012.jpg "fileid="1029" />

Figura\(\PageIndex{11}\): Gráfica de\(f(x)\) y\(f^(-1)(x)\).

¿Hay alguna función que sea igual a su propia inversa?

Sí. Si\(f=f^{-1}\), entonces\(f(f(x))=x\), y podemos pensar en varias funciones que tienen esta propiedad. La función de identidad

lo hace, y también lo hace la función recíproca, porque

\[\dfrac{1}{\frac{1}{x}}=x\]

Cualquier función\(f(x)=c−x\), donde\(c\) es una constante, también es igual a su propia inversa.

Conceptos clave

• Si\(g(x)\) es la inversa de\(f(x)\), entonces\(g(f(x))=f(g(x))=x\).
• Cada una de las funciones del kit de herramientas tiene una inversa.
• Para que una función tenga un inverso, debe ser uno a uno (pasar la prueba de línea horizontal).
• Una función que no sea uno a uno en todo su dominio puede ser uno a uno en parte de su dominio.
• Para una función tabular, intercambie las filas de entrada y salida para obtener la inversa.
• La inversa de una función se puede determinar en puntos específicos de su gráfica.
• Para encontrar la inversa de una fórmula, resolver la ecuación\(y=f(x)\) para\(x\) como una función de\(y\). Después intercambia las etiquetas\(x\) y\(y\).
• La gráfica de una función inversa es el reflejo de la gráfica de la función original a través de la línea\(y=x\).