4.3: Modelado con Funciones Lineales

Objetivos de aprendizaje

• Construir modelos lineales a partir de descripciones verbales.
• Modele un conjunto de datos con una función lineal.

Emily es una estudiante universitaria que planea pasar un verano en Seattle. Ella ha ahorrado $3,500 para su viaje y anticipa gastar 400 dólares cada semana en renta, comida y actividades. ¿Cómo podemos escribir un modelo lineal para representar su situación? ¿Cuál sería la intercepción x y qué puede aprender de ella? Para responder a estas y otras preguntas relacionadas, podemos crear un modelo utilizando una función lineal. Modelos como este pueden ser extremadamente útiles para analizar relaciones y hacer predicciones basadas en esas relaciones. En esta sección, exploraremos ejemplos de modelos de funciones lineales.

Figura\(\PageIndex{1}\): (crédito: EEK Photography/Flickr)

Identificar pasos para modelar y resolver problemas

Al modelar escenarios con funciones lineales y resolver problemas que involucran cantidades con una tasa de cambio constante, normalmente seguimos las mismas estrategias de problemas que usaríamos para cualquier tipo de función. Vamos a revisarlos brevemente:

Identifique las cantidades cambiantes y, a continuación, defina variables descriptivas para representar esas cantidades. Cuando sea apropiado, esboce una imagen o defina un sistema de coordenadas.
Lea atentamente el problema para identificar información importante. Busque información que proporcione valores para las variables o valores para partes del modelo funcional, como pendiente y valor inicial.
Lea atentamente el problema para determinar lo que estamos tratando de encontrar, identificar, resolver o interpretar.
Identificar una vía de solución desde la información proporcionada hasta lo que estamos tratando de encontrar. A menudo esto implicará verificar y rastrear unidades, construir una mesa o incluso encontrar una fórmula para la función que se usa para modelar el problema.
Cuando sea necesario, escriba una fórmula para la función.
Resolver o evaluar la función usando la fórmula.
Reflexiona sobre si tu respuesta es razonable para la situación dada y si tiene sentido matemáticamente.
Transmite claramente tu resultado usando las unidades apropiadas, y responde en oraciones completas cuando sea necesario.

Construcción de Modelos Lineales

Ahora echemos un vistazo al estudiante en Seattle. En su situación, hay dos cantidades cambiantes: el tiempo y el dinero. La cantidad de dinero que le queda mientras está de vacaciones depende de cuánto tiempo se quede. Podemos usar esta información para definir nuestras variables, incluyendo unidades.

• Salida:\(M\), dinero restante, en dólares
• Entrada:\(t\), tiempo, en semanas

Entonces, la cantidad de dinero restante depende del número de semanas:\(M(t)\)

También podemos identificar el valor inicial y la tasa de cambio.

• Valor Inicial: Ella ahorró $3,500, por lo que $3,500 es el valor inicial para M.
• Tasa de Cambio: Ella anticipa gastar $400 cada semana, por lo que —$400 por semana es la tasa de cambio, o pendiente.

Observe que la unidad de dólares por semana coincide con la unidad de nuestra variable de salida dividida por nuestra variable de entrada. Además, debido a que la pendiente es negativa, la función lineal es decreciente. Esto debería tener sentido porque ella está gastando dinero cada semana.

La tasa de cambio es constante, por lo que podemos comenzar con el modelo lineal\(M(t)=mt+b\). Entonces podemos sustituir la intercepción y pendiente proporcionada.

Figura\(\PageIndex{2}\)

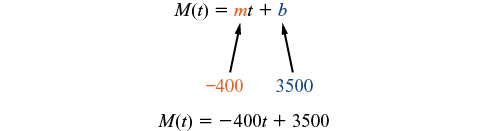
Para encontrar la intercepción x, establecemos la salida en cero y resolvemos la entrada.

\[\begin{align*} 0&=−400t+3500 \\ t&=\dfrac{3500}{400} \\ &=8.75 \end{align*}\]

La intercepción x es de 8.75 semanas. Debido a que esto representa el valor de entrada cuando la salida será cero, podríamos decir que a Emily no le quedará dinero después de 8.75 semanas.

Al modelar cualquier escenario de la vida real con funciones, normalmente hay un dominio limitado sobre el cual ese modelo será válido, casi ninguna tendencia continúa indefinidamente. Aquí el dominio se refiere al número de semanas. En este caso, no tiene sentido hablar de valores de entrada menores a cero. Un valor de entrada negativo podría referirse a varias semanas antes de que ella ahorrara $3,500, pero el escenario discutido plantea la pregunta una vez que ella ahorró $3,500 porque es entonces cuando comienza su viaje y posterior gasto. También es probable que este modelo no sea válido después de la intercepción x, a menos que Emily use una tarjeta de crédito y entre en deuda. El dominio representa el conjunto de valores de entrada, por lo que el dominio razonable para esta función es\(0{\leq}t{\leq}8.75\).

En el ejemplo anterior, se nos dio una descripción escrita de la situación. Seguimos los pasos de modelar un problema para analizar la información. No obstante, la información proporcionada puede no ser siempre la misma. A veces se nos puede proporcionar una intercepción. Otras veces se nos podría proporcionar un valor de salida. Debemos tener cuidado de analizar la información que se nos da, y utilizarla adecuadamente para construir un modelo lineal.

Uso de una Intercepción Dada para Construir un Modelo

Algunos problemas del mundo real proporcionan la intersección y, que es el valor constante o inicial. Una vez que se conoce la intersección y, se puede calcular la intercepción x. Supongamos, por ejemplo, que Hannah planea pagar un préstamo sin intereses de sus padres. El saldo de su préstamo es de $1,000. Ella planea pagar $250 mensuales hasta que su saldo sea de $0. La intersección y es el monto inicial de su deuda, o $1,000. La tasa de cambio, o pendiente, es de -$250 mensuales. Luego podemos usar la forma pendiente-intercepción y la información dada para desarrollar un modelo lineal.

\[\begin{align*} f(x)&=mx+b \\ &=-250x+1000 \end{align*}\]

Ahora podemos establecer la función igual a 0, y resolver\(x\) para encontrar la intercepción x.

\[\begin{align*} 0&=-250+1000 \\ 1000&=250x \\ 4&=x \\ x&=4 \end{align*}\]

El x-intercept es el número de meses que le lleva alcanzar un saldo de $0. El x-intercept es de 4 meses, por lo que Hannah tardará cuatro meses en pagar su préstamo.

Uso de una entrada y salida dadas para construir un modelo

Muchas aplicaciones del mundo real no son tan directas como las que acabamos de considerar. En cambio, requieren que identifiquemos algún aspecto de una función lineal. A veces se nos podría pedir que evaluemos el modelo lineal en una entrada dada o establecer la ecuación del modelo lineal igual a una salida especificada.

Ante un problema de palabras que incluye dos pares de valores de entrada y salida, utilice la función lineal para resolver un problema.

1. Identificar los valores de entrada y salida.
2. Convierta los datos en dos pares de coordenadas.
3. Encuentra la pendiente.
4. Escribe el modelo lineal.
5. Utilice el modelo para hacer una predicción evaluando la función en un valor x dado.
6. Utilice el modelo para identificar un valor x que resulte en un valor y dado.
7. Responde a la pregunta planteada.

Ejemplo\(\PageIndex{1}\): Using a Linear Model to Investigate a Town’s Population

La población de un pueblo ha ido creciendo linealmente. En 2004 la población era de 6.200 habitantes. Para 2009 la población había crecido a 8,100. Supongamos que esta tendencia continúa.

1. Predecir la población en 2013.
2. Identificar el año en que la población alcanzará los 15 mil.

Solución

Las dos cantidades cambiantes son el tamaño de la población y el tiempo. Si bien podríamos usar el valor real del año como la cantidad de entrada, hacerlo tiende a llevar a ecuaciones muy engorrosas porque la intersección y correspondería al año 0, ¡hace más de 2000 años!

Para que la computación sea un poco más agradable, definiremos nuestra entrada como el número de años desde 2004:

• Entrada:\(t\), años desde 2004
• Salida:\(P(t)\), la población del pueblo

Para predecir la población en 2013 (\(t=9\)), primero necesitaríamos una ecuación para la población. De igual manera, para encontrar cuándo llegaría la población a los 15 mil, necesitaríamos resolver para el insumo que proporcionaría una producción de 15 mil. Para escribir una ecuación, necesitamos el valor inicial y la tasa de cambio, o pendiente.

Para determinar la tasa de cambio, utilizaremos el cambio en la salida por cambio en la entrada.

\[m=\dfrac{\text{change in output}}{\text{change in input}}\]

El problema nos da dos pares entrada-salida. Convirtiéndolos para que coincidan con nuestras variables definidas, correspondería al año 2004\(t=0\), dando el punto\((0,6200)\). Observe que a través de nuestra inteligente elección de definición de variable, nos hemos “dado” a nosotros mismos la intersección y de la función. El año 2009 correspondería\(t=5\), dando el punto\((5,8100)\).

Los dos pares de coordenadas son\((0,6200)\) y\((5,8100)\). Recordemos que nos encontramos con ejemplos en los que nos proporcionaron dos puntos antes en el capítulo. Podemos usar estos valores para calcular la pendiente.

\[\begin{align*} m&=\dfrac{8100-6200}{5-0}\\ &=\dfrac{1900}{5} \\ &=380 \text{ people per year} \end{align*}\]

Ya conocemos la intersección y de la línea, por lo que podemos escribir inmediatamente la ecuación:

\[P(t)=380t+6200\]

Para predecir la población en 2013, evaluamos nuestra función en\(t=9\).

\[\begin{align*} P(9)&=380(9)+6,200 \\ &=9,620 \end{align*}\]

Si la tendencia continúa, nuestro modelo predice una población de 9.620 habitantes en 2013.

Para saber cuándo llegará la población a los 15 mil, podemos establecer\(P(t)=15000\) y resolver para\(t\).

\[\begin{align*} 15000&=380t+6200 \\ 8800&=380t \\ t&{\approx}23.158 \end{align*}\]

Nuestro modelo predice que la población alcanzará los 15,000 en poco más de 23 años después de 2004, o en algún lugar alrededor del año 2027.

Ejercicio\(\PageIndex{1A}\)

Una empresa vende donas. Incurren un costo fijo de $25,000 por renta, seguro y otros gastos. Cuesta $0.25 producir cada donut.

1. Escribir un modelo lineal para representar el costo C de la empresa en función de\(x\), el número de donas producidas.
2. Encuentra e interpreta la intersección y.

Solución

a.\(C(x)=0.25x+25,000\) b. La intercepción y es\((0,25,000)\). Si la compañía no produce un solo donut, aún incurren en un costo de $25,000.

Ejercicio\(\PageIndex{1B}\)

La población de una ciudad ha ido creciendo linealmente. En 2008, la población era de 28.200 habitantes. Para 2012, la población era de 36 mil 800. Supongamos que esta tendencia continúa.

1. Predecir la población en 2014.
2. Identificar el año en que la población llegará a 54 mil.

Solución

a. 41,100 b. 2020

Uso de un diagrama para modelar un problema

Es útil para muchas aplicaciones del mundo real dibujar una imagen para tener una idea de cómo las variables que representan la entrada y la salida pueden usarse para responder una pregunta. Para dibujar el cuadro, primero considere cuál es lo que pide el problema. Después, determine la entrada y la salida. El diagrama debe relacionar las variables. A menudo, se dibujan formas geométricas o figuras. A menudo se trazan distancias. Si se esboza un triángulo rectángulo, el Teorema de Pitágoras relaciona los lados. Si se esboza un rectángulo, es útil etiquetar ancho y alto.

Ejemplo\(\PageIndex{2}\): Using a Diagram to Model Distance Walked

Anna y Emanuel parten en la misma intersección. Anna camina hacia el este a 4 millas por hora mientras Emanuel camina hacia el sur a 3 millas por hora. Se están comunicando con una radio bidireccional que tiene un alcance de 2 millas. ¿Cuánto tiempo después de que comiencen a caminar se caerán fuera del contacto por radio?

Solución

En esencia, podemos responder parcialmente a esta pregunta diciendo que se quedarán fuera del contacto por radio cuando estén a 2 millas de distancia, lo que nos lleva a hacer una nueva pregunta:

“¿Cuánto tiempo les llevará estar a 2 millas de distancia?”

En este problema, nuestras cantidades cambiantes son tiempo y posición, pero en última instancia necesitamos saber cuánto tiempo les llevará estar a 2 millas de distancia. Podemos ver que el tiempo será nuestra variable de entrada, así vamos a definir nuestras variables de entrada y salida.

• Entrada:\(t\), tiempo en horas.
• Salida:\(A(t)\), distancia en millas y\(E(t)\), distancia en millas

Debido a que no es obvio cómo definir nuestra variable de salida, comenzaremos dibujando una imagen como Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\)

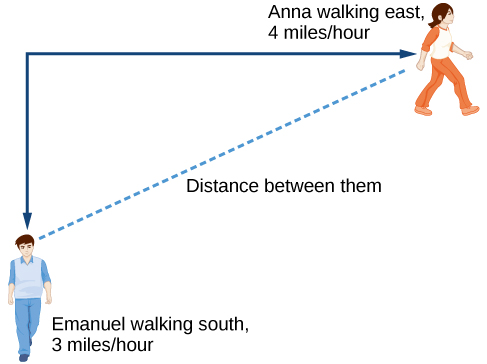
• Valor Inicial: Ambos inician en la misma intersección por lo que cuando\(t=0\), la distancia recorrida por cada persona también debe ser 0. Por lo tanto, el valor inicial para cada uno es 0.
• Tasa de Cambio: Anna está caminando 4 millas por hora y Emanuel está caminando 3 millas por hora, que son ambas tasas de cambio. La pendiente para\(A\) es 4 y la pendiente para\(E\) es 3.

Usando esos valores, podemos escribir fórmulas para la distancia que ha caminado cada persona.

\[A(t)=4t\]

\[E(t)=3t\]

Para este problema, las distancias desde el punto de partida son importantes. Para anotar estos, podemos definir un sistema de coordenadas, identificando el “punto de partida” en la intersección donde ambos comenzaron. Entonces podemos usar la variable\(A\), que introdujimos anteriormente, para representar la posición de Anna, y definirla como una medida desde el punto de partida en dirección este. Asimismo, se puede utilizar la variable\(E\),, para representar la posición de Emanuel, medida desde el punto de partida en dirección sur. Tenga en cuenta que al definir el sistema de coordenadas, especificamos tanto el punto de inicio de la medición como la dirección de la medida.

Entonces podemos definir una tercera variable,\(D\), para ser la medida de la distancia entre Anna y Emanuel. Mostrar las variables en el diagrama suele ser útil, como podemos ver en la Figura\(\PageIndex{4}\).

Recordemos que necesitamos saber cuánto tiempo lleva\(D\), la distancia entre ellos, para igualar 2 millas. Observe que para cualquier entrada dada\(t\), las salidas\(A(t)\)\(E(t)\), y\(D(t)\) representan distancias.

Figura\(\PageIndex{4}\): Podemos usar el Teorema de Pitágoras porque hemos dibujado un ángulo recto.

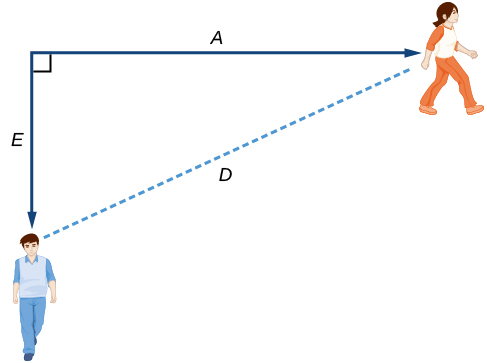
Usando el Teorema de Pitágoras, obtenemos:

\[\begin{align*} d(t)^2&=A(t)^2+E(t)^2 \\ &=(4t)^2+(3t)^2 \\ &=16t^2+9t^2 \\ &=25t^2 \\ D(t)&=\pm\sqrt{25t^2} &\text{Solve for $D(t)$ using the square root} \\ &= \pm 5|t| \end{align*}\]

En este escenario estamos considerando sólo valores positivos de\(t\), por lo que nuestra distancia siempre\(D(t)\) será positiva. Podemos simplificar esta respuesta a\(D(t)=5t\). Esto quiere decir que la distancia entre Anna y Emanuel es también una función lineal. Debido a que D es una función lineal, ahora podemos responder a la pregunta de cuándo la distancia entre ellos alcanzará 2 millas. Estableceremos la salida\(D(t)=2\) y resolveremos para\(t\).

\[\begin{align*} D(t)&=2 \\ 5t&=2 \\ t&=\dfrac{2}{5}=0.4 \end{align*}\]

Se caerán del contacto por radio en 0.4 horas, o 24 minutos.

¿Debo dibujar diagramas cuando se le da información basada en una forma geométrica?

Sí. Dibuje la figura y etiquete las cantidades e incógnitas en el boceto.

Ejemplo\(\PageIndex{3}\): Using a Diagram to Model Distance between Cities

Hay una carretera recta que va de la ciudad de Westborough a Agritown 30 millas al este y 10 millas al norte. A mitad de esta carretera, se une con una segunda carretera, perpendicular a la primera, que conduce a la ciudad de Eastborough. Si la ciudad de Eastborough se encuentra a 20 millas directamente al este de la ciudad de Westborough, ¿a qué distancia está el cruce de carreteras de Westborough?

Solución

Podría ayudar aquí para hacer una imagen de la situación. Ver Figura\(\PageIndex{5}\). Entonces sería útil introducir un sistema de coordenadas. Si bien podríamos colocar el origen en cualquier lugar, colocarlo en Westborough parece conveniente. Esto pone a Agritown en las coordenadas\((30, 10)\), y Eastborough en\((20,0)\).

Figura\(\PageIndex{5}\)

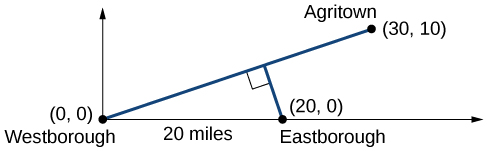
Usando este punto junto con el origen, podemos encontrar la pendiente de la línea de Westborough a Agritown:

\[m=\dfrac{10-0}{30-0}=\dfrac{1}{3}\]

La ecuación de la carretera de Westborough a Agritown sería

\[W(x)=\dfrac{1}{3}x\]

A partir de esto, podemos determinar la carretera perpendicular a Eastborough que tendrá pendiente\(m=–3\). Debido a que el pueblo de Eastborough está en ese punto\((20, 0)\), podemos encontrar la ecuación:

\[\begin{align*} E(x)&=−3x+b \\ 0&=−3(20)+b &\text{Substitute in $(20, 0)$} \\ b&=60 \\ E(x)&=−3x+60 \end{align*}\]

Ahora podemos encontrar las coordenadas del cruce de las carreteras al encontrar la intersección de estas líneas. Estableciéndolos iguales,

\[\begin{align*} \dfrac{1}{3}x&=−3x+60 \\ \dfrac{10}{3}x&=60 \\ 10x&=180 \\ x&=18 &\text{Substituting this back into $W(x)$} \\ y&=W(18) \\ &= \dfrac{1}{3}(18) \\&=6 \end{align*}\]

Los caminos se cruzan en el punto\((18,6)\). Usando la fórmula de distancia, ahora podemos encontrar la distancia desde Westborough hasta el cruce.

\[\begin{align*} \text{distance}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ &=\sqrt{(18-0)^2+(6-0)^2} \\ &\approx 18.743 \text{miles} \end{align*}\]

Análisis

Un buen uso de los modelos lineales es aprovechar el hecho de que las gráficas de estas funciones son líneas. Esto significa que las aplicaciones del mundo real que discuten mapas necesitan funciones lineales para modelar las distancias entre los puntos de referencia.

Ejercicio\(\PageIndex{2}\)

Hay una carretera recta que va desde la ciudad de Timpson hasta Ashburn 60 millas al este y 12 millas al norte. A parte del camino, se une con una segunda carretera, perpendicular a la primera, que conduce a la localidad de Garrison. Si el pueblo de Garrison se encuentra a 22 millas directamente al este de la ciudad de Timpson, ¿a qué distancia está el cruce vial de Timpson?

Solución

21.15 millas

Sistemas de Construcción de Modelos Lineales

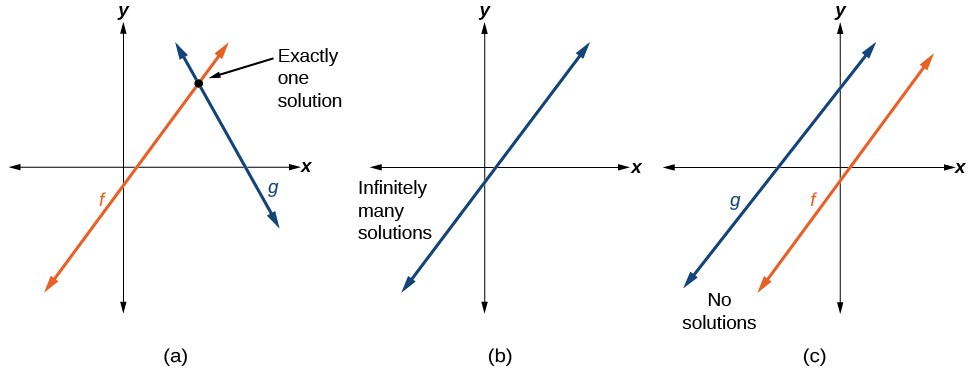
Las situaciones del mundo real que incluyen dos o más funciones lineales pueden modelarse con un sistema de ecuaciones lineales. Recuerde, al resolver un sistema de ecuaciones lineales, estamos buscando puntos que las dos líneas tengan en común. Por lo general, existen tres tipos de respuestas posibles, como se muestra en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)

Ante una situación que representa un sistema de ecuaciones lineales, escribir el sistema de ecuaciones e identificar la solución.

1. Identificar la entrada y salida de cada modelo lineal.
2. Identificar la pendiente y la intersección en y de cada modelo lineal.
3. Encuentre la solución estableciendo las dos funciones lineales iguales a otra y resolviendo para\(x\), o encontrar el punto de intersección en una gráfica.

Ejemplo\(\PageIndex{4}\): Building a System of Linear Models to Choose a Truck Rental Company

Jamal elige entre dos empresas de alquiler de camiones. El primero, Keep on Trucking, Inc., cobra una tarifa inicial de $20, luego 59 centavos la milla [1]. El segundo, Move It Your Way, cobra una tarifa inicial de 16 dólares, luego 63 centavos la milla. ¿Cuándo será Keep on Trucking, Inc. la mejor opción para Jamal?

Solución

Las dos cantidades importantes en este problema son el costo y el número de millas recorridas. Debido a que tenemos dos empresas a considerar, vamos a definir dos funciones.

• Entrada:\(d\), distancia recorrida en millas
• Salidas:\(K(d):\) costo, en dólares, para rentar de Keep on Trucking

\(M(d):\)costo, en dólares, para rentar de Move It Your Way

• Valor inicial: Tarifa inicial:\(K(0)=20\) y\(M(0)=16\)
• Tasa de cambio:\(K(d)=\dfrac{$0.59}{\text{mile}}\) y\(P(d)=\dfrac{$0.63}{\text{mile}}\)

Una función lineal es de la forma\(f(x)=mx+b\). Usando las tasas de cambio y las cargas iniciales, podemos escribir las ecuaciones

\[K(d)=0.59d+20 \nonumber\]

\[M(d)=0.63d+16 \nonumber\]

Usando estas ecuaciones, podemos determinar cuándo Keep on Trucking, Inc. será la mejor opción. Porque todo lo que tenemos que tomar esa decisión son los costos, estamos buscando cuando Keep on Trucking, Inc. costará menos, o cuando\(K(d)<M(d)\). El camino de solución nos llevará a encontrar las ecuaciones para las dos funciones, encontrar la intersección y luego ver dónde la\(K(d)\) función es más pequeña.

Estas gráficas se esbozan en Figura\(\PageIndex{7}\), con\(K(d)\) en azul.

Figura\(\PageIndex{7}\)

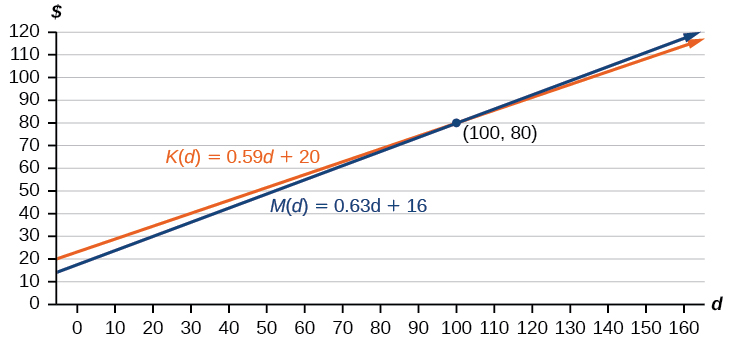
Para encontrar la intersección, establecemos las ecuaciones iguales y resolvemos:

\[\begin{align*} K(d)&=M(d) \\ 0.59d+20&=0.63d+16 \\ 4&=0.04d \\ 100&=d \\ d&=100 \end{align*}\]

Esto nos dice que el costo de las dos empresas será el mismo si se recorren 100 millas. Ya sea mirando la gráfica, o señalando que\(K(d)\) está creciendo a un ritmo más lento, podemos concluir que Keep on Trucking, Inc. será el precio más barato cuando se conduzcan más de 100 millas, es decir\(d>100\).

Conceptos clave

• Podemos usar las mismas estrategias de problema que usaríamos para cualquier tipo de función.
• Al modelar y resolver un problema, identifique las variables y busque valores clave, incluyendo la pendiente y la intersección en y.
• Dibuje un diagrama, en su caso.
• Verifique la razonabilidad de la respuesta.
• Los modelos lineales se pueden construir identificando o calculando la pendiente y usando la intersección y.
• La intercepción x se puede encontrar configurando\(y=0\), que es establecer la expresión\(mx+b\) igual a 0.
• El punto de intersección de un sistema de ecuaciones lineales es el punto donde los valores x e y son los mismos.
• Se puede utilizar una gráfica del sistema para identificar los puntos donde una línea cae por debajo (o por encima) de la otra línea.

Notas al pie

1 Tarifas recuperadas Ago 2, 2010 de www.budgettruck.com y http://www.uhaul.com/