7.2: Sistemas de Ecuaciones Lineales - Dos Variables
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Resolver sistemas de ecuaciones mediante la gráfica.
- Resolver sistemas de ecuaciones por sustitución.
- Resolver sistemas de ecuaciones por suma.
- Identificar sistemas inconsistentes de ecuaciones que contengan dos variables.
- Expresar la solución de un sistema de ecuaciones dependientes que contenga dos variables.
Un fabricante de monopatines presenta una nueva línea de tablas. El fabricante rastrea sus costos, que es la cantidad que gasta para producir los tableros, y sus ingresos, que es la cantidad que gana a través de las ventas de sus tableros. ¿Cómo puede determinar la compañía si está obteniendo ganancias con su nueva línea? ¿Cuántas patinetas deben producirse y venderse antes de que sea posible obtener ganancias? En esta sección, consideraremos ecuaciones lineales con dos variables para responder a estas y similares preguntas.

Introducción a los Sistemas de Ecuaciones
Para investigar situaciones como la del fabricante de monopatines, necesitamos reconocer que estamos tratando con más de una variable y probablemente más de una ecuación. Un sistema de ecuaciones lineales consiste en dos o más ecuaciones lineales compuestas por dos o más variables de manera que todas las ecuaciones del sistema se consideran simultáneamente. Para encontrar la solución única a un sistema de ecuaciones lineales, debemos encontrar un valor numérico para cada variable en el sistema que satisfaga todas las ecuaciones del sistema al mismo tiempo. Algunos sistemas lineales pueden no tener una solución y otros pueden tener un número infinito de soluciones. Para que un sistema lineal tenga una solución única, debe haber al menos tantas ecuaciones como variables haya. Aun así, esto no garantiza una solución única.
En esta sección, veremos sistemas de ecuaciones lineales en dos variables, que consisten en dos ecuaciones que contienen dos variables diferentes. Por ejemplo, considere el siguiente sistema de ecuaciones lineales en dos variables.
2x+y=153x–y=5
La solución a un sistema de ecuaciones lineales en dos variables es cualquier par ordenado que satisfaga cada ecuación de forma independiente. En este ejemplo, el par ordenado(4,7) es la solución al sistema de ecuaciones lineales. Podemos verificar la solución sustituyendo los valores en cada ecuación para ver si el par ordenado satisface ambas ecuaciones. En breve investigaremos métodos para encontrar tal solución si existe.
2(4)+(7)=15 True3(4)−(7)=5 True
Además de considerar el número de ecuaciones y variables, podemos categorizar sistemas de ecuaciones lineales por el número de soluciones. Un sistema consistente de ecuaciones tiene al menos una solución. Un sistema consistente se considera un sistema independiente si tiene una única solución, como el ejemplo que acabamos de explorar. Las dos líneas tienen diferentes pendientes y se cruzan en un punto del plano. Un sistema consistente se considera un sistema dependiente si las ecuaciones tienen la misma pendiente y las mismas intercepciones y. En otras palabras, las líneas coinciden por lo que las ecuaciones representan la misma línea. Cada punto de la línea representa un par de coordenadas que satisface el sistema. Así, hay un número infinito de soluciones.
Otro tipo de sistema de ecuaciones lineales es un sistema inconsistente, que es aquel en el que las ecuaciones representan dos líneas paralelas. Las líneas tienen la misma pendiente y diferentes intercepciones y. No hay puntos comunes a ambas líneas; de ahí que no haya solución al sistema.
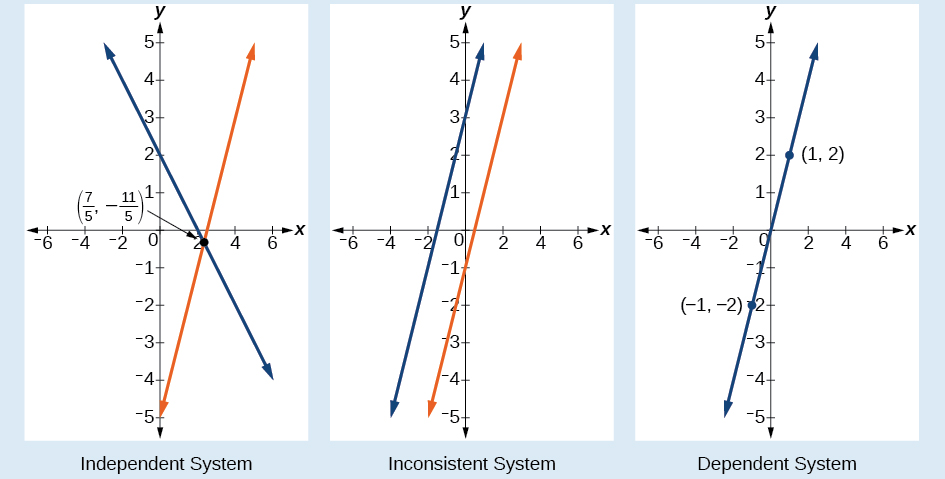
Existen tres tipos de sistemas de ecuaciones lineales en dos variables, y tres tipos de soluciones.
- Un sistema independiente tiene exactamente un par de soluciones(x,y). El punto donde se cruzan las dos líneas es la única solución.
- Un sistema inconsistente no tiene solución. Observe que las dos líneas son paralelas y nunca se cruzarán.
- Un sistema dependiente tiene infinitamente muchas soluciones. Las líneas son coincidentes. Son la misma línea, por lo que cada par de coordenadas en la línea es una solución a ambas ecuaciones.
La figura7.2.2 compara representaciones gráficas de cada tipo de sistema.
- Sustituir el par ordenado en cada ecuación en el sistema.
- Determinar si las declaraciones verdaderas resultan de la sustitución en ambas ecuaciones; si es así, el par ordenado es una solución.
Determinar si el par ordenado(5,1) es una solución al sistema de ecuaciones dado.
x+3y=82x−9=y
Solución
Sustituir el par ordenado(5,1) en ambas ecuaciones.
(5)+3(1)=88=8 True2(5)−9=(1)1=1 True
El par ordenado(5,1) satisface ambas ecuaciones, por lo que es la solución al sistema.
Análisis
Podemos ver la solución claramente trazando la gráfica de cada ecuación. Dado que la solución es un par ordenado que satisface ambas ecuaciones, es un punto en ambas líneas y por lo tanto el punto de intersección de las dos líneas. Ver Figura7.2.3.
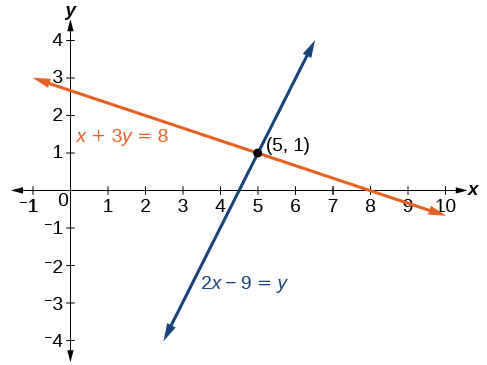
Determinar si el par ordenado(8,5) es una solución al siguiente sistema.
5x−4y=202x+1=3y
- Contestar
-
No es una solución.
Resolver Sistemas de Ecuaciones por Gráfica
Existen múltiples métodos para resolver sistemas de ecuaciones lineales. Para un sistema de ecuaciones lineales en dos variables, podemos determinar tanto el tipo de sistema como la solución graficando el sistema de ecuaciones en el mismo conjunto de ejes.
Resolver el siguiente sistema de ecuaciones graficando. Identificar el tipo de sistema.
2x+y=−8x−y=−1
Solución
Resuelve la primera ecuación paray.
2x+y=−8y=−2x−8
Resuelve la segunda ecuación paray.
x−y=−1y=x+1
Grafique ambas ecuaciones en el mismo conjunto de ejes que en la Figura7.2.4.
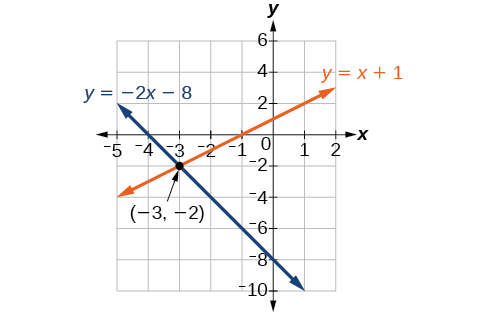
Las líneas parecen cruzarse en el punto(−3,−2). Podemos verificar para asegurarnos de que esta es la solución al sistema sustituyendo el par ordenado en ambas ecuaciones.
2(−3)+(−2)=−8−8=−8 True(−3)−(−2)=−1−1=−1 True
La solución al sistema es el par ordenado(−3,−2), por lo que el sistema es independiente.
Resolver el siguiente sistema de ecuaciones graficando.
2x−5y=−25−4x+5y=35
- Contestar
-
La solución al sistema es el par ordenado(−5,3).
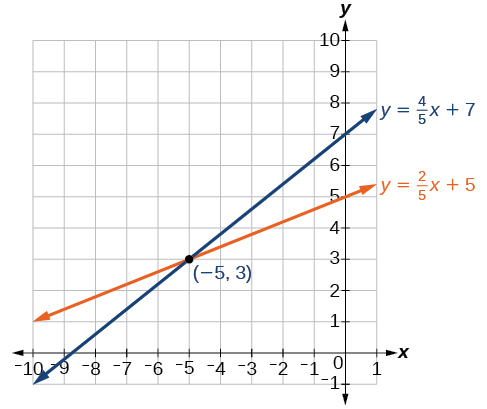
Figura7.2.5
¿Se puede utilizar la gráfica si el sistema es inconsistente o dependiente?
Sí, en ambos casos aún podemos graficar el sistema para determinar el tipo de sistema y solución. Si las dos líneas son paralelas, el sistema no tiene solución y es inconsistente. Si las dos líneas son idénticas, el sistema tiene infinitas soluciones y es un sistema dependiente.
Resolver Sistemas de Ecuaciones por Sustitución
Resolver un sistema lineal en dos variables mediante gráficos funciona bien cuando la solución consiste en valores enteros, pero si nuestra solución contiene decimales o fracciones, no es el método más preciso. Consideraremos dos métodos más para resolver un sistema de ecuaciones lineales que sean más precisos que la gráfica. Uno de esos métodos es resolver un sistema de ecuaciones por el método de sustitución, en el que resolvemos una de las ecuaciones para una variable y luego sustituimos el resultado por la segunda ecuación para resolver por la segunda variable. Recordemos que solo podemos resolver por una variable a la vez, que es la razón por la que el método de sustitución es valioso y práctico.
- Resolver una de las dos ecuaciones para una de las variables en términos de la otra.
- Sustituya la expresión de esta variable en la segunda ecuación, luego resuelva para la variable restante.
- Sustituya esa solución en cualquiera de las ecuaciones originales para encontrar el valor de la primera variable. Si es posible, escriba la solución como un par ordenado.
- Verifique la solución en ambas ecuaciones.
Resolver el siguiente sistema de ecuaciones por sustitución.
−x+y=−52x−5y=1
Solución
Primero, resolveremos la primera ecuación paray.
−x+y=−5y=x−5
Ahora podemos sustituir la expresiónx−5 pory en la segunda ecuación.
2x−5y=12x−5(x−5)=12x−5x+25=1−3x=−24x=8
Ahora, sustituimosx=8 en la primera ecuación y resolvemos paray.
−(8)+y=−5y=3
Nuestra solución es(8,3).
Verifique la solución sustituyéndola(8,3) en ambas ecuaciones.
−x+y=−5−(8)+(3)=−5 True2x−5y=12(8)−5(3)=1 True
Resolver el siguiente sistema de ecuaciones por sustitución.
x=y+34=3x−2y
- Contestar
-
(−2,−5)
¿Se puede utilizar el método de sustitución para resolver cualquier sistema lineal en dos variables?
Sí, pero el método funciona mejor si una de las ecuaciones contiene un coeficiente de1 o–1 así que no tenemos que tratar con fracciones.
Resolver Sistemas de Ecuaciones en Dos Variables por el Método de Adición
Un tercer método para resolver sistemas de ecuaciones lineales es el método de adición. En este método, sumamos dos términos con la misma variable, pero coeficientes opuestos, para que la suma sea cero. Por supuesto, no todos los sistemas se configuran con los dos términos de una variable que tiene coeficientes opuestos. Muchas veces debemos ajustar una o ambas ecuaciones por multiplicación para que una variable sea eliminada por suma.
- Escribe ambas ecuaciones con variables x - e y -en el lado izquierdo del signo igual y constantes a la derecha.
- Escribe una ecuación por encima de la otra, alineando las variables correspondientes. Si una de las variables de la ecuación superior tiene el coeficiente opuesto de la misma variable en la ecuación inferior, sumar las ecuaciones juntas, eliminando una variable. Si no, usa la multiplicación por un número distinto de cero para que una de las variables en la ecuación superior tenga el coeficiente opuesto de la misma variable en la ecuación inferior, luego agregue las ecuaciones para eliminar la variable.
- Resolver la ecuación resultante para la variable restante.
- Sustituir ese valor en una de las ecuaciones originales y resolver para la segunda variable.
- Verifique la solución sustituyendo los valores en la otra ecuación.
Resolver el sistema dado de ecuaciones por suma.
x+2y=−1−x+y=3
Solución
Ambas ecuaciones ya están establecidas iguales a una constante. Observe que el coeficiente dex en la segunda ecuación–1,, es lo opuesto al coeficiente dex en la primera ecuación,1. Podemos sumar las dos ecuaciones para eliminarx sin necesidad de multiplicar por una constante.
x+2y=−1−x+y_=3_3y=2
Ahora que hemos eliminadox, podemos resolver la ecuación resultante paray.
3y=2y=23
Entonces, sustituimos este valor pory en una de las ecuaciones originales y resolvemos parax.
−x+y=3−x+23=3−x=3−23−x=73x=−73
La solución a este sistema es(−73,23).
Verifique la solución en la primera ecuación.
x+2y=−1(−73)+2(23)=−73+43=−33−1=−1True
Análisis
Obtenemos una perspectiva importante sobre los sistemas de ecuaciones al observar la representación gráfica. Ver Figura7.2.6 para encontrar que las ecuaciones se cruzan en la solución. No necesitamos preguntar si puede haber una segunda solución porque observar la gráfica confirma que el sistema tiene exactamente una solución.
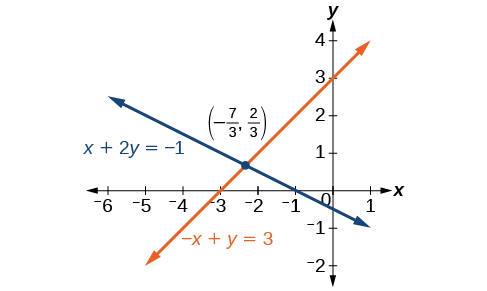
Resolver el sistema de ecuaciones dado por el método de suma.
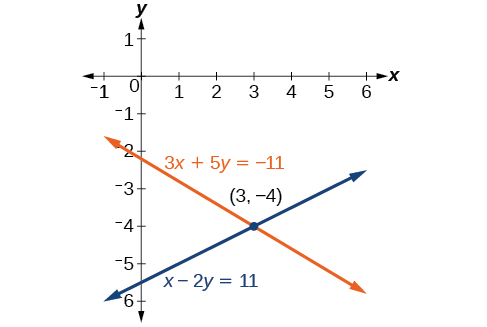
3x+5y=−11x−2y=11
Solución
Agregar estas ecuaciones tal como se presentan no eliminará una variable. No obstante, vemos que la primera ecuación tiene3x en ella y la segunda la tienex. Entonces, si multiplicamos la segunda ecuación por−3, los términos x sumarán a cero.
x−2y=11−3(x−2y)=−3(11)Multiply both sides by −3.−3x+6y=−33Use the distributive property.
Ahora, vamos a agregarlos.
3x+5y=−11−3x+6y_=−33_11y=−44y=−4
Para el último paso, sustituimosy=−4 en una de las ecuaciones originales y resolvemos parax.
3x+5y=−113x+5(−4)=−113x−20=−113x=9x=3
Nuestra solución es el par ordenado(3,−4). Ver Figura7.2.7. Verifique la solución en la segunda ecuación original.
x−2y=11(3)−2(−4)=3+8=11True
Resolver el sistema de ecuaciones por suma.
2x−7y=23x+y=−20
- Contestar
-
(−6,−2)
Resolver el sistema de ecuaciones dado en dos variables por suma.
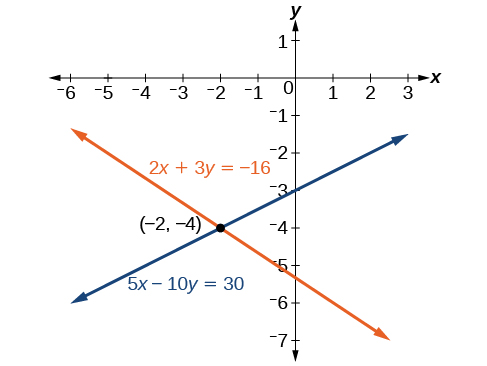
2x+3y=−165x−10y=30
Solución
Una ecuación tiene2x y la otra tiene5x. El múltiplo menos común es10x así que tendremos que multiplicar ambas ecuaciones por una constante para eliminar una variable. Eliminemosx multiplicando la primera ecuación por−5 y la segunda por2.
−5(2x+3y)=−5(−16)−10x−15y=802(5x−10y)=2(30)10x−20y=60
Después, sumamos las dos ecuaciones juntas.
−10x−15y=8010x−20y_=60_−35y=140y=−4
Sustituiry=−4 en la primera ecuación original.
2x+3(−4)=−162x−12=−162x=−4x=−2
La solución es(−2,−4). Compruébalo en la otra ecuación.
5x−10y=305(−2)−10(−4)=30−10+40=3030=30
Ver Figura7.2.8.
Resolver el sistema de ecuaciones dado en dos variables por suma.
x3+y6=3x2−y4=1
Solución
Primero borra cada ecuación de fracciones multiplicando ambos lados de la ecuación por el mínimo denominador común.
6(x3+y6)=6(3)2x+y=184(x2−y4)=4(1)2x−y=4
Ahora multiplique la segunda ecuación por−1 para que podamos eliminar la variable x.
−1(2x−y)=−1(4)−2x+y=−4
Sumar las dos ecuaciones para eliminar lax variable -y resolver la ecuación resultante.
2x+y=18−2x+y=−42y=14y=7
Sustituiry=7 en la primera ecuación.
2x+(7)=182x=11x=112=7.5
La solución es(112,7). Compruébalo en la otra ecuación.
x2−y4=11122−74=1114−74=144=1
Resolver el sistema de ecuaciones por suma.
2x+3y=83x+5y=10
- Contestar
-
(10,−4)
Identificación de sistemas inconsistentes de ecuaciones que contienen dos variables
Ahora que tenemos varios métodos para resolver sistemas de ecuaciones, podemos usar los métodos para identificar sistemas inconsistentes. Recordemos que un sistema inconsistente consiste en líneas paralelas que tienen la misma pendiente pero diferentes intercepciones y. Nunca se cruzarán. Al buscar una solución a un sistema inconsistente, se nos ocurrirá una declaración falsa, como12=0.
Resuelve el siguiente sistema de ecuaciones.
x=9−2yx+2y=13
Solución
Podemos abordar este problema de dos maneras. Debido a que una ecuación ya está resueltax, el paso más obvio es usar la sustitución.
x+2y=13(9−2y)+2y=139+0y=139=13
Claramente, esta afirmación es una contradicción porque9≠13. Por lo tanto, el sistema no tiene solución.
El segundo enfoque sería manipular primero las ecuaciones para que ambas estén en forma de pendiente-intercepción. Maniputamos la primera ecuación de la siguiente manera.
x=9−2y2y=−x+9y=−12x+92
Luego convertimos la segunda ecuación expresada en forma pendiente-intercepción.
x+2y=132y=−x+13y=−12x+132
Comparando las ecuaciones, vemos que tienen la misma pendiente pero diferentesy -intercepciones. Por lo tanto, las líneas son paralelas y no se cruzan.
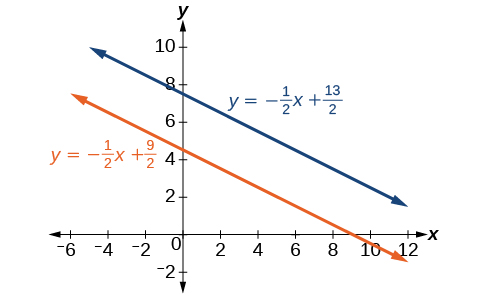
y=−12x+92y=−12x+132
Análisis
Escribir las ecuaciones en forma de pendiente-intersección confirma que el sistema es inconsistente porque todas las líneas se cruzarán eventualmente a menos que sean paralelas. Las líneas paralelas nunca se cruzarán; así, las dos líneas no tienen puntos en común. Las gráficas de las ecuaciones en este ejemplo se muestran en la Figura7.2.9.
Resolver el siguiente sistema de ecuaciones en dos variables.
2y−2x=22y−2x=6
- Contestar
-
Sin solución. Se trata de un sistema inconsistente.
Expresando la Solución de un Sistema de Ecuaciones Dependientes que Contiene Dos Variables
Recordemos que un sistema dependiente de ecuaciones en dos variables es un sistema en el que las dos ecuaciones representan la misma línea. Los sistemas dependientes tienen un número infinito de soluciones porque todos los puntos en una línea también están en la otra línea. Después de usar sustitución o adición, la ecuación resultante será una identidad, como0=0.
Encuentre una solución al sistema de ecuaciones utilizando el método de suma.
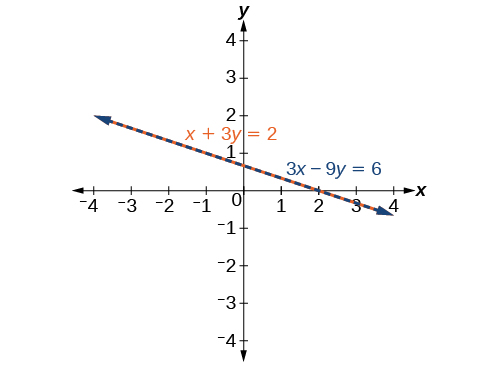
x+3y=23x+9y=6
Solución
Con el método de suma, queremos eliminar una de las variables sumando las ecuaciones. En este caso, centrémonos en eliminarx. Si multiplicamos ambos lados de la primera ecuación por−3, entonces podremos eliminar la variable x.
x+3y=2(−3)(x+3y)=(−3)(2)−3x−9y=−6
Ahora agregue las ecuaciones.
−3x−9y=−6+ 3x+9y_=6_0=0
Podemos ver que habrá un número infinito de soluciones que satisfagan ambas ecuaciones.
Análisis
Si reescribimos ambas ecuaciones en la forma pendiente-intercepción, podríamos saber cómo sería la solución antes de agregar. Veamos qué sucede cuando convertimos el sistema a forma de pendiente-intercepción.
x+3y=23y=−x+2y=−13x+233x+9y=69y=−3x+6y=−39x+69y=−13x+23
Ver Figura7.2.10. Observe que los resultados son los mismos. La solución general al sistema es(x,−13x+23).
Resolver el siguiente sistema de ecuaciones en dos variables.
y−2x=5−3y+6x=−15
- Contestar
-
El sistema es dependiente por lo que hay infinitas soluciones de la forma(x,2x+5).
Usando Sistemas de Ecuaciones para Investigar Ganancias
Utilizando lo que hemos aprendido sobre los sistemas de ecuaciones, podemos volver al problema de fabricación de monopatines al inicio de la sección. La función de ingresos del fabricante de monopatines es la función utilizada para calcular la cantidad de dinero que entra en el negocio. Se puede representar por la ecuaciónR=xp, dondex =cantidad yp =precio. La función de ingresos se muestra en naranja en la Figura7.2.11.
La función de costo es la función utilizada para calcular los costos de hacer negocios. Incluye costos fijos, como renta y salarios, y costos variables, como servicios públicos. La función de costo se muestra en azul en la Figura7.2.11. Elx eje -representa la cantidad en cientos de unidades. Ely eje -representa ya sea costo o ingresos en cientos de dólares.
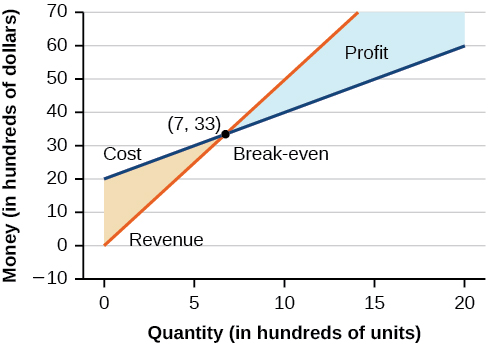
El punto en el que se cruzan las dos líneas se denomina punto de equilibrio. Podemos ver en la gráfica que si se producen700 unidades, el costo es$3,300 y los ingresos también lo son$3,300. Es decir, la compañía se rompe aunque produzcan y vendan700 unidades. Ni ganan dinero ni pierden dinero.
La región sombreada a la derecha del punto de equilibrio representa cantidades por las que la empresa obtiene ganancias. La región sombreada a la izquierda representa cantidades por las que la empresa sufre una pérdida. La función de ganancia es la función de ingresos menos la función de costo, escrita comoP(x)=R(x)−C(x). Claramente, conocer la cantidad por la que el costo equivale a los ingresos es de gran importancia para las empresas.
Dada la función de costoC(x)=0.85x+35,000 y la función de ingresosR(x)=1.55x, encuentre el punto de equilibrio y la función de ganancia.
Solución
Escribe el sistema de ecuaciones usandoy para reemplazar la notación de función.
y=0.85x+35,000y=1.55x
Sustituir la expresión0.85x+35,000 de la primera ecuación por la segunda ecuación y resolver parax.
0.85x+35,000=1.55x35,000=0.7x50,000=x
Entonces, sustituimos ya seax=50,000 en la función de costo o en la función de ingresos.
1.55(50,000)=77,500
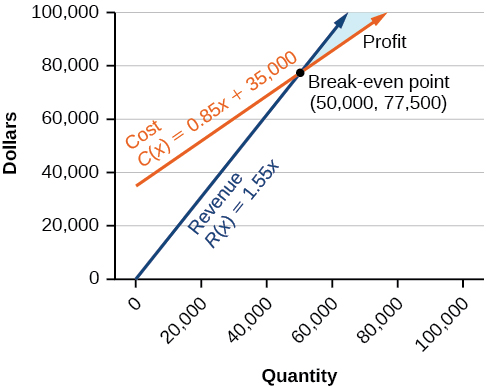
El punto de equilibrio es(50,000,77,500).
La función de beneficio se encuentra usando la fórmulaP(x)=R(x)−C(x).
P(x)=1.55x−(0.85x+35,000)=0.7x−35,000
La función de ganancia esP(x)=0.7x−35,000.
Análisis
El costo para producir50,000 unidades es$77,500, y los ingresos por las ventas de50,000 unidades también lo son$77,500. Para obtener ganancias, el negocio debe producir y vender más que50,000 unidades. Ver Figura7.2.12.
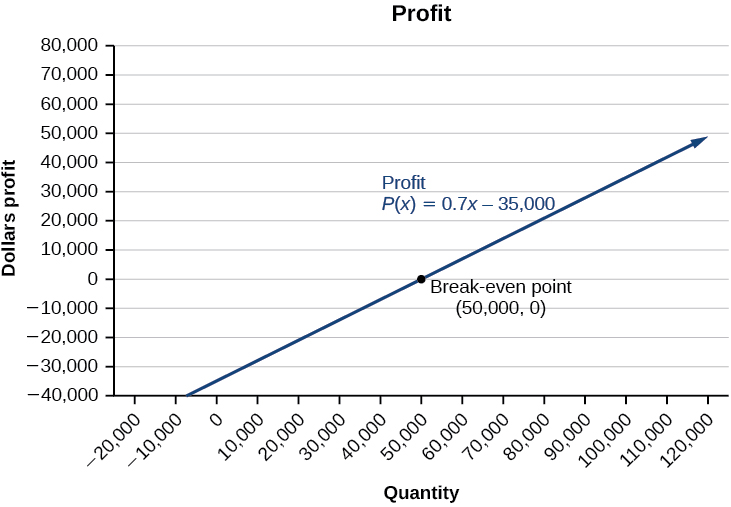
Vemos a partir de la gráfica en Figura7.2.13 que la función de ganancia tiene un valor negativo hastax=50,000, cuando la gráfica cruza elx eje -eje. Entonces, la gráfica emerge eny valores positivos y continúa en este camino ya que la función de ganancia es una línea recta. Esto ilustra que el punto de equilibrio para las empresas ocurre cuando la función de ganancia es0. El área a la izquierda del punto de equilibrio representa operar con pérdidas.
El costo de un boleto al circo es$25.00 para niños y$50.00 para adultos. En un día determinado, la asistencia al circo es2,000 y el ingreso total de la puerta es$70,000. ¿Cuántos niños y cuántos adultos compraron boletos?
Solución
Letc = el número de niños ya = el número de adultos que asisten.
El número total de personas es2,000. Podemos usar esto para escribir una ecuación para el número de personas en el circo ese día.
c+a=2,000
Los ingresos de todos los niños se pueden encontrar multiplicando$25.00 por el número de hijos,25c. Los ingresos de todos los adultos se pueden encontrar multiplicando$50.00 por el número de adultos,50a. El ingreso total es$70,000. Podemos usar esto para escribir una ecuación para los ingresos.
25c+50a=70,000
Ahora tenemos un sistema de ecuaciones lineales en dos variables.
c+a=2,000
25c+50a=70,000
En la primera ecuación, el coeficiente de ambas variables es1. Podemos resolver rápidamente la primera ecuación para cualquierac oa. Vamos a resolver paraa.
c+a=2,000a=2,000−c
Sustituir la expresión2,000−c en la segunda ecuación foroa y resolver parac.
25c+50(2,000−c)=70,00025c+100,000−50c=70,000−25c=−30,000c=1,200
Sustituirc=1,200 en la primera ecuación para resolvera.
\begin{align*} 1,200+a &= 2,000 \\ a &= 800 \end{align*}
Encontramos que1,200 niños y800 adultos compraron boletos para el circo ese día.
Boletos de comida al costo del circo$4.00 para niños y$12.00 para adultos. Si se compraron boletos de1,650 comida para un total de$14,200,, ¿cuántos niños y cuántos adultos compraron boletos de comida?
- Contestar
-
700niños,950 adultos
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con sistemas de ecuaciones lineales.
Conceptos clave
- Un sistema de ecuaciones lineales consiste en dos o más ecuaciones compuestas por dos o más variables de manera que todas las ecuaciones del sistema se consideran simultáneamente.
- La solución a un sistema de ecuaciones lineales en dos variables es cualquier par ordenado que satisfaga cada ecuación de forma independiente. Ver Ejemplo\PageIndex{1}.
- Los sistemas de ecuaciones se clasifican como independientes con una solución, dependientes con un número infinito de soluciones, o inconsistentes con ninguna solución.
- Un método para resolver un sistema de ecuaciones lineales en dos variables es graficando. En este método, graficamos las ecuaciones en el mismo conjunto de ejes. Ver Ejemplo\PageIndex{2}.
- Otro método para resolver un sistema de ecuaciones lineales es por sustitución. En este método, resolvemos para una variable en una ecuación y sustituimos el resultado en la segunda ecuación. Ver Ejemplo\PageIndex{3}.
- Un tercer método para resolver un sistema de ecuaciones lineales es por adición, en el que podemos eliminar una variable sumando coeficientes opuestos de las variables correspondientes. Ver Ejemplo\PageIndex{4}.
- A menudo es necesario multiplicar una o ambas ecuaciones por una constante para facilitar la eliminación de una variable al sumar las dos ecuaciones juntas. Ver Ejemplo\PageIndex{5}\PageIndex{6}, Ejemplo y Ejemplo\PageIndex{7}.
- Cualquiera de los dos métodos de resolución de un sistema de ecuaciones da como resultado una declaración falsa para sistemas inconsistentes porque están formados por líneas paralelas que nunca se cruzan. Ver Ejemplo\PageIndex{8}.
- La solución a un sistema de ecuaciones dependientes siempre será cierta porque ambas ecuaciones describen la misma línea. Ver Ejemplo\PageIndex{9}.
- Los sistemas de ecuaciones se pueden utilizar para resolver problemas del mundo real que involucran más de una variable, como los relacionados con ingresos, costos y ganancias. Ver Ejemplo\PageIndex{10} y Ejemplo\PageIndex{11}.


