7.9: Resolver sistemas con la regla de Cramer
- Page ID
- 117025
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Evaluar 2 × 2 determinantes.
- Usa la Regla de Cramer para resolver un sistema de ecuaciones en dos variables.
- Evaluar 3 × 3 determinantes.
- Usa la Regla de Cramer para resolver un sistema de tres ecuaciones en tres variables.
- Conocer las propiedades de los determinantes.
Hemos aprendido a resolver sistemas de ecuaciones en dos variables y tres variables, y por múltiples métodos: sustitución, adición, eliminación gaussiana, usando la inversa de una matriz y graficando. Algunos de estos métodos son más fáciles de aplicar que otros y son más apropiados en ciertas situaciones. En esta sección, estudiaremos dos estrategias más para resolver sistemas de ecuaciones.
Evaluando el Determinante de una Matriz de 2 × 2
Un determinante es un número real que puede ser muy útil en matemáticas porque tiene múltiples aplicaciones, como calcular área, volumen y otras cantidades. Aquí, utilizaremos determinantes para revelar si una matriz es invertible mediante el uso de las entradas de una matriz cuadrada para determinar si existe una solución al sistema de ecuaciones. Quizás una de las aplicaciones más interesantes, sin embargo, es su uso en criptografía. Las señales o mensajes seguros a veces se envían codificados en una matriz. Los datos sólo pueden ser descifrados con una matriz invertible y el determinante. Para nuestros propósitos, nos enfocamos en el determinante como una indicación de la invertibilidad de la matriz. Calcular el determinante de una matriz implica seguir los patrones específicos que se describen en esta sección.
El determinante de una matriz de 2 × 2, dada
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
se define como

Observe el cambio en la notación. Existen varias formas de indicar el determinante, incluyendo\(\det(A)\) y reemplazando los corchetes en una matriz con líneas rectas,\(| A |\).
Encontrar el determinante de la matriz dada.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Solución
\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]
Uso de la regla de Cramer para resolver un sistema de dos ecuaciones en dos variables
Ahora vamos a introducir un método final para resolver sistemas de ecuaciones que utilizan determinantes. Conocida como Regla de Cramer, esta técnica se remonta a mediados del siglo XVIII y lleva el nombre de su innovador, el matemático suizo Gabriel Cramer (1704-1752), quien la introdujo en 1750 en Introduction à l'Analyse des lignes Courbes algébriques. La Regla de Cramer es un método viable y eficiente para encontrar soluciones a sistemas con un número arbitrario de incógnitas, siempre que tengamos el mismo número de ecuaciones que incógnitas.
La Regla de Cramer nos dará la solución única a un sistema de ecuaciones, si existe. No obstante, si el sistema no tiene solución o un número infinito de soluciones, esto será indicado por un determinante de cero. Para saber si el sistema es inconsistente o dependiente, habrá que utilizar otro método, como la eliminación.
Para entender la regla de Cramer, veamos de cerca cómo resolvemos sistemas de ecuaciones lineales usando operaciones básicas de fila. Considerar un sistema de dos ecuaciones en dos variables.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Eliminamos una variable usando operaciones de fila y resolvemos para la otra. Decir que deseamos resolver para\(x\). Si la Ecuación\ ref {eq2} se multiplica por lo opuesto al coeficiente de\(y\) en la Ecuación\ ref {eq1}, la Ecuación\ ref {eq1} se multiplica por el coeficiente de\(y\) en la Ecuación\ ref {eq2}, y agregamos las dos ecuaciones, la variable\(y\) será eliminada.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Multiply }R_1 \text{ by }b_2 \\ -&\underline{b_1a_2x−b_1b_2y=−b_1c_2} & \text{Multiply }R_2 \text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]
Ahora, resuelve para\(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
De igual manera, para resolver para\(y\), vamos a eliminar\(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x−a_1b_2y=−a_1c_2} & \text{Multiply }R_2 \text{ by }−a_1 \\ & a_2b_1y−a_1b_2y =a_2c_1−a_1c_2 \end{align*}\]
Resolviendo para\(y\) da
\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Observe que el denominador para ambos\(x\) y\(y\) es el determinante de la matriz de coeficientes.
Podemos usar estas fórmulas para resolver por\(x\) y\(y\), pero la regla de Cramer también introduce nueva notación:
- \(D\):determinante de la matriz de coeficientes
- \(D_x\):determinante del numerador en la solución de\(x\)
\[x=\dfrac{D_x}{D}\]
- \(D_y\):determinante del numerador en la solución de\(y\)
\[y=\dfrac{D_y}{D}\]
La clave de la Regla de Cramer es sustituir la columna variable de interés por la columna constante y calcular los determinantes. Entonces podemos expresar\(x\) y\(y\) como cociente de dos determinantes.
La regla de Cramer es un método que utiliza determinantes para resolver sistemas de ecuaciones que tienen el mismo número de ecuaciones que las variables.
Considera un sistema de dos ecuaciones lineales en dos variables.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
La solución que utiliza la regla de Cramer se da como
\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0 \end{align}\]
Si estamos resolviendo para\(x\), la\(x\) columna se sustituye por la columna constante. Si estamos resolviendo para\(y\), la\(y\) columna se sustituye por la columna constante.
Resuelve el siguiente\(2 × 2\) sistema usando la Regla de Cramer.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Solución
Resolver para\(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]
Resolver para\(y\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align*}\]
La solución es\((2,−3)\).
Usa la Regla de Cramer para resolver el\(2 × 2\) sistema de ecuaciones.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Contestar
-
\((3,−7)\)
Evaluando el Determinante de una Matriz de 3 × 3
Encontrar el determinante de una matriz 2×2 es sencillo, pero encontrar el determinante de una matriz 3×3 es más complicado. Un método es aumentar la matriz 3×3 con una repetición de las dos primeras columnas, dando una matriz de 3×5. Después calculamos la suma de los productos de entradas hacia abajo cada una de las tres diagonales (superior izquierda a inferior derecha), y restamos los productos de entradas hacia arriba cada una de las tres diagonales (inferior izquierda a superior derecha). Esto se entiende más fácilmente con un visual y un ejemplo.
Encuentra el determinante de la matriz 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- Aumente\(A\) con las dos primeras columnas.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- De la parte superior izquierda a la derecha inferior: Multiplica las entradas por la primera diagonal. Agregar el resultado al producto de entradas abajo de la segunda diagonal. Agrega este resultado al producto de las entradas por la tercera diagonal.
- De inferior izquierda a superior derecha: Restar el producto de entradas hasta la primera diagonal. De este resultado restar el producto de entradas hasta la segunda diagonal. De este resultado, restar el producto de entradas hasta la tercera diagonal.
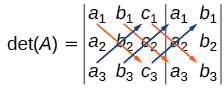
El álgebra es el siguiente:
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Encontrar el determinante de la\(3 × 3\) matriz dada
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Solución
Aumente la matriz con las dos primeras columnas y luego siga la fórmula. Por lo tanto,
\[\begin{align*} | A | &= \left| \begin{array}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{array}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Encuentra el determinante de la matriz 3×3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Contestar
-
\(−10\)
No, este método sólo funciona para matrices de 2 × 2 y 3 × 3. Para matrices más grandes, lo mejor es usar una utilidad gráfica o un software de computadora.
Uso de la regla de Cramer para resolver un sistema de tres ecuaciones en tres variables
Ahora que podemos encontrar el determinante de una\(3 × 3\) matriz, podemos aplicar la Regla de Cramer para resolver un sistema de tres ecuaciones en tres variables. La Regla de Cramer es sencilla, siguiendo un patrón consistente con la Regla de Cramer para\(2 × 2\) matrices. A medida que aumenta el orden de la matriz a\(3 × 3\), sin embargo, se requieren muchos más cálculos.
Cuando calculamos que el determinante es cero, la Regla de Cramer no da ninguna indicación de si el sistema no tiene solución o un número infinito de soluciones. Para averiguarlo, tenemos que realizar la eliminación en el sistema.
Considera un\(3 × 3\) sistema de ecuaciones.
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue}d_3 \\ \end{align}\]
\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\),\(D≠0\)
donde
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Si estamos escribiendo el determinante\(D_x\), reemplazamos la\(x\) columna por la columna constante. Si estamos escribiendo el determinante\(D_y\), reemplazamos ellos y columna por la columna constante. Si estamos escribiendo el determinante\(D_z\), reemplazamos la\(z\) columna por la columna constante. Siempre revisa la respuesta.
Encuentra la solución al\(3 × 3\) sistema dado usando la Regla de Cramer.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Solución
Usa la Regla de Cramer.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\),\(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\\14&3&−2\end{vmatrix}\),\(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\),\(D_z=\begin{vmatrix}1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)
Entonces,
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
La solución es\((1,3,−2)\).
Usa la Regla de Cramer para resolver la\(3 × 3\) matriz.
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Contestar
-
\(\left(−2,\dfrac{3}{5},\dfrac{12}{5}\right)\)
Resuelve el sistema de ecuaciones usando la Regla de Cramer.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Solución
Comenzamos por encontrar los determinantes\(D\),\(D_x\), y\(D_y\).
\(D=\begin{vmatrix}3&−2\\6&−4\end{vmatrix}=3(−4)−6(−2)=0\)
Sabemos que un determinante de cero significa que o bien el sistema no tiene solución o tiene un número infinito de soluciones. Para ver cuál, utilizamos el proceso de eliminación. Nuestro objetivo es eliminar una de las variables.
- Multiplicar la ecuación\ ref {eq3} por\(−2\).
- Agrega el resultado a Ecuación\ ref {eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\;\;\;\;\; 0=−8 \end{align*}\]
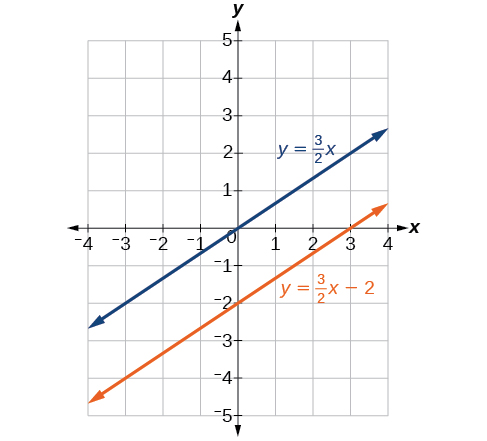
Obtenemos la ecuación\(0=−8\), que es falsa. Por lo tanto, el sistema no tiene solución. Graficar el sistema revela dos líneas paralelas. Ver Figura\(\PageIndex{1}\).
Resuelve el sistema con un número infinito de soluciones.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end{align}\]
Solución
Encontremos primero el determinante. Configura una matriz aumentada por las dos primeras columnas.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)
Entonces,
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1)−6(3)(−2)=0\)
Como el determinante es igual a cero, o no hay solución o un número infinito de soluciones. Tenemos que realizar la eliminación para averiguarlo.
1. Multiplica la ecuación\ ref {eq5} por\(−2\) y agrega el resultado a la ecuación\ ref {eq7}:
\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]
2. Obtener una respuesta de\(0=0\), una afirmación que siempre es cierta, significa que el sistema tiene un número infinito de soluciones. Graficando el sistema, podemos ver que dos de los planos son iguales y ambos se cruzan con el tercer plano en una línea. Ver Figura\(\PageIndex{2}\).
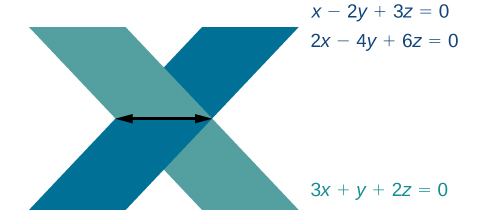
Comprensión de las propiedades de los determinantes
Hay muchas propiedades de los determinantes. Aquí se enumeran algunas propiedades que pueden ser útiles para calcular el determinante de una matriz.
- Si la matriz está en forma triangular superior, el determinante es igual al producto de entradas abajo de la diagonal principal.
- Cuando se intercambian dos filas, el determinante cambia de signo.
- Si dos filas o dos columnas son idénticas, el determinante es igual a cero.
- Si una matriz contiene una fila de ceros o una columna de ceros, el determinante es igual a cero.
- El determinante de una matriz inversa\(A^{−1}\) es el recíproco del determinante de la matriz\(A\).
- Si alguna fila o columna se multiplica por una constante, el determinante se multiplica por el mismo factor.
Ilustrar cada una de las propiedades de los determinantes.
Solución
La propiedad 1 establece que si la matriz está en forma triangular superior, el determinante es el producto de las entradas hacia abajo de la diagonal principal.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)
Aumente\(A\) con las dos primeras columnas.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)
Entonces
\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1(0)(2)\\ &= -2 \end{align*}\]
La propiedad 2 establece que el intercambio de filas cambia el signo. Dado
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)(5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]
La propiedad 3 establece que si dos filas o dos columnas son idénticas, el determinante es igual a cero.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{array}\right]\\ \det(A)&=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\\ &=4-4+8+4-4-8\\ &=0 \end{align*}\]
La propiedad 4 establece que si una fila o columna es igual a cero, el determinante es igual a cero. Por lo tanto,
\[\begin{align*} A&=\begin{bmatrix}1&2\\0&0\end{bmatrix}\\ \det(A)&=1(0)-2(0)\\ &=0 \end{align*}\]
La propiedad 5 establece que el determinante de una matriz inversa\(A^{−1}\) es el recíproco del determinante\(A\). Por lo tanto,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-3(2)\\ &=-2 \end{align*}\]
\[\begin{align*} A^{-1}&=\begin{bmatrix}-2&1\\\dfrac{3}{2}&-\dfrac{1}{2}\end{bmatrix}\\ \det(A^{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \end{align*}\]
La propiedad 6 establece que si alguna fila o columna de una matriz se multiplica por una constante, el determinante se multiplica por el mismo factor. Por lo tanto,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \end{align*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4)\\ &=-4 \end{align*}\]
Encuentre la solución al\(3 × 3\) sistema dado.
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\end{align}\]
Solución
Usando la regla de Cramer, tenemos
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Observe que la segunda y tercera columnas son idénticas. De acuerdo con la Propiedad 3, el determinante será cero, por lo que no hay solución o un número infinito de soluciones. Tenemos que realizar la eliminación para averiguarlo.
1. Multiplica la Ecuación\ ref {eq10} por\(–2\) y agrega el resultado a la Ecuación\ ref {eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
Obtener una declaración que es una contradicción significa que el sistema no tiene solución.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con la Regla de Cramer.
Conceptos clave
- El determinante para\(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) es\(ad−bc\). Ver Ejemplo\(\PageIndex{1}\).
- La regla de Cramer reemplaza una columna variable por la columna constante. Las soluciones son\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\). Ver Ejemplo\(\PageIndex{2}\).
- Para encontrar el determinante de una\(3×3\) matriz, aumentar con las dos primeras columnas. Sumar las tres entradas diagonales (superior izquierda a inferior derecha) y restar las tres entradas diagonales (inferior izquierda a superior derecha). Ver Ejemplo\(\PageIndex{3}\).
- Para resolver un sistema de tres ecuaciones en tres variables usando la Regla de Cramer, reemplace una columna variable por la columna constante para cada solución deseada:\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\). Ver Ejemplo\(\PageIndex{4}\).
- La Regla de Cramer también es útil para encontrar la solución de un sistema de ecuaciones sin solución ni soluciones infinitas. Ver Ejemplo\(\PageIndex{5}\) y Ejemplo\(\PageIndex{6}\).
- Ciertas propiedades de los determinantes son útiles para resolver problemas. Por ejemplo:
- Si la matriz está en forma triangular superior, el determinante es igual al producto de entradas abajo de la diagonal principal.
- Cuando se intercambian dos filas, el determinante cambia de signo.
- Si dos filas o dos columnas son idénticas, el determinante es igual a cero.
- Si una matriz contiene una fila de ceros o una columna de ceros, el determinante es igual a cero.
- El determinante de una matriz inversa\(A^{−1}\) es el recíproco del determinante de la matriz\(A\).
- Si alguna fila o columna se multiplica por una constante, el determinante se multiplica por el mismo factor. Ver Ejemplo\(\PageIndex{7}\) y Ejemplo\(\PageIndex{8}\).


