Inicio
Matemáticas
Álgebra Abstracta y Geométrica
Álgebra Geométrica Aplicada (Tisza)
1: Preliminares algebraicos
1.2: La geometría del grupo de rotación tridimensional. El teorema de Rodrígues-Hamilton

1.2: La geometría del grupo de rotación tridimensional. El teorema de Rodrígues-Hamilton

Última actualización
Guardar como PDF

Page ID: 110026

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hay tres tipos de transformaciones que mapean el espacio euclidiano sobre sí mismo: las traducciones, las rotaciones y las inversiones. La notación estándar para el grupo de rotación adecuado es$\mathcal{O}^{+}$, o$\mathcal{SO}(3)$, abreviatura de “grupo ortogonal simple en tres dimensiones”. “Simple” significa que el determinante de la transformación es$+1$, tenemos rotaciones adecuadas con la exclusión de la inversión de las coordenadas:

\[\begin{array} {c} {x \rightarrow -x}\\ {y \rightarrow -y}\\ {z \rightarrow -z} \end{array}\]

problema al que volveremos más tarde.

En contraste con el grupo de traducciones,$\mathcal{SO}(3)$ es no abeliano, y su teoría, comenzando con la adecuada elección de parámetros, es bastante complicada. Sin embargo, su teoría fue desarrollada en un grado notable durante el siglo XVIII por Euler.

Dentro de la mecánica clásica no se considera de fundamental importancia el problema de la rotación. El formalismo hamiltoniano se expresa generalmente en términos de masas puntuales, que no rotan. Hay un sesgo incorporado a favor del movimiento traslacional.

La situación es diferente en la mecánica cuántica donde la rotación juega un papel primordial. Tenemos buenas razones para darle atención temprana al grupo de rotación, aunque en este punto tenemos que limitarnos a una discusión puramente geométrica que luego se pondrá en forma algebraica.

Según un conocido teorema de Euler, un desplazamiento arbitrario de un cuerpo rígido con un solo punto fijo puede concebirse como una rotación alrededor de un eje fijo que puede especificarse en términos del ángulo de rotación$\phi$, y el vector unitario$\hat{u}$ a lo largo de la dirección del eje de rotación. Convencionalmente, el sentido de rotación está determinado por la regla de la mano derecha. Simbólicamente podemos escribir$R = \{\hat{u}, \phi\}$.

El primer paso para describir la estructura del grupo es proporcionar una regla para la composición de las rotaciones teniendo debidamente en cuenta el carácter de no desplazamiento de esta operación. La esencia del argumento está contenida en un antiguo teorema de Rodrigues-Hamilton.

Nuestra presentación sigue la de C. L. K. Whitney [Whi68]. Considera los productos

\[\begin{array}{c} {R_{3} = R_{2}R_{1}} \end{array}\]

\[\begin{array}{c} {R'_{3} = R_{1}R_{2}} \end{array} \label{EQ1.2.3}\]

donde$R_{3}$ es la rotación compuesta en la que$R_{1}$ va seguida de$R_{2}$.

La Figura 1.1 representa la esfera unitaria y se construye de la siguiente manera: los puntos finales de los vectores$\hat{u}_{1}$, y$\hat{u}_{2}$ determinan un gran círculo, cuyo arco más pequeño forma la base de triángulos de imagen especular que tienen ángulos$\phi_{1} / 2$ y$\phi_{2} / 2$ como se indica. El punto final del vector$\hat{u}'_{1}$ se localiza por rotación$\hat{u}_{1}$, por ángulo$\phi_{2}$ alrededor$\hat{u}_{2}$. Nuestra afirmación, de que las demás cantidades que aparecen en la figura están legítimamente etiquetadas$\phi_{3} / 2$,$\hat{u}_{3} , \hat{u}'_{3}$ se fundamenta fácilmente. Siguiendo la secuencia de operaciones señalada en 2.2.3, vemos que el vector llamado$\hat{u}_{3}$, primero se gira por ángulo$\phi_{1}$, aproximadamente$\hat{u}_{1}$, que toma en$\hat{u}'_{3}$. Después se gira por ángulo$\phi_{2}$ alrededor$\hat{u}_{2}$, lo que lo lleva de nuevo a$\hat{u}_{3}$. Al ser invariante, es efectivamente el eje de la rotación combinada. Además, vemos que la primera rotación deja$\hat{u}_{1}$, invariante y la segunda rotación, que aproximadamente$\hat{u}_{2}$, la lleva a$\hat{u}'_{1}$, la posición que alcanzaría si simplemente girara alrededor$\hat{u}_{3}$, por el ángulo llamado$\phi_{3}$. Así, ese ángulo es efectivamente el ángulo de la rotación combinada. Tenga en cuenta que un argumento simétrico muestra que$\hat{u}'_{3}$ y$\phi_{3}$ son el eje y ángulo de la rotación$P'_{3} = R_{1}R_{2}$.

La ecuación\ ref {EQ1.2.3} se puede expresar también como

\[\begin{array}{c} {R^{-1}_{3}R_{2}R_{1} = 1} \end{array}\]

que se interpreta de la siguiente manera: rotación alrededor$\hat{u}_{1}$, por$\phi_{1}$, seguida de rotación alrededor$\hat{u}_{2}$, por$\phi_{2}$, seguida de rotación alrededor$\hat{u}_{3}$, por menos$\phi_{3}$, no produce ningún cambio. Esta afirmación es el teorema de Rodrígues-Hamilton.

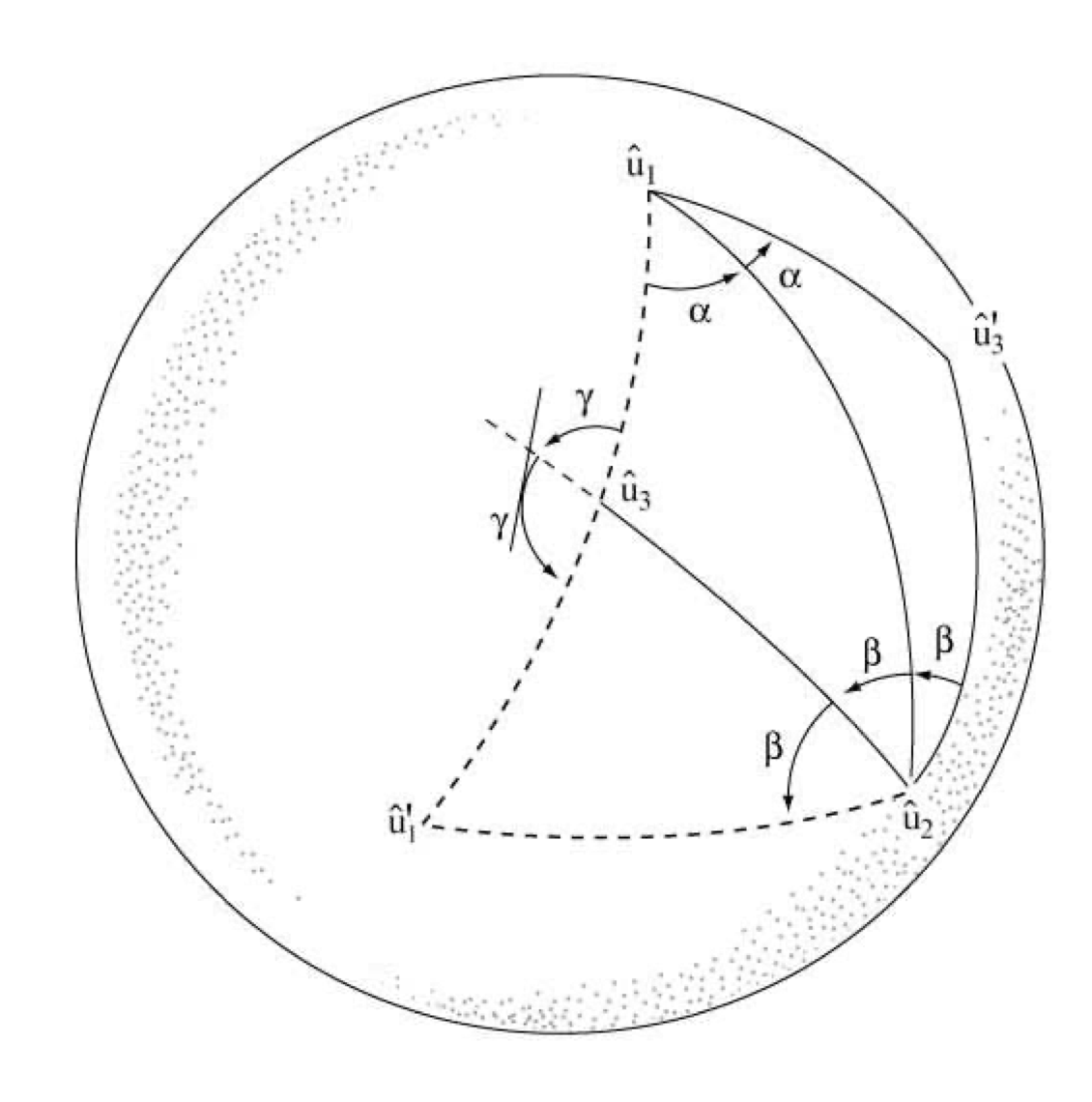
$Screen Shot 2020-07-04 at 3.37.01 PM.png$

Figura 1.1: Composición de las Rotaciones de la Esfera. $\alpha = \phi_{1}/2, \beta = \phi_{2}/2, \gamma = \phi_{3}/2$.