19.1: Celosías

Última actualización
Guardar como PDF

Page ID: 111268

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Conjuntos parcialmente ordenados

Comenzamos el estudio de las celosías y álgebras booleanas generalizando la idea de desigualdad. Recordemos que una relación en un conjunto$X$ es un subconjunto de$X \times X\text{.}$ Una relación$P$ on$X$ se llama un orden parcial de$X$ si satisface los siguientes axiomas.

La relación es reflexiva:$(a, a) \in P$ para todos$a \in X\text{.}$
La relación es antisimétrica: si$(a,b) \in P$ y$(b,a) \in P\text{,}$ entonces$a = b\text{.}$
La relación es transitiva: si$(a, b) \in P$ y$(b, c) \in P\text{,}$ entonces$(a, c) \in P\text{.}$

Normalmente escribiremos$a \preceq b$ para significar a$(a, b) \in P$ menos que algún símbolo esté naturalmente asociado con un orden parcial particular, como$a \leq b$ con números enteros$a$ y$b\text{,}$ o$A \subset B$ con conjuntos$A$ y$B\text{.}$ Un conjunto$X$ junto con un orden parcial$\preceq$ es llamado conjunto parcialmente ordenado, o poset.

Ejemplo$19.1$

El conjunto de enteros (o racionales o reales) es un poset donde

Solución

$a \leq b$tiene el significado habitual para dos enteros$a$ y$b$ en${\mathbb Z}\text{.}$

Ejemplo$19.2$

Dejar$X$ ser cualquier conjunto. Vamos a definir el conjunto de potencia de$X$ para que sea el conjunto de todos los subconjuntos de$X\text{.}$ Denotamos el conjunto de potencia de$X$ por${\mathcal P}(X)\text{.}$ Por ejemplo, let$X = \{ a, b, c \}\text{.}$ Entonces

Solución

${\mathcal P}(X)$es el conjunto de todos los subconjuntos del conjunto$\{ a, b, c \}\text{:}$

\ begin {align*} &\\ emptyset & &\ {a\} & &\ {b\} & &\ {c\} &\\\ &\ {a, b\} & &\ {a, c\} & &\ {b, c\} & &\ {a, b, c\}. &\ end {alinear*}

En cualquier conjunto de potencia de un$X\text{,}$ conjunto de inclusión de conjunto,$\subset\text{,}$ es un orden parcial. Podemos representar el orden en$\{ a, b, c \}$ forma esquemática mediante un diagrama como el de la Figura$19.3$.

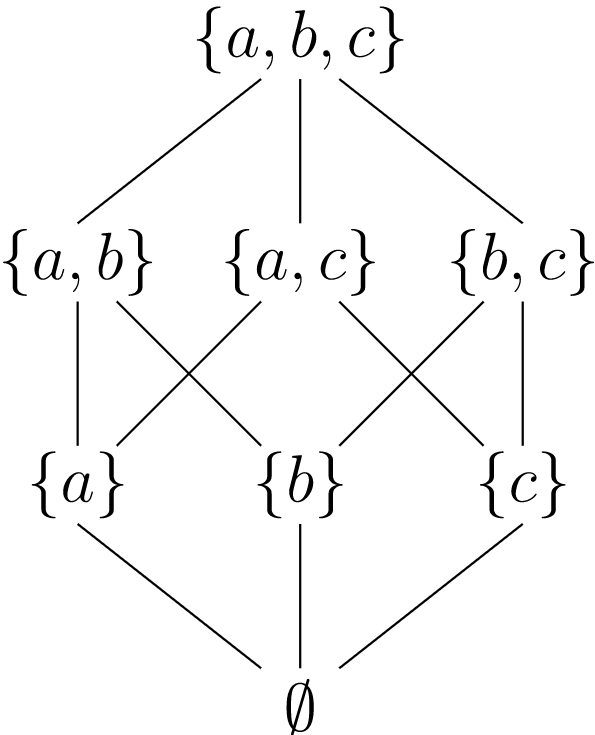
$clipboard_e1d09ee3865d3306295195b4aba0056b1.png$

$Figure \text { } 19.3.$Orden parcial en$\mathcal P( \{ a, b, c \})$

Ejemplo$19.4$

Seamos$G$ un grupo. El conjunto de subgrupos de$G$ es un

Solución

poset, donde se establece el orden parcial de inclusión.

Ejemplo$19.5$

Puede haber más de un pedido parcial en un conjunto en particular. Podemos formar un orden parcial sobre${\mathbb N}$$a \preceq b$ si$a \mid b\text{.}$ La relación es ciertamente reflexiva ya que$a \mid a$ para todos$a \in {\mathbb N}\text{.}$ Si$m \mid n$ y$n \mid m\text{,}$ entonces

Solución

$m = n\text{;}$de ahí que la relación sea también antisimétrica. La relación es transitiva, porque si$m \mid n$ y$n \mid p\text{,}$ entonces$m \mid p\text{.}$

Ejemplo$19.6$

Dejar$X = \{ 1, 2, 3, 4, 6, 8, 12, 24 \}$ ser el conjunto de divisores de$24$ con el orden parcial definido en Ejemplo$19.5$.

Solución

La figura$19.7$ muestra el orden parcial en$X\text{.}$

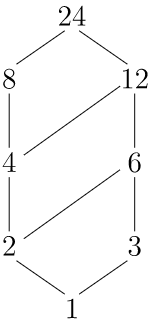
$clipboard_e099c47b3f4c6fc4ff388d9f18863e5bc.png$

$Figure \text { } 19.7.$Un orden parcial en los divisores de$24$

Dejar$Y$ ser un subconjunto de un poset$X\text{.}$ Un elemento$u$ en$X$ es un límite superior de$Y$ si$a \preceq u$ para cada elemento$a \in Y\text{.}$ Si$u$ es un límite superior de$Y$ tal que$u \preceq v$ para cada otro límite superior$v$ de $Y\text{,}$entonces$u$ se llama límite inferior superior o supremum de$Y\text{.}$ Un elemento$l$ en$X$ se dice que es un límite inferior de$Y$ si$l \preceq a$ para todos$a \in Y\text{.}$ Si $l$es un límite inferior de$Y$ tal que$k \preceq l$ por cada otro límite inferior$k$ de$Y\text{,}$ entonces$l$ se llama un mayor límite inferior o infimum de$Y\text{.}$

Ejemplo$19.8$

Dejar$Y = \{ 2, 3, 4, 6 \}$ estar contenido en el conjunto$X$ de Ejemplo$19.6$. Entonces

Solución

$Y$tiene límites superiores$12$ y$24\text{,}$ con$12$ como mínimo límite superior. El único límite inferior es,$1\text{;}$ por lo tanto, debe ser un límite inferior mayor.

Resulta que los límites menores superiores y los mayores límites inferiores son únicos si existen.

Teorema$19.9$

Dejar$Y$ ser un subconjunto no vacío de un poset$X\text{.}$ Si$Y$ tiene un límite inferior superior, entonces$Y$ tiene un límite superior mínimo único. Si$Y$ tiene un límite inferior mayor, entonces$Y$ tiene un límite inferior más grande único.

Prueba: Dejar$u_1$ y$u_2$ ser menos límites superiores para$Y\text{.}$ Por la definición del límite inferior superior,$u_1 \preceq u$ para todos los límites superiores$u$ de$Y\text{.}$ En particular,$u_1 \preceq u_2\text{.}$ Similarmente,$u_2 \preceq u_1\text{.}$ Por lo tanto,$u_1 = u_2$ por antisimetría. Un argumento similar muestra que el mayor límite inferior es único.

En muchos posets es posible definir operaciones binarias utilizando el mayor límite inferior y el límite menor superior de dos elementos. Una celosía es un poset$L$ tal que cada par de elementos$L$ tiene un límite mínimo superior y un límite inferior mayor. El límite inferior inferior de$a, b \in L$ se llama la unión de$a$ y$b$ y se denota por$a \vee b\text{.}$ El límite inferior más grande de$a, b \in L$ se llama el encuentro de$a$ y$b$ y se denota por$a \wedge b\text{.}$

Ejemplo$19.10$

$X$Déjese ser un conjunto. Entonces el conjunto de potencia de$X\text{,}$${\mathcal P}(X)\text{,}$ es una celosía. Para dos juegos

Solución

$A$y$B$ en${\mathcal P}(X)\text{,}$ el límite inferior superior de$A$ y$B$ es$A \cup B\text{.}$ Ciertamente$A \cup B$ es un límite superior de$A$ y$B\text{,}$ desde$A \subset A \cup B$ y$B \subset A \cup B\text{.}$ Si$C$ es algún otro conjunto que contiene ambos$A$ y$B\text{,}$ luego $C$debe contener$A \cup B\text{;}$ por lo tanto,$A \cup B$ es el límite superior mínimo de$A$ y$B\text{.}$ De manera similar, el mayor límite inferior de$A$ y$B$ es$A \cap B\text{.}$

Ejemplo$19.11$

Dejemos$G$ ser un grupo y supongamos que ese$X$ es el conjunto de subgrupos de$G\text{.}$ Entonces

Solución

$X$es un poset ordenado por inclusión teórica de conjuntos,$\subset\text{.}$ El conjunto de subgrupos de$G$ es también una celosía. Si$H$ y$K$ son subgrupos$G\text{,}$ del mayor límite inferior de$H$ y$K$ es$H \cap K\text{.}$ El conjunto$H \cup K$ puede no ser un subgrupo de$G\text{.}$ Lo dejamos como un ejercicio para demostrar que el límite menor superior de$H$ y$K$ es el subgrupo generado por $H \cup K\text{.}$

En la teoría de conjuntos tenemos ciertas condiciones de dualidad. Por ejemplo, según las leyes de De Morgan, cualquier afirmación sobre conjuntos que sea cierta también$(A \cup B)'$ debe ser cierta sobre$A' \cap B'\text{.}$ Nosotros también tenemos un principio de dualidad para celosías.

Axioma$19.12$. Principle of Duality

Cualquier afirmación que sea verdadera para todas las celosías permanece verdadera cuando$\preceq$ es reemplazada por$\succeq$ y$\vee$ y$\wedge$ se intercambian a lo largo de la declaración

El siguiente teorema nos dice que una celosía es una estructura algebraica con dos operaciones binarias que satisfacen ciertos axiomas.

Teorema$19.13$

Si$L$ es una celosía, entonces las operaciones binarias$\vee$ y$\wedge$ satisfacer las siguientes propiedades para$a, b, c \in L\text{.}$

Leyes conmutativas:$a \vee b = b \vee a$ y$a \wedge b = b \wedge a\text{.}$
Leyes asociativas:$a \vee ( b \vee c) = (a \vee b) \vee c$ y$a \wedge (b \wedge c) = (a \wedge b) \wedge c\text{.}$
Leyes idempotentes:$a \vee a = a$ y$a \wedge a = a\text{.}$
Leyes de absorción:$a \vee (a \wedge b) = a$ y$a \wedge ( a \vee b ) =a\text{.}$

Prueba

Por el Principio de Dualidad, sólo necesitamos probar la primera afirmación en cada parte.

(1) Por definición$a \vee b$ es el límite inferior superior de$\{ a, b\}\text{,}$ y$b \vee a$ es el límite inferior superior de$\{ b, a \}\text{;}$ sin embargo,$\{ a, b\} = \{ b, a \}\text{.}$

(2) Vamos a demostrar que$a \vee ( b \vee c)$ y ambos$(a \vee b) \vee c$ son menos límites superiores de$\{ a, b, c \}\text{.}$ Let$d = a \vee b\text{.}$ Then$c \preceq d \vee c = (a \vee b) \vee c\text{.}$ We also know that

\[ a \preceq a \vee b =d \preceq d \vee c = (a \vee b) \vee c\text{.} \nonumber \]

Un argumento similar demuestra que$b \preceq (a \vee b) \vee c\text{.}$ Por lo tanto,$(a \vee b) \vee c$ es un límite superior de Ahora$\{ a, b, c \}\text{.}$ necesitamos mostrar que$(a \vee b) \vee c$ es el límite inferior superior de$\{ a, b, c\}\text{.}$ Let$u$ be algún otro límite superior de$\{ a, b, c \}\text{.}$ Entonces$a \preceq u$ y$b \preceq u\text{;}$ por lo tanto,$d = a \vee b \preceq u\text{.}$ Ya que$c \preceq u\text{,}$ sigue que$(a \vee b) \vee c = d \vee c \preceq u\text{.}$ Por lo tanto,$(a \vee b) \vee c$ debe ser el límite inferior superior de$\{ a, b, c\}\text{.}$ El argumento que muestra$a \vee ( b \vee c)$ es el límite inferior superior de$\{ a, b, c \}$ es el mismo. En consecuencia,$a \vee ( b \vee c) = (a \vee b) \vee c\text{.}$

3) La unión de$a$ y$a$ es el límite inferior superior de$\{ a \}\text{;}$ ahí,$a \vee a = a\text{.}$

(4) Que$d = a \wedge b\text{.}$ Entonces$a \preceq a \vee d\text{.}$ Por otro lado,$d = a \wedge b \preceq a\text{,}$ y así$a \vee d \preceq a\text{.}$ Por lo tanto,$a \vee ( a \wedge b) = a\text{.}$

Dado cualquier conjunto arbitrario$L$ con operaciones$\vee$ y$\wedge\text{,}$ satisfaciendo las condiciones del teorema anterior, es natural preguntarse si este conjunto proviene o no de alguna celosía. El siguiente teorema dice que este es siempre el caso.

Teorema$19.14$

$L$Sea un conjunto no vacío con dos operaciones binarias$\vee$ y que$\wedge$ satisfaga las leyes conmutativa, asociativa, idempotente y de absorción. Podemos definir un orden parcial en$L$ por$a \preceq b$ si$a \vee b = b\text{.}$ Además,$L$ es una celosía con respecto a$\preceq$ si para todos$a, b \in L\text{,}$ definimos el límite menor superior y el límite inferior más grande de$a$ y$b$ por$a \vee b$ y$a \wedge b\text{,}$ respectivamente.

Prueba

Primero mostramos que$L$ es un poset bajo$\preceq\text{.}$ Since$a \vee a = a\text{,}$$a \preceq a$ y$\preceq$ es reflexivo. Para demostrar que$\preceq$ es antisimétrico, dejar$a \preceq b$ y$b \preceq a\text{.}$ Entonces$a \vee b = b$ y$b \vee a = a\text{.}$ Por la ley conmutativa,$b = a \vee b = b \vee a = a\text{.}$ Finalmente, debemos demostrar que$\preceq$ es transitivo. Deja$a \preceq b$ y$b \preceq c\text{.}$ Entonces$a \vee b = b$ y$b \vee c = c\text{.}$ Así,

\[ a \vee c = a \vee (b \vee c ) = ( a \vee b) \vee c = b \vee c = c\text{,} \nonumber \]

o$a \preceq c\text{.}$

Para demostrar que$L$ es una celosía, debemos demostrar que$a \vee b$ y$a \wedge b$ son, respectivamente, los límites inferiores menos superiores y mayores de$a$ y$b\text{.}$ Ya que de$a=(a \vee b) \wedge a = a \wedge (a \vee b)\text{,}$ ello se deduce que$a \preceq a \vee b\text{.}$ De igual manera,$b \preceq a \vee b\text{.}$ Por lo tanto,$a \vee b$ es un límite superior para$a$ y $b\text{.}$$u$Sea cualquier otro límite superior de ambos$a$ y$b\text{.}$ Entonces$a \preceq u$ y$b \preceq u\text{.}$ Pero$a \vee b \preceq u$ desde

\[ (a \vee b) \vee u = a \vee (b \vee u) = a \vee u = u\text{.} \nonumber \]

La prueba de que$a \wedge b$ es el mayor límite inferior de$a$ y$b$ se deja como ejercicio.