9.1: El primer teorema del isomorfismo

Un teorema muy poderoso, llamado el Primer Teorema del Isomorfismo, nos permite en muchos casos identificar grupos factoriales (hasta isomorfismo) de una manera muy resbaladiza. Los granos jugarán un papel sumamente importante en esto. Por lo tanto, primero proporcionamos algunos teoremas relacionados con los granos.

Teorema\(\PageIndex{1}\)

Dejar\(G\) y\(G'\) ser grupos, dejar\(\phi\) ser un homomorfismo de\(G\) a\(G'\text{,}\) y dejar\(K=\text{Ker}\; \phi\text{.}\) Entonces por\(a,b\in G\text{,}\)\(aK=bK\) si y solo si\(\phi(a)=\phi(b)\text{.}\)

Prueba

Vamos\(a,b∈G\). Entonces

\( \begin{array} &ϕ(a)=ϕ(b)&⇔ϕ(b)^{−1}ϕ(a)=e_{G′}\\&⇔ϕ(b^{−1}a)=e_{G′}\\&⇔b^{−1}a∈K\\&⇔a∈bK\\&⇔aK=bK, \end{array}\)

según se desee.

Corolario\(\PageIndex{1}\)

Dejar\(\phi\) ser un homomorfismo de grupo\(G\) a grupo\(G'\text{.}\) Entonces\(\phi\) es uno a uno (de ahí un monomorfismo) si y solo si\(\text{Ker} \phi=\{e_G\}\text{.}\)

Prueba

Claramente, si\(ϕ\) es uno a uno entonces\(\text{Ker}⁡ϕ=\{e_G\}\). Por el contrario, supongamos\(\text{Ker}ϕ=\{e_G\}\).

Si\(a,b∈G\) con\(ϕ(a)=ϕ(b)\), entonces por el teorema anterior,\(a\text{Ker}⁡ϕ=b\text{Ker}⁡ϕ\). Pero\(a\text{Ker}⁡ϕ=a\{e_G\}=\{a\}\) y\(b\text{Ker}⁡ϕ=b\{e_G\}=\{b\}\). Así,\(a=b\), y vemos que\(ϕ\) es uno a uno.

Claramente, si\(\phi\) es uno a uno entonces\(\Ker \phi=\{e_G\}\text{.}\) Por el contrario, supongamos\(\Ker \phi=\{e_G\}\text{.}\) Si\(a,b\in G\) con\(\phi(a)=\phi(b)\text{,}\) entonces por el teorema anterior,\(a\Ker \phi=b\Ker \phi\text{.}\) Pero\(a\Ker \phi=a\{e_G\}=\{a\}\)\(a=b\text{,}\) y\(b\Ker \phi=b\{e_G\}=\{b\}\text{.}\) Así, y vemos que\(\phi\) es uno a uno.

Ahora demostramos un teorema que proporciona la carne y las papas del Teorema del Primer Isomorfismo.

Teorema\(\PageIndex{2}\): Factorization Theorem

Let\(G\) and\(G'\) be groups, let\(\phi\) be a homomorfism from\(G\) to\(G'\text{,}\)\(K=\text{Ker} \phi\text{,}\) let\(N\) be a normal subgroup of\(G\) with\(N\subseteq K\text{,}\) and let\(\Psi\) be the canonic epimorfism from\(G\) to\(G/N\text{.}\) then the map\(\overline{\phi}: G/N \to G'\) defined by \(\overline{\phi}(aN)=\phi(a)\)es un homomorfismo bien definido, con\(\overline{\phi} \circ \Psi=\phi\text{.}\)

Resumimos esto en la siguiente imagen:

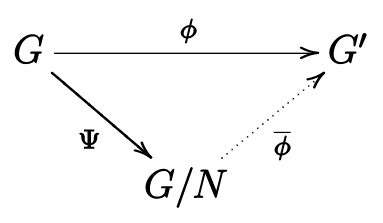
Prueba

Definimos\(\overline{\phi}:G/N→G′\), como se indicó anteriormente, por\(\overline{\phi}(aN)=ϕ(a)\) para cada\(aN∈G/N\). Ya que\(\overline{\phi}\) se define usando representantes de coset, primero debemos mostrar que\(\overline{\phi}\) está bien definido. Así que vamos\(aN=bN∈G/N\). Entonces\(\overline{\phi}(aN)=ϕ(a)\) y\(\overline{\phi}(bN)=ϕ(b)\), entonces debemos demostrarlo\(ϕ(a)=ϕ(b)\). Desde\(aN=bN\) y\(N⊆K\), tenemos eso\(aK=bK\) por Declaración 6 del Teorema\(7.2.3\); así\(ϕ(a)=ϕ(b)\) (usando Teorema\(9.1.1\)). Así\(\overline{\phi}\) está bien definido.

A continuación, mostramos que\(\overline{\phi}\) es un homomorfismo. Deja que un\(aN,bN∈G/N\). Entonces

\(\overline{\phi}((aN)(bN))= \overline{\phi}(abN)=ϕ(ab)=ϕ(a)ϕ(b)=\overline{\phi}(aN)\overline{\phi}(bN)\).

Por último, para cada\(a∈G\),

\((\overline{\phi} \circ Ψ)(a)=\overline{\phi}(Ψ(a))=\overline{\phi}(aN)=ϕ(a)\);

así\(\overline{\phi} \circ Ψ=ϕ\), según se desee.

Tenga en cuenta que el teorema anterior no establece que\(\overline{\phi}\) is a monomorphism or an epimorphism. This is because in general it may be neither! We do have the following theorem:

Teorema\(\PageIndex{3}\)

Dejar\(G\text{,}\)\(G'\text{,}\)\(\phi\text{,}\)\(N\text{,}\) y\(\overline{\phi}\) ser como se define en el Teorema de Factorización. Entonces

1. \(\overline{\phi}\)está en (un epimorfismo) si y solo si\(\phi\) está en (un epimorfismo); y
2. \(\overline{\phi}\)es uno a uno (un monomorfismo) si y solo si\(N=\text{Ker} \phi\text{.}\)

Prueba

Esto es claro, ya que\(\overline{\phi}(G/N)=ϕ(G)\).

Por Corolario\(9.1.1\),\(\overline{\phi}\) es uno a uno si y solo si\(\text{Ker}\overline{\phi}=\{N\}\). Pero

\(\begin{array}& \text{Ker}\overline{\phi}&=\{aN∈G/N:\overline{\phi}(aN)=e_{G′}\} \\&=\{aN∈G/N:ϕ(a)=e_{G′}\} \\&=\{aN∈G/N:a∈\text{Ker}ϕ\}. \end{array}\)

Así que\(\text{Ker}\overline{\phi}⁡=\{N\}\) si y solo si

\(\{aN∈G/N:a∈\text{Ker}ϕ\}=\{N\}\),

en otras palabras si y sólo si\(aN=N\) por todos\(a∈\text{Ker}⁡ϕ\). Pero

\(\begin{array} &&3&&aN=N   &\text{ for all } a∈\text{Ker}ϕ \\&& ⇔&a∈N   &\text{ for all } a∈\text{Ker}ϕ \\&&⇔&\text{Ker}ϕ⊆N \\&&⇔&\text{Ker}ϕ=N, \end{array}\)

ya que se nos da eso\(N⊆\text{Ker}⁡ϕ\). Así,\(\overline{\phi}\) es uno-a-uno si y sólo si\(N=\text{Ker}⁡ϕ\), según se desee.

Ahora estamos listos para exponer el importantísimo Teorema del Primer Isomorfismo, que se desprende directamente del Teorema y Teorema de Factorización\(9.1.3\).

Teorema\(\PageIndex{4}\): First Isomorphism Theorem

Dejar\(G\) y\(G'\) ser grupos, con homomorfismo\(\phi:G \rightarrow G'\text{.}\) Let\(K=\text{Ker} \phi\text{.}\)\(G/K \simeq \phi(G)\text{.}\) Then En particular, si\(\phi\) es on, entonces\(G/K\simeq G'\text{.}\)

Entonces para probar que un grupo factorial\(G/N\) es isomórfico a un grupo\(G'\text{,}\) basta con mostrar que existe un epimorfismo de\(G\) a\(G'\) que tiene\(N\) como núcleo.

Ejemplo\(\PageIndex{1}\)

\(n\in \mathbb{Z}^+\text{,}\)Dejemos que identifiquemos un grupo familiar al que\(GL(n,\mathbb{R})/SL(n,\mathbb{R})\) es isomórfico. Como en Ejemplo\(8.2.3\), el mapa\(\phi:GL(n,\mathbb{R})\to \mathbb{R}^*\) definido por\(\phi(A)\) es un homomorfismo con kernel\(SL(n,\mathbb{R})\text{.}\) Además,\(Phi\) claramente se mapea sobre\(\mathbb{R}^*\text{:}\) hecho, dada\(\lambda \in \mathbb{R}^*\text{,}\) la matriz diagonal que tiene\(\lambda\) en la posición más superior izquierda y\(1\) está en otra parte abajo la diagonal obtiene enviado a\(\lambda\) por\(\phi\text{.}\) Así por el Teorema del Primer Isomorfismo, tenemos\(GL(n,\mathbb{R})/SL(n,\mathbb{R}) \simeq \mathbb{R}^*\text{.}\)

Ejemplo\(\PageIndex{2}\)

Dejar\(G=S_3\times \mathbb{Z}_{52}\) y dejar\(N=S_3 \times \{0\}\subseteq G\text{.}\) Es sencillo demostrar que\(N\) es normal en\(G\text{.}\) Cuál es la estructura del\(G/N\text{?}\) Bien, definir\(\phi:G\to \mathbb{Z}_{52}\) por\(\phi((\sigma, a))=a\text{.}\) Entonces\(\phi\) es claramente un epimorfismo y\(\text{Ker} \phi=\{(\sigma,a)\in G\,:a=0\}=N\text{.}\) Así\(G/N\) es isomórfico a\(\mathbb{Z}_{52}\text{.}\)

Generalizando el ejemplo anterior, tenemos el siguiente teorema, cuya prueba dejamos al lector.

Teorema\(\PageIndex{5}\)

Let\(G=G_1\times G_2 \times \cdots \times G_k\) (where\(k\in \mathbb{Z}^+\)) y let\(N_i\) ser un subgrupo normal de\(G_i\) para cada\(i=1,2,\ldots, k\text{.}\) Entonces\(N=N_1 \times N_2 \times \cdots \times N_k\) es un subgrupo normal de\(G\text{,}\) con\(G/N \simeq G_1/N_1 \times G_2/N_2 \cdots \times G_k/N_k.\)

Brindamos un ejemplo más genial del uso del Teorema del Primer Isomorfismo. Claramente, ya que\(\mathbb{R}\) es abeliano,\(\mathbb{Z}\) es un subgrupo normal de\(\mathbb{R}\text{.}\) Cuál es la estructura del\(\mathbb{R}/\mathbb{Z}\text{?}\) Bien, en modding\(\mathbb{R}\) out by\(\mathbb{Z}\) hemos identificado esencialmente juntos todos los números reales que están separados a una distancia entera. ¡Entonces podemos pensar en el epimorfismo canónico de\(\mathbb{R}\) a\(\mathbb{R}/\mathbb{Z}\) como envolviéndolo\(\mathbb{R}\) como una manguera de jardín! Así, uno podría adivinar que\(\mathbb{R}/\mathbb{Z}\) tiene alguna estructura similar a un círculo, pero si queremos pensarlo como un grupo, ¡tenemos que averiguar cuál sería la estructura grupal en tal “círculo”!

Dejamos, por un momento, nuestro grupo\(\mathbb{R}/\mathbb{Z}\text{,}\) y miramos cómo podemos considerar que un círculo es un grupo.

Recordemos que para cada uno\(\theta \in \mathbb{R}\text{,}\)\(e^{i\theta}\) se define como\(\cos \theta + i\sin \theta\text{.}\) Es claro entonces que el conjunto\(S^1=\{e^{i\theta} \,:\, \theta\in \mathbb{R}\}\) es el círculo unitario en el plano complejo.

Obrar

Tenga en cuenta que si\(\theta_1, \theta_2\in \mathbb{R}\text{,}\) entonces\(e^{i\theta_1}=e^{i\theta_2}\) si y solo si\(\theta_1-\theta_2 \in 2\pi \mathbb{Z}\text{.}\)

Teorema\(\PageIndex{6}\)

\(S^1\)es un grupo bajo la multiplicación\(e^{i\theta_1}e^{i\theta_2}=e^{i(\theta_1+\theta_2)}\text{.}\)

Prueba

La parte complicada es demostrar que la operación está bien definida. Supongamos\(θ_1,θ_2,t_1\), y\(t_2\) están en\(R\), con\(e^{iθ_1}=e^{it_1}\) y\(e^{iθ_2}=e^{it_2}\). Queremos demostrar que

\(e^{iθ_1}e^{iθ_2}=e^{it_1}e^{it_2}\),

es decir, que

\(e^{i(θ_1+θ_2)}=e^{i(t_1+t_2)}\).

Ahora,\(e^{iθ_1}=e^{it_1}\) and \(e^{iθ_2}=e^{it_2}\) imply that \(θ_1−t_1=2πm\) and \(θ_2−t_2=2πn\) for some \(m\) a nd\(n\) in \(\mathbb{Z}\); hence,

\(θ_1+θ_2−(t_1+t_2)=2π(m+n)∈2π\mathbb{Z}\).

Por lo tanto,\(e^{i(θ_1+θ_2)}=e^{i(t_1+t_2)}\), so our operation is well-defined.

Dado que los productos de los elementos en\(S^1\) están en\(S^1\), tenemos que\(S^1\) es una estructura binaria; además, la asociatividad de la operación en se\(S^1\) desprende de la asociatividad de adición en\(\mathbb{R}\). Además,\(e^{i0}=1\) claramente actúa como un elemento de identidad en\(S^1\), y si\(e^{iθ}∈S^1\), entonces\(e^{iθ}\) tiene inversa\(e^{i(−θ)}∈S^1\). Así\(S^1\) es un grupo bajo la operación descrita.

La parte complicada es demostrar que la operación está bien definida. Supongamos\(\theta_1, \theta_2, t_1\text{,}\) and \(t_2\) are in \(\R\text{,}\) with \(e^{i\theta_1}=e^{it_1}\) and \(e^{i\theta_2}=e^{it_2}\text{.}\) We want to show that

\ begin {ecuación*} e^ {i\ theta_1} e^ {i\ theta_2} =e^ {it_1} e^ {it_2},\ end {ecuación*}

es decir, que

\ begin {ecuación*} e^ {i (\ theta_1+\ theta_2)} =e^ {i (t_1+t_2)}. \ end {ecuación*}

Ahora,\(e^{i\theta_1}=e^{it_1}\) and \(e^{i\theta_2}=e^{it_2}\) imply that \(\theta_1 -t_1 = 2\pi m\) and \(\theta_2-t_2 = 2\pi n\) for some \(m\) and \(n\) in \(\Z\text{;}\) hence,

\ begin {ecuación*}\ theta_1+\ theta_2- (t_1+t_2) = 2\ pi (m+n)\ in 2\ pi\ Z.\ end {ecuación*}

Por lo tanto,\(e^{i(\theta_1+\theta_2)}=e^{i(t_1+t_2)}\text{,}\) so our operation is well-defined.

Dado que los productos de los elementos en\(S^1\) are in \(S^1\text{,}\) we have that \(S^1\) is a binary structure; moreover, associativity of the operation in \(S^1\) follows from the associativity of addition in \(\R\text{.}\) Moreover, \(e^{i0}=1\) clearly acts as an identity element in \(S^1\text{,}\) and if \(e^{i\theta}\in S^1\text{,}\) then \(e^{i\theta}\) has inverse \(e^{i(-\theta)} \in S^1\text{.}\) So \(S^1\) is a group under the described operation.

Bellamente, resulta que nuestro grupo\(\mathbb{R}/\mathbb{Z}\) es isomórfico para\(S^1\text{.}\)

Teorema\(\PageIndex{7}\)

\(\mathbb{R}/\mathbb{Z} \simeq S^1\text{.}\)

Prueba

Vamos a definir un epimorfismo\(ϕ\) de\(\mathbb{R}\) a\(S^1\) con\(\text{Ker}ϕ=\mathbb{Z}\); luego tendremos\(\mathbb{R}/\mathbb{Z}≃S^1\), por el Teorema del Primer Isomorfismo.

Definir\(ϕ:\mathbb{R}→S^1\) por\(ϕ(r)=e^{i2πr}\). Tenemos que\(ϕ\) es un homomorfismo, ya que para cada\(r,s∈\mathbb{R}\), tenemos

\(ϕ(r+s)=e^{i2π(r+s)}=e^{i2πr+i2πs}=e^{i2πr}e^{i2πs}=ϕ(r)ϕ(s)\).

Por otra parte,\(ϕ\) is clearly onto, since if \(e^{iθ}∈S^1\), then

\(e^{iθ}=e^{i2π(θ2π)}=ϕ(θ2π)\).

Por último,\(\text{Ker}⁡ϕ=\mathbb{Z}\): indeed,

\(\begin{array}& r∈\text{Ker}⁡ϕ&⇔ϕ(r)=1\\&⇔e^{i2πr}=1\\&⇔\cos⁡2πr+i\sin⁡2πr=1\\&⇔\cos⁡2πr=1 \text{ and } \sin⁡2πr=0\\&⇔r∈\mathbb{Z}. \end{array}\)

Por lo tanto,\(\text{Ker}⁡ϕ=\mathbb{Z}\), and hence \(\mathbb{R}/\mathbb{Z}≃S^1\), as desired.

Definiremos un epimorfismo\(\phi\) from \(\R\) to \(S^1\) with \(\Ker \phi=\Z\text{;}\) then we'll have \(\R/\Z \simeq S^1\text{,}\) by the First Isomorphism Theorem.

Definir\(\phi:\R \to S^1\) by \(\phi(r)=e^{i2\pi r}\text{.}\) We have that \(\phi\) is a homomorphism, since for every \(r,s\in \R\text{,}\) we have

\ begin {ecuación*}\ phi (r+s) =e^ {i2\ pi (r+s)} =e^ {i2\ pi r+i2\ pi s} =e^ {i2\ pi r} e^ {i2\ pi s} =\ phi (r)\ phi (s). \ end {ecuación*}

Por otra parte,\(\phi\) is clearly onto, since if \(e^{i\theta}\in S^1\text{,}\) then

\ begin {ecuación*} e^ {i\ theta} =e^ {i2\ pi\ izquierda (\ frac {\ theta} {2\ pi}\ derecha)} =\ phi\ izquierda (\ frac {\ theta} {2\ pi}\ derecha). \ end {ecuación*}

Por último,\(\Ker\phi=\Z\text{:}\) indeed,

\ begin {align*} r\ in\ Ker\ phi\ amp\ Leftrightarrow\ phi (r) =1\\\ amp\ amp\ Leftrightarrow e^ {i2\ pi r} =1\\ amp\ amp\ Leftrightarrow\ cos 2\ pi r + i\ sin 2\ pi r=1\\ amp\ amp\ Leftrightarrow\ cos 2\ pi r = 1\ text y {}\ sin 2\ pi r = 0\\\ amp\ Leftrightarrow r\ in\ Z.\ end {alinear*}

Por lo tanto,\(\Ker \phi = \Z\text{,}\) and hence \(\R/\Z\simeq S^1\text{,}\) as desired.