2.1: Un primer ejemplo
- Page ID
- 117795
Comencemos nuestro estudio desarrollando cierta intuición sobre qué son realmente los grupos. Para comenzar, exploraremos el juego Spinpossible, que solía estar disponible para dispositivos iOS y Android.* El juego se juega en un\(3\times 3\) tablero de fichas revueltas numeradas del 1 al 9, cada una de las cuales puede estar del lado derecho hacia arriba o al revés. El objetivo del juego es devolver el tablero a la configuración estándar donde las fichas se disponen en orden numérico y del lado derecho hacia arriba. Esto se logra mediante una secuencia de “giros”, donde un giro consiste en rotar un\(m\times n\) subrectángulo 180\(^\circ\). El objetivo es minimizar el número de giros utilizados. La siguiente figura representa un tablero revuelto a la izquierda y el tablero resuelto a la derecha. La secuencia de flechas se utiliza para denotar alguna secuencia de giros que transforma el tablero revuelto en el tablero resuelto.
* Si quieres jugar el juego, intenta ir aquí: https://www.kongregate.com/games/spinpossible. ↩
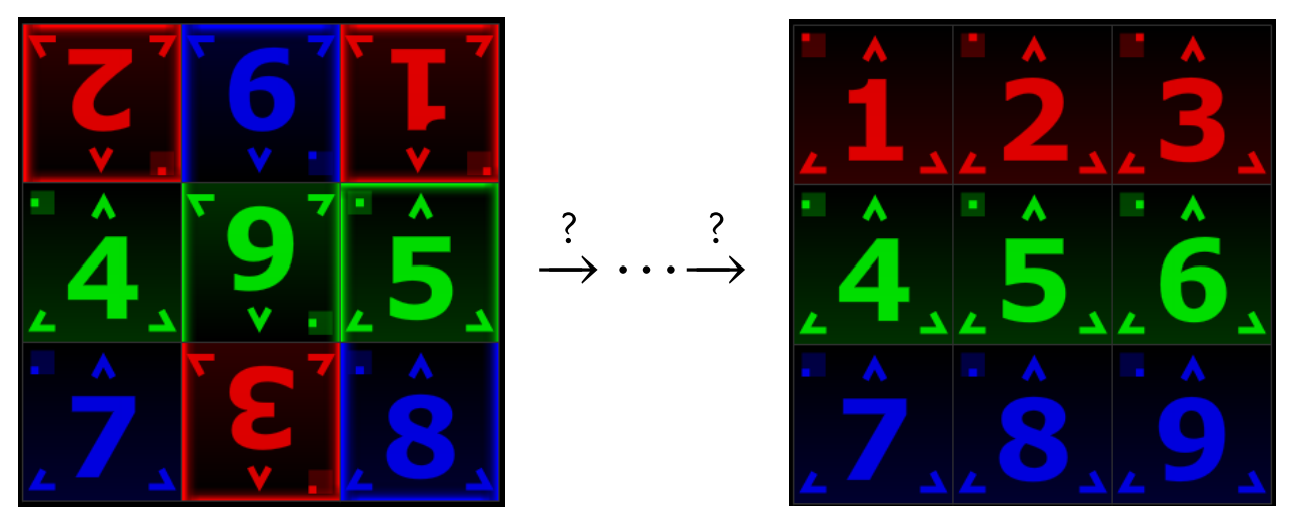
Juguemos con un ejemplo. Supongamos que comenzamos con el siguiente tablero revuelto.
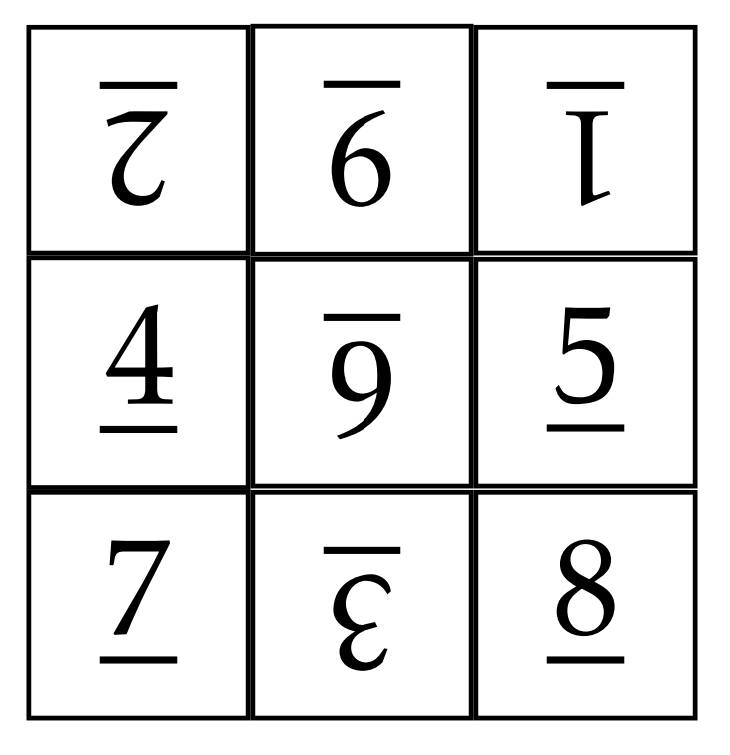
Los subrayados en los números están destinados a ayudarnos a saber si una ficha está del lado derecho hacia arriba o al revés. Nuestro objetivo es usar una secuencia de giros para descifrar el tablero. Antes de comenzar, pongamos de acuerdo en algunas convenciones. Cuando nos referimos a mosaico \(n\), nos referimos a la baldosa real que está etiquetada por el número\(n\) independientemente de su posición y orientación en el tablero. Por otro lado, la posición \(n\)se referirá a la posición en la placa en la que\(n\) se supone que debe estar la baldosa cuando la placa ha sido descifrada. Por ejemplo, en la tabla anterior, la loseta 1 está en la posición 3 y la loseta 7 pasa a estar en la posición 7.
Resulta que hay múltiples formas de descifrarlo, pero tengo una secuencia en particular en mente. Primero, hagamos girar el rectángulo determinado por las dos columnas más a la derecha. Esto es lo que obtenemos. He sombreado el subrectángulo que estamos girando.
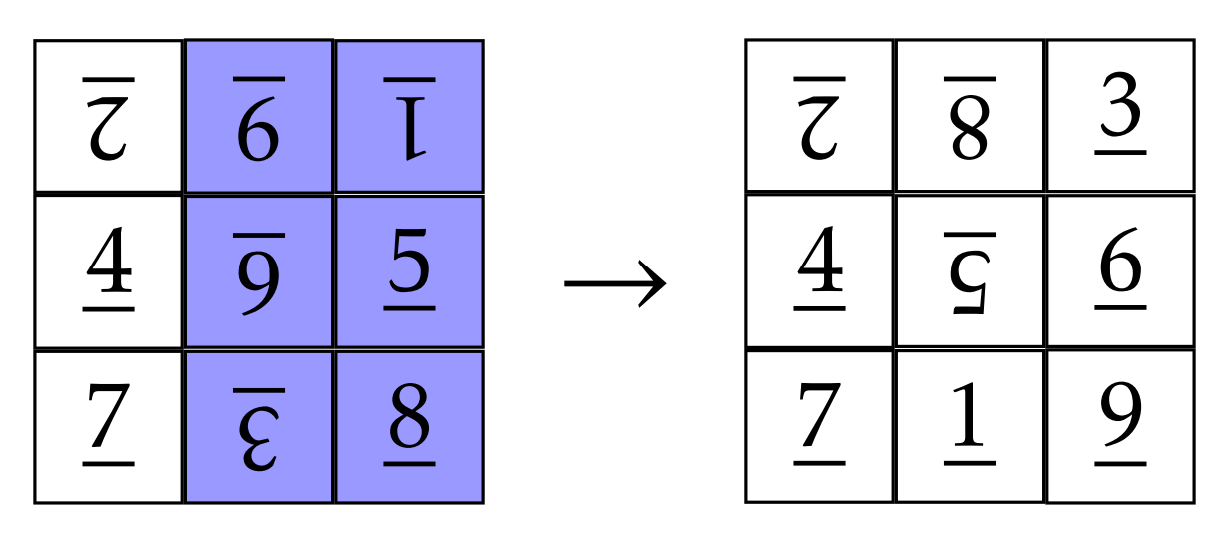
Bien, ahora vamos a girar la columna del medio.
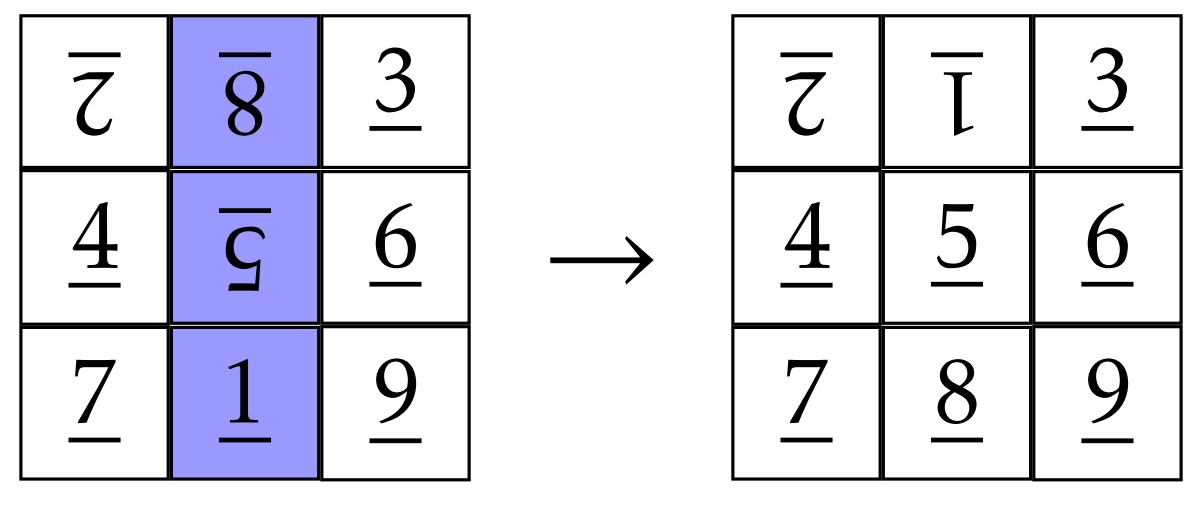
Ojalá puedan ver que estamos muy cerca de descifrar el tablero. Todo lo que tenemos que hacer es girar el rectángulo determinado por las fichas en las posiciones 1 y 2.
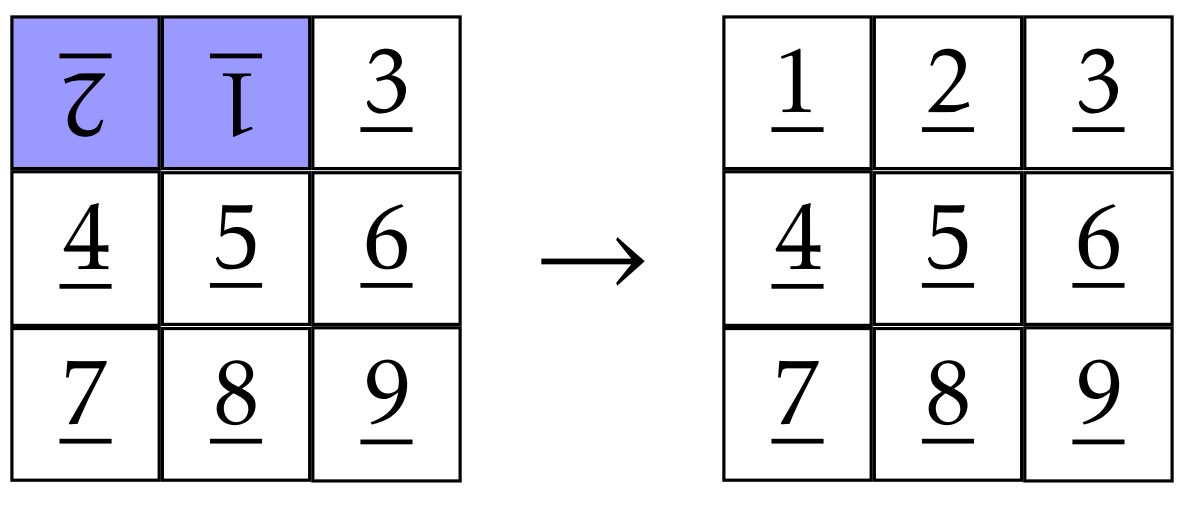
Armando todos nuestros movimientos, esto es lo que tenemos.

En este caso, pudimos resolver el tablero revuelto en 3 movimientos. No es inmediatamente obvio, pero resulta que no hay forma de descifrar el tablero en menos de 3 giros. Sin embargo, hay al menos otra solución que involucra exactamente 3 giros.
[prob:number_spinpossible_boards] ¿Cuántos tableros de\(3\times 3\) Spinpossible revueltos hay? Para responder a esta pregunta, deberá confiar en algunos principios de conteo como los factoriales. En este contexto, queremos incluir el tablero resuelto como uno de los tableros revueltos, simplemente no está muy revuelto.
¿Cuántos giros hay?
Es útil tener alguna notación. Dejar\(s_{ij}\) denotar el giro que gira el subrectángulo que tiene posición\(i\) en la esquina superior izquierda y posición\(j\) en la esquina inferior derecha. A modo de ejemplo, la secuencia de giros que usamos anteriormente para descifrar nuestro tablero revuelto inicial es\[s_{29}\to s_{28} \to s_{12}.\] Como notaste en Problem\(\PageIndex{2}\), también podemos rotar una sola ficha. Cada giro de la forma\(s_{ii}\) se llama toggle. Por ejemplo,\(s_{44}\) alterna la tesela en la posición 4.
Podemos pensar en cada giro como una función y como estamos haciendo giros encima de los giros, cada secuencia de giros corresponde a una composición de funciones. Seguiremos la convención estándar de composición de funciones que dice que la función de la derecha va primero. En este caso, nuestra secuencia anterior de giros se convierte\(s_{12} \circ s_{28} \circ s_{29}\), que abreviamos como\(s_{12} s_{28} s_{29}\). Esto podría llevar un poco acostumbrarse, pero solo recuerde que es como la notación de funciones: las cosas de la derecha van primero. Nos referiremos a expresiones\(s_{12} s_{28} s_{29}\) como palabras en el alfabeto\(\{s_{ij}\mid i\text{ upper left corner}, j\text{ lower right corner of subrectangle}\}\). Nuestras palabras siempre consistirán en un número finito de giros.
Cada palabra que consiste en giros corresponde a una función que toma un tablero revuelto como entrada y devuelve un tablero revuelto. Decimos que las palabras “actúan sobre” los tableros revueltos. Para cada palabra, hay una acción neta asociada. Por ejemplo, la palabra\(s_{12} s_{23} s_{12}\) corresponde al intercambio de las posiciones pero no a la orientación de los mosaicos en las posiciones 1 y 3. Deberías tomarte el tiempo para verificar esto por ti mismo. Observe que la acción neta no depende de la configuración actual de la placa. A veces es difícil describir cuál es la acción neta asociada a una palabra, pero siempre hay alguna acción neta correspondiente, no obstante. Además, cada acción neta tiene muchas—infinitamente muchas, de hecho— palabras que determinan esa acción neta. Por ejemplo, resulta que\(s_{12}s_{23}s_{12}\),\(s_{23}s_{12}s_{23}\), y\(s_{12}s_{23}s_{11}s_{11}s_{12}\) todos ceden la misma acción neta. En este caso, escribiríamos\[s_{12}s_{23}s_{12}=s_{23}s_{12}s_{23}=s_{12}s_{23}s_{11}s_{11}s_{12}.\] Aviso que la igualdad aquí se refiere a la acción neta y no a las propias palabras. Es decir, las palabras son diferentes, pero el resultado es el mismo.
Vale la pena señalar que no\(s_{12} s_{23} s_{12}\) es en sí mismo un giro. Sin embargo, a veces una composición de giros dará un giro. Por ejemplo, la acción neta de\(s_{12} s_{11} s_{12}\) es alternar el mosaico en la posición 2. Es decir,\(s_{12} s_{11} s_{12}=s_{22}\).
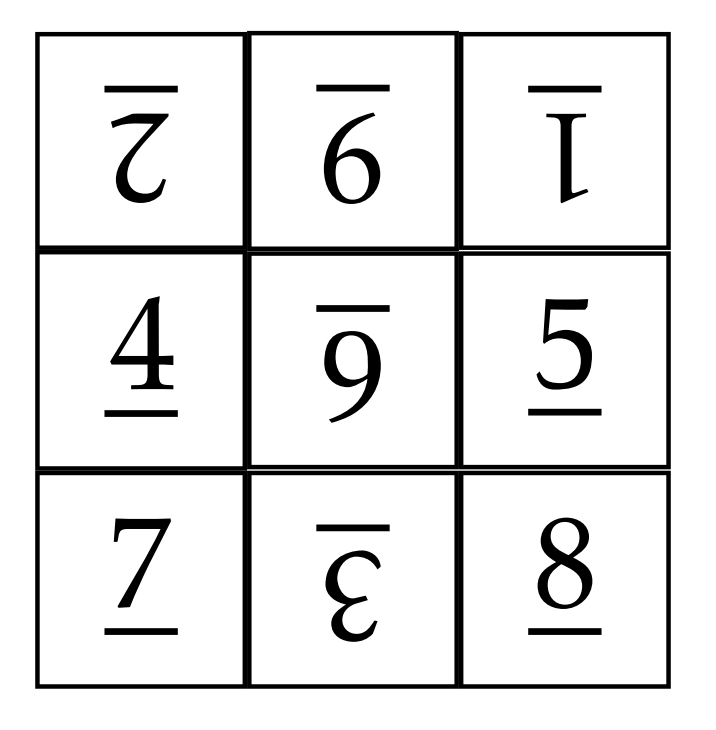
Encuentra una secuencia de 3 giros que sea diferente a la que describimos anteriormente que descifra la siguiente tabla. Escribe tu respuesta como una palabra que consiste en giros.
¿Cuál es la acción neta que corresponde a la palabra\(s_{23} s_{12} s_{23}\)? ¿De qué se puede concluir\(s_{23} s_{12} s_{23}\) en comparación con\(s_{12} s_{23} s_{12}\)?
También podemos usar exponentes para abreviar. Por ejemplo,\(s_{23}^2\) es lo mismo que\(s_{23} s_{23}\) (que en este caso es la acción neta de no hacer nada) y\((s_{12} s_{23})^2\) es lo mismo que\(s_{12} s_{23} s_{12} s_{23}\).
Resulta que hay una palabra aún más simple (es decir, una palabra más corta) que produce la misma acción neta que\((s_{12} s_{23})^2\). ¿Puedes encontrar uno?
\(\text{Spin}_{3\times 3}\)Definir como la colección de acciones netas que podemos obtener de palabras consistentes en giros. Decimos que el conjunto de giros genera\(\text{Spin}_{3\times 3}\) y nos referimos al conjunto de giros como un conjunto generador para\(\text{Spin}_{3\times 3}\).
Supongamos\(s_{x_1}s_{x_2}\cdots s_{x_n}\) y\(s_{y_1}s_{y_2}\cdots s_{y_m}\) son ambas palabras que consisten en giros. Entonces las acciones netas correspondientes, digamos\(u\) y\(v\), respectivamente, son elementos de\(\text{Spin}_{3\times 3}\). Demostrar que la composición de las acciones\(u\) y\(v\) es un elemento de\(\text{Spin}_{3\times 3}\).
El problema anterior nos dice que la composición de dos acciones netas a partir de\(\text{Spin}_{3\times 3}\) los resultados en otra acción neta en\(\text{Spin}_{3\times 3}\). Formalmente, decimos que\(\text{Spin}_{3\times 3}\) está cerrado bajo composición.
Es claro que podemos construir un número infinito de palabras consistentes en giros, pero como hay un número finito de formas de reorganizar las posiciones y orientaciones de los mosaicos del\(3\times 3\) tablero, solo hay un número finito de acciones netas que surgen de estas palabras. Es decir,\(\text{Spin}_{3\times 3}\) es un conjunto finito de funciones.
Verificar que\(\text{Spin}_{3\times 3}\) contiene una función de identidad, es decir, una función cuya acción neta es “no hacer nada”. ¿Qué pasa si componemos una acción neta a partir de\(\text{Spin}_{3\times 3}\) con la identidad?
Una pregunta natural es si todos los posibles tableros de Spinpossible revueltos pueden ser descifrados usando solo giros. En otras palabras, ¿es\(\text{Spin}_{3\times 3}\) suficiente para descifrar cada tablero revuelto? Resulta que la respuesta es sí.
Verifique que\(\text{Spin}_{3\times 3}\) sea suficiente para descifrar cada tablero cifrado describiendo un algoritmo que siempre descifrará un tablero cifrado. No importa si tu algoritmo es eficiente. Es decir, no nos importa cuántos pasos se necesitan para descifrar el tablero siempre y cuando funcione en un número finito de pasos. Usando tu algoritmo, ¿cuál es el número máximo de giros necesarios para descifrar cualquier tablero revuelto?
En un artículo de 2011, Alex Sutherland y Andrew Sutherland (un equipo de padre e hijo) presentan una serie de resultados interesantes sobre Spinpossible y enumeran algunos problemas abiertos. Puedes encontrar la ponencia en http://arxiv.org/abs/1110.6645. Como nota al margen, Alex es uno de los desarrolladores del juego y su padre, Andrew, es profesor de matemáticas en el MIT. Usando un algoritmo informático de fuerza bruta, los Suland verificaron que cada tablero de\(3\times 3\) Spinpossible revuelto se puede resolver como máximo en 9 movimientos. Sin embargo, una prueba matemática legible por humanos de este hecho sigue siendo esquiva. Por cierto, las matemáticas están repletas de problemas abiertos y a menudo se puede llegar a la frontera de lo que actualmente se conoce sin demasiados problemas. Los matemáticos están en el negocio de resolver problemas abiertos.
En lugar de desordenar tableros, podemos actuar sobre el tablero resuelto con una acción de\(\text{Spin}_{3\times 3}\) para obtener un tablero revuelto. El problema nos\(\PageIndex{8}\) dice que podemos usar\(\text{Spin}_{3\times 3}\) para pasar de la placa resuelta a cualquier tablero revuelto. De hecho, a partir de la placa resuelta deja claro que existe una correspondencia uno a uno entre las acciones netas y los tableros revueltos.
¿Cuál es el tamaño de\(\text{Spin}_{3\times 3}\)? Es decir, ¿en cuántas acciones netas hay\(\text{Spin}_{3\times 3}\)?
Hagamos un par de observaciones más. Primero, cada giro es reversible. Es decir, cada giro tiene una inversa. En el caso de Spinpossible, solo podemos aplicar el mismo giro nuevamente para deshacerlo. Por ejemplo,\(s_{12}^2\) es lo mismo que no hacer nada. Esto quiere decir que lo inverso de\(s_{12}\), denotado\(s_{12}^{-1}\), es\(s_{12}\) en sí mismo. Simbólicamente, escribimos\(s_{12}^{-1}=s_{12}\). Recuerda que estamos explorando el juego Spinpossible, no siempre será el caso de que repetir una acción revertirá la acción.
En la misma línea, cada secuencia de giros es reversible. Por ejemplo, si aplicamos\(s_{12} s_{23}\) (es decir, hacer\(s_{23}\) primero seguido de\(s_{12}\)), podríamos deshacer la acción neta aplicando\(s_{23} s_{12}\) porque\[(s_{12} s_{23})^{-1}=s_{23}^{-1} s_{12}^{-1}=s_{23} s_{12}\] since\(s_{23}^{-1}=s_{23}\) y\(s_{12}^{-1}=s_{12}\). Observe que la primera igualdad es una instanciación del “teorema de calcetines y zapatos”, que establece que si\(f\) y\(g\) son funciones con dominio y codominio compatibles, entonces\[(f\circ g)^{-1} = g^{-1}\circ f^{-1}.\] El resultado es que la acción neta que corresponde a una palabra que consiste en giros se puede revertir aplicando “calcetines y zapatos” y es en sí misma una acción.
Imagina que empezamos con el tablero resuelto y luego revolviste el tablero de acuerdo con alguna palabra que consiste en giros. Llamemos a esta palabra\(w\). ¿Cómo se podría obtener la placa resuelta del tablero revuelto determinado por\(w\)? ¿Cómo se relaciona esto\(w^{-1}\)?
Hay un detalle que hemos estado barriendo debajo de la alfombra. Observe que cada vez que escribimos una palabra que consistía en dos o más giros, no nos molestamos en agrupar pares de giros adyacentes usando paréntesis. Recordemos que la composición de funciones con dominios y codominios compatibles es asociativa (ver Teorema 2.2.1). Es decir, si\(f\),\(g\), y\(h\) son funciones con dominios y codominios compatibles, entonces\[(f\circ g)\circ h = f\circ (g\circ h).\] Dado que la composición de los giros es realmente solo composición de funciones, la composición de los giros también es asociativa. Y como los giros generan\(\text{Spin}_{3\times 3}\), la composición de las acciones netas a partir de\(\text{Spin}_{3\times 3}\) es asociativa, también.
¿Importa el orden en el que aplicas los giros? ¿Siempre importa? Seamos lo más específicos posible. Si el orden en el que aplicamos dos giros no importa, entonces decimos que los giros conmutan. Sin embargo, si el pedido sí importa, entonces los giros no se conmutan. ¿Cuándo viajarán dos giros? ¿Cuándo no viajarán? Proporcione algunos ejemplos específicos.
En el problema anterior, descubriste que la composición de dos giros puede o no conmutar. Dado que los giros se generan\(\text{Spin}_{3\times 3}\), la composición de dos acciones netas puede o no conmutar. Decimos que no\(\text{Spin}_{3\times 3}\) es conmutativo.
Recopilemos nuestras observaciones clave sobre\(\text{Spin}_{3\times 3}\).
- Grupo Generador: El conjunto de giros genera\(\text{Spin}_{3\times 3}\). Es decir, cada acción neta de\(\text{Spin}_{3\times 3}\) corresponde a una palabra que consiste en giros. 1
- Cierre: La composición de dos acciones netas cualesquiera a partir de\(\text{Spin}_{3\times 3}\) los resultados en una acción neta de\(\text{Spin}_{3\times 3}\).
- Asociativa: La composición de las acciones netas a partir de\(\text{Spin}_{3\times 3}\) es asociativa.
- Identidad: Hay una identidad en\(\text{Spin}_{3\times 3}\) cuya acción neta correspondiente es “no hacer nada”.
- Inversa: Cada acción neta de\(\text{Spin}_{3\times 3}\) tiene una acción neta inversa en\(\text{Spin}_{3\times 3}\). Componer una acción neta y sus resultados inversos en la identidad.
- La composición de dos acciones netas de\(\text{Spin}_{3\times 3}\) puede o no conmutar.
Resulta que\(\text{Spin}_{3\times 3}\) es un ejemplo de grupo. Hablando vagamente, un grupo es un conjunto junto con un método para combinar dos elementos juntos que satisface las condiciones (2), (3), (4) y (5) anteriores. De manera más formal, un grupo es un conjunto no vacío junto con una operación binaria asociativa tal que el conjunto contiene un elemento de identidad y cada elemento del conjunto tiene una inversa que también está en el conjunto. Como veremos, los grupos pueden tener una variedad de grupos generadores, posiblemente de diferentes tamaños. Además, algunos grupos son conmutativos y algunos grupos no lo son.
Antes de cerrar esta sección, abordemos algunos problemas más interesantes sobre Spinpossible. Decimos que un conjunto generador\(S\) para un grupo es un conjunto generador mínimo si ya no\(S\setminus\{x\}\) es un conjunto generador para el grupo para todos\(x\in S\).
Determine si el conjunto de giros es un conjunto generador mínimo para\(\text{Spin}_{3\times 3}\).
- *
-
El caso de Spinpossible es un poco engañoso. Dado que cada giro es su propio inverso, nunca necesitamos escribir palabras consistentes en giros con inversos. Sin embargo, como veremos más adelante, hay situaciones fuera del contexto de Spinpossible donde necesitaremos utilizar inversos de elementos de un conjunto generador.
No es demasiado difícil de probar, pero omitiremos los detalles, que podemos generar\(\text{Spin}_{3\times 3}\) con el siguiente subconjunto de 9 giros: Es\[T=\{s_{11}, s_{12}, s_{23}, s_{36}, s_{56}, s_{45}, s_{47}, s_{78}, s_{89}\}.\] decir, cada acción neta en\(\text{Spin}_{3\times 3}\) corresponde a una palabra que consiste en los giros de\(T\). Intenta tomarte un momento para convencerte de que esto es al menos plausible.
Para cada uno de los siguientes giros, encuentra una palabra que consiste en giros del conjunto\(T\) que produzca la misma acción neta.
- \(s_{33}\)
- \(s_{13}\)
- \(s_{14}\)
Dando por sentado que\(T\) es un grupo generador para\(\text{Spin}_{3\times 3}\), determinar si\(T\) es un conjunto generador mínimo.


