2.6: Diagramas Cayley
- Page ID
- 117785
En esta sección, introduciremos la forma visual de codificar la estructura abstracta del grupo en términos de un conjunto generador especificado. Para empezar, juguemos con un ejemplo.
Recordemos que en el Problema 2.1.1, descubrimos que hay un total de\(2^9\cdot 9! = 185,794,560\) posibles tableros\(3\times 3\) Spinpossible revueltos. Ahora, imagina que queríamos escribir un manual de soluciones que describiera cómo resolver todas estas placas. Hay muchas formas posibles de construir un manual de soluciones de este tipo, pero aquí hay una manera.
El manual constará de\(185,794,560\) páginas tales que cada página enumera una codificación única del\(3\times 3\) tablero. No olvides que uno de estos scramblings es el tablero resuelto, que haremos página 1. Además, imagina que el libro está arreglado de tal manera que no sea demasiado difícil buscar un tablero revuelto dado. En cada página debajo del tablero revuelto hay una tabla que enumera todos los giros posibles. Al lado de cada giro, la tabla indica si hacer ese giro en particular dará como resultado una tabla que esté más cerca de resolverse o más lejos de resolverse. Además, el número de página que corresponde al tablero resultante se enumera junto a cada giro.
En la mayoría de los casos, habrá muchos giros que nos acercan más al tablero resuelto. Dado un tablero revuelto, una solución consistiría en seguir una posible secuencia de páginas a través del libro que nos lleva del tablero revuelto al tablero resuelto. Podría haber muchas secuencias de este tipo. Si pudiéramos construir tal manual de solución, tendríamos un atlas o mapa para el juego Spinpossible.
Tenga en cuenta que incluso si hacemos un giro equivocado (es decir, seguimos una página que nos aleja más de la solución), aún podemos volver al camino siguiendo números de página que nos acercan más al tablero resuelto. De hecho, siempre podemos volver a la página en la que estábamos antes de dar un giro equivocado. Esta página aparecerá en nuestra “página de vuelta equivocada” ya que hacer el mismo giro dos veces tiene el efecto neto de no hacer nada. Si realmente hicieras esto, el número de páginas que necesitaríamos visitar sería más largo que una solución óptima, pero llegaríamos al tablero resuelto de todos modos.
Vamos a ponernos un poco más concretos. Considera el juego Spinpossible, excepto vamos a simplificarlo un poco. En lugar de jugar en el\(3\times 3\) tablero, juguemos en un\(1\times 2\) tablero que consiste en una sola fila con fichas etiquetadas 1 y 2. Las reglas del juego son lo que esperarías; estamos restringidos a giros que involucran solo las fichas en las posiciones 1 y 2 del tablero original. Una mezcla de la tabla\(1\times 2\) Spinpossible consiste en cualquier reordenamiento de las fichas 1 y 2, donde cualquiera de las fichas puede estar del lado derecho hacia arriba o al revés.
Dejar\(\text{Spin}_{1\times 2}\) denotar el grupo de acciones netas que corresponde a composiciones de giros permitidos en el tablero\(1\times 2\) Spinpossible.
- ¿Cuántos tableros revueltos hay para el juego\(1\times 2\) Spinpossible? Escríbelos todos. No olvides incluir la placa resuelta.
- ¿Cuál es el orden de\(\text{Spin}_{1\times 2}\)?
- Verifica eso\(\text{Spin}_{1\times 2}=\langle s_{11}, s_{22}, s_{12}\rangle\) escribiendo cada elemento como una palabra en\(s_{11}\),\(s_{22}\), o\(s_{12}\).
- ¿Es\(\{s_{11}, s_{22}, s_{12}\}\) un grupo electrógeno mínimo para\(\text{Spin}_{1\times 2}\)?
Intentemos hacer un mapa para\(\text{Spin}_{1\times 2}\), pero en lugar de escribir un manual de solución, dibujaremos un diagrama del grupo. Lo primero que haremos es dibujar cada uno de los scramblings que encontramos en el problema anterior. No importa cómo arreglemos todos estos dibujos, siempre y cuando haya algún espacio entre ellos. Ahora, para cada uno de nuestros 8 tableros revueltos, descubre qué sucede cuando hacemos cada uno de nuestros 3 giros permitidos. Para cada uno de estos giros, dibujaremos una flecha del tablero revuelto en consideración al tablero resultante. No te preocupes por si hacer cada uno de estos giros es una buena idea o no. En este caso, cada una de nuestras tablas revueltas tendrá 3 flechas que se dirigen hacia 3 tablas distintas. ¿Ves por qué?
Para que mantengamos recto lo que representa cada flecha, coloreemos nuestras flechas, para que hacer un tipo particular de giro sea siempre del mismo color. Por ejemplo, podríamos colorear las flechas que alternan el mosaico en la primera posición como verde. Recordemos que hacer el mismo giro dos veces tiene el efecto neto de no hacer nada, así que hagamos que todas nuestras flechas apunten en ambas direcciones.
Para asegurarte de que estás siguiendo, considera el siguiente tablero revuelto.
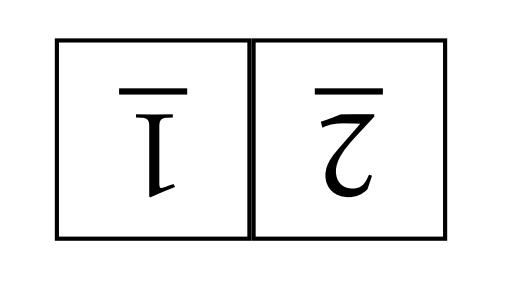
Este tablero es uno de nuestros 8 posibles\(1\times 2\) tableros revueltos. Tenemos tres posibles giros que podemos hacer a este tablero: alternar la posición 1, alternar la posición 2, o girar toda la tabla. Cada uno de estos giros tiene una flecha de dos vías correspondiente que nos lleva a tres tableros revueltos diferentes. La figura\(\PageIndex{2}\) proporciona una representación visual de lo que acabamos de discutir.
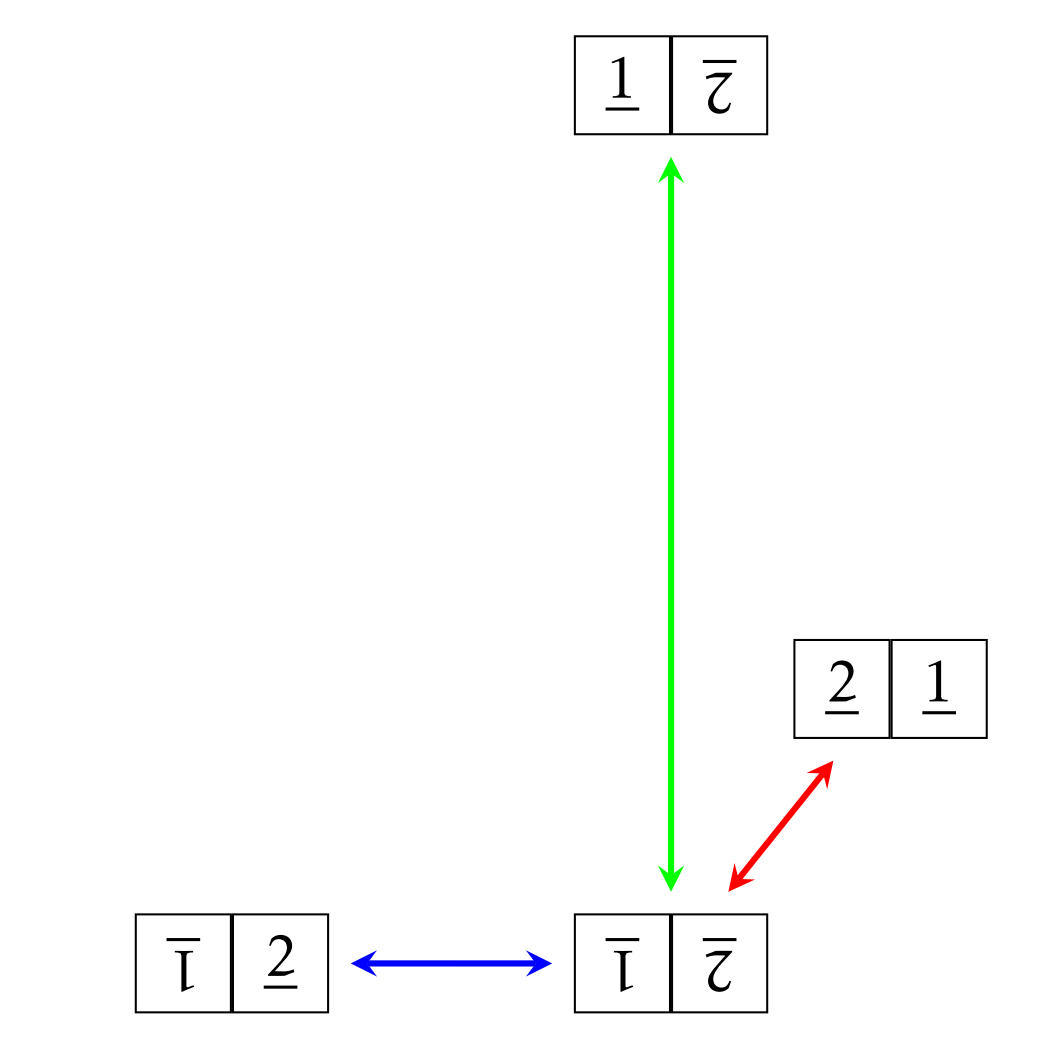
Tenga en cuenta que podría haber dibujado los cuatro tableros revueltos en Figura en\(\PageIndex{2}\) cualquier lugar que quisiera, pero tengo un diseño particular en mente. Además, fíjate que tenemos tres flechas de diferentes colores. En este caso, una flecha verde corresponde a alternar la baldosa en la posición 1 (\(s_{11}\)), una flecha azul corresponde a alternar la posición 2 (\(s_{22}\)), y una flecha roja corresponde a girar toda la tabla (\(s_{12}\)).
Si incluimos el resto de los tableros revueltos y todos los giros posibles, obtenemos Figura\(\PageIndex{3}\). Tenga en cuenta que he elegido un bonito diseño para la figura, pero realmente son las conexiones entre las distintas placas las que son importantes.
En definitiva, queremos un diagrama que transmita información sobre la estructura del grupo, así que en lugar de etiquetar los vértices del diagrama para\(\text{Spin}_{1\times 2}\) en Figura\(\PageIndex{3}\) con tableros revueltos, etiquetaremos los vértices con los elementos del grupo de una manera que respete la configuración de flechas. Pero para hacer esto, necesitamos tomar una decisión sobre cómo empezar a etiquetar. Una elección natural a hacer es etiquetar el tablero resuelto con la identidad\(e\). Entonces cada tablero revuelto debe ser etiquetado por el elemento de grupo que corresponde a la acción neta que nos lleva del tablero resuelto a ese tablero revuelto.
Una forma de hacerlo es etiquetar cada vértice con la palabra que corresponde a un camino de flechas que conduce al vértice desde el vértice etiquetado por la identidad\(e\). No te olvides
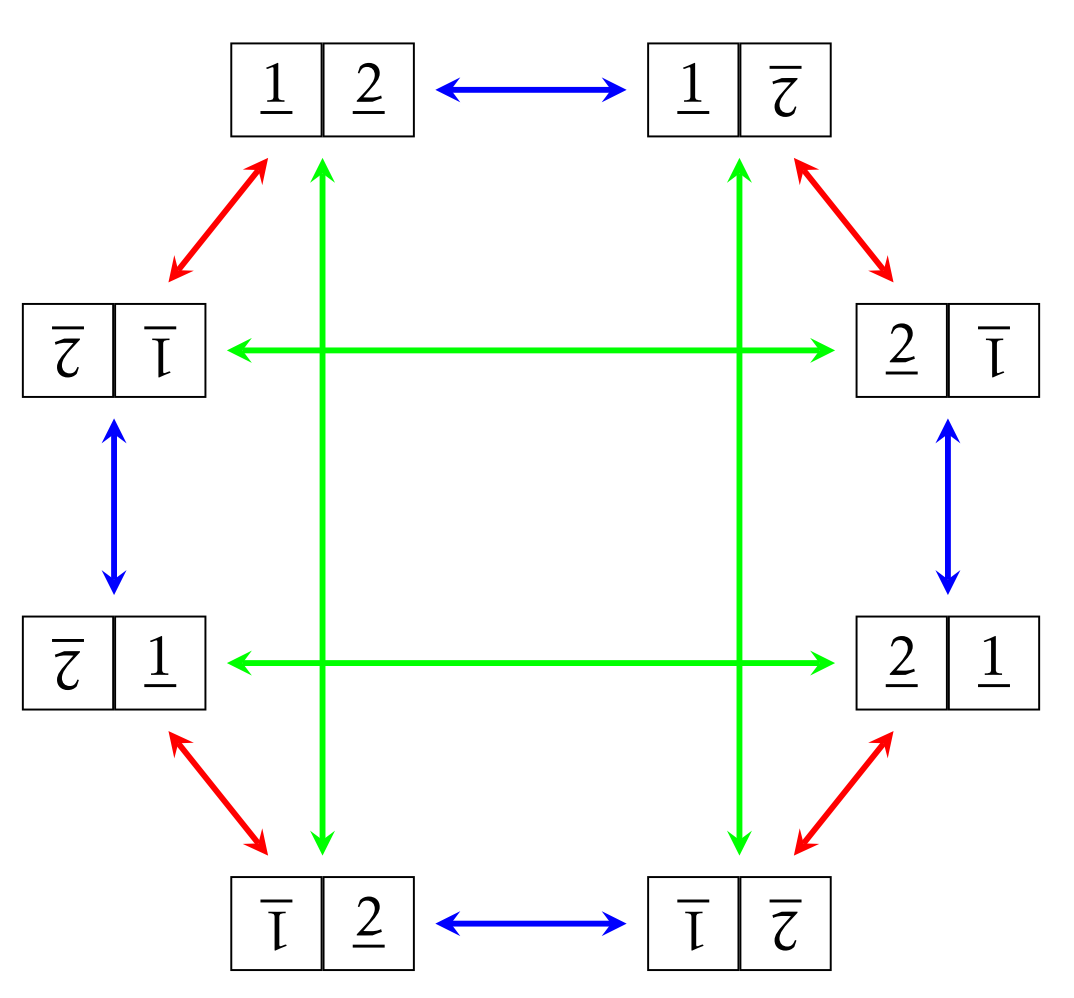
que aplicamos nuestra composición de acciones de derecha a izquierda. Esto significa que siguiendo una secuencia de flechas fuera del vértice etiquetado por\(e\) se grabará como una palabra escrita de derecha a izquierda. Es decir, la primera flecha de\(e\) corresponde a la letra más a la derecha de la palabra.
Por ejemplo, considere el siguiente tablero revuelto.
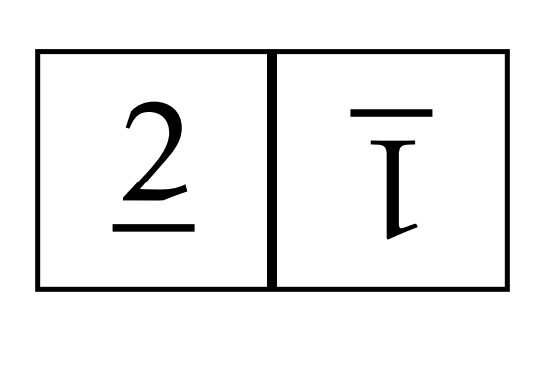
Al mirar Figura\(\PageIndex{3}\), vemos que una forma de llegar a este tablero desde el tablero resuelto es seguir una flecha azul y luego una flecha roja. Esto corresponde a la palabra\(s_{12}s_{22}\). Sin embargo, también corresponde a la palabra\(s_{22}s_{12}s_{22}s_{11}\) aunque esta no sea una solución óptima. Entonces, podemos etiquetar el tablero en cuestión con cualquiera\(s_{12}s_{22}\) o\(s_{22}s_{12}s_{22}s_{11}\) y hay otras opciones, también.
Usando Figura\(\PageIndex{3}\), encuentre tres palabras distintas en\(s_{11}, s_{22}\), o\(s_{12}\) que correspondan a la siguiente tabla replegada.
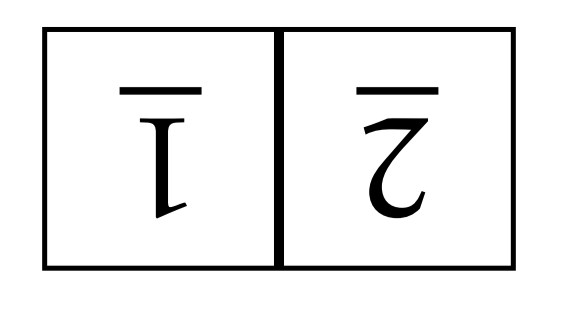
Si seguimos etiquetando los vértices de la gráfica dirigida en la Figura\(\PageIndex{3}\), entonces se da un posible etiquetado en la Figura\(\PageIndex{6}\). Cada palabra te dice cómo llegar al tablero revuelto correspondiente desde el tablero resuelto. El gráfico dirigido en la Figura\(\PageIndex{6}\) se llama el diagrama de Cayley para su\(\text{Spin}_{1\times 2}\) uso\(\{s_{11},s_{22},s_{12}\}\) como conjunto generador. Es importante señalar que no siempre se dará el caso de que las flechas sean flechas de dos vías. Esto pasó a ser el caso aquí porque cada uno de nuestros generadores es su propio inverso.
Considere el diagrama de Cayley para\(\text{Spin}_{1\times 2}\) en la Figura\(\PageIndex{6}\).
- Quitar todas las flechas rojas corresponde a prohibir el giro que gira la\(1\times 2\) pensión completa. ¿Podemos obtener todos los tableros revueltos del tablero resuelto usando solo flechas azules y verdes? ¿De qué te dice esto\(\{s_{11},s_{22}\}\)?
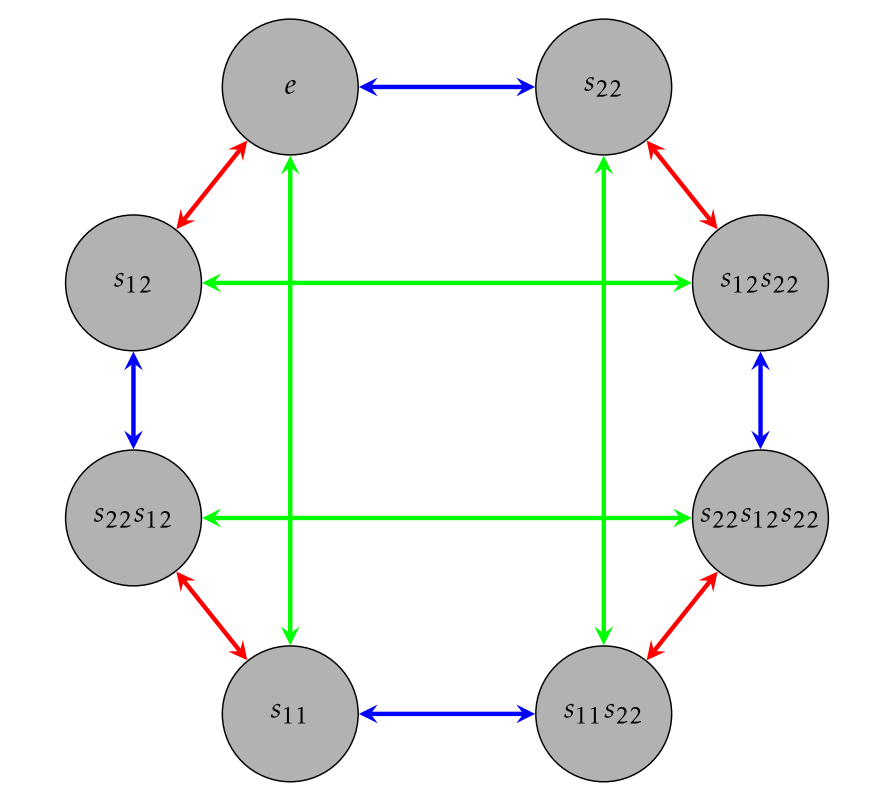
- ¿Y si quitamos las flechas azules? ¿De qué te dice esto\(\{s_{11},s_{12}\}\)?
- ¿Y si quitamos las flechas verdes? ¿De qué te dice esto\(\{s_{22},s_{12}\}\)?
Supongamos que\(G\) es un grupo y\(S\) es un conjunto generador de\(G\). El diagrama Cayley * para\(G\) con grupo generador\(S\) es un gráfico dirigido a color construido de la siguiente manera:
- Los vértices corresponden a elementos de\(G\).
- A cada generador\(s\in S\) se le asigna un color, digamos\(c_s\).
- Para\(g\in G\) y\(s\in S\), hay un borde dirigido de\(g\) a\(sg\) con color\(c_s\).
- *
-
Los diagramas de Cayley llevan el nombre de su inventor Arthur Cayley, un matemático británico del siglo XIX.
Tenga en cuenta que seguir la flecha de\(g\) a\(sg\) con color\(c_s\) corresponde a aplicar la acción de\(s\) a\(g\). Además, seguir la flecha hacia atrás de\(sg\) a\(g\) corresponde aplicar\(s^{-1}\) a\(sg\). Si un generador es su propio inverso (como los giros adentro\(\text{Spin}_{1\times 2}\)), entonces las flechas correspondientes a ese generador son flechas bidireccionales.
Antes de pedirte que construyas algunos diagramas de Cayley, juguemos con otro ejemplo. En el siguiente problema te encontrarás con un diagrama de Cayley donde todos los bordes son flechas unidireccionales.
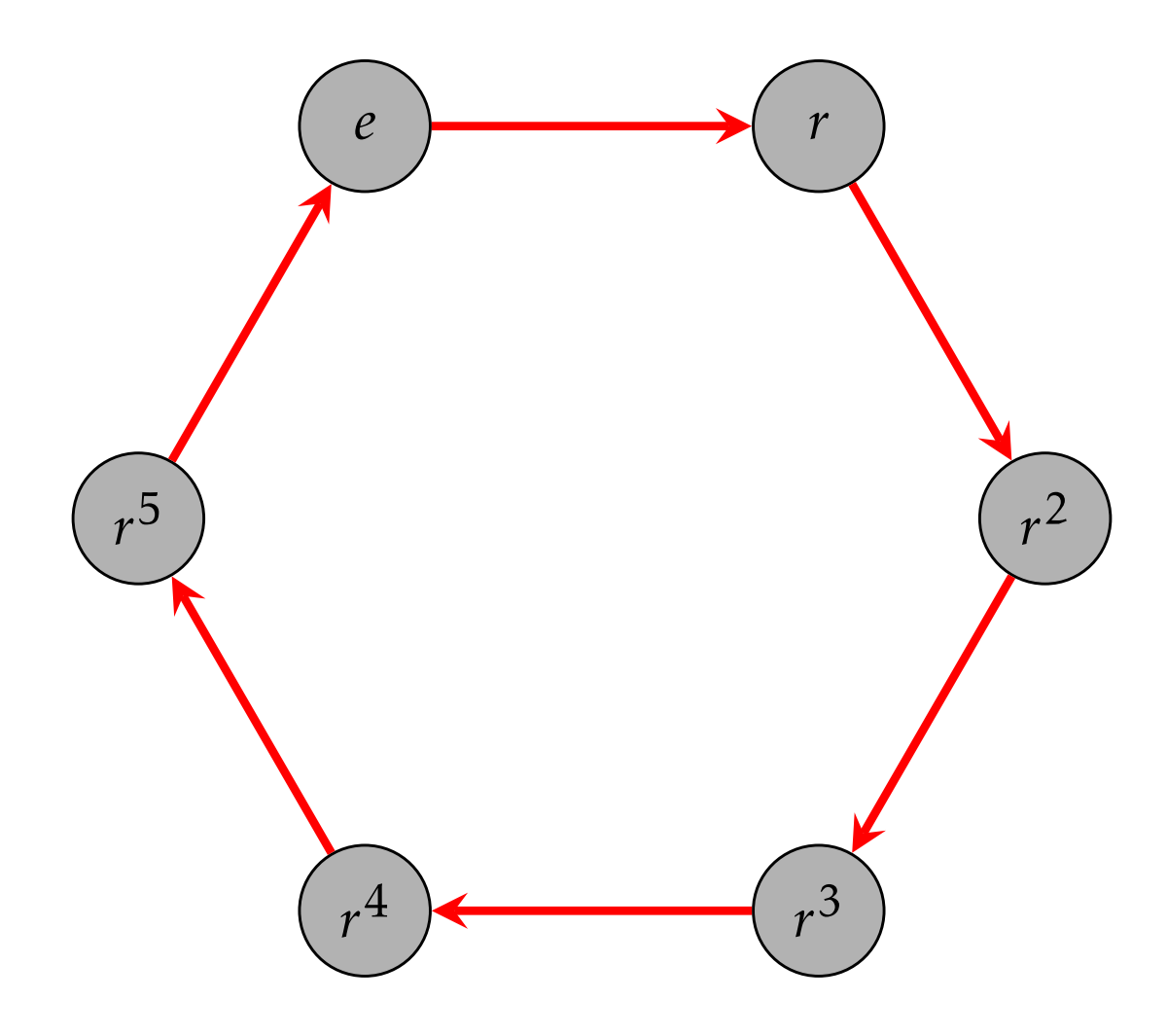
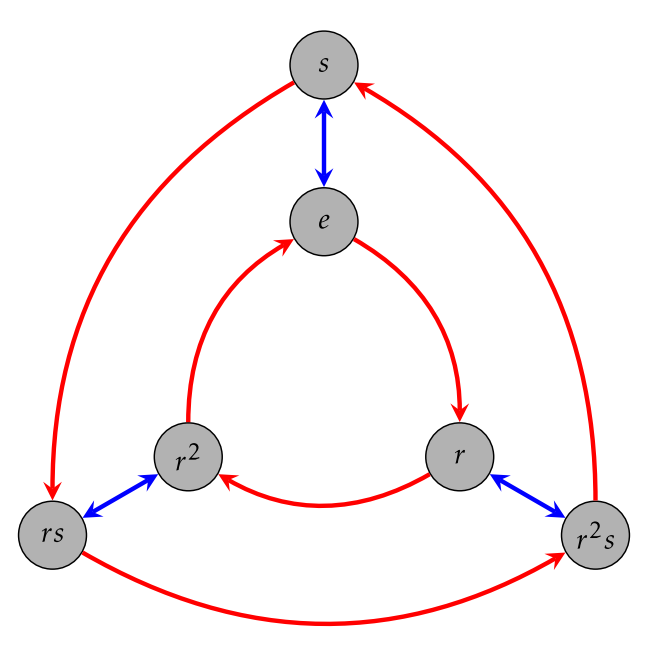
Dejar\(R_6\) denotar el grupo de simetrías rotacionales de un hexágono regular y dejar que\(r\) sea rotación en\(60^{\circ}\) sentido horario. No es muy difícil ver eso\(R_6=\langle r\rangle\) y\(|R_6|=6\). El diagrama de Cayley para\(R_6\) con grupo electrógeno\(\{r\}\) se da en la Figura\(\PageIndex{7}\).
- ¿Es\(R_6\) cíclico?
- ¿Es\(R_6\) abeliano?
- Escribe\(r^{-1}\) como una palabra en\(r\).
- ¿Puedes encontrar una palabra más corta para describir\(r^8\)?
- ¿\(r^2\)Genera el grupo?
- ¿\(r^5\)Genera el grupo?
Ahora, construyamos algunos diagramas de Cayley para promover nuestra intuición.
Construya un diagrama de Cayley para cada uno de los siguientes grupos utilizando el conjunto generador especificado.
- \(S_2\)con grupo electrógeno\(\{s\}\) (ver Problema 2.5.3)
- \(R_4\)con grupo electrógeno\(\{r\}\) (ver Problema 2.2.4)
- \(V_4\)con grupo electrógeno\(\{v,h\}\) (ver Problema 2.5.4)
- \(D_3\)con grupo electrógeno\(\{r,s\}\) (ver Problema 2.2.5)
- \(D_3\)con grupo electrógeno\(\{s,s'\}\) (ver Problema 2.4.3)
- \(S_3\)con grupo electrógeno\(\{s_1,s_2\}\) (ver Problema 2.2.7)
- \(D_4\)con grupo electrógeno\(\{r,s\}\) (ver Problema 2.2.6)
Los diagramas de Cayley no solo son visualmente atractivos, sino que proporcionan un mapa para el grupo en cuestión. Es decir, proporcionan un método para navegar por el grupo. Seguir secuencias de flechas nos dice cómo lograr una acción neta. No obstante, cada diagrama de Cayley depende mucho del conjunto de generadores que se escojan para generar el grupo. Si cambiamos el grupo electrógeno, podemos terminar con un diagrama Cayley de aspecto muy diferente. Por ejemplo, compare los diagramas Cayley para los\(D_3\) que construyó en las partes (d) y (e) de Problema\(\PageIndex{5}\).
Antes de cerrar esta sección, abordemos algunos problemas más.
Considera al grupo\((\mathbb{Z},+)\).
- Construya una porción del diagrama Cayley para\((\mathbb{Z},+)\) con grupo electrógeno\(\{1\}\).
- Construya una porción del diagrama Cayley para\((\mathbb{Z},+)\) con grupo electrógeno\(\{-1\}\). ¿Cómo se compara este diagrama con el de la parte (a)?
- Resulta que\(\mathbb{Z}=\langle 2,3\rangle\). Construya una porción del diagrama Cayley para\((\mathbb{Z},+)\) con grupo electrógeno\(\{2,3\}\).
Supongamos\(G\) que es un grupo. Supongamos que\(S\) y\(S'\) son dos conjuntos diferentes que generan\(G\). Si dibujas el diagrama de Cayley para\(G\) usar\(S\) y luego dibujas el diagrama de Cayley para\(G\) usar\(S'\), ¿qué características de las dos gráficas son las mismas y cuáles son potencialmente diferentes?
Considera los diagramas que se dan en las figuras\(\PageIndex{8}\) y\(\PageIndex{9}\). Explique por qué ninguno de estos diagramas podría ser el diagrama de Cayley para un grupo.
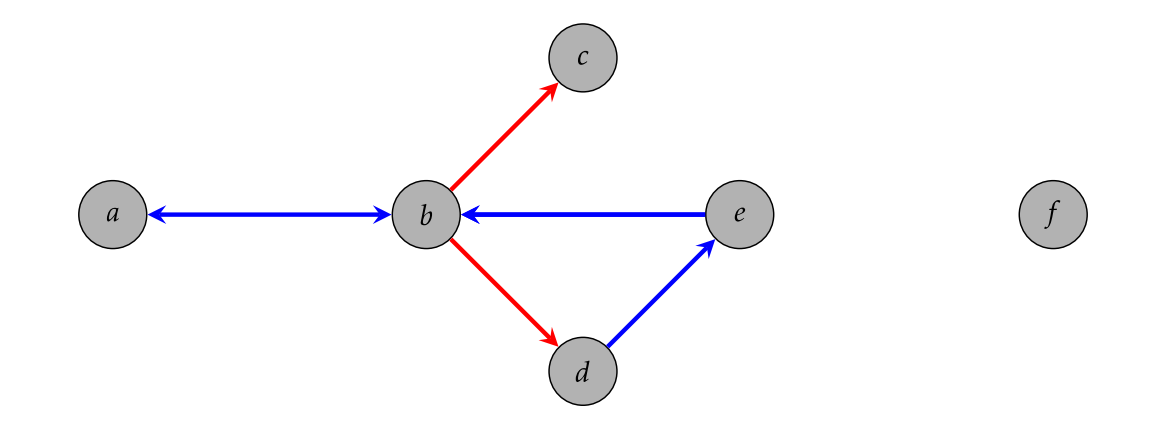
Al pensar en el problema anterior, probablemente conjeturaste los siguientes teoremas de pareja.
Si\(G\) es un grupo con grupo generador\(S\), entonces para cada\(g\in G\) y\(s\in S\), hay exactamente una flecha con color\(c_s\) apuntando de\(s^{-1}g\) a\(g\) y exactamente una flecha con color\(c_s\) apuntando de\(g\) a\(sg\).
Si\(G\) es un grupo con grupo generador\(S\), entonces se conecta el diagrama Cayley para\(G\) con grupo\(S\) generador. Es decir, por cada par de vértices\(g\) y\(h\), hay un camino de flechas hacia adelante o hacia atrás que conectan\(g\) y\(h\). *
- *
-
Pista: Primero considere el caso cuando cualquiera\(g\) o\(h\) es la identidad\(e\).
Considere el diagrama de Cayley para\(D_3\) con grupo generador\(\{r,s\}\) que se da en la Figura\(\PageIndex{10}\). Observe que etiquetamos la esquina inferior derecha del diagrama de Cayley con la palabra\(r^2s\). Esto significa que primero seguimos una flecha azul\(e\) y luego dos flechas rojas. No obstante, también podríamos llegar a este vértice haciendo primero una flecha roja de\(e\) seguida de una flecha azul. Entonces, también podríamos haber etiquetado este vértice con la palabra\(sr\). El final es ese\(r^2s=sr\). Este tipo de ecuaciones de grupo se llaman relaciones.
Descubrimos esta relación comenzando en\(e\) y luego viajando una secuencia de flechas para llegar al vértice en la esquina inferior derecha. No obstante, observe que seguir una flecha azul y luego dos rojas siempre es lo mismo que seguir una flecha roja y luego una flecha azul independientemente de en qué vértice empecemos. Es decir, la relación local que\(r^2s=sr\) comienza en se\(e\) mantiene globalmente en todo el diagrama de Cayley.
Los diagramas Cayley para grupos siempre tendrán esta simetría uniforme. Es decir, cualquier patrón local en el diagrama aparece globalmente a lo largo del diagrama.
Dejar\(G\) ser un grupo con grupo generador\(S\) y considerar el diagrama Cayley correspondiente. Supongamos que\[s_{x_1}s_{x_2}\cdots s_{x_n}=s_{y_1}s_{y_2}\cdots s_{y_m}\] es una relación en\(G\), donde cada\(s_{x_i}\) y\(s_{y_j}\) es o bien un elemento de\(S\) o la inversa de un elemento de\(S\). Explique lo que significa que esta relación se mantenga globalmente en todo el diagrama de Cayley para\(G\).
Probablemente hayas notado el siguiente teorema mientras juegas con ejemplos.
Supongamos que\(G\) es un grupo finito con conjunto generador\(S\) y considera el diagrama Cayley correspondiente. Porque\(s\in S\), si seguimos una secuencia de flechas (hacia adelante) de color\(c_s\) fuera de\(e\), eventualmente terminamos de nuevo\(e\) después de un número finito de pasos.
Supongamos que\(\{g_1,\ldots,g_n\}\) es un conjunto generador para un grupo\(G\).
- Explicar por qué también\(\{g^{-1}_1,\ldots,g^{-1}_n\}\) es un grupo electrógeno para\(G\).
- ¿Cómo se\(\{g_1,\ldots,g_n\}\) compara el diagrama Cayley para\(G\) con grupo generador con el diagrama Cayley con grupo generador\(\{g^{-1}_1,\ldots,g^{-1}_n\}\)?
Cerramos esta sección con dos problemas que le piden pensar en la estructura de los diagramas Cayley para grupos cíclicos y grupos abelianos.
Supongamos que\(G\) es un grupo cíclico con generador\(g\in G\).
- Si\(G\) es finito, ¿qué conclusiones puedes sacar sobre el diagrama Cayley para\(G\) con grupo generador\(\{g\}\)?
- Si\(G\) es infinito, ¿qué conclusiones puedes sacar sobre el diagrama de Cayley para\(G\) con grupo generador\(\{g\}\)?
Supongamos que\(G\) es un grupo abeliano con grupo generador\(S\) y considera el diagrama Cayley correspondiente.
- Si\(s,t\in S\), entonces ¿qué relación debe ser cierta sobre las flechas correspondientes?
- ¿Es cierto lo contrario de su reclamo en la parte (a)? Es decir, si cada par de flechas en el diagrama Cayley para\(G\) tiene la propiedad que indicó anteriormente, ¿el grupo será abeliano?


