2.5: Mesas de Grupo
- Page ID
- 117777
Recordemos que podríamos representar una operación binaria en un conjunto finito usando una tabla. Dado que los grupos tienen operaciones binarias en su núcleo, podemos representar un grupo finito (es decir, un grupo con muchos elementos finitamente) usando una tabla, llamada tabla de grupo. Por ejemplo, la tabla de grupos para\(D_3\) se da a continuación, donde hemos utilizado\(\{r,s\}\) como conjunto generador (ver Problema 2.4.2).
\ (\ begin {array} {c|c|c|c|c|c|c}
* & e & r & r^ {2} & s & s r & s r^ {2}\
\ hline e & e & r & r^ {2} & s & s r & s r^ {2}\
\ hline r & r & r^ {2} & s r & s r^ {2} & s & s r\\
\ hline r^ {2} & r^ {2} & e & r & s r & s r^ {2} & s\
\ hline s & s r & s r & s r^ {2} & e & r & r^ {2}
\\ hline s r & s r & s r^ {2} & s & r^ {2} & e & r
\\ hline s {2} & s r^ {2} & s & s r & amp; r & r^ {2} & e
\ end {array}\)
Como recordatorio, nuestra convención es que si\(x\) aparece en fila\(i\) y\(y\) aparece en columna\(j\), entonces fila\(i\) “times” columna\(j\) dará como resultado el elemento determinado por \(xy\), donde como de costumbre seguimos nuestra convención de derecha a izquierda. Es decir,\(xy\) significa que aplicamos\(y\) primero y después\(x\) (como en la composición de la función).
Dado un grupo arbitrario\(G\), probablemente deberíamos decir, “una tabla de grupo para\(G\)" y no “la tabla de grupos para”\(G\). La razón de esto es que si elegimos un orden diferente de los elementos (por ejemplo, las filas de intercambio 1 y 4, que también intercambian las columnas 1 y 4), entonces la tabla se vería ligeramente diferente. Además, si hubiéramos elegido un conjunto generador diferente, entonces los nombres de los elementos se verían diferentes. Independientemente, la tabla aún captura la misma información sobre la operación binaria. Debido a que cada tabla posible para un grupo dado transmite la misma información sobre la arquitectura del grupo, las personas pueden referirse a cualquier tabla para el grupo como “la” tabla. Independientemente del orden de los demás elementos del grupo, es práctica estándar enumerar primero la identidad. Es decir, pondremos siempre\(e\) en la fila superior y la columna más a la izquierda.
Para cada uno de los siguientes grupos, identifique un conjunto generador y luego cree la tabla de grupos.
- \(R_4\)
- \(D_4\)
- \(S_3\)
Dada la tabla para un grupo, ¿cómo se puede identificar qué elementos son inversos entre sí? ¿Esto te dice algo sobre qué elemento debe aparecer en cada fila y columna de la tabla de grupo?
Presentemos un par de nuevos grupos.
Considera el grupo simétrico\(S_2\) que consiste en las acciones netas que permutan las posiciones de dos monedas (sin voltearlas) que están sentadas lado a lado en una línea. \(s\)Sea la acción que intercambie las posiciones de las dos monedas.
- Verifica eso\(S_2=\langle s\rangle\). ¿Cuál es el orden de\(S_2\)?
- Crear la tabla de grupo para\(S_2\).
- ¿Es\(S_2\) abeliano?
Considera un rectángulo (que puede ser o no un cuadrado) orientado de manera que un lado sea paralelo al suelo. Deja\(h\) ser la simetría que refleja el rectángulo sobre la línea media horizontal y deja\(v\) ser la simetría que refleja el rectángulo sobre la línea media vertical. Definir\(V_4:=\langle v, h\rangle\). Este grupo se llama el grupo Klein (o Vierergruppe, que es alemán para “cuatro grupos”) después del matemático alemán Felix Klein (1849—1925).
- Verifica eso\(|V_4|=4\) describiendo las simetrías en el grupo.
- Crear la tabla de grupo para\(V_4\).
- ¿Es\(V_4\) abeliano?
- ¿Es\(V_4\) cíclico?
Quizás notaste al crear las tablas anteriores que cada elemento del grupo aparecía exactamente una vez en cada fila y columna, respectivamente. Esto es cierto en general para los grupos.
Si\((G,*)\) es un grupo finito, entonces cada elemento de\(G\) aparece exactamente una vez en cada fila y cada columna, respectivamente, en cualquier tabla de grupo para\(G\).
También podemos usar tablas para definir grupos. Por ejemplo, considere la siguiente tabla en el conjunto\(A=\{e,a,b,c\}\).
\ (\ begin {array} {c|c|c|c|c}
* & e & a & b & c\
\ hline e & e & a & b & c\
\ hline a & a & e & c & b\
\ hline b & b & b & b & b & c & a & a\
\ hline c & c & b & a & e
\ end {array}\)
¿Esta es una mesa para un grupo? Primero, vemos que la operación binaria determinada por la tabla está cerrada. Segundo, vemos que\(e\) está actuando como la identidad. Ya que cada fila y columna tiene el elemento de identidad\(e\) apareciendo, sabemos que cada elemento tiene una inversa (¿ves por qué eso sigue?). Lo único que queda por verificar es la asociatividad. Imagina por un momento lo que esto conlleva. Es desordenado ¿verdad?! Y esto es sólo para un grupo de orden 4.
Agradecidamente, podemos confiar en algunos conocimientos previos para ayudar con la asociatividad. Resulta que si se mira de cerca, la tabla de grupo para\(V_4\) se ve la “misma” que la tabla anterior. ¿Qué queremos decir con “lo mismo” aquí? Los nombres de los elementos son diferentes (excepto para\(e\)), pero
el producto de los elementos correspondientes arroja el resultado correspondiente.
Para ver a lo que me refiero, coloquemos ambas tablas con blanco, rojo, azul y verde de tal manera que cada elemento corresponda a un color único. Si elegimos nuestros colores sabiamente, es fácil ver que ambas mesas tienen la misma estructura.
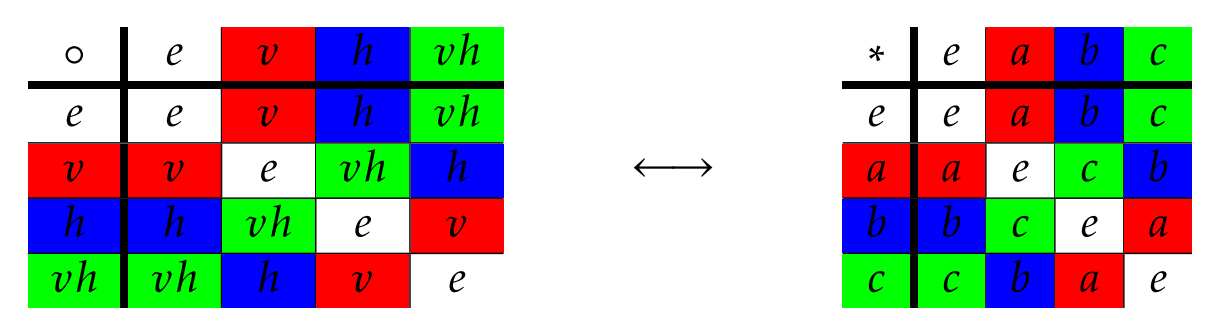
Como ya sabemos que\(V_4\) es un grupo, sabemos que la operación binaria para\(V_4\) es asociativa. Esta discusión verifica que\((A,*)\) sea un grupo.
Es importante señalar que si no hubiéramos elegido nuestros colores sabiamente, entonces quizás los colorantes de las dos mesas no estarían de acuerdo. Además, si hubiéramos hecho las mismas elecciones de color para los elementos, pero luego reorganizamos columnas y filas de una tabla, los colores de las dos tablas no estarían de acuerdo. Esto no implica nada. El punto es si podemos conseguir que las mesas coincidan.
¿Es posible colorear la tabla de grupo para\(R_4\) que coincida con la coloración de\(V_4\)? Explica tu respuesta.


