3.2: Celosías de subgrupos
- Page ID
- 117719
Uno de los objetivos de esta sección es lograr una mejor comprensión de la estructura de los grupos mediante el estudio de sus subgrupos.
Supongamos que quisiéramos encontrar todos los subgrupos de un grupo finito\(G\). Los teoremas 3.1.2 y 3.1.3 nos dicen que\(\{e\}\) y\(G\) en sí mismos son subgrupos de\(G\), pero puede haber otros. El teorema 3.1.1 nos dice que si queremos encontrar otros subgrupos de\(G\), necesitamos encontrar subconjuntos no vacíos de\(G\) que estén cerrados y contengan todas las inversas necesarias. Entonces, un método para encontrar subgrupos sería encontrar todos los posibles subconjuntos no vacíos de\(G\) y luego ir sobre determinar qué subconjuntos son subgrupos verificando si un subconjunto dado está cerrado bajo inversos y cerrado bajo la operación de\(G\). Es probable que esto consuma bastante tiempo.
Otro enfoque sería utilizar el hecho de que cada subgrupo\(H\) de\(G\) tiene un grupo generador. Es decir, si\(H\) es un subgrupo de un grupo\(G\), entonces siempre existe un subconjunto\(S\) de\(G\) tal que\(\langle S\rangle=H\). Dado un subconjunto\(S\) de\(G\),\(\langle S\rangle\) se garantiza que se cierre bajo inversas y el funcionamiento del grupo\(G\). Entonces, podríamos determinar todos los subgrupos de\(G\) generando grupos con diversos subconjuntos\(S\) de\(G\). Por supuesto, un inconveniente es que podría requerir un poco de esfuerzo determinar qué es lo que\(\langle S\rangle\) realmente es. Otro inconveniente es que dos subconjuntos diferentes\(S\) y\(T\) pueden generar el mismo subgrupo.
Hagamos esto un poco más concreto explorando un ejemplo. Considera al grupo\(R_4\). ¿De qué son los subgrupos\(R_4\)? Dado que el orden de\(R_4\) es 4, sabemos que hay subconjuntos\(2^4-1=15\) no vacíos de\(R_4\). Algunos de estos son subgrupos, pero la mayoría no lo son. Los teoremas 3.1.2 y 3.1.3 garantizan que\(\{e\}\) y\(R_4\) en sí mismos son subgrupos de\(R_4\). Eso es 2 de 15 hasta el momento. ¿Hay otros? Hagamos una búsqueda exhaustiva jugando con grupos electrógenos. Ciertamente podemos ser más eficientes, pero a continuación enumeramos todos los subgrupos posibles que podemos generar usando subconjuntos de\(R_4\). Al escanear la lista, deberías tomarte un momento para convencerte de que la lista es precisa.
\ (\ begin {array} {ll}
\ langle e\ rangle=\ {e\} &\ izquierda\ langle r, r^ {3}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}\
\ langle r\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\} &\ izquierda\ langle r^ {2}, r^ {3}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}\
\ izquierda\ langle r^ {2}\ derecha\ rangle=\ izquierda\ {e, r^ {2}\ derecha\} &\ izquierda\ langle e, r, r^ {2}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}\\ izquierda
\ langle r^ {3}\ derecha\ rangle=\ izquierda\ rangle=\ izquierda\ {e, r^ {3}, r^ {2}, r\ derecha\} &\ izquierda\ langle e, r, r^ {3}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}\
\ langle e, r\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\} &\ izquierda\ langle e, r^ {2}, r^ {3}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}\
\ izquierda\ langle e, r^ {2}\ derecha\ rangle=\ izquierda\ {e, r^ {2}\ derecha\} &\ izquierda\ langle r, r^ {2}, r^ {3}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}\
\ izquierda\ langle e , r^ {3}\ derecha\ rangle=\ izquierda\ {e, r^ {3}, r^ {2}, r\ derecha\} &\ izquierda\ langle e, r, r^ {2}, r^ {3}\ derecha\ rangle=\ izquierda\ {e, r, r^ {2}, r^ {3}\ derecha\}
\ final {matriz}\)
Hagamos algunas observaciones. Al escanear la lista, solo vemos tres subgrupos distintos:\[\{e\}, \{e,r^2\},\{e,r,r^2,r^3\}.\] De 15 subconjuntos no vacíos de\(R_4\), solo 3 subconjuntos son subgrupos. Nuestra búsqueda exhaustiva garantiza que estos son los únicos subgrupos de\(R_4\). También vale la pena señalar que si un subconjunto contiene uno\(r\) o\(r^3\), entonces ese subconjunto genera todos\(R_4\). La razón de esto es que\(\{r\}\) y cada uno\(\{r^3\}\) son grupos generadores mínimos para\(R_4\). De manera más general, observamos que si aumentamos el tamaño del subconjunto generador usando un elemento que ya estaba contenido en el subgrupo generado por el conjunto, entonces no obtenemos nada nuevo. Por ejemplo, considere\(\langle r^2\rangle=\{e,r^2\}\). Ya que\(e\in\langle r^2\rangle\), no obtenemos nada nuevo al incluirlo\(e\) en nuestro grupo generador. Esto lo podemos afirmar como un hecho general.
Seamos\(G\) un grupo y dejemos\(g_1,g_2,\ldots,g_n\in G\). Si\(x\in\langle g_1,g_2,\ldots,g_n\rangle\), entonces\(\langle g_1,g_2,\ldots,g_n\rangle = \langle g_1,g_2,\ldots,g_n,x\rangle\).
En el teorema anterior, no estamos alegando que\(\{g_1,g_2,\ldots,g_n\}\) sea un grupo generador para\(G\) —aunque este puede ser el caso. En cambio, simplemente están haciendo una declaración sobre el subgrupo\(\langle g_1,g_2,\ldots,g_n\rangle\), sea lo que sea.
Podemos capturar la relación general entre los subgrupos de un grupo\(G\) usando una red de subgrupos. Dado un grupo\(G\), la red de subgrupos de\(G\) es el conjunto parcialmente ordenado cuyos elementos son los subgrupos de\(G\) con la relación de orden parcial que se establece inclusión. Es común representar la red de subgrupos para un grupo usando un diagrama de Hasse. El diagrama Hasse de la red de subgrupos se dibuja de la siguiente manera:
- Cada subgrupo\(H\) de\(G\) es un vértice.
- Los vértices correspondientes a subgrupos con orden menor se colocan más bajos en el diagrama que los vértices correspondientes a subgrupos con mayor orden. En particular, el vértice para\(\{e\}\) se coloca en la parte inferior del diagrama y el vértice para\(G\) se coloca en la parte superior.
- Hay una ventaja que va de\(H\) a\(K\) si\(H\leq K\) y no hay subgrupo\(L\) tal que\(H\leq L\leq K\) con\(L\neq H,K\).
Observe que hay una trayectoria ascendente de aristas en el diagrama de Hasse desde\(H\) hasta\(K\) si y solo si\(H\leq K\). Por conveniencia no haremos distinción entre la celosía del subgrupo para un grupo\(G\) y el diagrama de Hasse correspondiente.
El diagrama de Hasse para la red de subgrupos para\(R_4\) se da en la Figura\(\PageIndex{1}\).
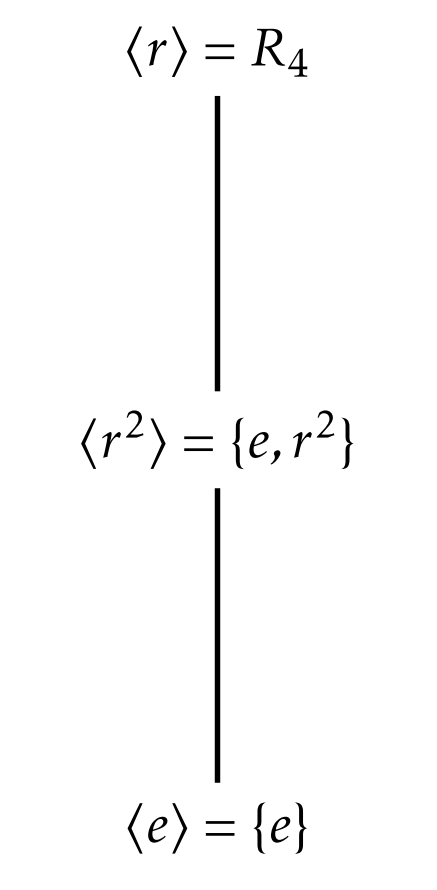
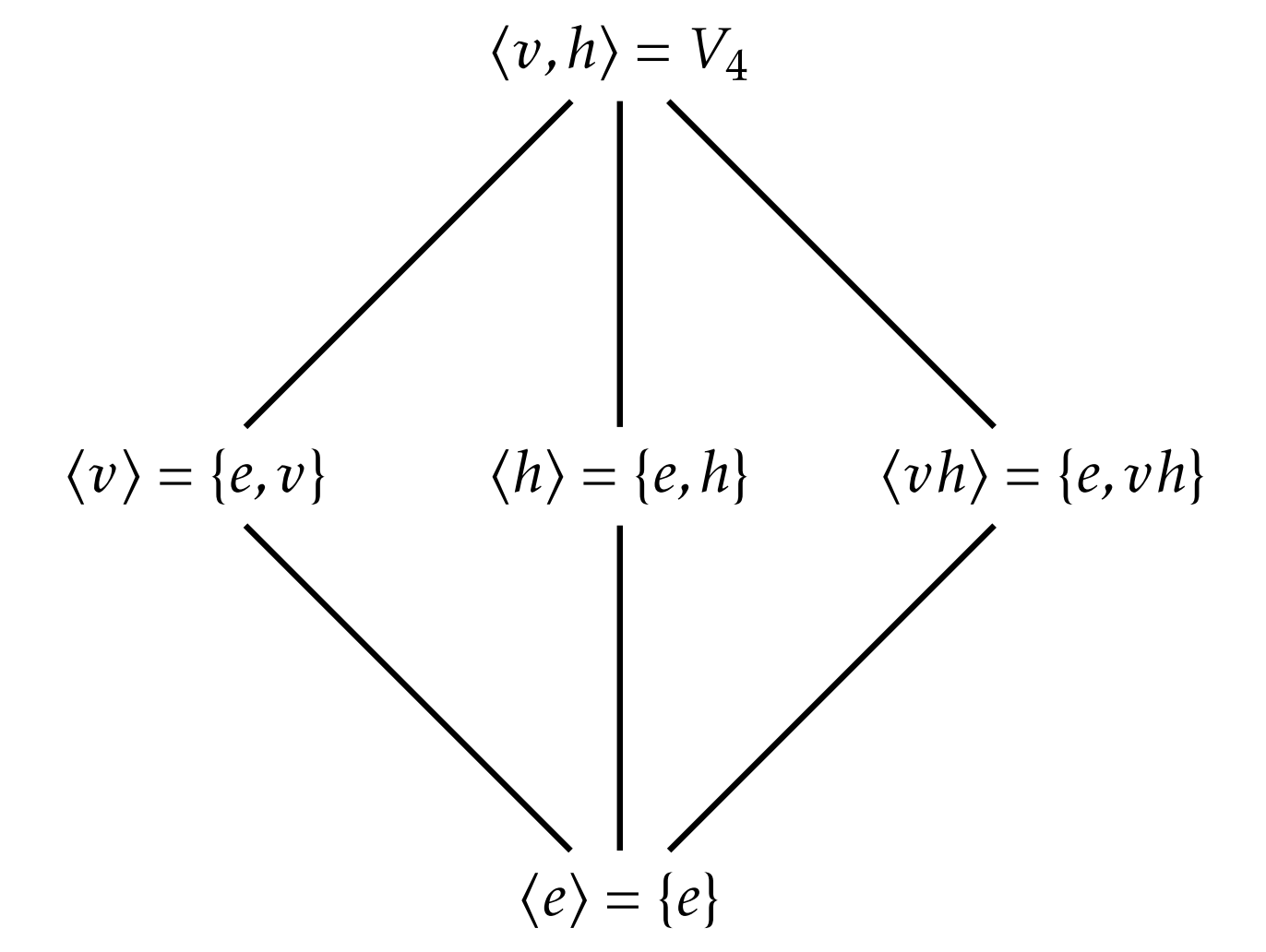
Veamos con qué podemos hacer\(V_4=\{e,v,h,vh\}\). Mediante una búsqueda exhaustiva, encontramos que existen cinco subgrupos:
\(\langle e \rangle = \{e\}\)
\(\langle h \rangle = \{e,h\}\)
\(\langle v \rangle = \{e,v\}\)
\(\langle vh \rangle = \{e,vh\}\)
\(\langle v,h \rangle = \langle v,vh\rangle = \langle h, vh\rangle= \{e,v,h,vh\}=V_4\)
Para cada subgrupo anterior, hemos utilizado conjuntos de generación mínimos para determinar el subgrupo. La red del subgrupo para\(V_4\) se da en la Figura\(\PageIndex{2}\). Observe que no hay bordes entre\(\langle v\rangle, \langle h\rangle\), y\(\langle vh\rangle\). La razón de esto es que ninguno de estos grupos son subgrupos entre sí.
Los dos teoremas siguientes proporcionan una visión más profunda de la estructura general de los subgrupos de un grupo.
Si\(G\) es un grupo tal que\(H,K\leq G\), entonces\(H\cap K\leq G\). Además,\(H\cap K\) es el subgrupo más grande contenido en ambos\(H\) y\(K\).
Resulta que no podemos simplemente sustituir “intersección” por “unión” en el teorema anterior.
Proporcionar un ejemplo de un grupo\(G\) y subgrupos\(H\) y\(K\) tal que no\(H\cup K\) sea un subgrupo de\(G\).
Si\(G\) es un grupo tal que\(H,K\leq G\), entonces\(\langle H\cup K\rangle\leq G\). Además,\(\langle H\cup K\rangle\leq G\) es el subgrupo más pequeño que contiene tanto\(H\) y\(K\).
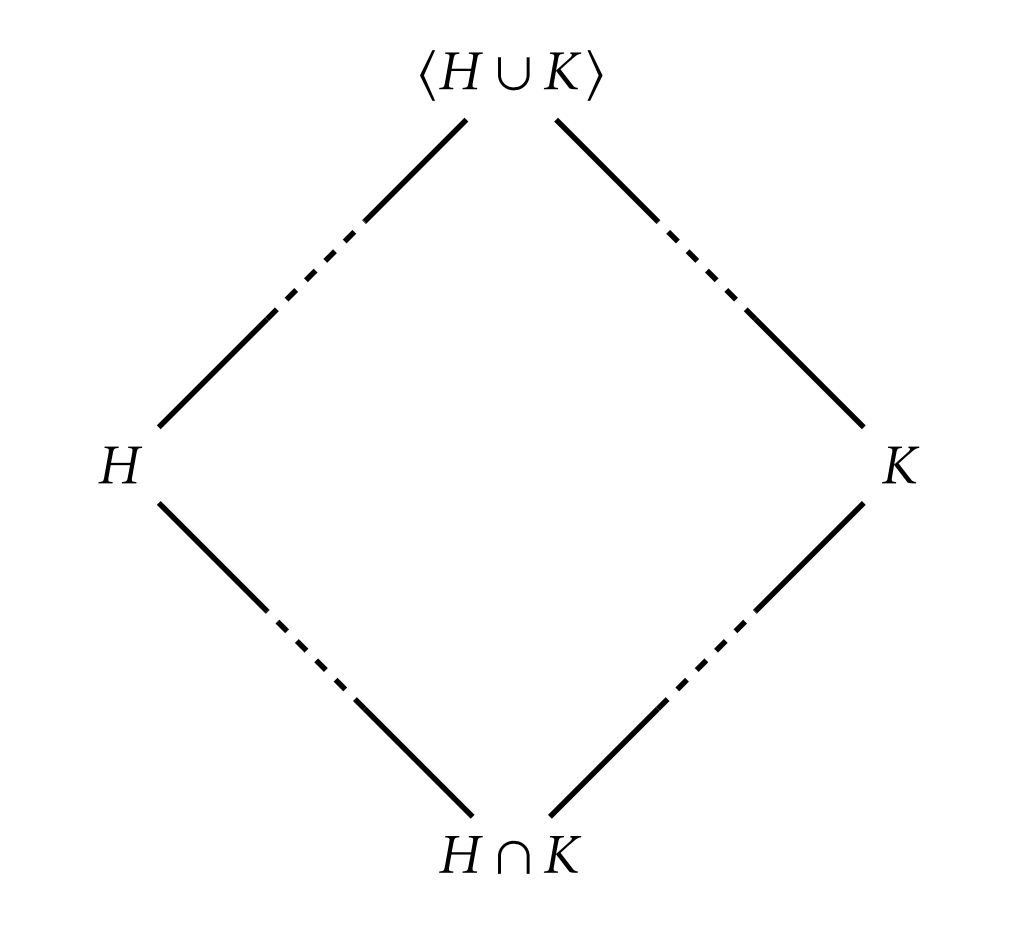
Teoremas\(\PageIndex{2}\) y\(\PageIndex{3}\) justifican el uso de la palabra “celosía” en “entramado de subgrupos”. En general, una celosía es un conjunto parcialmente ordenado en el que cada dos elementos tienen un encuentro único (también llamado un mayor límite inferior o infimum) y una unión única (también llamada límite mínimo superior o supremo). En el caso de una celosía de subgrupo para un grupo\(G\), el encuentro de subgrupos\(H\) y\(K\) es\(H\cap K\) y la unión es\(\langle H\cup K\rangle\). La figura\(\PageIndex{3}\) ilustra el encuentro (teorema\(\PageIndex{2}\)) y la unión (teorema\(\PageIndex{3}\)) en el caso cuando\(H\) y no\(K\) son comparables.
En los siguientes problemas, se le pide crear celosías de subgrupos. Al hacer esto, trata de minimizar la cantidad de trabajo que se necesita para llegar a todos los subgrupos.
Encuentra todos los subgrupos de\(R_5=\{e,r,r^2,r^3,r^4\}\) (donde\(r\) está la rotación en sentido horario de un pentágono regular por\(72^{\circ}\)) y luego dibuja la celosía del subgrupo para\(R_5\).
Encuentra todos los subgrupos de\(R_6=\{e,r,r^2,r^3,r^4,r^5\}\) (donde\(r\) está la rotación en sentido horario de un hexágono regular por\(60^{\circ}\)) y luego dibuja la celosía del subgrupo para\(R_6\).
Encuentra todos los subgrupos de\(D_3=\{e,r,r^2,s,sr,sr^2\}\) (donde\(r\) y\(s\) son las simetrías habituales de un triángulo equilátero) y luego dibuja la celosía del subgrupo para\(D_3\).
Encuentra todos los subgrupos de\(S_3=\langle s_1, s_2\rangle\) (donde\(s_1\) está la acción que intercambia las posiciones de la primera y segunda monedas y\(s_2\) es la acción que intercambia la segunda y tercera monedas; ver Problema 2.4.5) y luego dibujar la celosía del subgrupo para \(S_3\). ¿Cómo se compara tu celosía con la de Problema\(\PageIndex{4}\)? Deberías mirar hacia atrás en las partes (e) y (f) del Problema 2.6.5 y reflexionar sobre lo que acaba de suceder.
Encuentra todos los subgrupos de\(D_4=\{e,r,r^2,r^3,s,sr,sr^2,sr^3\}\) (dónde\(r\) y\(s\) son las simetrías habituales de un cuadrado) y luego dibuja la celosía del subgrupo para\(D_4\).
Encuentra todos los subgrupos de\(Q_8=\{1,-1,i,-i,j,-j,k,-k\}\) y luego dibuja la celosía del subgrupo para\(Q_8\).


