3.1: Subgrupos
- Page ID
- 117720
Recordemos la definición de “subconjunto”. ¿Qué opinas que significa “subgrupo”? Intenta llegar a una definición de potencial. Trate de no leer más antes de hacer esto.
Examine sus diagramas Cayley para\(D_4\) (con grupo generador\(\{r,s\}\)) y\(R_4\) (con grupo generador\(\{r\}\)) y haga algunas observaciones. ¿Cómo son similares y en qué se diferencian? ¿Se puede conciliar las similitudes y diferencias pensando en las acciones de cada grupo?
Ojalá, una de las cosas que notaste en el problema anterior es que podemos “ver”\(R_4\) dentro de\(D_4\). Es posible que hayas usado diferentes colores en cada caso y tal vez incluso hayas etiquetado los vértices con diferentes palabras, pero la estructura general de\(R_4\) está ahí, sin embargo.
Si ignoras las etiquetas en los vértices y solo prestas atención a la configuración de las flechas, parece que hay dos copias del diagrama Cayley para\(R_4\) en el diagrama de Cayley para\(D_4\). Aísle estas dos copias ignorando los bordes que corresponden al generador\(s\). Ahora bien, prestando mucha atención a las palabras que etiquetan los vértices del diagrama original de Cayley para\(D_4\), ¿alguno de estos grupos es por derecho propio?
Recordemos que la identidad debe ser uno de los elementos incluidos en un grupo. Si esto no se te ocurrió al hacer el problema anterior, es posible que quieras volver atrás y repensar tu respuesta. Al igual que en el problema anterior, a menudo podemos “ver” grupos más pequeños que viven dentro de grupos más grandes. Estos grupos más pequeños se denominan subgrupos.
Dejar\(G\) ser un grupo y dejar\(H\) ser un subconjunto de\(G\). Entonces\(H\) es un subgrupo de\(G\), escrito\(H\leq G\), siempre que\(H\) sea un grupo por derecho propio bajo la operación binaria heredada de\(G\).
La frase “bajo la operación binaria heredada de\(G\)" significa que para combinar dos elementos en\(H\), debemos tratar los elementos como si estuvieran en\(G\) y realizar la operación binaria de\(G\).
A la luz de Problema\(\PageIndex{3}\), escribiríamos\(R_4\leq D_4\). El segundo subdiagrama del diagrama Cayley para\(D_4\) (usando\(\{r,s\}\) como conjunto generador) que se asemeja\(R_4\) no puede ser un subgrupo porque no contiene la identidad. No obstante, como se parece mucho\(R_4\), lo llamamos clon de\(R_4\). Por conveniencia, también decimos que un subgrupo es un clon de sí mismo.
[prob:informal_subgroup_criterion] Dejar\(G\) ser un grupo y dejar\(H\subseteq G\). Si quisiéramos determinar si\(H\) es un subgrupo de\(G\), ¿podemos saltarnos la comprobación de alguno de los axiomas? ¿Qué axiomas debemos verificar?
Hagamos un poco más formales las observaciones del problema anterior.
Supongamos que\(G\) es un grupo y\(H\) es un subconjunto no vacío de\(G\). Entonces\(H\leq G\) si y sólo si (i) para todos\(h\in H\),\(h^{-1} \in H\), también, y (ii)\(H\) se cierra bajo la operación binaria de\(G\).
Observe que una de las hipótesis del Teorema\(\PageIndex{1}\) es que\(H\) sea no vacía. Esto quiere decir que si queremos probar que cierto subconjunto\(H\) es un subgrupo de un grupo\(G\), entonces una de las cosas que debemos hacer es verificar que de hecho no\(H\) esté vacío. A la luz de esto, la “Prueba de Subgrupo en Dos Pasos” probablemente debería llamarse “Prueba de Subgrupo de Tres Pasos”.
Como teoremas\(\PageIndex{2}\) e\(\PageIndex{3}\) ilustrarán, hay un par de subgrupos que cada grupo contiene.
Si\(G\) es un grupo, entonces\(\{e\}\leq G\).
El subgrupo\(\{e\}\) se conoce como el subgrupo trivial. Todos los demás subgrupos se denominan no triviales.
Seamos\(G\) un grupo. ¿Qué\(\{e\}\) aspecto tiene el diagrama Cayley para el subgrupo? ¿Qué estás usando como tu grupo generador?
Anteriormente, nos referíamos a los subgrupos como “más pequeños”. No obstante, nuestra definición no implica que este tenga que ser así.
Si\(G\) es un grupo, entonces\(G\leq G\).
Nos referimos a subgrupos que no son iguales a todo el grupo como subgrupos propios. Si\(H\) es un subgrupo apropiado, entonces podemos escribir\(H<G\).
Recordemos el teorema 2.4.1 que establece que si\(G\) es un grupo bajo\(*\) y\(S\) es un subconjunto de\(G\), entonces también\(\langle S\rangle\) es un grupo bajo\(*\). Vamos a llevar esto un paso más allá.
Si\(G\) es un grupo y\(S\subseteq G\), entonces\(\langle S\rangle \leq G\). En particular,\(\langle S\rangle\) es el subgrupo más pequeño de\(G\) contener\(S\).
El subgrupo\(\langle S\rangle\) se llama el subgrupo generado por \(S\). En el caso especial cuando\(S\) es igual a un solo elemento\(S=\{g\}\), digamos, entonces\[\langle g\rangle =\{g^k\mid k\in\mathbb{Z}\},\] que se llama el subgrupo (cíclico) generado por \(g\). Cada subgrupo se puede escribir en la forma “generado por”. Es decir, si\(H\) es un subgrupo de un grupo\(G\), entonces siempre existe un subconjunto\(S\) de\(G\) tal que\(\langle S\rangle=H\). En particular,\(\langle H\rangle=H\) para\(H\leq G\), y como caso especial, tenemos\(\langle G\rangle=G\).
Considera\(\text{Spin}_{1\times 2}\) con grupo electrógeno\(\{s_{11}, s_{22},s_{12}\}\).
- Encuentra el diagrama de Cayley para el subgrupo\(\langle s_{11}\rangle\) dentro del diagrama de Cayley para\(\text{Spin}_{1\times 2}\). Identificar todos los clones del\(\langle s_{11}\rangle\) interior\(\text{Spin}_{1\times 2}\).
- Encuentra el diagrama Cayley para el subgrupo\(\langle s_{11}, s_{22}\rangle\) dentro del diagrama Cayley de\(\text{Spin}_{1\times 2}\). Identificar los clones de\(\langle s_{11}, s_{22}\rangle\) interior\(\text{Spin}_{1\times 2}\).
Uno de los beneficios de los diagramas Cayley es que son útiles para visualizar subgrupos. No obstante, recordemos que si cambiamos nuestro conjunto de generadores, podríamos obtener un diagrama Cayley de aspecto muy diferente. El resultado de esto es que podemos ver un subgrupo en un diagrama de Cayley para un grupo dado, pero no poder verlo en el diagrama de Cayley derivado de un grupo generador diferente.
Actualmente tenemos dos diagramas Cayley diferentes para\(D_3\) (ver Problemas 2.2.5 y 2.4.3).
- ¿Puedes encontrar el diagrama Cayley para el subgrupo trivial\(\langle e\rangle\) en cualquiera de los dos diagramas Cayley para\(D_3\)? Identificar todos los clones de\(\langle e\rangle\) en ambos diagramas Cayley para\(D_3\).
- ¿Puede encontrar el diagrama de Cayley para el subgrupo\(\langle r\rangle =R_3\) en cualquiera de los dos diagramas de Cayley para\(D_3\)? Si es posible, identificar todos los clones de\(R_3\) en los diagramas de Cayley para\(D_3\).
- ¿Puedes encontrar los diagramas Cayley para\(\langle s\rangle\) y\(\langle s'\rangle\) en cualquiera de los dos diagramas de Cayley para\(D_3\)? Si es posible, identificar todos los clones de\(\langle s\rangle\) y\(\langle s'\rangle\) en los diagramas de Cayley para\(D_3\).
Considerar\(D_4\). Dejar\(h\) ser el reflejo del cuadrado sobre la línea media horizontal y dejar que\(v\) sea el reflejo sobre la línea media vertical. ¿Cuáles de los siguientes son subgrupos de\(D_4\)? En cada caso, justifica tu respuesta. Si un subconjunto es un subgrupo, intente encontrar un conjunto generador mínimo. Además, determina si puedes ver los subgrupos en nuestro diagrama de Cayley para\(D_4\) con grupo generador\(\{r,s\}\).
- \(\{e, r^2\}\)
- \(\{e,h\}\)
- \(\{e, h, v\}\)
- \(\{e, h, v, r^2\}\)
Quizás reconoció el set en la parte d del problema anterior como el grupo de cuatro Klein\(V_4\). De ello se deduce que\(V_4\leq D_4\).
Presentemos un grupo que aún no hemos visto. Definir el grupo de cuaterniones para que sea el grupo\(Q_8=\{1,-1,i,-i,j,-j,k,-k\}\) que tiene el diagrama Cayley con conjunto generador\(\{i, j, -1\}\) dado en la Figura\(\PageIndex{1}\). En este caso, 1 es la identidad del grupo.
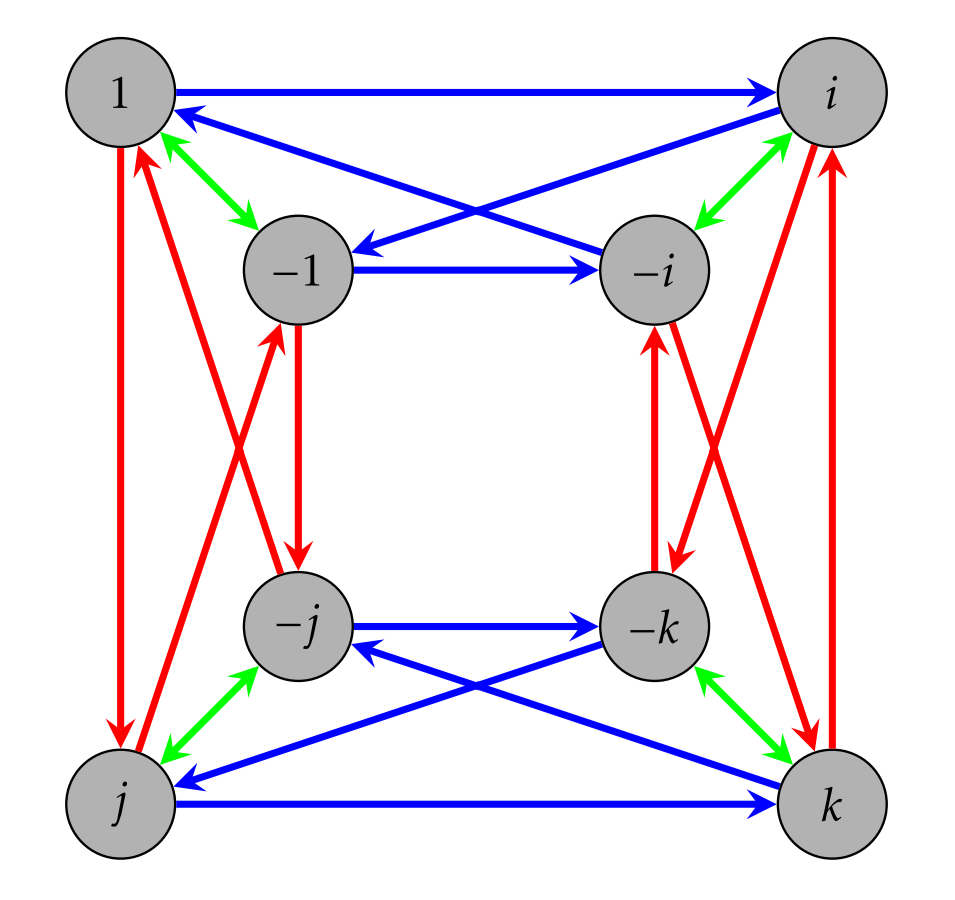
Observe que no mencioné lo que realmente hacen las acciones. Por ahora, no nos preocupemos por eso. La relación entre las flechas y los vértices nos dice todo lo que necesitamos saber. También, vamos a dar por sentado que\(Q_8\) en realidad es un grupo.
Considere el diagrama de Cayley para\(Q_8\) dado en la Figura\(\PageIndex{1}\).
- ¿Para qué flechas corresponden a qué generadores en nuestro diagrama Cayley\(Q_8\)?
- ¿A qué es\(i^2\) igual? Es decir, ¿a qué elemento de\(\{1,-1,i,-i,j,-j,k,-k\}\) es\(i^2\) igual? ¿Qué tal\(i^3\),\(i^4\), y\(i^5\)?
- ¿A qué son\(j^2\)\(j^3\)\(j^4\),, e\(j^5\) iguales?
- ¿A qué es\((-1)^2\) igual?
- ¿A qué es\(ij\) igual? ¿Qué tal\(ji\)?
- ¿Se puede determinar a qué\(k^2\) y\(ik\) son iguales?
- ¿Se puede identificar un grupo electrógeno que consta de solo dos elementos? ¿Puedes encontrar más de uno?
- ¿Qué subgrupos de\(Q_8\) puedes ver en el diagrama de Cayley en la Figura\(\PageIndex{1}\)?
- Encuentra un subgrupo del\(Q_8\) que no puedas ver en el diagrama de Cayley.
Considere\((\mathbb{R}^3,+)\), dónde\(\mathbb{R}^3\) está el conjunto de todos los vectores de fila de 3 entradas con entradas de número real (por ejemplo,\((a,b,c)\) dónde\(a,b,c\in\mathbb{R}\)) y\(+\) es la adición de vectores ordinarios. Resulta que\((\mathbb{R}^3,+)\) es un grupo abeliano con identidad\((0,0,0)\).
- Let\(H\) Ser el subconjunto de\(\mathbb{R}^3\) que consiste en vectores con la primera coordenada 0. Es\(H\) un subgrupo de\(\mathbb{R}^3\)? Demuestra tu respuesta.
- Let\(K\) Ser el subconjunto de\(\mathbb{R}^3\) que consiste en vectores cuyas entradas suman 0. Es\(K\) un subgrupo de\(\mathbb{R}^3\)? Demuestra tu respuesta.
- Construir un subconjunto de\(\mathbb{R}^3\) (diferente de\(H\) y\(K\)) que no sea un subgrupo de\(\mathbb{R}^3\).
Considerar el grupo\((\mathbb{Z},+)\) (bajo adición ordinaria).
- Demostrar que los enteros pares, escritos\(2\mathbb{Z}:=\{2k\mid k\in\mathbb{Z}\}\), forman un subgrupo de\(\mathbb{Z}\).
- Mostrar que los enteros impares no son un subgrupo de\(\mathbb{Z}\).
- Mostrar que todos los subconjuntos del formulario\(n\mathbb{Z}:=\{nk\mid k\in\mathbb{Z}\}\) para\(n\in\mathbb{Z}\) son subgrupos de\(\mathbb{Z}\).
- [prob:NZOthers] ¿Hay otros subgrupos además de los enumerados en la parte (c)? Explica tu respuesta.
- Para\(n\in \mathbb{Z}\), escribe el subgrupo\(n\mathbb{Z}\) en la notación “generado por”. Es decir, encontrar un conjunto\(S\) tal que\(\langle S\rangle =n\mathbb{Z}\). ¿Puedes encontrar más de una manera de hacerlo?
Consideremos el grupo de simetrías de un octágono regular. Este grupo se denota por\(D_8\), donde la operación es composición de acciones. El grupo\(D_8\) consta de 16 elementos (8 rotaciones y 8 reflexiones). \(H\)Sea el subconjunto que consiste en las siguientes rotaciones en sentido horario:\(0^\circ\),\(90^\circ\),\(180^\circ\), y\(270^\circ\). Determina si\(H\) es un subgrupo de\(D_8\) y justifica tu respuesta.
Considerar los grupos\((\mathbb{R},+)\) y\((\mathbb{R}\setminus\{0\},\cdot)\). Explicar por qué no\(\mathbb{R}\setminus\{0\}\) es un subgrupo de\(\mathbb{R}\) a pesar de que\(\mathbb{R}\setminus\{0\}\subseteq\mathbb{R}\) y ambos son grupos (bajo las respectivas operaciones binarias).
Si\(G\) es un grupo abeliano tal que\(H\leq G\), entonces\(H\) es un subgrupo abeliano.
¿Es cierto lo contrario del teorema anterior? Si es así, pruébalo. De lo contrario, proporcione un contraejemplo.
Como hemos visto, algunos grupos son abelianos y otros no. Si\(G\) es un grupo, entonces definimos el centro de\(G\) ser\[Z(G):=\{z\in G\mid zg=gz\text{ for all } g\in G\}.\] Notar que si\(G\) es abeliano, entonces\(Z(G)=G\). Sin embargo, si no\(G\) es abeliano, entonces\(Z(G)\) será un subconjunto adecuado de\(G\). En cierto sentido, el centro de un grupo es una medida de lo cerca que\(G\) está de ser abeliano.
Si\(G\) es un grupo, entonces\(Z(G)\) es un subgrupo abeliano de\(G\).
Encuentra el centro de cada uno de los siguientes grupos.
- \(S_2\)
- \(V_4\)
- \(S_3\)
- \(D_3\)
- \(D_4\)
- \(R_4\)
- \(R_6\)
- \(\text{Spin}_{1\times 2}\)
- \(Q_8\)
- \((\mathbb{Z},+)\)
- \((\mathbb{R}\setminus\{0\},\cdot)\)


