3.3: Isomorfismos
- Page ID
- 117727
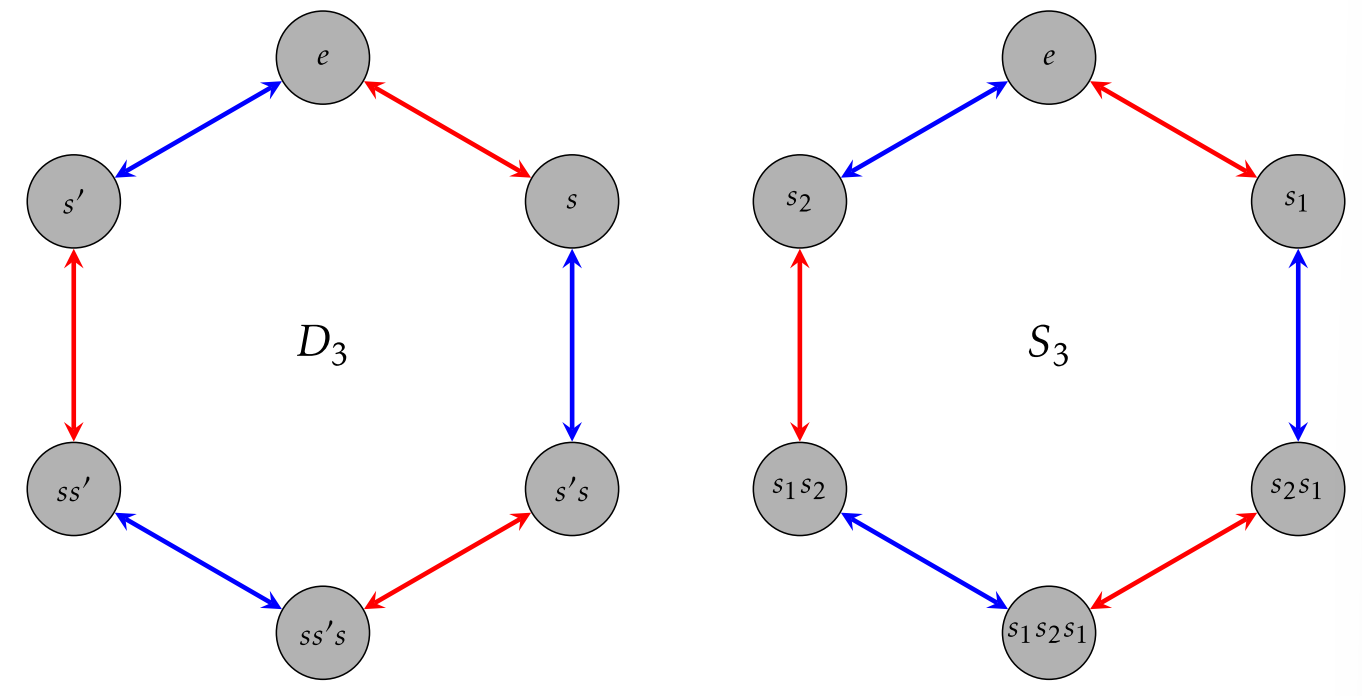
Como hemos estado explorando varios grupos, estoy seguro que te has dado cuenta de que algunos grupos parecen verse y comportarse igual. Por ejemplo, si elegimos los mismos colores para nuestras flechas e ignoramos las etiquetas en los vértices, el diagrama de Cayley para\(D_3\) con conjunto generador\(\{s,s'\}\) se ve igual que el diagrama Cayley para\(S_3\) con conjunto generador\(\{s_1, s_2\}\). Es decir, si elegimos los colores apropiados y establecemos el diagrama Cayley para\(D_3\) (con conjunto generador\(\{s,s'\}\)) encima del diagrama Cayley para\(S_3\) (con conjunto generador\(\{s_1, s_2\}\)) tal que las identidades coincidan, entonces los dos Cayley los diagramas son idénticos hasta volver a etiquetar el resto de los vértices. La figura\(\PageIndex{1}\) debe dejar esto claro. Este acto de emparejar los diagramas de Cayley establece una correspondencia entre los elementos de los dos grupos:\[\begin{aligned} e & \mapsto e\\ s & \mapsto s_1\\ s' &\mapsto s_2\\ ss' &\mapsto s_1s_2\\ s's & \mapsto s_2s_1\\ ss's & \mapsto s_1s_2s_1\end{aligned}\]
Observe que cada correspondencia es compatible con la correspondencia de los generadores, a saber:\(s \mapsto s_1\) y\(s' \mapsto s_2\). Ante esta correspondencia, no debería sorprender que las celosías subgrupales para\(D_3\) y\(S_3\) tengan la misma estructura.
El objetivo de esta sección es formalizar este fenómeno introduciendo la noción de isomorfismo. Primero, desarrollemos un poco más de intuición.
Si dos grupos\(G_1\) y\(G_2\) tenemos conjuntos generadores\(T_1\) y\(T_2\) tal que podamos colorear los bordes de los diagramas Cayley correspondientes para que los diagramas sean idénticos hasta volver a etiquetar de los vértices, entonces decimos que hay un coincidencia entre\(G_1\) y\(G_2\). Arriba, lo demostramos\(D_3\) y\(S_3\) tenemos una coincidencia. Es importante enfatizar que la existencia de un emparejamiento entre dos grupos depende de nuestra elección de grupo generador. Si dos diagramas de Cayley no se parecen, no implica inmediatamente que no haya coincidencia entre los grupos ya que podría darse el caso de que elegir diferentes grupos generadores para los dos grupos conduzca a una coincidencia.
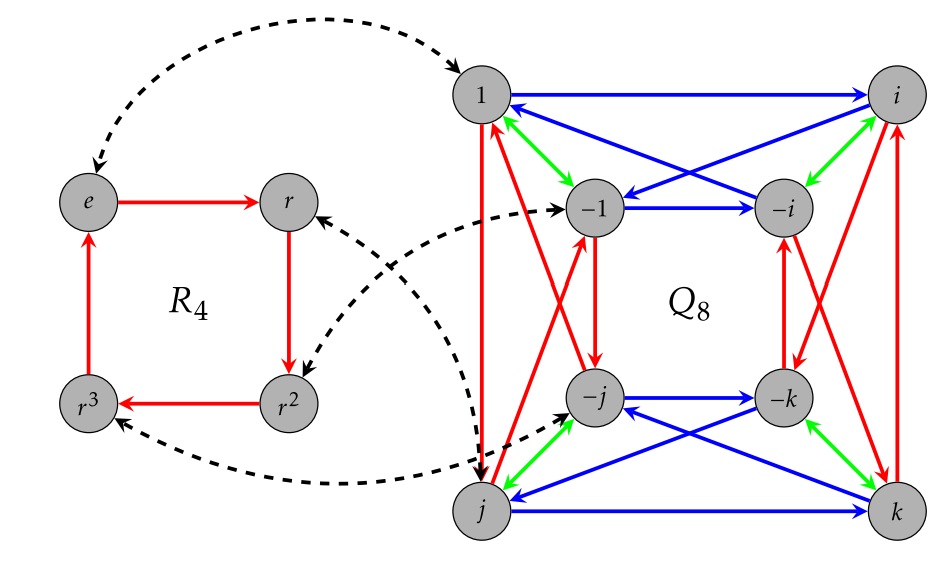
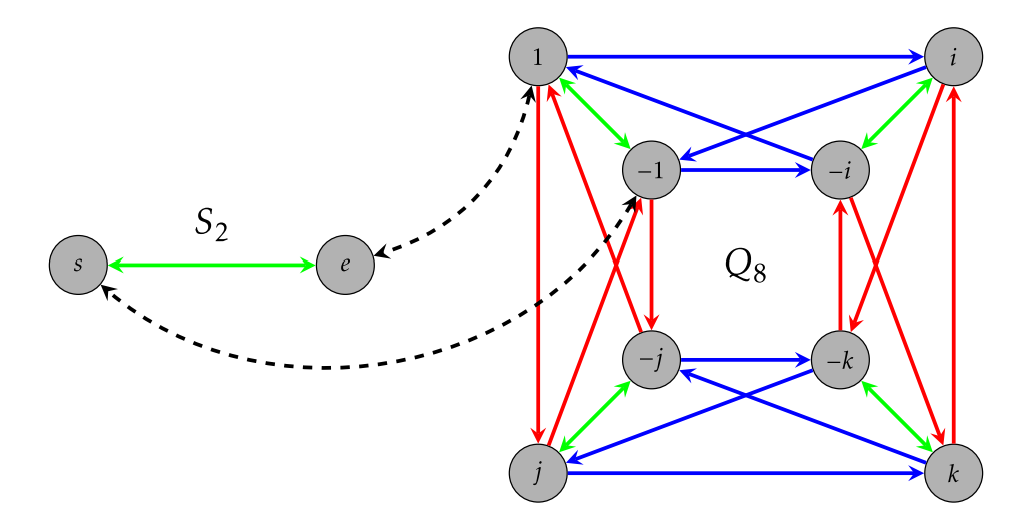
Quizás te hayas dado cuenta de que el diagrama Cayley para\(R_4\) con grupo generador\(\{r\}\) se parece al diagrama Cayley para el subgrupo\(\langle j\rangle=\{\pm 1,\pm j\}\) con grupo generador\(\{j\}\) en\(Q_8\). Es decir, hay una coincidencia entre\(R_4\) y\(\langle j\rangle\), que hemos representado en Figura\(\PageIndex{2}\). De manera similar, el diagrama de Cayley para\(S_2\) con conjunto generador\(\{s\}\) se parece al diagrama de Cayley para el subgrupo\(\langle -1\rangle=\{\pm 1\}\) con grupo generador\(\{-1\}\) en\(Q_8\). El emparejamiento entre\(S_2\) y\(\langle -1\rangle\) se representa en la Figura [Fig:ISOS2]. Es bastante fácil ver que también hay una coincidencia entre\(S_2\) y el subgrupo\(\langle v\rangle =\{e,v\}\) de\(V_4\). Dado que hay una coincidencia entre\(S_2\) y\(\langle -1\rangle\) y una coincidencia entre\(S_2\) y\(\langle v\rangle\), hay una coincidencia entre\(\langle -1\rangle\) y\(\langle v\rangle\).
Hemos visto dos diagramas Cayley diferentes para\(D_3\), uno con grupo generador\(\{s,r\}\) y otro con grupo generador\(\{s,s'\}\). Como\(\PageIndex{1}\) ilustra la Figura, existe una coincidencia entre\(D_3\) y\(S_3\) que se basa en los grupos generadores\(\{s,s'\}\) y\(\{s_1,s_2\}\), respectivamente. Encuentre una coincidencia diferente entre\(D_3\) y\(S_3\) que utilice el conjunto generador\(\{r,s\}\) para\(D_3\).
El siguiente teorema se desprende inmediatamente de la definición de coincidencia.
Si hay una coincidencia entre\(G_1\) y\(G_2\) usando los grupos generadores\(T_1\) y\(T_2\), respectivamente, entonces\(|G_1|=|G_2|\) y\(T_1\) y\(T_2\) tienen la misma cardinalidad.
Desafortunadamente, lo contrario del teorema anterior no es cierto en general. Es decir, dos grupos que tienen el mismo orden pueden o no tener una coincidencia.
Hablando vagamente, si dos grupos tienen una coincidencia, entonces los dos grupos tienen la misma estructura y características. Es decir, los dos grupos esencialmente hacen el “mismo tipo” de cosas. En particular, los elementos correspondientes en cada grupo tienen las mismas características.
Por otra parte, si un grupo tiene una propiedad que el otro no tiene, entonces los dos grupos no pueden tener una coincidencia. Por ejemplo, si un grupo es abeliano y el otro no, entonces los dos grupos no pueden tener una coincidencia. Además, para cada elemento\(g\) en un grupo con la propiedad\(g^k=e\) para algunos\(k\in \mathbb{Z}\), debe haber un elemento correspondiente en el otro grupo con la misma propiedad. De lo contrario, no puede haber un emparejamiento entre los dos grupos.
Determinar si existe una coincidencia entre\(D_4\) y\(\text{Spin}_{1\times 2}\).
Determinar si existe una coincidencia entre\(R_4\) y\(V_4\).
Determinar si existe una coincidencia entre\(D_3\) y\(R_6\).
Determinar si existe una coincidencia entre algún par de los siguientes grupos:\(R_8\) (es decir, el grupo de simetrías rotacionales de un octágono regular),\(D_4\),\(Q_8\).
Considera dos interruptores de luz en una pared uno al lado del otro. Considera el grupo de acciones que consiste en todas las acciones posibles que puedes hacer a los dos interruptores de luz. Por ejemplo, una acción es alternar el interruptor de la luz izquierda mientras se deja solo la derecha. Llamemos a este grupo\(L_2\).
- ¿Cuántas acciones distintas\(L_2\) tiene?
- ¿Se puede encontrar un grupo generador mínimo para\(L_2\)? Si es así, dale nombres a estas acciones y luego escribe todas las acciones de\(L_2\) como palabras en tu generador (es).
- Usando su grupo electrógeno de la parte (b), dibuje el diagrama Cayley correspondiente para\(L_2\).
- Determinar si hay una coincidencia entre\(L_2\) y cualquiera de\(R_4\) o\(V_4\).
Considera tres interruptores de luz en una pared uno al lado del otro. Considera el grupo de acciones que consiste en todas las acciones posibles que puedes hacer a los tres interruptores de luz. Llamemos a este grupo\(L_3\). Debería ser fácil ver que\(L_3\) tiene 8 acciones distintas.
- ¿Se puede encontrar un grupo generador mínimo para\(L_3\)? Si es así, dale nombres a estas acciones y luego escribe todas las acciones de\(L_3\) como palabras en tu generador (es).
- Usando su grupo electrógeno de la parte (a), dibuje el diagrama Cayley correspondiente para\(L_3\).
- ¿Es\(L_3\) cíclico? Justifica brevemente tu respuesta.
- ¿Es\(L_3\) abeliano? Justifica brevemente tu respuesta.
- Determinar si existe una coincidencia entre\(L_3\) y cualquiera de\(R_8\),\(D_4\),\(\text{Spin}_{1\times 2}\), o\(Q_8\).
Supongamos que\(G\) es un grupo finito y considera la tabla de grupos para\(G\). Una coloración para la tabla de grupo es una asignación de un color único a cada elemento del grupo. Por ejemplo, Figura\(\PageIndex{4}\) representa una coloración para la tabla de grupo de\(V_4\).
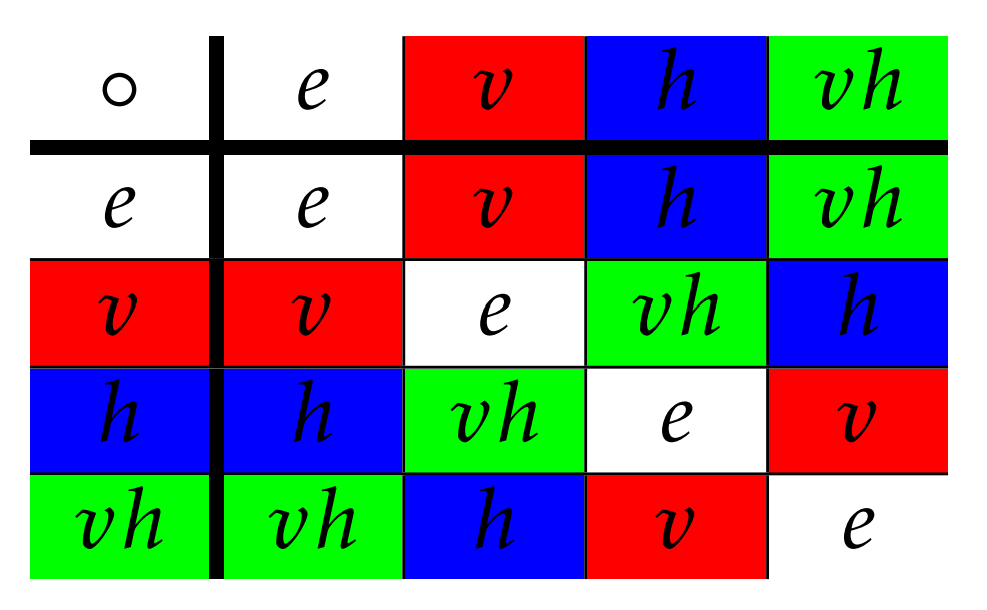
Decimos que dos grupos finitos tienen una coloración de tabla idéntica, si podemos organizar las filas y columnas de cada tabla y elegir los colores para cada tabla para que el patrón de colores sea el mismo para ambas tablas. Claramente, esto sólo es posible si los dos grupos tienen el mismo orden. En Problema 2.5.5, lo demostramos\(R_4\) y\(V_4\) nunca tenemos una coloración de mesa idéntica.
Determinar si\(V_4\) y\(L_2\) tener una coloración de mesa idéntica.
Supongamos que hay una coincidencia entre grupos finitos\(G_1\) y\(G_2\). Explique por qué\(G_1\) y\(G_2\) debe tener una coloración de mesa idéntica.
¿Es cierto lo contrario del problema anterior? Es decir, si\(G_1\) y\(G_2\) son grupos finitos que tienen una coloración de mesa idéntica, ¿habrá una coincidencia entre\(G_1\) y\(G_2\)?
Supongamos que hay una coincidencia entre\(G_1\) y\(G_2\) y supongamos que\(T_1\) es un conjunto generador para\(G_1\). Explicar por qué debe haber un conjunto generador\(T_2\) para\(G_2\) y una elección apropiada de colores de tal manera que los diagramas Cayley para\(G_1\) y\(G_2\) usando los grupos electrógenos\(T_1\) y\(T_2\), respectivamente, son idénticos hasta volver a etiquetar los vértices.
Los últimos problemas nos han llevado al siguiente teorema.
Si\(G_1\) y\(G_2\) son dos grupos finitos, entonces hay una coincidencia entre\(G_1\) y\(G_2\) si y solo si\(G_1\) y\(G_2\) tienen una coloración de tabla idéntica.
Como probablemente hayas descubierto, los emparejamientos y la coloración idéntica de la mesa (o la falta de ella) son excelentes para desarrollar la intuición sobre cuándo dos grupos tienen una estructura idéntica, pero el proceso de encontrar emparejamientos e idénticos colores de mesa es engorroso. Además, resulta no ser un enfoque muy útil para probar teoremas. Necesitamos un enfoque diferente si queremos desarrollar más la teoría general.
Si dos grupos finitos\(G_1\) y\(G_2\) tienen una coloración de tabla idéntica, entonces
el producto de los elementos correspondientes arroja el resultado correspondiente.
Esta es la esencia de lo que significa que dos grupos tengan la misma estructura.
Intentemos que esto sea un poco más preciso. Supongamos\((G_1,*)\) y\((G_2,\odot)\) son dos grupos finitos que tienen una tabla idéntica para colorear y dejar\(x_1,y_1\in G_1\). Entonces estos dos elementos tienen elementos correspondientes en la tabla de grupos para\(G_2\), digamos\(x_2\) y\(y_2\), respectivamente. En otras palabras,\(x_1\) y\(x_2\) tienen el mismo color mientras\(y_1\) y\(y_2\) tienen el mismo color. Ya que\(G_1\) se cierra bajo su operación binaria\(*\), existe\(z_1\in G_1\) tal que\(z_1=x_1*y_1\). Pero entonces debe existir un\(z_2\in G_2\) tal que\(z_2\) tenga el mismo color que\(z_1\). ¿De qué debe ser verdad\(x_2\odot y_2\)? Dado que las dos mesas exhiben el mismo patrón de color, debe ser así\(z_2=x_2\odot y_2\). Esto es lo que significa que el producto de los elementos correspondientes arroje el resultado correspondiente. La figura\(\PageIndex{5}\) ilustra este fenómeno para tablas de grupo.
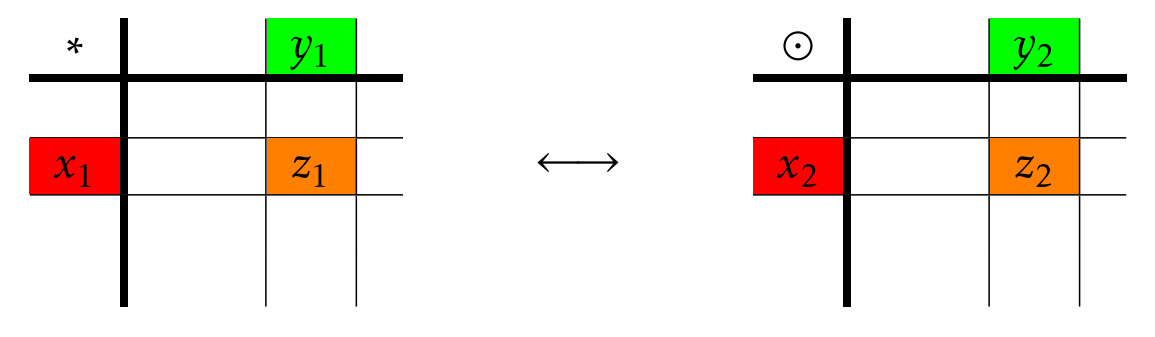
Podemos describir la tabla idéntica que coincide entre\(G_1\) y\(G_2\) usando una función. Dejar\(\phi:G_1\to G_2\) ser la función uno-a-uno y onto que mapea elementos de\(G_1\) a sus elementos correspondientes en\(G_2\). Entonces\(\phi(x_1)=x_2\),\(\phi(y_1)=y_2\), y\(\phi(z_1)=z_2\). Ya que\(z_2=x_2\odot y_2\), obtenemos\[\phi(x_1*y_1)=\phi(z_1)=z_2=x_2\odot y_2=\phi(x_1)\odot \phi(y_1).\] En resumen, debe darse el caso de que ahora\[\phi(x_1*y_1)=\phi(x_1)\odot \phi(y_1).\] estamos preparados para exponer una definición formal de lo que significa que dos grupos sean isomórficos.
Let\((G_1,*)\) y\((G_2,\odot)\) ser dos grupos. Entonces\(G_1\) es isomórfico a\(G_2\), escrito\(G_1\cong G_2\), si y solo si existe una función uno-a-uno y sobre\(\phi:G_1\to G_2\) tal que\[\label{hom_property} \phi(x*y)=\phi(x)\odot \phi(y).\] La función\(\phi\) es referida como isomorfismo . Ecuación a menudo\(\PageIndex{3}\) se conoce como la propiedad homomórfica.
Debe quedar claro a partir del desarrollo que dos grupos finitos son isomórficos si y sólo si tienen una coloración de tabla idéntica. Además, dado que dos grupos finitos tienen una coloración de tabla idéntica si y sólo si existe una coincidencia entre los dos grupos, debe darse el caso de que dos grupos sean isomórficos si y sólo si hay una coincidencia entre los dos grupos. El resultado es que tenemos tres formas diferentes de pensar lo que significa para dos grupos ser isomórficos:
- Existen conjuntos generadores para los dos grupos de tal manera que los respectivos diagramas Cayley son idénticos hasta el remarcado de los vértices.
- Existe una selección de colores y una disposición de las filas y columnas de las tablas de grupo de tal manera que las dos tablas exhiben el mismo patrón de colores.
- Existe una función biyectiva entre los dos grupos que satisface la propiedad homomórfica.
Utilizando el trabajo que hiciste anteriormente en esta sección, determina cuáles de los siguientes grupos son isomórficos entre sí:\(S_2\),\(\langle -1\rangle\) in\(Q_8\),\(R_3\),\(R_4\),\(V_4\),\(L_2\), \(\langle i\rangle\)en\(Q_8\),\(\langle sr, sr^3\rangle\) en\(D_4\)\(R_5\),\(R_6\),\(D_3\),\(S_3\)\(R_7\),\(R_8\),\(D_4\), \(\text{Spin}_{1\times 2}\),\(Q_8\),\(L_3\).
Consideremos los grupos\((\mathbb{R},+)\) y\((\mathbb{R}^+,\cdot)\), dónde\(\mathbb{R}^+\) está el conjunto de números reales positivos. Resulta que estos dos grupos son isomórficos, pero esto sería difícil de descubrir usando nuestras técnicas anteriores porque los grupos son infinitos. Definir\(\phi:\mathbb{R}\to \mathbb{R}^+\) vía\(\phi(r)=e^r\) (dónde\(e\) está la base natural, no la identidad). Demostrar que\(\phi\) es un isomorfismo.
Para cada uno de los siguientes pares de grupos, determinar si la función dada es un isomorfismo del primer grupo al segundo grupo.
- \((\mathbb{Z},+)\)y\((\mathbb{Z},+)\),\(\phi(n)=n+1\).
- \((\mathbb{Z},+)\)y\((\mathbb{Z},+)\),\(\phi(n)=-n\).
- \((\mathbb{Q},+)\)y\((\mathbb{Q},+)\),\(\phi(x)=x/2\).
Demostrar que los grupos\((\mathbb{Z},+)\) y\((2\mathbb{Z},+)\) son isomórficos.
Quizás una consecuencia sorprendente del problema anterior es que cuando se trata de grupos infinitos, un grupo puede tener un subgrupo propio al que es isomórfico. Por supuesto, esto nunca sucede con grupos finitos.
Una vez que sabemos que dos grupos son isomórficos, hay muchas cosas interesantes que podemos decir. El siguiente teorema nos dice que los isomorfismos mapean el elemento de identidad de un grupo a la identidad del segundo grupo. Esto ya estaba claro usando diagramas Cayley y tablas de grupos, pero deberías intentar probar el teorema directamente usando Definición: Isomórfico.
Supongamos que\(\phi:G_1\to G_2\) es un isomorfismo del grupo\((G_1,*)\) al grupo\((G_2,\odot)\). Si\(e_1\) y\(e_2\) son los elementos de identidad de\(G_1\) y\(G_2\), respectivamente, entonces\(\phi(e_1)=e_2\).
El siguiente teorema nos dice que los isomorfismos respetan las inversas.
Si\(\phi:G_1\to G_2\) es un isomorfismo del grupo\((G_1,*)\) al grupo\((G_2,\odot)\), entonces\(\phi(g^{-1})=[\phi(g)]^{-1}\).
Resulta que “isomórfico” (\(\cong\)) determina una relación de equivalencia sobre la clase de todos los grupos posibles. Los dos teoremas siguientes justifican que\(\cong\) sea simétrico y transitivo.
Si\(\phi:G_1\to G_2\) es un isomorfismo del grupo\((G_1,*)\) al grupo\((G_2,\odot)\), entonces la función\(\phi^{-1}:G_2\to G_1\) es un isomorfismo.
Si\(\phi:G_1\to G_2\) y\(\psi:G_2\to G_3\) son isomorfismos de los grupos\((G_1,*)\) a\((G_2,\odot)\) y\((G_2,\odot)\) a\((G_3,\star)\), respectivamente, entonces la función compuesta\(\psi\circ\phi\) es un isomorfismo de\(G_1\) y\(G_3\).
Lo único que queda por hacer para justificar el siguiente teorema es demostrar que\(\cong\) es reflexivo.
Si\(\mathcal{G}\) hay alguna colección no vacía de grupos, entonces la relación\(\cong\) es una relación de equivalencia sobre\(\mathcal{G}\).
A los matemáticos les encanta clasificar las cosas. En particular, los matemáticos quieren clasificar grupos. Se puede pensar en esta búsqueda como una taxonomía de grupos. Para simplificar la tarea, se pueden clasificar clases de isomorfismo (es decir, las clases de equivalencia determinadas por\(\cong\)) en lugar de clasificar grupos. Si dos grupos son isomórficos, entonces decimos que los grupos son iguales hasta el isomorfismo. Si hay clases de orden de\(k\) isomorfismo\(n\), entonces decimos que hay\(k\) grupos de orden\(n\) hasta el isomorfismo.
Explique por qué todos los grupos con un solo elemento son isomórficos. Justifica tu respuesta usando tablas de grupo.
A la luz del problema anterior, decimos que hay un grupo de orden uno hasta el isomorfismo.
Supongamos que\((G,*)\) es un grupo de orden 2 tal que\(G=\{e,a\}\). Complete la siguiente tabla de grupos para\(G\).
\ (\ begin {array} {l|l|l}
* & e & a\
\ hline e & &\\
\ hline a & &
\ end {array}\)
Explicar por qué cada grupo de orden 2 debe ser isomórfico para\(S_2\).
El problema anterior implica que hasta el isomorfismo, sólo hay un grupo de orden 2.
Supongamos que\((G,*)\) es un grupo de orden 3 tal que\(G=\{e,a,b\}\). Complete la siguiente tabla de grupos para\(G\).
\ (\ begin {array} {l|l|l|l}
* & e & a & b\\ hline e & & & &
\\ hline a & & & &
\\ hline a & &
\\ hline b & & & &
\ end {matriz}\)
Explicar por qué cada grupo de orden 3 debe ser isomórfico para\(R_3\).
Supongamos que\((G,*)\) es un grupo de orden 4 tal que\(G=\{e,a,b,c\}\). Suponiendo que esa\(e\) es la identidad, la primera fila y primera columna de la tabla de grupo correspondiente deben completarse de la siguiente manera.
\ (\ begin {array} {c|c|c|c|c}
* & e & a & b & c\
\ hline e & e & a & b & c\
\ hline a & a &? & &\\
\ hline b & b & & &\\
\ hline c & c & & & &
\ end {matriz}\)
La celda con el signo de interrogación no se puede llenar con un\(a\). Entonces, esta entrada debe ser o bien\(e\),\(b\), o\(c\). No obstante, debería ser fácil ver que los casos con\(b\) y\(c\) son simétricos. Así, hay dos casos: (i) se llena la entrada con el signo de interrogación\(e\), o (ii) la entrada con el signo de interrogación es sin pérdida de generalidad llena de\(b\). Completar la tabla de grupos en cada uno de estos dos casos. Son cualquiera de los grupos resultantes isomorfos a\(R_4\) o\(V_4\). ¿Qué conclusión puedes hacer sobre los grupos de orden 4?
Hasta el momento hemos visto que hay grupos únicos hasta el isomorfismo de los órdenes 1, 2 y 3, pero que hay dos grupos hasta el isomorfismo del orden 4. Una pregunta natural que hacer es: ¿cuántos grupos hay de orden\(n\)?
En un futuro capítulo podremos demostrar que sólo hay un grupo hasta el isomorfismo de orden 5, es decir, aquellos grupos isomórficos a\(R_5\).
Hemos visto tres grupos de orden 6, a saber\(R_6\),\(D_3\), y\(S_3\). Sin embargo,\(D_3\cong S_3\) si bien no\(R_6\) es isomórfico a ninguno de estos. Entonces, podemos concluir que hay al menos dos grupos hasta el isomorfismo de orden 6. Pero, ¿hay otros? Resulta que la respuesta es no, pero ¿por qué?
El grupo\(R_7\) es el grupo de simetrías rotacionales de un polígono regular de 7 lados. Este grupo tiene orden 7. ¿Hay otros grupos de orden 7 que no sean isomórficos a\(R_7\)? Resulta que la respuesta es no, pero ¿por qué?
Nos hemos encontrado con varios grupos de orden 8, a saber\(D_4\)\(\text{Spin}_{1\times 2}\),,\(Q_8\),\(R_8\), y\(L_3\). De estos, solo\(D_4\) y\(\text{Spin}_{1\times 2}\) son isomórficos. Así, hay al menos cuatro grupos hasta el isomorfismo de orden 8. ¿Son estos los únicos tipos de isomorfismo? Resulta que hay cinco grupos de orden 8 hasta el isomorfismo.
Volvamos a probar algunas declaraciones generales sobre los isomorfismos.
Supongamos que\(\phi:G_1\to G_2\) es un isomorfismo del grupo\((G_1,*)\) al grupo\((G_2,\odot)\). Si\(G_1\) es cíclico, entonces\(G_2\) es cíclico.
¿Es\(\PageIndex{7}\) cierto lo contrario del teorema? Es decir, si\(\phi:G_1\to G_2\) es un isomorfismo del grupo\((G_1,*)\) al grupo\((G_2,\odot)\) y\(G_2\) es cíclico, ¿es\(G_1\) necesariamente cíclico? Si lo contrario es cierto, entonces pruébalo. Si lo contrario es falso, proporcione un contraejemplo.
Supongamos que\(\phi:G_1\to G_2\) es un isomorfismo del grupo\((G_1,*)\) al grupo\((G_2,\odot)\). Si\(G_1\) es abeliano, entonces\(G_2\) es abeliano.
Si\(\phi:G_1\to G_2\) es una función, no necesariamente un isomorfismo, y\(X\subseteq G_1\), entonces el conjunto\[\phi(X):=\{y\in G_2\mid \text{there exists } x\in X\text{ such that }\phi(x)=y\}.\] se llama la imagen de\(X\). El siguiente teorema nos dice que la imagen de un subgrupo bajo un isomorfismo es también un subgrupo.
Si\(\phi:G_1\to G_2\) es un isomorfismo y\(H\leq G_1\), entonces\(\phi(H)\leq G_2\).
Supongamos que\(G\) es un grupo y vamos\(g\in G\). Definir\(\phi_g:G\to G\) vía\(\phi_g(x)=gxg^{-1}\). El mapa\(\phi_g\) se llama conjugación por\(g\).
Si\(G\) es un grupo y\(g\in G\), entonces la conjugación por\(g\) es un isomorfismo de\(G\) a\(G\).
Ahora que ya has probado los teoremas anteriores, es una buena idea revisar los temas clave. Si realmente estabas prestando atención, es posible que hayas notado que en algunas de las pruebas, no usamos el hecho de que la función era uno a uno y hacia a pesar de asumir que la función era un isomorfismo.
¿Para cuál de los teoremas recientes podríamos eliminar ya sea la suposición de que la función es uno a uno o la suposición de que la función está en?
Una función que satisface la propiedad homomórfica y puede o no ser uno a uno o sobre se llama homomorfismo y será objeto de un capítulo futuro.
¿Qué afirmaciones se pueden hacer sobre las redes subgrupales de dos grupos que son isomórficos? ¿Qué afirmaciones se pueden hacer sobre las redes subgrupales de dos grupos que no son isomórficos? ¿Qué afirmaciones se pueden hacer sobre dos grupos si sus celosías subgrupales no se parecen en nada?


