4.4: Grupos alternos
- Page ID
- 117738
En esta sección, describimos una clase especial de grupos de permutación. Para empezar, juguemos con algunos ejercicios.
Anote cada permutación\(S_3\) como producto de 2 ciclos de la manera más eficiente que pueda encontrar (es decir, use la menor cantidad de transposiciones posibles). Ahora, escriba cada permutación\(S_3\) como un producto de 2 ciclos adyacentes, pero no se preocupe si sus descomposiciones son eficientes. ¿Alguna observación sobre el número de transposiciones que utilizó en cada caso? Piensa en par versus impar.
Si\(\alpha_1,\alpha_2,\ldots,\alpha_k\) es una colección de 2 ciclos en\(S_n\) tal que\(\alpha_1\alpha_2\cdots\alpha_k=(1)\), entonces\(k\) debe ser parejo.
- Comprobante.
-
Supongamos que\(\alpha_1,\alpha_2,\ldots,\alpha_k\) es una colección de 2 ciclos en\(S_n\) tal que\(\alpha_1\alpha_2\cdots\alpha_k=(1)\). Tenemos que demostrar que\(k\) es parejo. Se procede por inducción fuerte. En primer lugar, es claro que la afirmación no es cierta cuando\(k=1\), sino cuando es verdad\(k=2\).
Ahora bien, supongamos que\(k>2\)\(j\leq k-1\) y si y tenemos un producto de\(j\) 2 ciclos que iguala la identidad, entonces\(j\) es par. Considerar\(\alpha_1\alpha_2\). Las únicas posibilidades son:
- \(\alpha_1\alpha_2=(a,b)(a,b)\),
- \(\alpha_1\alpha_2=(a,b)(a,c)\),
- \(\alpha_1\alpha_2=(a,b)(c,d)\),
- \(\alpha_1\alpha_2=(a,b)(b,c)\).
Si el caso (i) sucede, entonces\[(1)=\alpha_1\alpha_2\cdots\alpha_k=\alpha_3\alpha_4\cdots\alpha_k.\] Dado que la expresión de la derecha consiste en\(k-2\) factores,\(k-2\) debe ser incluso por inducción, lo que implica que\(k\) es parejo. Ahora, supongamos que estamos en uno de los casos (ii), (iii), o (iv). Observe que:
- \((a,b)(a,c)=(b,c)(a,b)\),
- \((a,b)(c,d)=(c,d)(a,b)\),
- \((a,b)(b,c)=(b,c)(a,c)\).
En cada caso, pudimos pasar\(a\) del 2 ciclo izquierdo original a un nuevo ciclo de 2 ciclos derecho. Es decir, pudimos reescribir para\(\alpha_1\alpha_2\) que\(a\) no aparezca en el 2-ciclo izquierdo. Repetir sistemáticamente este proceso para los pares\(\alpha_2\alpha_3\)\(\alpha_3\alpha_4\),,...,\(\alpha_{k-1}\alpha_k\). Si alguna vez nos encontramos con el caso (i) en el camino, entonces estamos hechos por inducción. De lo contrario, somos capaces de reescribir para\(\alpha_1\alpha_2\cdots\alpha_k\) que\(a\) sólo aparezca en el 2-ciclo más a la derecha. Pero esto implica que\(\alpha_1\alpha_2\cdots\alpha_k\) no soluciona\(a\), lo que contradice\(\alpha_1\alpha_2\cdots\alpha_k =(1)\). Esto implica que en algún momento debemos encontrar el caso (i), y por lo tanto\(k\) es incluso por inducción.
Si\(\sigma\in S_n\), entonces cada representación de transposición de\(\sigma\) tiene la misma paridad.
El teorema anterior nos dice que la siguiente definición está bien definida.
Una permutación es par (respectivamente, impar) si una de sus representaciones de transposición consiste en un número par (respectivamente, impar) de transposiciones.
Clasificar todas las permutaciones en\(S_3\) como pares o impares.
Clasificar todas las permutaciones en\(S_4\) como pares o impares.
Determinar si\((1,4,2,3,5)\) es par o impar. ¿Qué tal\((1,4,2,3,5)(7,9)\)?
Considere el\(k\) ciclo arbitrario\((a_1,a_2,\ldots, a_k)\) de\(S_n\) (con\(k\leq n\)). ¿Cuándo será este ciclo impar versus par? Justifica brevemente tu respuesta.
Conjetura una declaración sobre cuándo una permutación será par versus impar. Justifica brevemente tu respuesta.
Y por último, estamos listos para presentar a los grupos alternos.
El conjunto de todas las permutaciones pares en\(S_n\) se denota por\(A_n\) y se llama el grupo alterno.
Ya que nos referimos\(A_n\) como un grupo, ¡maldición, mejor que sea un grupo!
El conjunto\(A_n\) forma un grupo bajo composición de permutaciones y tiene orden\(n!/2\). *
- *
-
Sugerencia: Para mostrar que\(A_n\) es un grupo, argumentar que\(A_n\) es un subgrupo de\(S_n\) usar la Prueba de Subgrupo de Dos Pasos (ver Teorema [thm:subgroup_criterion]). Para demostrar eso\(|A_n|=n!/2\), demostrar que el número de permutaciones pares en\(S_n\) es el mismo que el número de permutaciones impares en\(S_n\). Aquí hay una manera de lograr esto. Definir\(f:A_n\to S_n\setminus A_n\) vía\(f(\sigma)=(1,2)\sigma\). Tenga en cuenta que\(S_n\setminus A_n\) es el conjunto de permutaciones impares en\(S_n\). Demostrar que\(f\) es una bijección.
Encuentra\(A_3\). ¿A qué grupo es\(A_3\) isomórfico?
Encuentra\(A_4\) y luego dibuja su retículo de subgrupo. ¿Es\(A_4\) abeliano?
¿Cuál es el orden de\(A_5\)? ¿Es\(A_5\) abeliano?
¿Qué órdenes de elementos ocurren en\(S_6\) y\(A_6\)? ¿Qué pasa\(S_7\) y\(A_7\)?
¿\(A_8\)Contiene un elemento de orden 15? Si es así, encuentra uno. Si no, explique por qué no existe tal elemento.
A continuación se presentan algunos datos interesantes sobre\(A_4\) y\(A_5\), que vamos a exponer sin pruebas.
- El grupo de simetrías rígidas de movimiento para un tetraedro regular es isomórfico a\(A_4\).
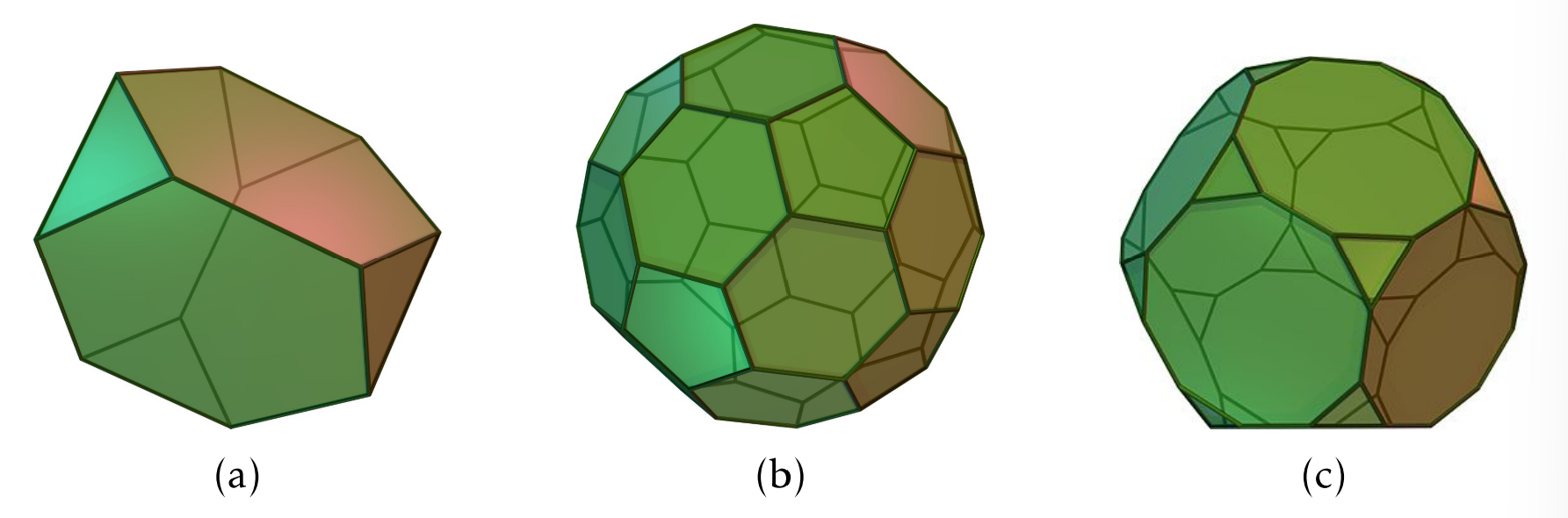
- Se puede organizar el diagrama Cayley para\(A_4\) con generadores\((1,2)(3,4)\) y\((2,3,4)\) en un tetraedro truncado, que se representa en la Figura\(\PageIndex{1}\) a.
- Se puede organizar el diagrama Cayley para\(A_5\) con generadores\((1,2)(3,4)\) y\((1,2,3,4,5)\) en un icosaedro truncado, que se da en la Figura\(\PageIndex{1}\) b. también se puede organizar el diagrama Cayley para\(A_5\) con generadores\((1,2,3)\) y \((1,5)(2,4)\)en un dodecaedro truncado visto en la Figura\(\PageIndex{1}\) c.