4.3: Grupos simétricos
- Page ID
- 117744
Recordemos los grupos\(S_2\) y\(S_3\) de Problemas 2.5.3 y 2.2.7. Estos grupos actúan sobre dos y tres monedas, respectivamente, que están en fila reordenando sus posiciones (pero no volteándolas). Estos grupos son ejemplos de grupos simétricos. En general, el grupo simétrico sobre\(n\) los objetos es el conjunto de permutaciones que reorganiza los\(n\) objetos. La operación grupal es composición de permutaciones. Seamos un poco más formales.
Una permutación de un conjunto\(A\) es una función\(\sigma:A\to A\) que es a la vez uno a uno y sobre.
Deberías tomarte un momento para convencerte de que la definición formal de una permutación concuerda con la noción de reorganizar el conjunto de objetos. La acción de no hacer nada es la permutación de identidad, es decir,\(\sigma(a)=a\) para todos\(a\in A\). Hay muchas maneras de representar una permutación. Una forma visual es usar diagramas de permutación, los cuales introduciremos a través de ejemplos.
Considere los siguientes diagramas:

Cada uno de estos diagramas representa una permutación en cinco objetos. Le he dado a las permutaciones los nombres\(\alpha\),\(\beta\),\(\sigma\), y\(\gamma\). La intención es leer los diagramas de arriba hacia abajo. Los números que etiquetan los nodos a lo largo de la parte superior identifican la posición. Seguir un borde desde la fila superior de nodos hasta la fila inferior de nodos nos dice a qué posición se mueve un objeto. Es importante recordar que los números se refieren a la posición de un objeto, no al objeto en sí. Por ejemplo,\(\beta\) es la permutación que envía el objeto en la segunda posición a la cuarta posición, el objeto en la tercera posición a la segunda posición, y el objeto en la cuarta posición a la tercera posición. Además, la permutación\(\beta\) no le hace nada a los objetos en las posiciones 1 y 5.
Describir con palabras qué son las permutaciones\(\sigma\) y\(\gamma\) qué hacen.
Dibuja el diagrama de permutación para la permutación de no hacer nada en 5 objetos. A esto se le llama la permutación de identidad. ¿Cómo se ve el diagrama de permutación de identidad en general para arbitrarios\(n\)?
El conjunto de todas las permutaciones en\(n\) los objetos se denota por\(S_n\).
Dibuja todos los diagramas de permutación para las permutaciones en\(S_3\).
¿Cuántas permutaciones distintas hay en\(S_4\)? ¿Qué tal\(S_n\) para alguno\(n\in \mathbb{N}\)?
Si\(S_n\) va a ser un grupo, necesitamos saber componer permutaciones. Esto es fácil de hacer usando los diagramas de permutación. Consideremos las permutaciones\(\alpha\) y\(\beta\) desde antes. Podemos representar la composición\(\alpha \circ \beta\) vía
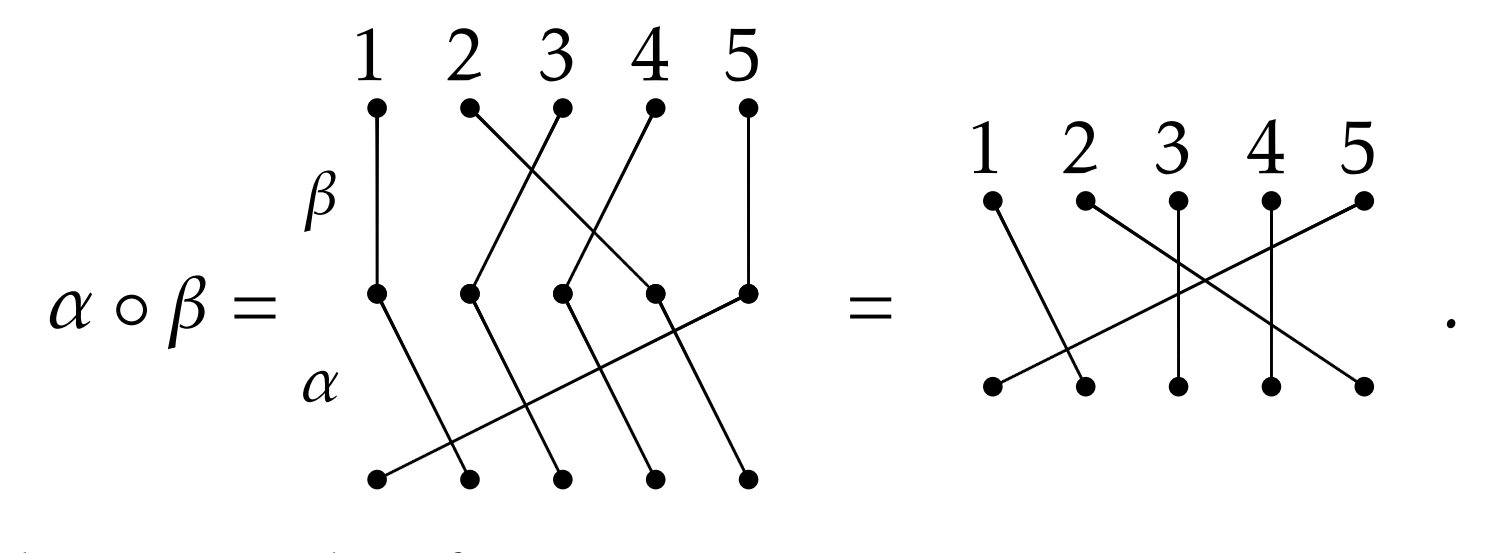
Como puedes ver al mirar la figura, para componer dos permutaciones, apilas la que va primero en la composición (por ejemplo,\(\beta\) en el ejemplo anterior) encima de la otra y simplemente sigues los bordes desde la parte superior hasta la mitad hasta la parte inferior. Si piensas en cómo funciona la composición de funciones, esto es muy natural. La permutación resultante está determinada por dónde comenzamos y dónde terminamos en la composición.
Ya sabemos que el orden de composición importa para las funciones, por lo que debería importar para la composición de las permutaciones. Para que esto quede claro como el cristal, vamos a componer\(\alpha\) y\(\beta\) en el orden opuesto. Vemos que
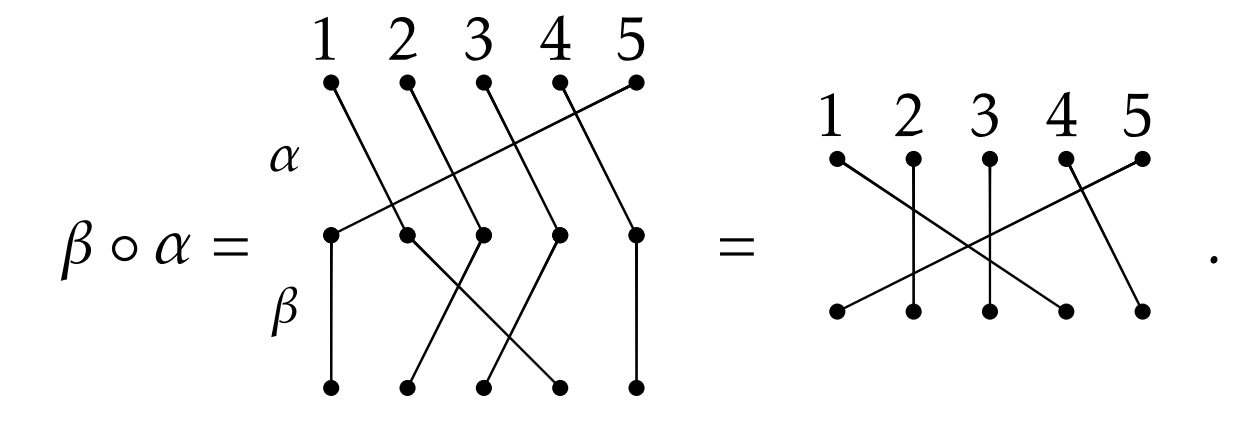
La moraleja de la historia es que la composición de las permutaciones no necesariamente conmuta.
Considerar\(\alpha\)\(\beta\),\(\sigma\),, y\(\gamma\) desde antes. ¿Puedes encontrar un par de permutaciones que sí se desplazan? ¿Puedes identificar alguna característica de tus diagramas que indique por qué se desplazaron?
Arreglar\(n\in\mathbb{N}\). Convénzate de que cualquier\(\rho\in S_n\) compuesto con la permutación de identidad (en cualquier orden) es igual\(\rho\).
Si\(S_n\) va a ser un grupo, necesitamos saber cuál es la inversa de una permutación.
Dada una permutación\(\rho\in S_n\), describir un método para construir\(\rho^{-1}\). Justificar brevemente que\(\rho \circ \rho^{-1}\) dará lugar a la permutación de identidad.
En este punto, tenemos todos los ingredientes que necesitamos para demostrar que\(S_n\) forma un grupo bajo composición de permutaciones.
El conjunto de permutaciones sobre\(n\) los objetos forma un grupo bajo la operación de la composición. Es decir,\((S_n,\circ)\) es un grupo. Además,\(|S_n|=n!\).
Tenga en cuenta que es una convención estándar omitir el símbolo de composición al escribir composiciones en\(S_n\). Por ejemplo, simplemente escribiremos\(\alpha\beta\) para denotar\(\alpha \circ \beta\).
Es divertido jugar con los diagramas de permutación, pero necesitamos una forma más eficiente de codificar la información. Una forma de hacerlo es usar la notación de ciclo. Consideremos\(\alpha, \beta, \sigma\), y\(\gamma\) en\(S_{5}\) de los ejemplos anteriores. A continuación he indicado lo que es igual cada permutación a usar notación de ciclo.
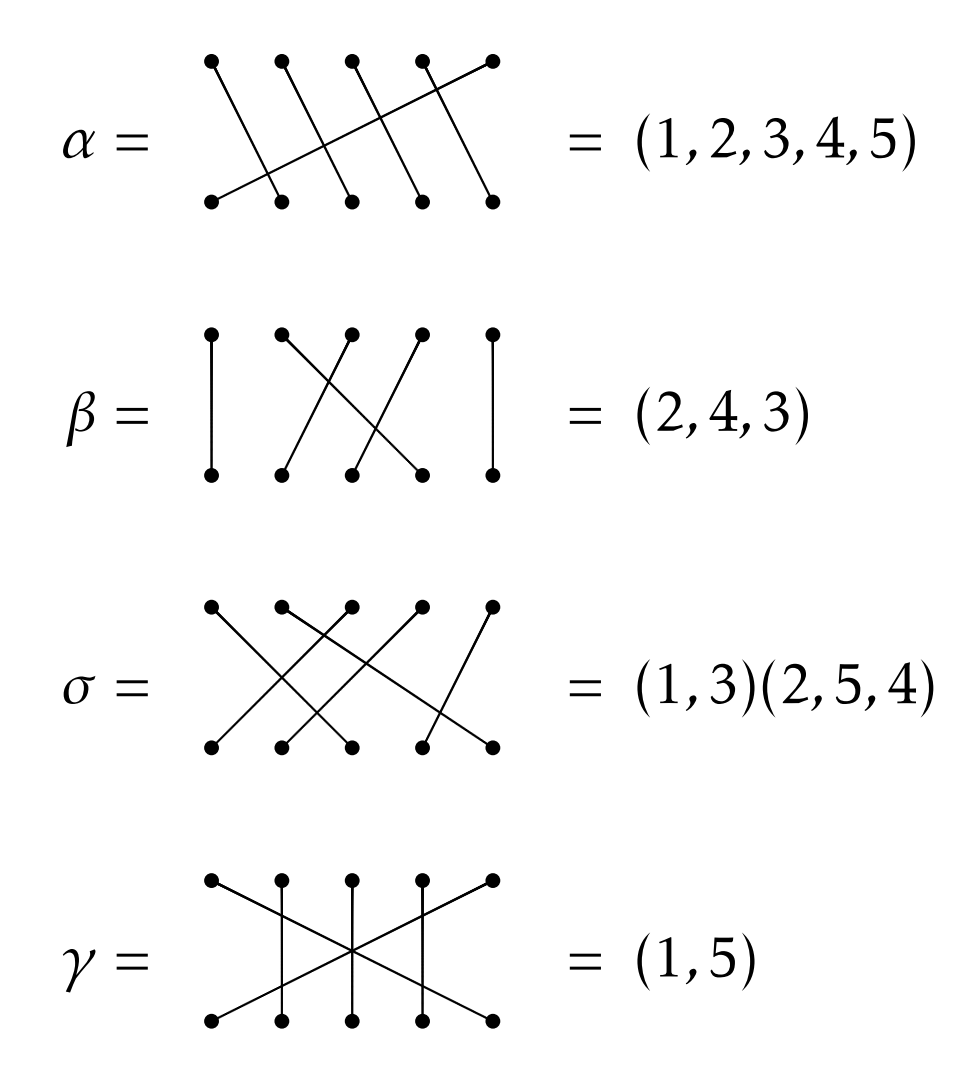
Cada cadena de números encerrada entre paréntesis se llama ciclo y si la cadena de números tiene longitud\(k\), entonces la llamamos\(k\) -ciclo. Por ejemplo,\(\alpha\) consiste en un solo ciclo de 5 ciclos, mientras que\(\sigma\) consiste en uno de 2 ciclos y uno de 3 ciclos. En el caso de\(\sigma\), decimos que\(\sigma\) es producto de dos ciclos disjuntos.
Una observación que ojalá hiciste es que si un objeto en posición\(i\) permanece sin cambios, entonces no nos molestamos en enumerar ese número en la notación de ciclo. No obstante, si quisiéramos, podríamos usar el 1-ciclo\((i)\) para denotar esto. Por ejemplo, podríamos escribir\(\beta=(1)(2,4,3)(5)\). En particular, podríamos denotar la permutación de identidad en el\(S_5\) uso\((1)(2)(3)(4)(5)\). Sin embargo, es común simplemente usar\((1)\) para denotar la identidad en\(S_n\) para todos\(n\).
Observe que el primer número que elegimos anotar para un ciclo dado es arbitrario. No obstante, los números que siguen no son negociables. Normalmente, usaríamos primero el número más pequeño posible, pero esto no es necesario. Por ejemplo, el ciclo también\((2,4,7)\) podría escribirse como\((4,7,2)\) o\((7,2,4)\).
Anote los 6 elementos en el\(S_3\) uso de la notación de ciclo.
Anote los 24 elementos en el\(S_4\) uso de la notación de ciclo.
Supongamos\(\sigma\in S_n\). Ya que\(\sigma\) es uno a uno y sobre, está claro que es posible escribir\(\sigma\) como producto de ciclos disjuntos de tal manera que cada uno\(i\in\{1,2,\ldots, n\}\) aparezca exactamente una vez.
Veamos si podemos averiguar cómo multiplicar elementos de\(S_n\) usar notación de ciclo. Considerar las permutaciones\(\alpha=(1,3,2)\) y\(\beta=(3,4)\) en\(S_4\). Para calcular la composición\(\alpha\beta=(1,3,2)(3,4)\), exploremos lo que sucede en cada posición. Ya que estamos haciendo composición de funciones, debemos trabajar nuestro camino de derecha a izquierda. Dado que 1 no aparece en la notación de ciclo para\(\beta\), lo sabemos\(\beta(1)=1\) (es decir,\(\beta\) mapas 1 a 1). Ahora, vemos qué\(\alpha(1)=3\). Así, la composición\(\alpha\beta\) mapea 1 a 3 (ya que\(\alpha\beta(1)=\alpha(\beta(1))=\alpha(1)=3\)). A continuación, debemos regresar\(\beta\) y ver qué pasa con 3—que es donde terminamos hace un momento. Vemos que\(\beta\) mapea 3 a 4 y luego\(\alpha\) mapea 4 a 4 (ya que 4 no aparece en la notación de ciclo para\(\alpha\)). Entonces,\(\alpha\beta(3)=4\). Continuando por esta vía, vemos que\(\beta\) mapas 4 a 3 y\(\alpha\) mapas 3 a 2, y así\(\alpha\beta\) mapas 4 a 2. Por último, desde\(\beta(2)=2\) y\(\alpha(2)=1\), tenemos\(\alpha\beta(2)=1\). Poniendo esto en conjunto, lo vemos\(\alpha\beta=(1,3,4,2)\). Ahora, deberías probar algunos. Las cosas se ponen un poco más difíciles si la composición de dos permutaciones da como resultado una permutación que consiste en más de un solo ciclo.
Consideremos\(\alpha\),\(\beta\),\(\sigma\), y\(\gamma\) para lo cual dibujamos los diagramas de permutación. Usando notación de ciclo, compute cada uno de los siguientes.
- \(\alpha\gamma\)
- \(\alpha^2\)
- \(\alpha^3\)
- \(\alpha^4\)
- \(\alpha^5\)
- \(\sigma\alpha\)
- \(\alpha^{-1}\sigma^{-1}\)
- \(\beta^2\)
- \(\beta^3\)
- \(\beta\gamma\alpha\)
- \(\sigma^3\)
- \(\sigma^6\)
Anote la tabla de grupos para\(S_3\) usar la notación de ciclo.
En Problema\(\PageIndex{9}\), una de las permutaciones que deberías haber anotado es\((1,2)(3,4)\). Este es un producto de dos 2 ciclos disjuntos. Cabe señalar que cada ciclo es una permutación por derecho propio. Es decir,\((1,2)\) y\((3,4)\) son cada una permutaciones. Da la casualidad de que su composición no “simplifica” más. Además, estos dos disjuntos de 2 ciclos conmutan desde\((1,2)(3,4)=(3,4)(1,2)\). De hecho, este fenómeno siempre es cierto.
Supongamos\(\alpha\) y\(\beta\) son dos ciclos disjuntos. Entonces\(\alpha\beta=\beta\alpha\). Es decir, productos de ciclos disjuntos conmutan.
Calcular las órdenes de todos los elementos en\(S_3\). Ver Problema\(\PageIndex{8}\).
Calcular las órdenes de cualquiera de doce de los elementos en\(S_4\). Ver Problema\(\PageIndex{9}\).
Calcular el orden de una permutación es bastante fácil usando la notación de ciclo una vez que descubrimos cómo hacerlo para un solo ciclo. De hecho, probablemente ya hayas adivinado el siguiente teorema.
Si\(\alpha\in S_n\) tal que\(\alpha\) consiste en un solo\(k\) -ciclo, entonces\(|\alpha|=k\).
Supongamos\(\alpha\in S_n\) tal que\(\alpha\) consiste en\(m\) ciclos disjuntos de longitudes\(k_1,\ldots, k_m\). Entonces\(|\alpha|=\text{lcm}(k_1,\ldots, k_m)\). *
- *
-
Recordemos que\(\text{lcm}(k_1,\ldots, k_m)\) es el múltiplo menos común de\(\{k_1,\ldots, k_m\}\).
¿Es cierto el teorema anterior si no requerimos que los ciclos sean disjuntos? Justifica tu respuesta.
¿Cuál es el orden de\((1,4,7)(2,5)(3,6,8,9)\)?
Dibuja la celosía del subgrupo para\(S_3\).
Ahora, usando\((1,2)\) y\((1,2,3)\) como generadores, dibuje el diagrama Cayley para\(S_3\). ¿Te pareces familiar?
Considerar\(S_3\).
- Usando\((1,2)\)\((1,3)\), y\((2,3)\) como generadores, dibuje el diagrama de Cayley para\(S_3\).
- En la parte anterior, se utilizó un conjunto generador con tres elementos. ¿Hay un grupo electróreo más pequeño? Si es así, ¿qué es?
Recordemos que hay\(4!=24\) permutaciones en\(S_4\).
- Elige cualquier 12 permutaciones de\(S_4\) y verifica que puedes escribirlas como palabras en los 2 ciclos\((1,2), (1,3), (1,4), (2,3), (2,4),(3,4)\). En la mayoría de las circunstancias, sus palabras no consistirán en productos de 2 ciclos disjuntos. Por ejemplo, la permutación se\((1,2,3)\) puede descomponer en\((1,2)(2,3)\), que es una palabra que consiste en dos 2 ciclos que resultan no ser disjuntos.
- Usando tus mismas 12 permutaciones, verifica que puedas escribirlas como palabras solo en los 2 ciclos\((1,2),(2,3),(3,4)\).
Por cierto, podría tomar algún ensayo y error para llegar a una manera de hacer esto. Además, hay más de una manera de hacerlo.
Como se insinuaron los ejercicios anteriores, los 2 ciclos juegan un papel especial en los grupos simétricos. De hecho, tienen un nombre especial. Una transposición es un solo ciclo de longitud 2. En el caso especial de que la transposición sea de la forma\((i,i+1)\), la llamamos transposición adyacente. Por ejemplo,\((3,7)\) es una transposición (no adyacente) mientras que\((6,7)\) es una transposición adyacente.
Resulta que el conjunto de transposiciones en\(S_n\) es un grupo generador para\(S_n\). De hecho, las transposiciones adyacentes forman un conjunto generador aún más pequeño para\(S_n\). Para conseguir algo de intuición, juguemos con algunos ejemplos.
Trate de escribir cada una de las siguientes permutaciones como producto de las transposiciones. No necesariamente es necesario utilizar transposiciones adyacentes.
- \((3,1,5)\)
- \((2,4,6,8)\)
- \((3,1,5)(2,4,6,8)\)
- \((1,6)(2,5,3)\)
Los productos que encontraste en el ejercicio anterior se denominan representaciones de transposición de la permutación dada.
Considere el\(k\) ciclo arbitrario\((a_1,a_2,\ldots, a_k)\) de\(S_n\) (con\(k\leq n\)). Encuentra la manera de escribir esta permutación como producto de 2 ciclos.
Considere el arbitrario de 2 ciclos\((a,b)\) de\(S_n\). Encuentra la manera de escribir esta permutación como producto de 2 ciclos adyacentes.
Los dos problemas anteriores implican el siguiente teorema.
Considerar\(S_n\).
- Cada permutación en\(S_n\) puede escribirse como un producto de transposiciones.
- Cada permutación en\(S_n\) puede escribirse como un producto de transposiciones adyacentes.
El conjunto de transposiciones (respectivamente, el conjunto de transposiciones adyacentes) de\(S_n\) forma un conjunto generador para\(S_n\).
Es importante señalar que la representación transposición de una permutación no es única. Es decir, hay muchas palabras en las transposiciones que igualarán la misma permutación. No obstante, como veremos en la siguiente sección, dadas dos representaciones de transposición para una misma permutación, el número de transposiciones tendrá la misma paridad (es decir, par versus impar).
Aquí hay dos datos interesantes que te dejaré reflexionar sobre tu propio tiempo.
- El grupo de simetrías rígidas de movimiento para un cubo es isomórfico a\(S_4\). Para convencerte de este hecho, primero prueba que este grupo tiene 24 acciones y luego reflexiona sobre la acción de\(S_4\) sobre las cuatro diagonales largas de un cubo.
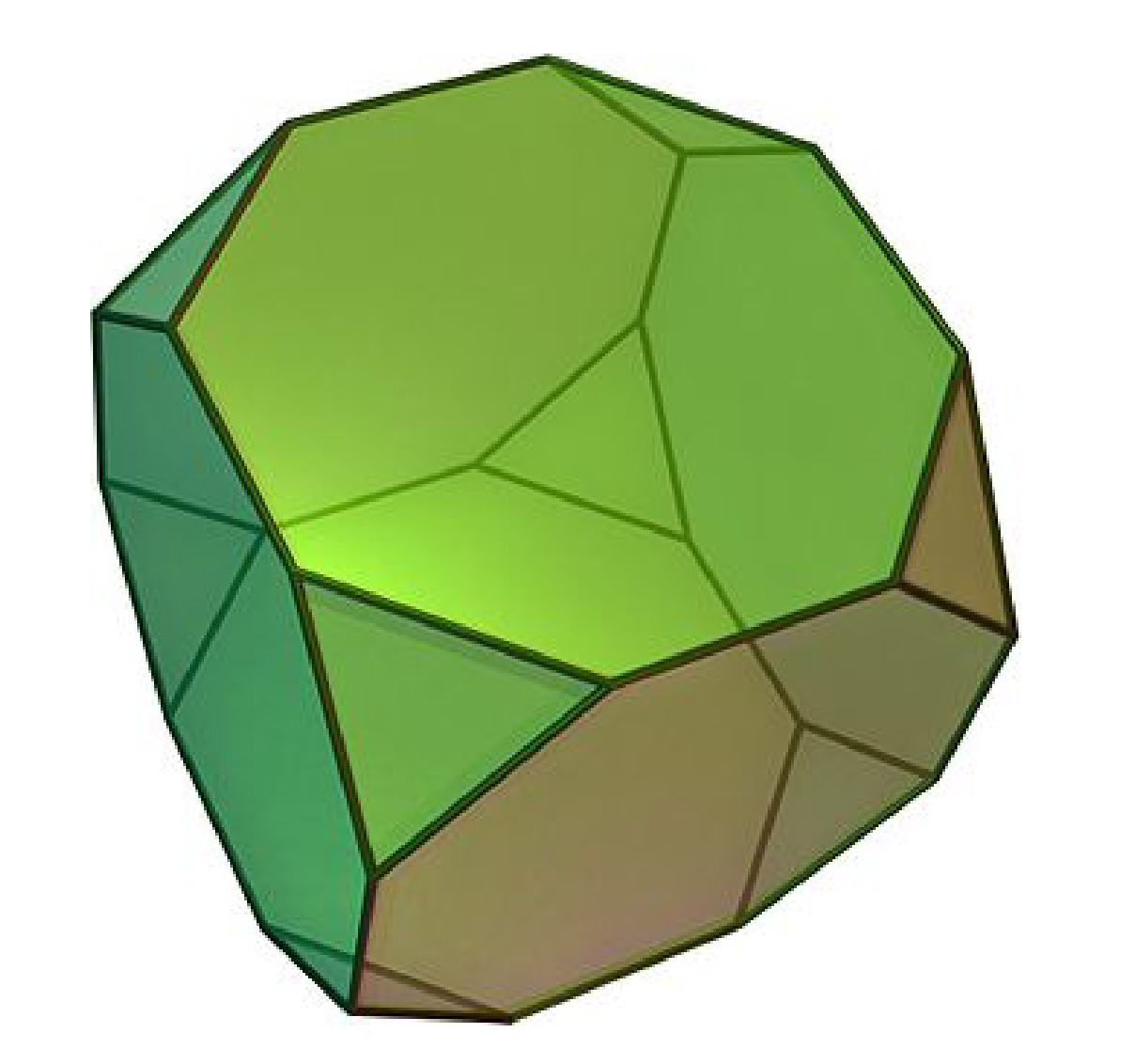
- Resulta que se puede generar\(S_4\) con\((1,2)\) y\((1,2,3,4)\). Además, se puede organizar el diagrama Cayley para\(S_4\) con estos generadores en un cubo truncado, que se representa en la Figura\(\PageIndex{5}\). Pruébalo.
Resulta que los subgrupos de grupos simétricos juegan un papel importante en la teoría de grupos.
Cada subgrupo de un grupo simétrico se denomina grupo de permutación.
La prueba del siguiente teorema no es tan mala, pero la daremos por sentada. Después de retocar algunos ejemplos, deberías tener suficiente intuición para ver por qué el teorema es cierto y cómo podría ir una posible prueba.
Cada grupo finito es isomórfico a algún grupo de permutación. En particular, si\(G\) es un grupo de orden\(n\), entonces\(G\) es isomórfico a un subgrupo de\(S_n\).
El Teorema de Cayley garantiza que cada grupo finito es isomórfico a un grupo de permutación y resulta que existe un algoritmo bastante simple para construir el grupo de permutación correspondiente. Te explicaré brevemente un ejemplo y luego te dejaré probar un par.
Considera el grupo de cuatro Klein\(V_4=\{e,v,h,vh\}\). Recordemos que\(V_4\) tiene la siguiente tabla de grupos.
\ (\ begin {array} {c|c|c|c|c}
* & e & v & h & v h\
\ hline e & e & v & v h & v h
\\ hline v & v & v h & h & h & h & v h & h & v h & v y e & v
\\ hline v h & v
; h & v & e
\ end {matriz}\)
Si numeramos los elementos\(e,v,h,\) y\(vh\) as\(1,2,3,\) y\(4\), respectivamente, entonces obtenemos la siguiente tabla.
\ (\ begin {array} {c|c|c|c|c}
& 1 & 2 & 3 & 4\
\ hline 1 & 1 & 2 & 3 & 4\\ hline 2 & 2 & 1 & 4 & 3
\\ hline 3 y 3 & 3 & 3 & 4 & 1 & 2
\\ hline 4 & 4 & 4 & 4
\\ hline 4 & 4 & 3 & 2 & amp; 1
\ end {array}\)
Comparando cada una de las cuatro columnas con la columna más a la izquierda, podemos obtener las permutaciones correspondientes. En particular, obtenemos\[\begin{aligned} e&\leftrightarrow (1)\\ v&\leftrightarrow (1,2)(3,4)\\ h&\leftrightarrow (1,3)(2,4)\\ vh&\leftrightarrow(1,4)(2,3). \end{aligned}\] ¿Ves de dónde provienen estas permutaciones? El reclamo es que el conjunto de permutaciones\(\{(1),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}\) es isomórfico a\(V_4\). En este caso particular, es bastante claro que esto es cierto. Sin embargo, se necesita algo de trabajo para demostrar que este proceso siempre resultará en un grupo de permutación isomórfica. De hecho, verificar el algoritmo es esencialmente la prueba del Teorema de Cayley.
Dado que potencialmente hay muchas formas de reorganizar las filas y columnas de una tabla dada, debería quedar claro que potencialmente hay muchos isomorfismos que podrían resultar del algoritmo descrito anteriormente.
Aquí hay otra manera de obtener un grupo de permutación que es isomórfico a un grupo dado. Consideremos de\(V_4\) nuevo. Recordemos que\(V_4\) es un subconjunto de\(D_4\), que es el grupo de simetría para un cuadrado. Alternativamente,\(V_4\) es el grupo de simetría para un rectángulo no cuadrado. Etiquete las esquinas del rectángulo 1, 2, 3 y 4 comenzando en la esquina superior izquierda y continuando en el sentido de las agujas del reloj. Recordemos que\(v\) es la acción que refleja el rectángulo sobre la línea media vertical. El resultado de esta acción es que las esquinas etiquetadas por 1 y 2 cambian de lugar y las esquinas etiquetadas por 3 y 4 cambian de lugar. Así,\(v\) corresponde a la permutación\((1,2)(3,4)\). De igual manera,\(h\) intercambia las esquinas etiquetadas por 1 y 4 y las esquinas etiquetadas por 2 y 3, y así\(h\) corresponde a la permutación\((1,4)(2,3)\). Observe que esta no es la misma respuesta que obtuvimos antes y eso está bien ya que puede haber muchas representaciones de permutación para un grupo dado. Por último,\(vh\) gira el rectángulo\(180^{\circ}\) que envía termina intercambiando esquinas etiquetadas con 1 y 3 e intercambiando esquinas etiquetadas con 2 y 4. Por lo tanto,\(vh\) corresponde a la permutación\((1,3)(2,4)\).
Considerar\(D_4\).
- Utilizando el método descrito anteriormente, encontrar un subgrupo de\(S_8\) que es isomórfico a\(D_4\).
- Etiquete las esquinas de un cuadrado 1—4. Encontrar un subgrupo de\(S_4\) que sea isomórfico\(D_4\) al considerar la acción natural de\(D_4\) en las etiquetas en las esquinas del cuadrado.
Considerar\(\mathbb{Z}_6\).
- Utilizando el método descrito anteriormente, encontrar un subgrupo de\(S_6\) que es isomórfico a\(\mathbb{Z}_6\).
- Etiquete las esquinas de un hexágono regular 1—6. Encontrar un subgrupo de\(S_6\) que sea isomórfico\(\mathbb{Z}_6\) al considerar la acción natural de\(\mathbb{Z}_6\) en las etiquetas en las esquinas del hexágono.


