1.1: Sistemas de Ecuaciones Lineales
- Page ID
- 113120
- Entender la definición\(\mathbb{R}^n\text{,}\) y lo que significa usar para\(\mathbb{R}^n\) etiquetar puntos en un objeto geométrico.
- Imágenes: soluciones de sistemas de ecuaciones lineales, conjuntos de soluciones parametrizadas.
- Palabras de vocabulario: consistente, inconsistente, conjunto de soluciones.
Durante la primera mitad de este libro de texto, nos ocuparemos principalmente de comprender las soluciones de los sistemas de ecuaciones lineales.
Una ecuación en las incógnitas\(x,y,z,\ldots\) se llama lineal si ambos lados de la ecuación son una suma de múltiplos (constantes) de\(x,y,z,\ldots\text{,}\) más una constante opcional.
Por ejemplo,
\[ \begin{split} 3x + 4y &= 2z \\ -x - z &= 100 \end{split} \nonumber \]
son ecuaciones lineales, pero
\[ \begin{split} 3x + yz &= 3 \\ \sin(x) - \cos(y) &= 2 \end{split} \nonumber \]
no lo son.
Normalmente moveremos las incógnitas al lado izquierdo de la ecuación, y moveremos las constantes hacia la derecha.
Un sistema de ecuaciones lineales es una colección de varias ecuaciones lineales, como
\[\label{eq:1}\left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6\\ 2x &-& 3y &+& 2z &=& 14\\ 3x &+& y &-& z &=& -2. \end{array}\right.\]
- Una solución de un sistema de ecuaciones es una lista de números\(x, y, z, \ldots\) que hacen que todas las ecuaciones sean verdaderas simultáneamente.
- El conjunto de soluciones de un sistema de ecuaciones es la colección de todas las soluciones.
- Resolver el sistema significa encontrar todas las soluciones con fórmulas que involucran cierto número de parámetros.
Un sistema de ecuaciones lineales no necesita tener una solución. Por ejemplo, no existen números\(x\) y\(y\) haciendo que las siguientes dos ecuaciones sean verdaderas simultáneamente:
\[\left\{\begin{array}{rrrrc} x &+& 2y &=& 3 \\ x &+& 2y &=& -3.\end{array}\right.\nonumber\]
En este caso, el conjunto de soluciones está vacío. Como esta es una propiedad bastante importante de un sistema de ecuaciones, tiene su propio nombre.
Un sistema de ecuaciones se llama inconsistente si no tiene soluciones. Se llama consistente de otra manera.
Una solución de un sistema de ecuaciones en\(n\) variables es una lista de\(n\) números. Por ejemplo,\((x,y,z) = (1,-2,3)\) es una solución de\(\eqref{eq:1}\). Como vamos a estar estudiando soluciones de sistemas de ecuaciones a lo largo de este texto, ahora es un buen momento para fijar nuestras nociones respecto a listas de números.
Línea, Plano, Espacio, Etc.
Usamos\(\mathbb{R}\) para denotar el conjunto de todos los números reales, es decir, la línea numérica. Esto contiene números como\(0, \frac 32, -\pi, 104, \ldots\)
Dejar\(n\) ser un número entero positivo. Definimos
\[ \mathbb{R}^n = \text{all ordered \(n\)-tuples of real numbers }(x_1,x_2,x_3,\ldots,x_n). \nonumber \]
Una\(n\) -tupla de números reales se llama punto de\(\mathbb{R}^n\).
En otras palabras,\(\mathbb{R}^n\) es solo el conjunto de todas las listas (ordenadas) de números\(n\) reales. Haremos dibujos de\(\mathbb{R}^n\) en un momento, pero ten en cuenta que esta es la definición. Por ejemplo,\((0, \frac 32, -\pi)\) y\((1,-2,3)\) son puntos de\(\mathbb{R}^3\).
Cuando\(n=1\text{,}\) acabamos de\(\mathbb{R}\) regresar:\(\mathbb{R}^1=\mathbb{R}\). Geométricamente, esta es la recta numérica.
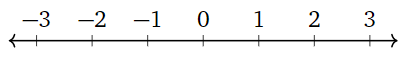
Figura\(\PageIndex{1}\)
Cuando\(n=2\text{,}\) podemos pensar en\(\mathbb{R}^2\) como el\(xy\) -avión. Podemos hacerlo porque cada punto del plano puede ser representado por un par ordenado de números reales, es decir, sus coordenadas\(x\) - y\(y\) -coordenadas.
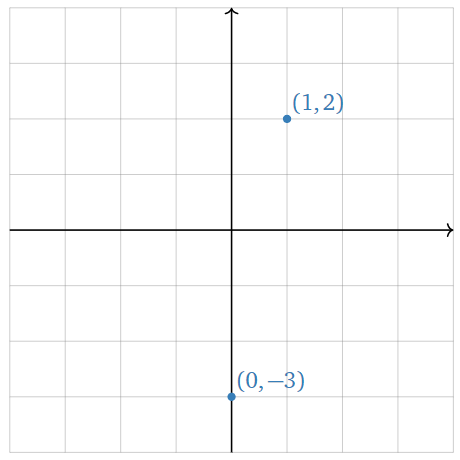
Figura\(\PageIndex{2}\)
Cuando\(n=3\text{,}\) podemos pensar en\(\mathbb{R}^3\) el espacio en el que (parece) vivir. Podemos hacerlo porque cada punto en el espacio puede estar representado por un triple ordenado de numebrs reales, es decir, sus coordenadas\(x\) -,\(y\) -, y\(z\) -coordenadas.
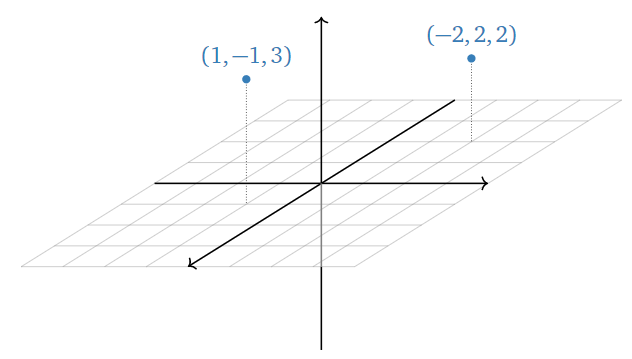
Figura\(\PageIndex{3}\)
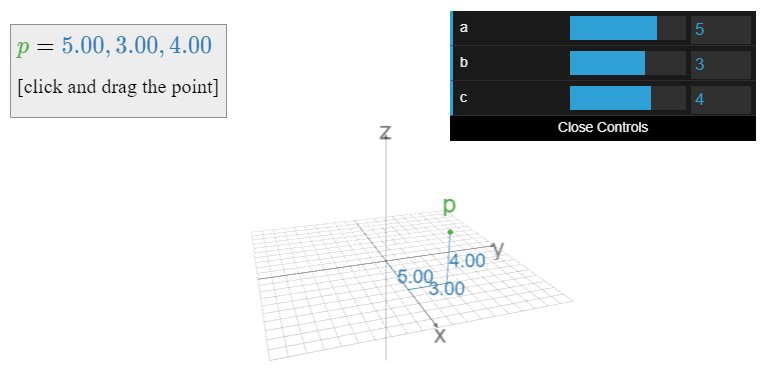
Figura\(\PageIndex{4}\): Un punto en el espacio 3, y sus coordenadas. Haga clic y arrastre el punto, o mueva los controles deslizantes.
Entonces, ¿qué es\(\mathbb{R}^4\text{?}\)\(\mathbb{R}^5\text{?}\) o o\(\mathbb{R}^n\text{?}\) Estos son más difíciles de visualizar, así que hay que volver a la definición:\(\mathbb{R}^n\) es el conjunto de todas las\(n\) tuplas ordenadas de números reales\((x_1,x_2,x_3,\ldots,x_n)\).
Siguen siendo espacios “geométricos”, en el sentido que nuestra intuición para\(\mathbb{R}^2\) y\(\mathbb{R}^3\) muchas veces se extiende a\(\mathbb{R}^n\).
Haremos definiciones y teoremas estatales que se apliquen a cualquiera\(\mathbb{R}^n\text{,}\) pero solo haremos dibujos para\(\mathbb{R}^2\) y\(\mathbb{R}^3\).
El poder de utilizar estos espacios es la capacidad de etiquetar diversos objetos de interés, como los objetos geométricos y las soluciones de sistemas de ecuaciones, por los puntos de\(\mathbb{R}^n\).
Todos los colores que puedes ver pueden ser descritos por tres cantidades: la cantidad de luz roja, verde y azul en ese color. (Los humanos son tricromáticos.) Por lo tanto, podemos usar los puntos de\(\mathbb{R}^3\) para etiquetar todos los colores: por ejemplo, el punto\((.2, .4, .9)\) etiqueta el color con intensidad\(20\%\) roja,\(40\%\) verde y\(90\%\) azul.
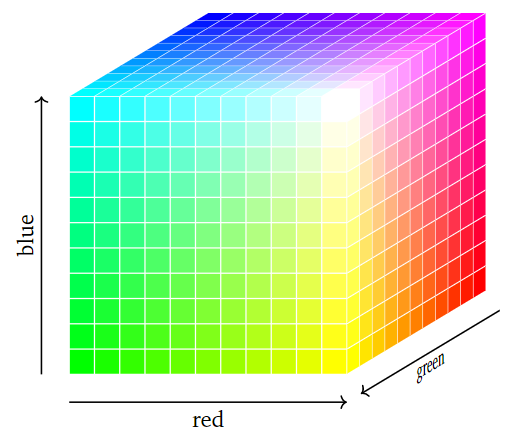
Figura\(\PageIndex{5}\)
En el Overview, podríamos haber usado\(\mathbb{R}^4\) para etiquetar la cantidad de tráfico\((x,y,z,w)\) que pasa por cuatro calles. Es decir, si hay\(10,5,3,11\) autos por hora que pasan por carreteras\(x,y,z,w\text{,}\) respectivamente, entonces esto se puede registrar por el punto\((10,5,3,11)\) en\(\mathbb{R}^4\). Esto es útil desde un punto de vista psicológico: en lugar de tener cuatro números, ahora estamos tratando con un solo dato.
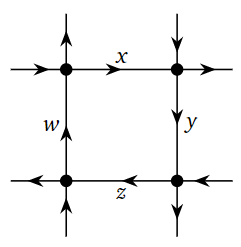
Figura\(\PageIndex{6}\)
Un código QR es un método para almacenar datos en una cuadrícula de cuadrados en blanco y negro de una manera que las computadoras puedan leer fácilmente. Un código QR típico es una\(29 \times 29\) cuadrícula. Al leer cada línea de izquierda a derecha y leer las líneas de arriba a abajo (como lees un libro) podemos pensar en un código QR como una secuencia de\(29 \times 29 = 841\) dígitos, siendo cada dígito 1 (para el blanco) o 0 (para el negro). De tal manera, todo el código QR puede considerarse como un punto en\(\mathbb{R}^{841}\). Al igual que en el Ejemplo anterior\(\PageIndex{6}\), es muy útil desde una perspectiva psicológica ver un código QR como una sola pieza de datos de esta manera.


En los ejemplos anteriores, fue útil desde una perspectiva psicológica sustituir una lista de cuatro números (que representan el flujo de tráfico) o de 841 números (que representan un código QR) por una sola pieza de datos: un punto en algunos\(\mathbb{R}^n\). Este es un concepto poderoso; a partir de la Sección 2.2, registraremos casi exclusivamente soluciones de sistemas de ecuaciones lineales de esta manera.
Imágenes de Solution Sets
Antes de discutir a continuación cómo resolver un sistema de ecuaciones lineales, es útil ver algunas imágenes de cómo se ven geométricamente estos conjuntos de soluciones.
Considera la ecuación lineal\(x+y=1\). Podemos reescribir esto como\(y = 1-x\text{,}\) lo que define una línea en el plano: la pendiente es\(-1\text{,}\) y la\(x\) -intercepción es\(1\).
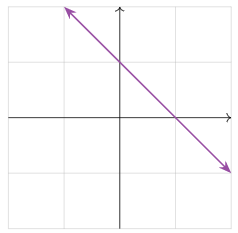
Figura\(\PageIndex{8}\)
Para nuestros propósitos, una línea es un rayo que es recto e infinito en ambas direcciones.
Considera la ecuación lineal\(x+y+z=1\). Esta es la ecuación implícita para un plano en el espacio.
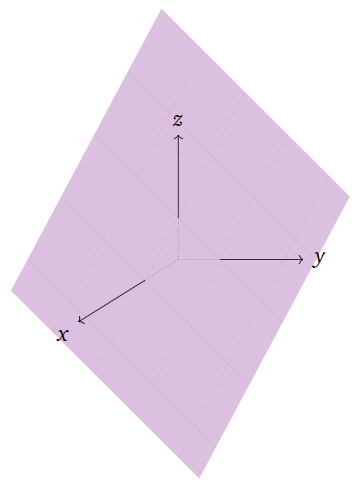
Figura\(\PageIndex{9}\)
Un plano es una hoja plana que es infinita en todas las direcciones.
La ecuación\(x+y+z+w=1\) define un “\(3\)-plano” en\(4\) el espacio, y más generalmente, una sola ecuación lineal en\(n\) variables define un “\((n-1)\)-plano” en\(n\) el espacio. Precisaremos estas declaraciones en la Sección 2.7.
Consideremos ahora el sistema de dos ecuaciones lineales
\[\left\{\begin{array}{rrrrr}\color{Violet}{x}&\color{Violet}{-}&\color{Violet}{3y}&\color{Violet}{=}&\color{Violet}{-3.} \\ \color{Green}{2x}&\color{Green}{+}&\color{Green}{y}&\color{Green}{=}&\color{Green}{8.}\end{array}\right.\nonumber\]
Cada ecuación define individualmente una línea en el plano, que se muestra a continuación.
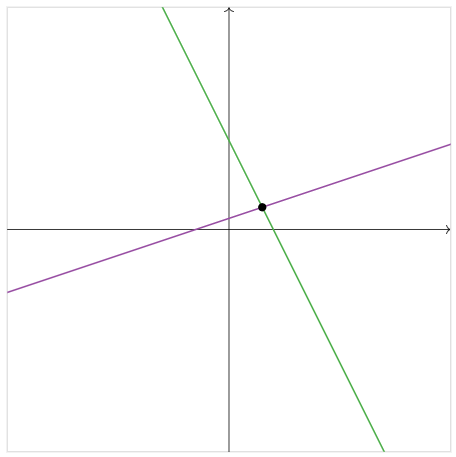
Figura\(\PageIndex{10}\)
Una solución al sistema de ambas ecuaciones es un par de números\((x,y)\) que hace que ambas ecuaciones sean verdaderas a la vez. En otras palabras, es como un punto que yace en ambas líneas simultáneamente. Podemos ver en la imagen de arriba que solo hay un punto donde se cruzan las líneas: por lo tanto, este sistema tiene exactamente una solución. (Esta solución es\((3,2)\text{,}\) como el lector puede verificar.)
Por lo general, dos líneas en el plano se cruzarán en un punto, pero claro que no siempre es así. Consideremos ahora el sistema de ecuaciones
\[\left\{\begin{array}{rrrrr}\color{Violet}{x}&\color{Violet}{-}&\color{Violet}{3y}&\color{Violet}{=}&\color{Violet}{-3.} \\ \color{Green}{x}&\color{Green}{-}&\color{Green}{3y}&\color{Green}{=}&\color{Green}{3.}\end{array}\right.\nonumber\]
Estos definen líneas paralelas en el plano.
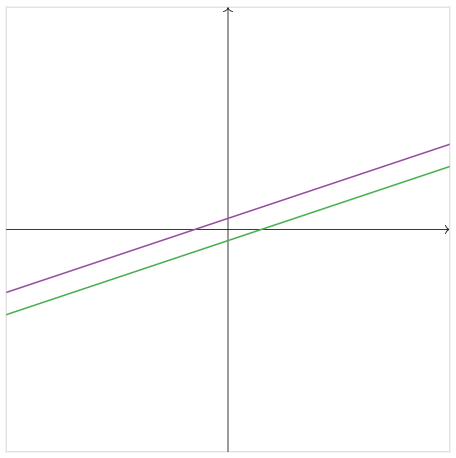
Figura\(\PageIndex{11}\)
El hecho de que las líneas no se crucen significa que el sistema de ecuaciones no tiene solución. Por supuesto, esto es fácil de ver algebraicamente: si\(x-3y=-3\text{,}\) entonces no es así tampoco puede ser así\(x-3y=3\).
Hay una posibilidad más. Considerar el sistema de ecuaciones
\[\left\{\begin{array}{rrrrr}\color{Violet}{x}&\color{Violet}{-}&\color{Violet}{3y}&\color{Violet}{=}&\color{Violet}{-3.} \\ \color{Green}{2x}&\color{Green}{-}&\color{Green}{6y}&\color{Green}{=}&\color{Green}{-6.}\end{array}\right.\nonumber\]
La segunda ecuación es un múltiplo de la primera, por lo que estas ecuaciones definen la misma línea en el plano.
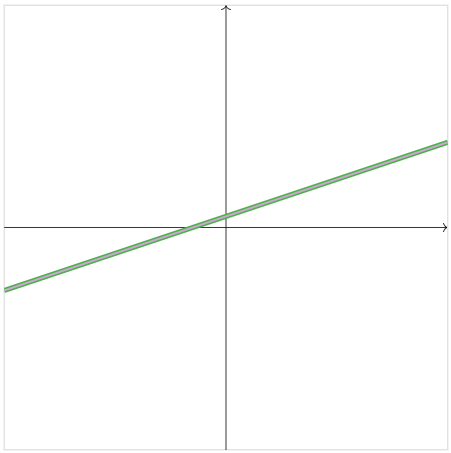
Figura\(\PageIndex{12}\)
En este caso, hay infinitamente muchas soluciones del sistema de ecuaciones.
Considerar el sistema de dos ecuaciones lineales
\[\left\{\begin{array}{rrrrr}\color{Violet}{x}&\color{Violet}{+}&\color{Violet}{y}&\color{Violet}{+}&\color{Violet}{z}&\color{Violet}{=}&\color{Violet}{1} \\ \color{Green}{x}&\color{Green}{}&\color{Green}{}&\color{Green}{-}&\color{Green}{z}&\color{Green}{=}&\color{Green}{0.}\end{array}\right.\nonumber\]
Cada ecuación define individualmente un plano en el espacio. Las soluciones del sistema de ambas ecuaciones son los puntos que se encuentran en ambos planos. Podemos ver en la imagen de abajo que los planos se cruzan en una línea. En particular, este sistema tiene infinitamente muchas soluciones.
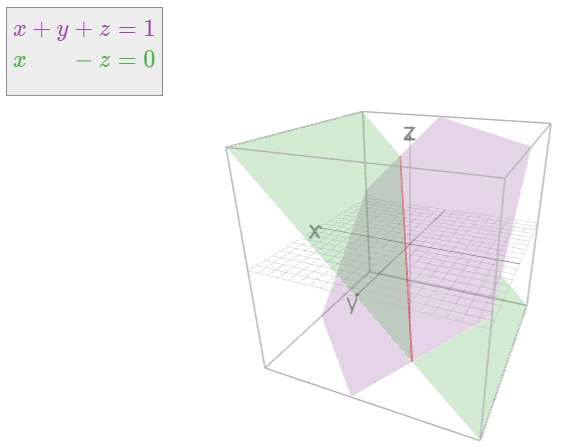
En general, las soluciones de un sistema de ecuaciones en\(n\) variables es la intersección de “\((n-1)\)-planos” en\(n\) -espacio. Este es siempre algún tipo de espacio lineal, como discutiremos en la Sección 2.4.
Descripción paramétrica de conjuntos de soluciones
De acuerdo con la Definición para Conjuntos de Soluciones, Definición\(\PageIndex{2}\), resolver un sistema de ecuaciones significa anotar todas las soluciones en términos de algún número de parámetros. Daremos una manera sistemática de hacerlo en la Sección 1.3; por ahora damos descripciones paramétricas en los ejemplos de la Subsección anterior, Imágenes de Conjuntos de Soluciones.
Considera la ecuación lineal\(x+y=1\) de Ejemplo\(\PageIndex{8}\). En este contexto, llamamos\(x+y=1\) una ecuación implícita de la línea. Podemos escribir la misma línea en forma paramétrica de la siguiente manera:
\[ (x, y) = (t,\, 1-t) \quad\text{for any}\quad t \in \mathbb{R}. \nonumber \]
Esto significa que cada punto de la línea tiene la forma\((t,\, 1-t)\) para algún número real\(t\). En este caso, llamamos a\(t\) un parámetro, ya que parametriza los puntos en la línea.
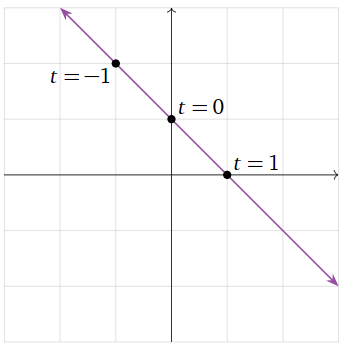
Figura\(\PageIndex{14}\)
Consideremos ahora el sistema de dos ecuaciones lineales
\[\left\{\begin{array}{rrrrr}\color{Violet}{x}&\color{Violet}{+}&\color{Violet}{y}&\color{Violet}{+}&\color{Violet}{z}&\color{Violet}{=}&\color{Violet}{1} \\ \color{Green}{x}&\color{Green}{}&\color{Green}{}&\color{Green}{-}&\color{Green}{z}&\color{Green}{=}&\color{Green}{0.}\end{array}\right.\nonumber\]
de Ejemplo\(\PageIndex{11}\). Estos forman colectivamente las ecuaciones implícitas para una línea en\(\mathbb{R}^3\). (Se necesitan al menos dos ecuaciones para definir una línea en el espacio). Esta línea también tiene una forma paramétrica con un parámetro\(t\text{:}\)
\[ (x,\, y,\, z) = (t,\, 1-2t,\, t). \nonumber \]
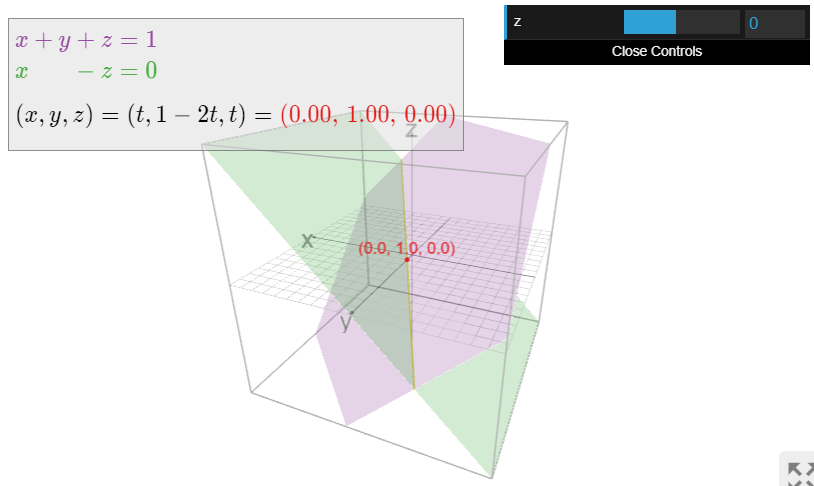
Tenga en cuenta que en cada caso, el parámetro nos\(t\) permite usar\(\mathbb{R}\) para etiquetar los puntos en la línea. Sin embargo, ninguna línea es igual que la recta numérica de\(\mathbb{R}\text{:}\) hecho, cada punto de la primera línea tiene dos coordenadas, como el punto\((0,1)\text{,}\) y cada punto de la segunda línea tiene tres coordenadas, como\((0,1,0)\).
Considera la ecuación lineal\(x+y+z=1\) de Ejemplo\(\PageIndex{9}\). Esta es una ecuación implícita de un plano en el espacio. Este plano tiene una ecuación en forma paramétrica: podemos escribir cada punto del plano como
\[ (x,\, y,\, z) = (1-t-w,\, t,\, w) \quad\text{for any}\quad t,w\in\mathbb{R}. \nonumber \]
En este caso, necesitamos dos parámetros\(t\) y\(w\) describir todos los puntos del plano.
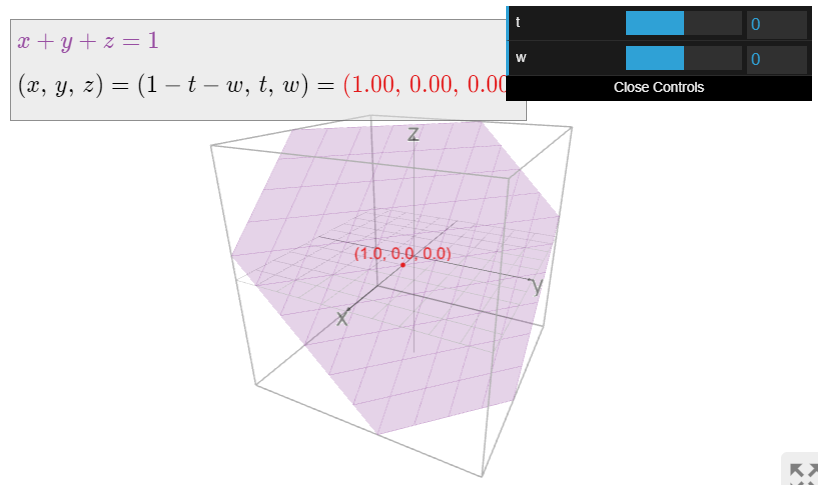
Tenga en cuenta que los parámetros nos\(t,w\) permiten usar\(\mathbb{R}^2\) para etiquetar los puntos en el plano. No obstante, este plano no es lo mismo que el plano de\(\mathbb{R}^2\text{:}\) hecho, cada punto de este plano tiene tres coordenadas, como el punto\((0,0,1)\).
Cuando hay una solución única, como en Ejemplo\(\PageIndex{10}\), no es necesario usar parámetros para describir el conjunto de soluciones.


