1.2: Reducción de filas
- Page ID
- 113119
- Aprender a reemplazar un sistema de ecuaciones lineales por una matriz aumentada.
- Aprenda cómo el método de eliminación corresponde a realizar operaciones de fila en una matriz aumentada.
- Entender cuándo una matriz está en forma de escalón de fila (reducida).
- Aprenda qué matrices reducidas de filas provienen de sistemas lineales inconsistentes.
- Receta: el algoritmo de reducción de filas.
- Palabras de vocabulario: operación de fila, equivalencia de fila, matriz, matriz aumentada, pivote, forma de escalón de fila (reducida).
En esta sección, presentaremos un algoritmo para “resolver” un sistema de ecuaciones lineales.
El método de eliminación
Resolveremos sistemas de ecuaciones lineales algebraicamente utilizando el método de eliminación. Es decir, combinaremos las ecuaciones de varias maneras para tratar de eliminar tantas variables como sea posible de cada ecuación. Hay tres operaciones válidas que podemos realizar en nuestro sistema de ecuaciones:
- Escalado: podemos multiplicar ambos lados de una ecuación por un número distinto de cero.
\[\left\{\begin{array}{rrrrrrr}x &+& 2y &+& 3z &=& 6\\ 2x &-& 3y &+& 2z &=& 14\\ 3x &+& y &-& z &=& -2\end{array}\right. \quad\xrightarrow{\text{multiply 1st by $-3$}}\quad \left\{\begin{array}{rrrrrrr} -3x &-& 6y &-& 9z &=& -18\\ 2x &-& 3y &+& 2z &=& 14\\ 3x &+& y &-& z &=& -2\end{array}\right. \nonumber \] - Reemplazo: podemos agregar un múltiplo de una ecuación a otra, reemplazando la segunda ecuación con el resultado.
\[\left\{\begin{array}{rrrrrrr}x &+& 2y &+& 3z &=& 6\\ 2x &-& 3y &+& 2z &=& 14\\ 3x &+& y &-& z &=& -2 \end{array}\right. \quad\xrightarrow{\text{2nd ${}={}$ 2nd$-2\times$1st}}\quad \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6\\ {}&{}& -7y &-& 4z &=& 2\\ 3x &+& y &-& z &=& -2\end{array}\right.\nonumber\] - Swap: podemos intercambiar dos ecuaciones.
\[\left\{\begin{array}{rrrrrrr}x &+& 2y &+& 3z &=& 6\\ 2x &-& 3y &+& 2z &=& 14\\ 3x &+& y &-& z &=& -2 \end{array}\right. \quad\xrightarrow{\text{3rd $\longleftrightarrow$ 1st}}\quad \left\{\begin{array}{rrrrrrr} 3x &+& y &-& z &=& -2\\ 2x &-& 3y &+& 2z &=& 14\\ x &+& 2y &+& 3z &=& 6\end{array}\right.\nonumber\]
Resolver Ecuación (1.1.1) usando el método de eliminación.
Solución
\[\begin{aligned} \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6\\ 2x &-& 3y &+& 2z &=& 14\\ 3x &+& y &-& z &=& -2\end{array}\right. \quad\xrightarrow{\text{2nd ${}={}$ 2nd$-2\times$1st}}\quad & \left\{\begin{array}{rrrrrrr}x &+& 2y &+& 3z &=& 6\\ {}&{}& -7y &-& 4z &=& 2\\ 3x &+& y &-& z &=& -2 \end{array}\right. \\ {} \quad\xrightarrow{\text{3rd ${}={}$ 3rd$-3\times$1st}}\quad& \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6 \\ {}&{}& -7y &-& 4z &=& 2\\ {}&{}& -5y &-& 10z &=& -20 \end{array}\right. \\ {} \quad\xrightarrow{\text{2nd $\longleftrightarrow$ 3rd}}\quad & \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6\\ {}&{}& -5y &-& 10z &=& -20 \\ {}&{}& -7y &-& 4z &=& 2\end{array}\right. \\ {} \quad\xrightarrow{\text{divide 2nd by $-5$}}\quad & \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6 \\ {}&{}& y &+& 2z &=& 4\\ {}&{}& -7y &-& 4z &=& 2 \end{array}\right. \\ {} \quad\xrightarrow{\text{3rd ${}={}$ 3rd$+7\times$2nd}}\quad & \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6\\ {}&{}&y &+& 2z &=& 4 \\ {}&{}&{}&{}&10z &=& 30 \end{array}\right.\end{aligned}\]
En este punto hemos eliminado ambos\(x\) y\(y\) de la tercera ecuación, y podemos resolver\(10z=30\) para conseguir\(z=3\). Sustituyendo\(z\) en la segunda ecuación da\(y+2\cdot3=4\text{,}\) o\(y=-2\). Sustituyendo\(y\) y\(z\) en la primera ecuación da\(x + 2\cdot(-2) + 3\cdot3 = 6\text{,}\) o\(x=3\). Así la única solución es\((x,y,z)=(1,-2,3)\).
Podemos comprobar que nuestra solución es correcta sustituyendo\((x,y,z)=(1,-2,3)\) en la ecuación original:
\[\left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6 \\ 2x &-& 3y &+& 2z &=& 14 \\ 3x &+& y &-& z &=& -2 \end{array}\right. \quad\xrightarrow{\text{substitute}}\quad \left\{\begin{array}{rrrrrrr} 1 &2&\cdot(-2) &+& 3\cdot 3 &=& 6 \\ 2\cdot 1 &-& 3\cdot(-2) &+& 2\cdot 3 &=& 14 \\ 3\cdot 1 &+& (-2) &-& 3 &=& -2 \end{array}\right. \nonumber\]
Matrices Aumentadas y Operaciones de Fila
Resolver ecuaciones por eliminación requiere escribir las variables\(x,y,z\) y los iguales firman una y\(=\) otra vez, simplemente como marcadores de posición: todo lo que está cambiando en las ecuaciones son los números de coeficientes. Podemos hacer nuestra vida más fácil extrayendo solo los números, y poniéndolos en una caja:
\[\left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6\\ 2x &-& 3y &+& 2z& =& 14\\ 3x &+& y &-& z &=& -2\end{array}\right. \quad\xrightarrow{\text{becomes}}\quad \left(\begin{array}{ccc|c} 1&2&3&6 \\ 2&-3&2&14 \\ 3&1&-1&-2 \end{array}\right).\nonumber\]
A esto se le llama matriz aumentada. La palabra “aumentada” se refiere a la línea vertical, que dibujamos para recordarnos a dónde pertenece el signo igual; una matriz es una cuadrícula de números sin la línea vertical. En esta notación, nuestras tres formas válidas de manipular nuestras ecuaciones se convierten en operaciones de fila:
- Escalado: multiplica todas las entradas en una fila por un número distinto de cero.
\[\left(\begin{array}{ccc|c} 1& 2& 3& 6&\\ 2& -3& 2& 14\\ 3& 1& -1& -2\end{array}\right) \quad\xrightarrow{R_1 = R_1 \times -3}\quad \left(\begin{array}{ccc|c} -3 &-6 &-9 &-18\\ 2& -3& 2& 14\\ 3& 1& -1& -2\end{array}\right)\nonumber\]
Aquí la notación\(R_1\) simplemente significa “la primera fila”, e igualmente para\(R_2,R_3,\) etc. - Reemplazo: agregar un múltiplo de una fila a otra, reemplazando la segunda fila con el resultado.
\[\left(\begin{array}{ccc|c}1 &2& 3& 6\\ 2& -3& 2& 14\\ 3& 1& -1& -2\end{array}\right) \quad\xrightarrow{R_2 = R_2 -2\times R_1}\quad \left(\begin{array}{ccc|c} 1 &2 &3 &6 \\ 0& -7& -4& 2\\ 3& 1& -1& -2\end{array}\right)\nonumber\] - Swap: intercambiar dos filas.
\[\left(\begin{array}{ccc|c} 1 &2 &3 &6 \\ 2& -3& 2& 14\\ 3& 1& -1& -2\end{array}\right) \quad\xrightarrow{R_1 \longleftrightarrow R_3}\quad \left(\begin{array}{ccc|c} 3 &1 &-1& -2\\ 2& -3& 2& 14\\ 1& 2& 3& 6\end{array}\right)\nonumber\]
Cuando escribimos nuestras operaciones de fila arriba usamos expresiones como\(R_2 = R_2 - 2 \times R_1\). Por supuesto esto no quiere decir que la segunda fila sea igual a la segunda fila menos el doble de la primera fila. En cambio significa que estamos reemplazando la segunda fila por la segunda fila menos el doble de la primera fila. Este tipo de sintaxis se usa frecuentemente en la programación informática cuando queremos cambiar el valor de una variable.
Resolver Ecuación (1.1.1) usando operaciones de fila.
Solución
Comenzamos formando una matriz aumentada:
\[\left\{\begin{array}{rrrrrrr} x&+&2y&+&3x&=& 6\\ 2x&-&3y&+&2z&=&14 \\ 3x&+&y&-&z&=&-2 \end{array}\right. \quad\xrightarrow{\text{becomes}}\quad \left(\begin{array}{ccc|c}1&2&3&6\\2&-3&2&14\\3&1&-1&-2\end{array}\right).\nonumber \]
Eliminar una variable de una ecuación significa producir un cero a la izquierda de la línea en una matriz aumentada. Primero producimos ceros en la primera columna (es decir, eliminamos\(x\)) restando múltiplos de la primera fila.
\[\begin{aligned} \left(\begin{array}{ccc|c} 1 &2 &3& 6\\ 2& -3& 2& 14\\ 3& 1& -1& -2\end{array}\right) & \quad\xrightarrow{R_2=R_2-2R_1}\quad \left(\begin{array}{ccc|c} 1 &2 &3& 6\\ \color{red}{0}& -7& -4& 2\\ 3& 1& -1& -2\end{array}\right) \\ & \quad\xrightarrow{R_3=R_3-3R_1}\quad \left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& -7& -4& 2\\ \color{red}{0}& -5& -10& -20\end{array}\right) \end{aligned}\]
Esto se hizo mucho más fácil por el hecho de que la entrada superior izquierda es igual a\(1\text{,}\) así que simplemente podemos multiplicar la primera fila por el número de abajo y restar. Para eliminar de\(y\) la misma manera, nos gustaría producir un\(1\) en la segunda columna. Podríamos dividir la segunda fila por\(-7\text{,}\) pero esto produciría fracciones; en cambio, dividamos la tercera por\(-5\).
\[\begin{aligned} \left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& -7& -4& 2\\ 0& -5& -10& -20 \end{array}\right) \quad\xrightarrow{R_3=R_3\div-5}\quad & \left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0 &-7& -4& 2\\ 0& \color{red}{1}& 2& 4\end{array}\right) \\ {}\quad\xrightarrow{R_2\longleftrightarrow R_3}\quad & \left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& 1& 2& 4 \\ 0& -7& -4& 2\end{array}\right) \\ {}\quad\xrightarrow{R_3 = R_3+7R_2}\quad & \left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& 1& 2& 4\\ 0& \color{red}{0} & 10& 30 \end{array}\right) \\ {}\quad\xrightarrow{R_3 = R_3\div 10}\quad & \left(\begin{array}{ccc|c}1 &2& 3& 6\\ 0& 1& 2& 4 \\ 0& 0& \color{red}{1}& 3\end{array}\right)\end{aligned}\]
Cambiamos la segunda y tercera fila sólo para mantener las cosas ordenadas. Ahora traducimos esta matriz aumentada de nuevo en un sistema de ecuaciones:
\[\left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& 1& 2& 4\\ 0& 0& 1& 3\end{array}\right) \quad\xrightarrow{\text{becomes}}\quad \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6 \\ {}&{}& y &+& 2z &=& 4 \\ {}&{}&{}&{}&z &=& 3\end{array}\right.\nonumber \]
Por lo\(z=3\text{;}\) tanto, la sustitución inversa como en el Ejemplo\(\PageIndex{1}\) da\((x,y,z)=(1,-2,3)\).
¡El proceso de hacer operaciones de fila a una matriz no cambia el conjunto de soluciones de las ecuaciones lineales correspondientes!
En efecto, el objetivo de hacer estas operaciones es resolver las ecuaciones utilizando el método de eliminación.
Dos matrices se denominan equivalentes de fila si una se puede obtener de la otra haciendo cierto número de operaciones de fila.
Entonces las ecuaciones lineales de matrices equivalentes a filas tienen el mismo conjunto de soluciones.
Resuelva el siguiente sistema de ecuaciones mediante operaciones de fila:
\[\left\{\begin{array}{rrrrr} x &+& y& =& 2\\ 3x &+& 4y &=& 5\\ 4x &+ &5y &=& 9\end{array}\right. \nonumber\]
Solución
Primero ponemos nuestro sistema de ecuaciones en una matriz aumentada.
\[\left\{\begin{array}{rrrrr} x &+& y &=& 2\\ 3x &+& 4y &=& 5\\ 4x &+& 5y &=& 9\end{array}\right. \quad\xrightarrow{\text{augmented matrix}}\quad \left(\begin{array}{cc|c} 1 &1& 2\\ 3 &4& 5\\ 4& 5& 9\end{array}\right) \nonumber\]
Borramos las entradas debajo de la parte superior izquierda usando el reemplazo de filas.
\[\begin{aligned}\left(\begin{array}{cc|c} 1 &1& 2\\ 3& 4& 5\\ 4& 5& 9\end{array}\right) \quad\xrightarrow{R_2=R_2-3R_1}\quad & \left(\begin{array}{cc|c} 1 &1& 2\\ \color{red}{0} & 1& -1\\ 4& 5& 9\end{array}\right) \\ {} \quad\xrightarrow{R_3=R_3-4R_1}\quad & \left(\begin{array}{cc|c} 1 &1& 2\\ 0& 1& -1\\ \color{red}{0}& 1& 1\end{array}\right)\end{aligned}\]
Ahora despejamos la segunda entrada de la última fila.
\[\left(\begin{array}{cc|c} 1 &1& 2\\ 0& 1& -1\\ 0 &1& 1\end{array}\right) \quad\xrightarrow{R_3=R_3-R_2}\quad \left(\begin{array}{cc|c} 1 &1& 2\\ 0& 1& -1\\ 0& \color{red}{0}& 2\end{array}\right) \nonumber \]
Esto se traduce de nuevo en el sistema de ecuaciones
\[\left\{\begin{array}{rrrrr} x &+& y &=& 2\\ {}&{}& y& =& -1 \\ {}&{}& 0& =& 2. \end{array}\right. \nonumber\]
Nuestro sistema original tiene el mismo conjunto de soluciones que este sistema. Pero este sistema no tiene soluciones: ¡no hay valores de\(x,y\) hacer verdadera la tercera ecuación! Concluimos que nuestra ecuación original era inconsistente.
Formularios Echelon
En la anterior Subsección El Método de Eliminación vimos cómo traducir un sistema de ecuaciones lineales en una matriz aumentada. Queremos encontrar un algoritmo para “resolver” tal matriz aumentada. Primero debemos decidir qué significa que una matriz aumentada sea “resuelta”.
Una matriz está en forma de escalón de filas si:
- Todas las filas cero están en la parte inferior.
- La primera entrada distinta de cero de una fila está a la derecha de la primera entrada distinta de cero de la fila anterior.
- Por debajo de la primera entrada distinta de cero de una fila, todas las entradas son cero.
Aquí hay una imagen de una matriz en forma de escalón de fila:
\[\left(\begin{array}{ccccc} \color{red}{\boxed{\star}} &\star &\star &\star &\star \\ 0&\color{red}{\boxed{\star}} & \star &\star &\star \\ 0&0&0&\color{red}{\boxed{\star}} &\star \\ 0&0&0&0&0 \end{array}\right) \qquad \begin{aligned} \star &= \text{any number} \\ \color{red}\boxed\star &= \text{any nonzero number} \end{aligned} \nonumber \]
Un pivote es la primera entrada distinta de cero de una fila de una matriz en forma de escalón de fila.
Una matriz en forma de fila escalonada es generalmente fácil de resolver usando la sustitución inversa. Por ejemplo,
\[\left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& 1& 2& 4 \\ 0& 0& 10& 30 \end{array}\right) \quad\xrightarrow{\text{becomes}}\quad \left\{\begin{array}{rrrrrrr} x &+& 2y &+& 3z &=& 6 \\ {}&{}& y &+& 2z& =& 4 \\ {}&{}&{}&{}& 10z &=& 30. \end{array}\right. \nonumber\]
De inmediato vemos\(z=3\text{,}\) lo que implica\(y = 4-2\cdot 3 = -2\) y\(x = 6 - 2(-2) - 3\cdot 3 = 1.\) Ver Ejemplo\(\PageIndex{3}\).
Una matriz está en forma de escalón de fila reducida si está en forma de escalón de fila, y además:
- Cada pivote es igual a 1.
- Cada pivote es la única entrada distinta de cero en su columna.
Aquí hay una imagen de una matriz en forma de escalón de fila reducida:
\[\left(\begin{array}{ccccc} \color{red}{1} &0&\star &0&\star \\ 0&\color{red}{1} &\star &0 &\star \\ 0&0&0&\color{red}{1}&\star \\ 0&0&0&0&0\end{array}\right) \qquad \begin{aligned} \star &= \text{any number} \\ \color{red}1 &= \text{pivot} \end{aligned} \nonumber\]
Una matriz en forma de escalón de fila reducida está en cierto sentido completamente resuelta. Por ejemplo,
\[\left(\begin{array}{ccc|c} 1 &0& 0& 1\\ 0& 1& 0& -2\\ 0& 0& 1& 3\end{array}\right) \quad\xrightarrow{\text{becomes}}\quad \left\{\begin{array}{rrr} x &=& 1\\ y &=& -2 \\ z &=& 3.\end{array}\right. \nonumber \]
Las siguientes matrices están en forma de escalón de fila reducida:
\[\left(\begin{array}{ccc}1&0&2 \\ 0&1&-1\end{array}\right)\qquad \left(\begin{array}{cccc}0&1&8&0\end{array}\right) \qquad \left(\begin{array}{cc|c} 1&17&0\\0&0&1\end{array}\right)\qquad\left(\begin{array}{ccc}0&0&0\\0&0&0\end{array}\right).\nonumber\]
Las siguientes matrices están en forma de escalón de fila pero no en forma de escalón de fila reducida:
\[\left(\begin{array}{cc}2&1\\0&1\end{array}\right)\qquad \left(\begin{array}{ccc|c} 2&7&1&4 \\ 0&0&2&1 \\ 0&0&0&3\end{array}\right)\qquad \left(\begin{array}{ccc}1&17&0\\0&1&1\end{array}\right) \qquad \left(\begin{array}{ccc}2&1&3\\0&0&0\end{array}\right).\nonumber\]
Las siguientes matrices no están en forma escalón:
\[\left(\begin{array}{ccc|c} 2&7&1&4\\0&0&2&1\\0&0&1&3 \end{array}\right)\qquad\left(\begin{array}{cc|c}0&17&0\\0&2&1\end{array}\right)\qquad\left(\begin{array}{cc}2&1\\2&1\end{array}\right) \qquad \left(\begin{array}{c}0\\1\\0\\0\end{array}\right).\nonumber\]
Al decidir si una matriz aumentada está en forma de escalón de fila (reducida), no hay nada especial en las columnas aumentadas. Simplemente ignore la línea vertical.
Si una matriz aumentada está en forma de escalón de fila reducida, el sistema lineal correspondiente se considera resuelto. A continuación veremos por qué este es el caso, y mostraremos que cualquier matriz se puede poner en forma de escalón de fila reducida usando solo operaciones de fila.
Considere el siguiente sistema de ecuaciones:
\[\left\{\begin{array}{rrrrr}x &-& y &=& 0\\ x &+& y &=& 2.\end{array}\right.\nonumber\]
Podemos visualizar este sistema como un par de líneas en\(\mathbb{R}^2\) (rojo y azul, respectivamente, en la imagen de abajo) que se cruzan en el punto\((1,1)\). Si restamos la primera ecuación de la segunda, obtenemos la ecuación\(2y=2\text{,}\) o\(y=1\). Esto da como resultado el sistema de ecuaciones:
\[\left\{\begin{array}{rrrrr}x &-& y &=& 0 \\ {}&{} &y &=& 1.\end{array}\right.\nonumber\]
En términos de operaciones de fila en matrices, podemos escribir esto como:
\[\begin{aligned} \left(\begin{array}{cc|c} 1&-1&0 \\ 1&1&2\end{array}\right) \quad\xrightarrow{R_2=R_2-R_1}\quad & \left(\begin{array}{cc|c} 1&-1&0 \\ 0&2&2\end{array}\right) \\ {} \quad\xrightarrow{R_2=\frac{1}{2}R_2}\quad & \left(\begin{array}{cc|c} 1&-1&0\\0&1&1\end{array}\right)\end{aligned}\]
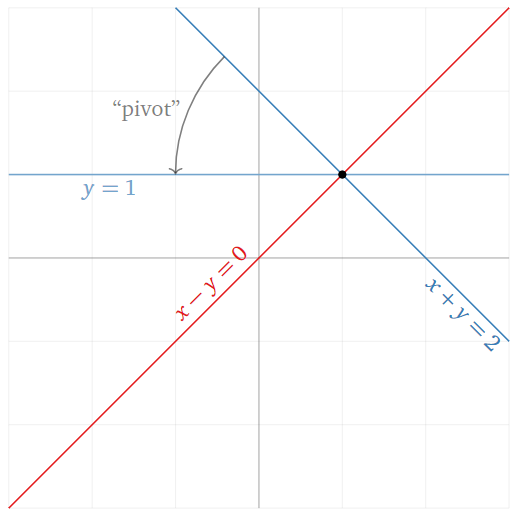
Figura\(\PageIndex{1}\)
Lo que ha ocurrido geométricamente es que la línea azul original ha sido reemplazada por la nueva línea azul\(y=1\). Podemos pensar en la línea azul como giratoria, o pivotante, alrededor de la solución\((1,1)\). Utilizamos la posición de pivote en la matriz para hacer que la línea azul pivote así. Esta es una posible explicación para la terminología “pivote”.
El algoritmo de reducción de filas
Cada matriz es fila equivalente a una y sólo una matriz en forma de escalón de fila reducida.
Daremos un algoritmo, llamado reducción de fila o eliminación gaussiana, que demuestra que cada matriz es fila equivalente a al menos una matriz en forma de escalón de fila reducida.
La declaración de singularidad es interesante, significa que, no importa cómo reduzcas las filas, siempre obtienes la misma matriz en forma de escalón de fila reducida.
Esto supone, por supuesto, que solo haces las tres operaciones legales de fila, y no cometes ningún error aritmético.
No vamos a demostrar singularidad, ¡pero tal vez usted pueda!
- Paso 1a: Intercambia la 1ª fila por una inferior para que una entrada más a la izquierda distinta de cero esté en la 1ª fila (si es necesario).
- Paso 1b: Escala la 1ª fila para que su primera entrada distinta de cero sea igual a 1.
- Paso 1c: Use el reemplazo de fila para que todas las entradas debajo de este 1 sean 0.
- Paso 2a: Intercambia la 2da fila por una inferior para que la entrada más a la izquierda distinta de cero esté en la 2da fila.
- Paso 2b: Escala la 2da fila para que su primera entrada distinta de cero sea igual a 1.
- Paso 2c: Use el reemplazo de fila para que todas las entradas debajo de este 1 sean 0.
- Paso 3a: Intercambia la 3ª fila por una inferior para que la entrada más a la izquierda distinta de cero esté en la 3ª fila.
- etc.
- Último Paso: Use el reemplazo de fila para borrar todas las entradas por encima de los pivotes, comenzando por el último pivote.
Fila reduce esta matriz:
\[\left(\begin{array}{ccc|c} 0&-7&-4&2 \\ 2&4&6&12\\ 3&1&-1&-2\end{array}\right).\nonumber\]
Solución


La forma de escalón de fila reducida de la matriz es
\[\left(\begin{array}{ccc|c}1&0&0&1 \\ 0&1&0&-2\\0&0&1&3\end{array}\right) \quad\xrightarrow{\text{translates to}}\quad \left\{\begin{array}{rrrrrrr} x&{}&{}&{}&{}&=&1 \\ {}&{}&y&{}&{}&=&-2 \\ {}&{}&{}&{}&z&=&3.\end{array}\right.\nonumber\]
La forma de escalón de fila reducida de la matriz nos dice que la única solución es\((x,y,z) = (1,-2,3).\)
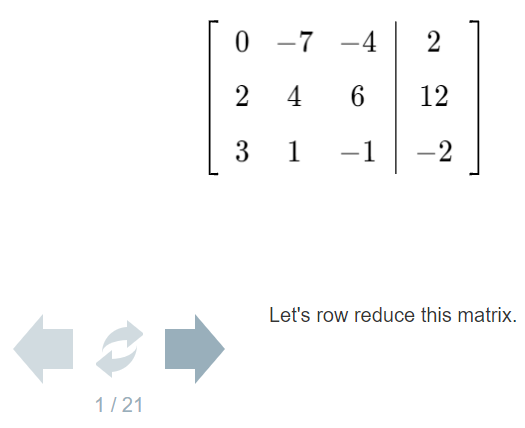
Aquí está el algoritmo de reducción de filas, resumido en imágenes.

Figura\(\PageIndex{3}\)
Será muy importante saber dónde están los pivotes de una matriz después de la reducción de filas; esta es la razón de la siguiente pieza terminológica.
Una posición de pivote de una matriz es una entrada que es un pivote de una forma de escalón de fila de esa matriz.
Una columna de pivote de una matriz es una columna que contiene una posición de pivote.
Encuentra las posiciones de pivote y las columnas de pivote de esta matriz
\[A=\left(\begin{array}{ccc|c} 0 &-7& -4& 2\\ 2& 4& 6& 12 \\ 3& 1& -1& -2\end{array}\right).\nonumber\]
Solución
Vimos en Ejemplo\(\PageIndex{5}\) que una fila escalón forma de la matriz es
\[\left(\begin{array}{ccc|c} 1 &2& 3& 6\\ 0& 1& 2& 4\\ 0& 0& 10& 30\end{array}\right).\nonumber\]
Las posiciones de pivote de\(A\) son las entradas que se convierten en pivotes en forma de escalón de fila; están marcadas en rojo a continuación:
\[\left(\begin{array}{ccc|c}\color{red}{0}&-7&-4&2 \\ 2&\color{red}{4}&6&12 \\ 3&1&\color{red}{-1}&-2\end{array}\right).\nonumber\]
La primera, segunda y tercera columnas son columnas pivotes.
Resolver el sistema lineal
\[\left\{\begin{array}{rrrrr}2x &+& 10y &=& -1 \\ 3x &+& 15y &=& 2\end{array}\right. \nonumber \]
usando reducción de filas.
Solución
\[\begin{aligned} \left(\begin{array}{cc|c} 2&10&-1 \\ 3&15&2 \end{array}\right) \quad\xrightarrow{R_1=R_1\div 2}\quad & \left(\begin{array}{cc|c} \color{red}{1}&5&{-\frac{1}{2}} \\ 3&15&2 \end{array}\right) &&\color{blue}{\text{(Step 1b)}} \\ {} \quad\xrightarrow{R_2=R_2-3R_1}\quad & \left(\begin{array}{cc|c} 1&5&{-\frac{1}{2}} \\ \color{red}{0} &0&{\frac{7}{2}} \end{array}\right) &&\color{blue}{\text{(Step 1c)}} \\ {}\quad\xrightarrow{R_2=R_2\times\frac 27}\quad & \left(\begin{array}{cc|c} 1&5&{-\frac{1}{2}} \\ 0&0&\color{red}{1} \end{array}\right) &&\color{blue}{\text{(Step 2b)}} \\ {} \quad\xrightarrow{R_1=R_1+\frac 12R_2}\quad & \left(\begin{array}{cc|c} 1&5&\color{red}{0} \\ 0&0&1\end{array}\right) &&\color{blue}{\text{(Step 2c)}}\end{aligned}\]
Esta matriz de fila reducida corresponde al sistema inconsistente
\[\left\{\begin{array}{rrrrr} x &+& 5y &=& 0\\ {}&{}&0& =& 1. \end{array}\right. \nonumber \]
En el ejemplo anterior, vimos cómo reconocer la forma de escalón de fila reducida de un sistema inconsistente.
Una matriz aumentada corresponde a un sistema inconsistente de ecuaciones si y solo si la última columna (es decir, la columna aumentada) es una columna pivotante.
En otras palabras, la matriz de fila reducida de un sistema inconsistente se ve así:
\[\left(\begin{array}{cccc|c} 1&0&\star &\star &\color{red}{0} \\ 0&1&\star &\star &\color{red}{0}\\ 0&0&0&0&\color{red}{1}\end{array}\right)\nonumber\]
Hasta el momento hemos discutido dos clases de matrices:
- Cuando la forma de escalón de fila reducida de una matriz tiene un pivote en cada columna no aumentada, entonces corresponde a un sistema con una solución única:
\[\left(\begin{array}{ccc|c} 1 &0& 0& 1\\ 0& 1& 0& -2\\ 0& 0& 1& 3\end{array}\right) \quad\xrightarrow{\text{translates to}}\quad \left\{\begin{array}{rrrrrrc} x&{}&{}&{}&{}&=&1 \\ {}&{}&y&{}&{}&=&-2 \\ {}&{}&{}&{}&z&=&3.\end{array}\right. \nonumber\] - Cuando la forma de escalón de fila reducida de una matriz tiene un pivote en la última columna (aumentada), entonces corresponde a un sistema sin soluciones:
\[\left(\begin{array}{cc|c} 1&5&0 \\ 0&0&1\end{array}\right) \quad\xrightarrow{\text{translates to}}\quad \left\{\begin{array}{rrrrrrl} x &+& 5y &=& 0 \\ {}&{}& 0 &=& 1.\end{array}\right.\nonumber\]
¿Qué sucede cuando una de las columnas no aumentadas carece de pivote? Este es el tema de la Sección 1.3.
Resolver el sistema lineal
\[\left\{\begin{array}{rrrrrrr}2x &+& y &+& 12z &=& 1\\ x &+& 2y &+& 9z &=& -1\end{array}\right. \nonumber\]
usando reducción de filas.
Solución
\[\begin{aligned} \left(\begin{array}{ccc|c} 2&1&12&1 \\ 1&2&9&-1\end{array}\right) \quad\xrightarrow{R_1 \longleftrightarrow R_2}\quad & \left(\begin{array}{ccc|c} \color{red}{1} &2&9&-1 \\ 2&1&12&1 \end{array}\right) &&\color{blue}{\text{(Optional)}} \\ {}\quad\xrightarrow{R_2=R_2-2R_1}\quad & \left(\begin{array}{ccc|c} 1&2&9&-1 \\ \color{red}{0}&-3&-6&3 \end{array}\right) &&\color{blue}{\text{(Step 1c)}} \\ {} \quad\xrightarrow{R_2=R_2\div -3}\quad & \left(\begin{array}{ccc|c} 1&2&9&-1 \\ 0&\color{red}{1} &2&-1 \end{array}\right) &&\color{blue}{\text{(Step 2b)}} \\ {}\quad\xrightarrow{R_1=R_1-2R_2}\quad & \left(\begin{array}{ccc|c} 1&\color{red}{0}&5&1 \\ 0&1&2&-1\end{array}\right) &&\color{blue}{\text{(Step 2c)}}\end{aligned}\]
Esta matriz de fila reducida corresponde al sistema lineal
\[\left\{\begin{array}{rrrrc} x &+& 5z &=& 1 \\ y &+& 2z &=& -1\end{array}\right. \nonumber\]
¿En qué sentido está resuelto el sistema? Veremos en la Sección 1.3.


