2.8: Bases como sistemas de coordenadas
- Page ID
- 113050
- Aprende a ver una base como un sistema de coordenadas en un subespacio.
- Recetas: computar las\(\mathcal{B}\) coordenadas de un vector, computar las coordenadas habituales de un vector a partir\(\mathcal{B}\) de sus coordenadas.
- Imagen: las\(\mathcal{B}\) coordenadas -de un vector usando su ubicación en una cuadrícula de coordenadas no estándar.
- Vocabulario palabra:\(\mathcal{B}\) -coordenadas.
En esta sección, interpretamos una base de un subespacio\(V\) como un sistema de coordenadas sobre\(V\), y aprendemos a escribir un vector\(V\) en ese sistema de coordenadas.
Si\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\) es una base para un subespacio\(V\), entonces cualquier vector\(x\)\(V\) puede escribirse como una combinación lineal
\[x=c_1v_1+c_2v_2+\cdots +c_mv_m\nonumber\]
exactamente de una manera.
- Prueba
-
Recordemos que decir\(\mathcal{B}\) es una base para\(V\) medios que\(\mathcal{B}\) abarca\(V\) y\(\mathcal{B}\) es linealmente independiente. Desde\(\mathcal{B}\) abarca\(V\), podemos escribir cualquiera\(x\) en\(V\) como una combinación lineal de\(v_1,\: v_2,\cdots ,v_m\). Por singularidad, supongamos que teníamos dos expresiones de este tipo:
\[\begin{aligned}x&=c_1v_1+c_2v_2+\cdots +c_mv_m \\ x&=c_1'v_1+c_2'v_2+\cdots +c_m'v_m.\end{aligned}\]
Restar la primera ecuación de los segundos rendimientos
\[0=x-x=(c_1-c_1')v_1 +(c_2-c_2')v_2+\cdots +(c_m-c_m')v_m.\nonumber\]
Dado que\(\mathcal{B}\) es linealmente independiente, la única solución a la ecuación anterior es la solución trivial: todos los coeficientes deben ser cero. De ello se deduce que\(c_i−c_i'\) para todos\(i\), lo que lo demuestra\(c_1=c_1',\: c_2=c_2',\cdots ,c_m=c_m'\).
Considere las bases estándar\(\mathbb{R}^{3}\) del Ejemplo 2.7.3 en la Sección 2.7.
\[e_1=\left(\begin{array}{c}1\\0\\0\end{array}\right),\quad e_2=\left(\begin{array}{c}0\\1\\0\end{array}\right),\quad e_3=\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
De acuerdo con el hecho anterior,\(\PageIndex{1}\) Fact, cada vector en\(\mathbb{R}^{3}\) puede escribirse como una combinación lineal de\(e_1\),\(e_2\),\(e_3\), con coeficientes únicos. Por ejemplo,
\[v=\left(\begin{array}{c}\color{Red}{3}\\ \color{blue}{5} \\ \color{Green}{-2}\end{array}\right)\color{black}{=}\color{red}{3}\color{black}{\left(\begin{array}{c}1\\0\\0\end{array}\right)+}\color{blue}{5}\color{black}{\left(\begin{array}{c}0\\1\\0\end{array}\right)}\color{Green}{-2}\color{black}{\left(\begin{array}{c}0\\0\\1\end{array}\right)=}\color{Red}{3}\color{black}{e_1+}\color{blue}{5}\color{black}{e_2}\color{Green}{-2}\color{black}{e_3.}\nonumber\]
En este caso, las coordenadas de\(v\) son exactamente los coeficientes de\(e_1\),\(e_2\),\(e_3\).
¿Qué son exactamente las coordenadas, de todos modos? Una forma de pensar en las coordenadas es que dan indicaciones de cómo llegar a cierto punto desde el origen. En el ejemplo anterior, la combinación lineal\(3e_1+5e_2−2e_3\) puede ser pensada como la siguiente lista de instrucciones: iniciar en el origen, unidades de viaje al norte, luego\(3\) unidades de viaje\(5\) al este, luego\(2\) unidades hacia abajo.
Dejar\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\) ser una base de un subespacio\(V\), y dejar
\[x=c_1v_1+c_2v_2+\cdots+c_mv_m\nonumber\]
ser un vector en\(V\). Los coeficientes\(c_1,\:c_2,\cdots,c_m\) son las coordenadas de\(x\) con respecto a\(\mathcal{B}\). El vector\(\mathcal{B}\) -coordenada de\(x\) es el vector
\[[x]_{\mathcal{B}}=\left(\begin{array}{c}c_1 \\c_2\\ \vdots \\ c_m\end{array}\right)\quad\text{ in }\mathbb{R}^{m}.\nonumber\]
Si cambiamos la base, entonces todavía podemos dar instrucciones de cómo llegar al punto\((3,\:5,\:−2)\), pero las instrucciones serán diferentes. Digamos, por ejemplo, tomamos la base
\[v_1=e_1+e_2=\left(\begin{array}{c}1\\1\\0\end{array}\right),\quad v_2=e_2=\left(\begin{array}{c}0\\1\\0\end{array}\right),\quad v_3=e_3=\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
Podemos escribir\((3,\:5,\:−2)\) en esta base como\(3v_1+2v_2−2v_3\). En otras palabras: comenzar en el origen, viajar\(3\) tiempos hacia el noreste hasta\(v_1\), luego\(2\) unidades al este, luego\(2\) unidades hacia abajo. En esta situación, podemos decir que “\(3\)es la\(v_1\) -coordenada de\((3,\:5,\:−2)\),\(2\) es la\(v_2\) -coordenada de\((3,\:5,\:−2)\), y\(−2\) es la\(v_3\) -coordenada de”\((3,\:5,\:−2)\).
La definición anterior, Definición\(\PageIndex{1}\), da una manera de usar\(\mathbb{R}_m\) para etiquetar los puntos de un subespacio de dimensión\(m\): un punto es simplemente etiquetado por su vector\(\mathcal{B}\) -coordenada. Por ejemplo, si elegimos una base para un plano, podemos etiquetar los puntos de ese plano con los puntos de\(\mathbb{R}^2\).
Definir
\[v_1=\left(\begin{array}{c}1\\1\end{array}\right),\quad v_2=\left(\begin{array}{c}1\\-1\end{array}\right),\quad\mathcal{B}=\{v_1,\:v_2\}.\nonumber\]
- Verificar que\(\mathcal{B}\) sea una base para\(\mathbb{R}^2\).
- Si\([w]_{\mathcal{B}}=\left(\begin{array}{c}1\\2\end{array}\right)\), entonces ¿qué es\(w\)?
- Encuentra las\(\mathcal{B}\) coordenadas de\(v=\left(\begin{array}{c}5\\3\end{array}\right)\).
Solución
- Por el teorema de base en la Sección 2.7, Teorema 2.7.3, cualesquiera dos vectores linealmente independientes forman una base para\(\mathbb{R}^2\). Claramente no\(v_1,\:v_2\) son múltiplos entre sí, por lo que son linealmente independientes.
- Decir\([w]_{\mathcal{B}}=\left(\begin{array}{c}1\\2\end{array}\right)\) significa que\(1\) es la\(v_1\) coordenada de\(w\), y esa\(2\) es la\(v_2\) -coordenada:
\[w=v_1+2v_2=\left(\begin{array}{c}1\\1\end{array}\right)+2\left(\begin{array}{c}1\\-1\end{array}\right)=\left(\begin{array}{c}3\\-1\end{array}\right).\nonumber\] - Tenemos que resolver la ecuación vectorial\(v=c_1v_1+c_2v_2\) en las incógnitas\(c_1,\: c_2\). Formamos una matriz aumentada y la fila
\[\left(\begin{array}{cc|c} 1&1&5 \\ 1&-1&3\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad\left(\begin{array}{cc|c} 1&0&4 \\ 0&1&1\end{array}\right).\nonumber\]
reducimos: Tenemos\(c_1=4\) y\(c_2=1\), así\(v=4v_1+v_2\) y\([v]_{\mathcal{B}}=\left(\begin{array}{c}4\\1\end{array}\right)\).
En la siguiente imagen, indicamos el sistema de coordenadas definido\(\mathcal{B}\) por trazando líneas paralelas al “\(v_1\)-axis” y “\(v_2\)-axis”. Usando esta cuadrícula es fácil ver que las\(\mathcal{B}\) -coordenadas de\(v\) son\(\left(\begin{array}{c}5\\1\end{array}\right)\), y que las\(\mathcal{B}\) -coordenadas de\(w\) son\(\left(\begin{array}{c}1\\2\end{array}\right)\).
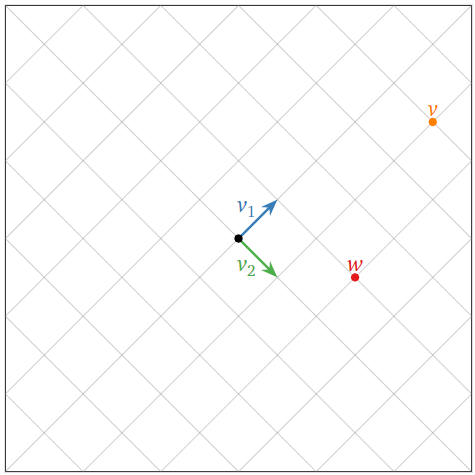
Figura\(\PageIndex{1}\)
Esta imagen podría ser la cuadrícula de calles en Palo Alto, California. Los residentes de Palo Alto se refieren al noroeste como “norte” y al noreste como “este”. Hay una razón para ello: el viejo camino a San Francisco se llama El Camino Real, y ese camino corre de sureste a noroeste en Palo Alto. Entonces, cuando un residente de Palo Alto dice “ir al sur dos cuadras y al este una cuadra”, están dando indicaciones desde el origen hasta el Whole Foods en\(w\).
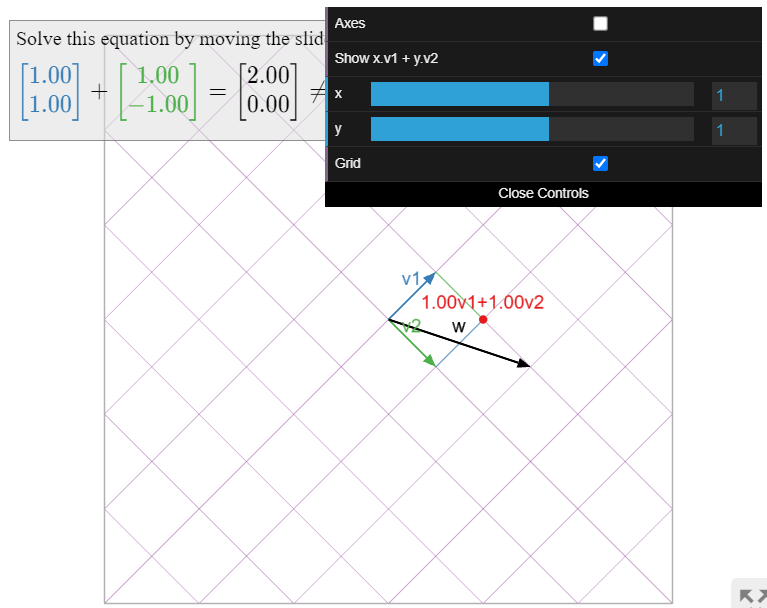
Figura\(\PageIndex{2}\): Una imagen de la base\(\mathcal{B}=\{v_1,\: v_2\}\) de\(\mathbb{R}^2\). La cuadrícula indica el sistema de coordenadas definido por la base\(\mathcal{B}\); un conjunto de líneas mide la\(v_1\) coordenada y el otro conjunto mide la\(v_2\) coordenada. Utilice los controles deslizantes para encontrar las\(\mathcal{B}\) coordenadas -de\(w\).
Let
\[v_1=\left(\begin{array}{c}2\\-1\\1\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\0\\-1\end{array}\right).\nonumber\]
Estos forman una base\(\mathcal{B}\) para un avión\(V=\text{Span}\{v_1,\: v_2\}\) en\(\mathbb{R}^3\). Indicamos el sistema de coordenadas definido\(\mathcal{B}\) por trazando líneas paralelas al “\(v_1\)eje -axis” y “\(v_2\)-axis”:
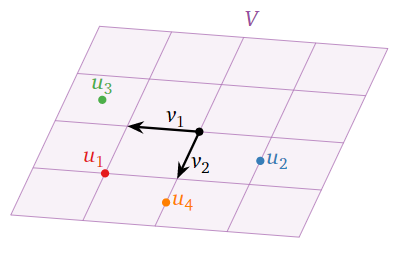
Figura\(\PageIndex{3}\)
Podemos ver a partir de la imagen que la\(v_1\) coordenada -de\(\color{red}{u_1}\) es igual a\(1\), como es la\(v_2\) -coordenada, entonces\([\color{red}{u_1}\color{black}{]_{\mathcal{B}}=\left(\begin{array}{c}1\\1\end{array}\right)}\). Del mismo modo, tenemos
\[ [\color{blue}{u_2}\color{black}{]_{\mathcal{B}}}=\left(\begin{array}{c}-1 \\ \frac{1}{2}\end{array}\right)\quad [\color{Green}{u_3}\color{black}{]_{\mathcal{B}}}=\left(\begin{array}{c}\frac{3}{2} \\ -\frac{1}{2}\end{array}\right)\quad [\color{orange}{u_4}\color{black}{]_{\mathcal{B}}}=\left(\begin{array}{c}0\\ \frac{3}{2}\end{array}\right).\nonumber\]
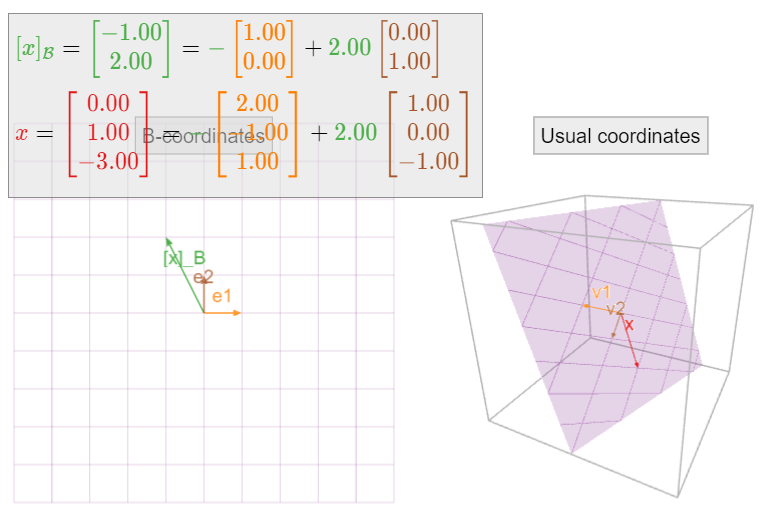
Figura\(\PageIndex{4}\): Izquierda: las\(\mathcal{B}\) coordenadas -de un vector\(x\). Derecha: el vector\(x\). La cuadrícula violeta de la derecha es una imagen del sistema de coordenadas definido por la base\(\mathcal{B}\); un conjunto de líneas mide la\(v_1\) coordenada y el otro conjunto mide la\(v_2\) coordenada. Arrastre las cabezas de los vectores\(x\) y\([x]_{\mathcal{B}}\) para entender la correspondencia entre\(x\) y su vector\(\mathcal{B}\) -coordenada.
Definir
\[v_1=\left(\begin{array}{c}1\\0\\1\end{array}\right),\: v_2=\left(\begin{array}{c}1\\1\\1\end{array}\right),\quad\mathcal{B}=\{v_1,\: v_2\},\quad V=\text{Span}\{v_1,\: v_2\}.\nonumber\]
- Verificar que\(\mathcal{B}\) sea una base para\(V\).
- Si\([w]_{\mathcal{B}}=\left(\begin{array}{c}5\\2\end{array}\right)\), entonces ¿qué es\(w\)?
- Encuentra las\(\mathcal{B}\) coordenadas de\(v=\left(\begin{array}{c}5\\3\\5\end{array}\right)\).
Solución
- Tenemos que verificar que se\(\mathcal{B}\) extiende\(V\), y que es linealmente independiente. Por definición,\(V\) es el lapso de\(\mathcal{B}\); ya que\(v_1\) y no\(v_2\) son múltiplos entre sí, son linealmente independientes. Esto demuestra en particular que\(V\) es un avión.
- Decir\([w]_{\mathcal{B}}=\left(\begin{array}{c}5\\2\end{array}\right)\) significa que\(5\) es la\(v_1\) coordenada de\(w\), y esa\(2\) es la\(v_2\) -coordenada:
\[w=5v_1 +2v_2=5\left(\begin{array}{c}1\\0\\1\end{array}\right)+2\left(\begin{array}{c}1\\1\\1\end{array}\right)=\left(\begin{array}{c}7\\2\\7\end{array}\right).\nonumber\] - Tenemos que resolver la ecuación vectorial\(v=c_1v_1+c_2v_2\) en las incógnitas\(c_1,\: c_2\). Formamos una matriz aumentada y la fila reducimos:
\[\left(\begin{array}{cc|c} 1&1&5\\0&1&3\\1&1&5\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&2\\0&1&3\\0&0&0\end{array}\right).\nonumber\]
Tenemos\(c_1=2\) y\(c_2=3\), así\(v=2v_1+3v_2\) y\([v]_{\mathcal{B}}=\left(\begin{array}{c}2\\3\end{array}\right)\).
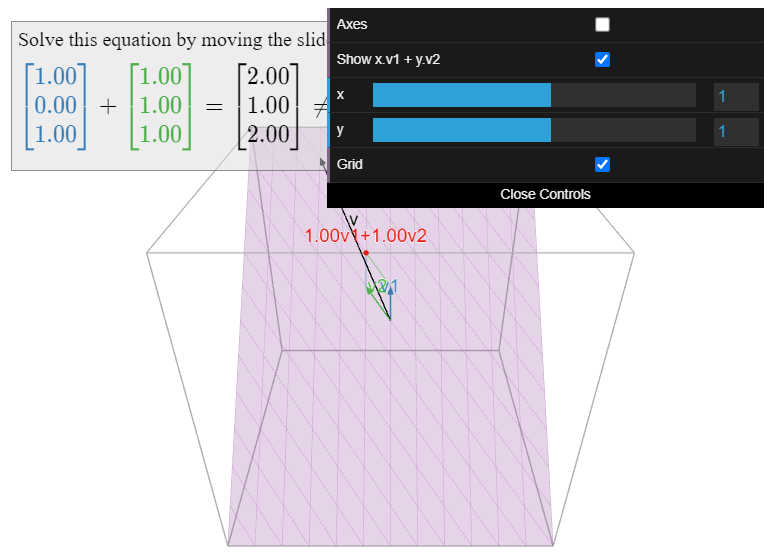
Figura\(\PageIndex{5}\): Una imagen del plano\(V\) y la base\(\mathcal{B}=\{v_1,\: v_2\}\). La cuadrícula violeta es una imagen del sistema de coordenadas definido por la base\(\mathcal{B}\); un conjunto de líneas mide la\(v_1\) coordenada y el otro conjunto mide la\(v_2\) coordenada. Utilice los controles deslizantes para encontrar las\(\mathcal{B}\) coordenadas -de\(v\).
Definir
\[v_1=\left(\begin{array}{c}2\\3\\2\end{array}\right),\quad v_2=\left(\begin{array}{c}-1\\1\\1\end{array}\right),\quad v_3=\left(\begin{array}{c}2\\8\\6\end{array}\right),\quad V=\text{Span}\{v_1,\: v_2,\: v_3\}.\nonumber\]
- Encuentra una base\(\mathcal{B}\) para\(V\).
- Encuentra las\(\mathcal{B}\) coordenadas de\(x=\left(\begin{array}{c}4\\11\\8\end{array}\right).\)
Solución
- Escribimos\(V\) como el espacio de columna de una matriz\(A\), luego row reduce para encontrar las columnas pivotes, como en el Ejemplo 2.7.6, en la Sección 2.7.
\[A=\left(\begin{array}{ccc}2&-1&2\\3&1&8\\2&1&6\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{ccc}1&0&2\\0&1&2\\0&0&0\end{array}\right).\nonumber\]
Las dos primeras columnas son columnas pivotantes, así que podemos tomar\(\mathcal{B}=\{v_1,\:v_2\}\) as our basis for \(V\). - Tenemos que resolver la ecuación vectorial\(x=c_1v_1+c_2v_2\). Formamos una matriz aumentada y la fila
\[\left(\begin{array}{cc|c} 2&-1&4 \\ 3&1&11\\2&1&8\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&3\\0&1&2\\0&0&0\end{array}\right).\nonumber\]
reducimos: Tenemos\(c_1=3\) y\(c_2=2\), así\(x=3v_1+2v_2\), y así\([x]_{\mathcal{B}}=\left(\begin{array}{c}3\\2\end{array}\right)\).
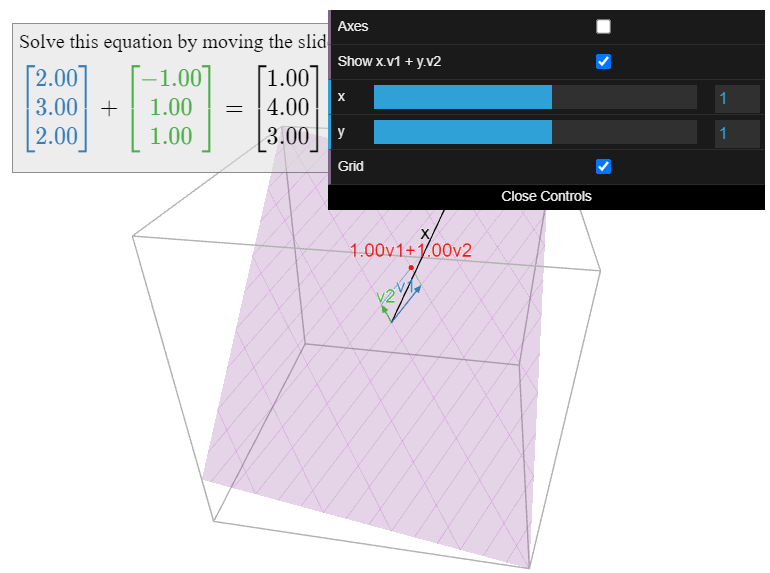
Figura\(\PageIndex{6}\): Una imagen del plano\(V\) y la base\(\mathcal{B}=\{v_1,\:v_2\}\). La cuadrícula violeta es una imagen del sistema de coordenadas definido por la base\(\mathcal{B}\); un conjunto de líneas mide la\(v_1\) coordenada y el otro conjunto mide la\(v_2\) coordenada. Utilice los controles deslizantes para encontrar las\(\mathcal{B}\) coordenadas -de\(x\).
Si\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\) es una base para un subespacio\(V\) y\(x\) está en\(V\), entonces
\[ [x]_{\mathcal{B}}=\left(\begin{array}{c}c_1 \\ c_2 \\ \vdots \\ c_m\end{array}\right)\quad\text{means}\quad x=c_1v_1+c_2v_2+\cdots c_mv_m.\nonumber\]
Encontrar las\(\mathcal{B}\) coordenadas de\(x\) medias resolviendo la ecuación vectorial
\[x=c_1v_1+c_2v_2+\cdots +c_mv_m\nonumber\]
en las incógnitas\(c_1,\: c_2,\cdots ,c_m\). Esto generalmente significa que la fila reduce la matriz aumentada
\[\left(\begin{array}{cccc|c} |&|&\quad&|&| \\ v_1&v_2&\quad &v_m&x \\ |&|&\quad &|&|\end{array}\right).\nonumber\]
\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\)Sea una base de un subespacio\(V\). Encontrar las\(\mathcal{B}\) coordenadas -de un vector\(x\) significa resolver la ecuación vectorial
\[x=c_1v_1+c_2v_2+\cdots +c_mv_m.\nonumber\]
Si no\(x\) está en\(V\), entonces esta ecuación no tiene solución, como no\(x\) está en\(V=\text{Span}\{v_1,\: v_2,\cdots ,v_m\}\). En otras palabras, la ecuación anterior es inconsistente cuando no\(x\) está en\(V\).

