2.9: El teorema del rango
- Page ID
- 113024
- Aprender a entender y utilizar el teorema de rango.
- Imagen: el teorema de rango.
- Teorema: teorema de rango.
- Palabras de vocabulario: rango, nulidad.
En esta sección presentamos el teorema de rangos, que es la culminación de todo el trabajo que hemos realizado hasta ahora.
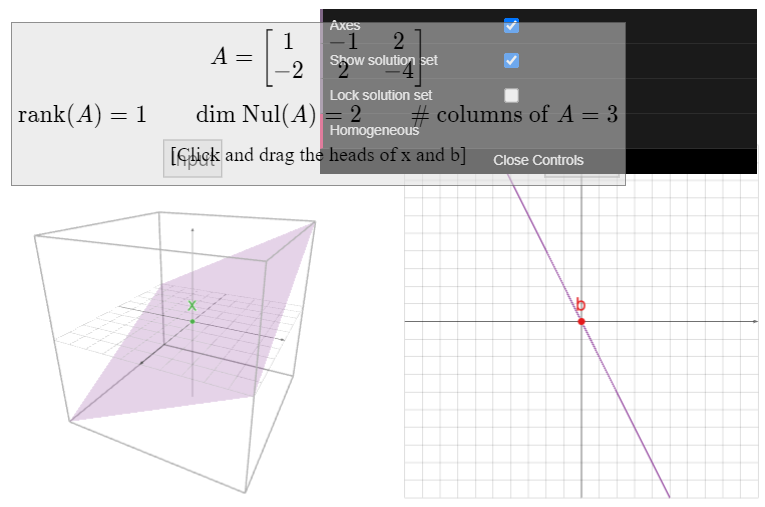
El lector pudo haber observado una relación entre el espacio de columna y el espacio nulo de una matriz. En el Ejemplo 2.6.11 de la Sección 2.6, el espacio de columna y el espacio nulo de una\(3\times 2\) matriz son ambos líneas, en\(\mathbb{R}^2 \) y\(\mathbb{R}^3 \text{,}\) respectivamente:
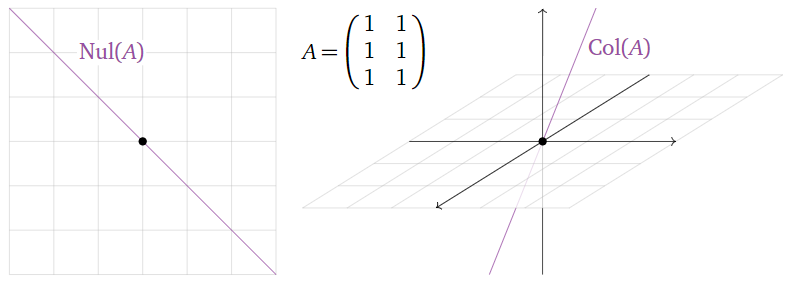
Figura\(\PageIndex{1}\)
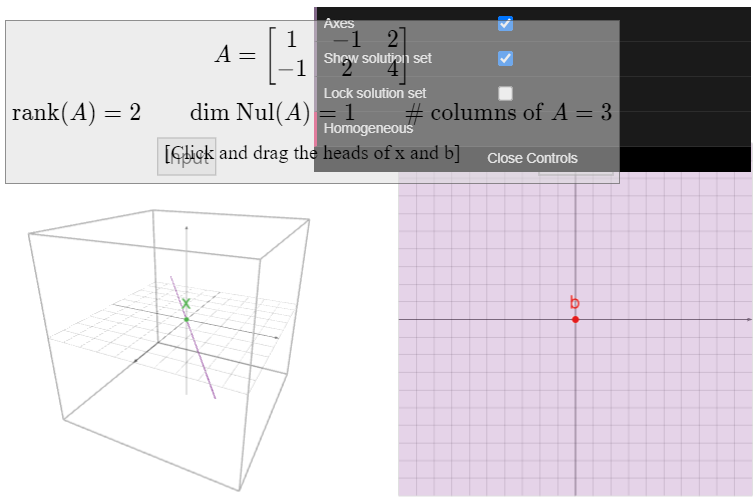
En el Ejemplo 2.4.6 en la Sección 2.4, el espacio nulo de la\(2\times 3\) matriz
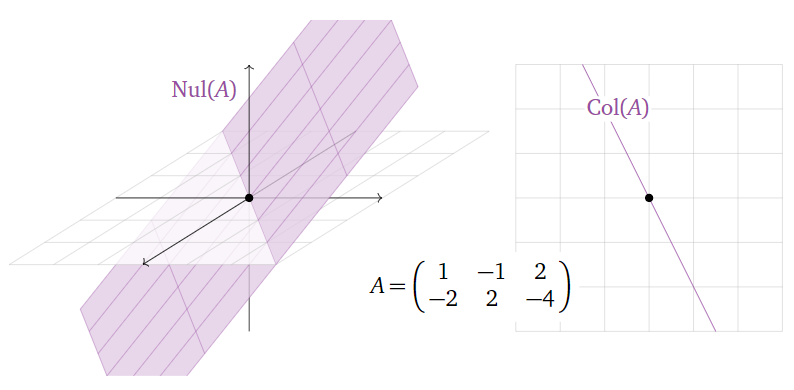
Figura\(\PageIndex{2}\)
En el Ejemplo 2.4.10 de la Sección 2.4, el espacio nulo de una\(3\times 3\) matriz es una línea adentro\(\mathbb{R}^3 \text{,}\) y el espacio de columna es un plano en\(\mathbb{R}^3 \text{:}\)
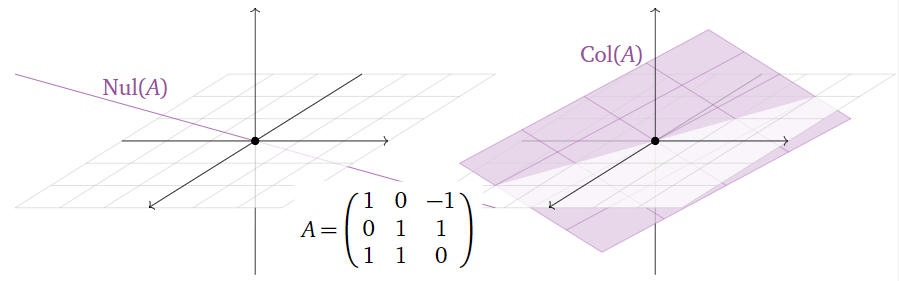
Figura\(\PageIndex{3}\)
En todos los ejemplos, la dimensión del espacio de columna más la dimensión del espacio nulo es igual al número de columnas de la matriz. Este es el contenido del teorema de rango.
El rango de una matriz\(A\text{,}\) escrita\(\text{rank}(A)\text{,}\) es la dimensión del espacio de columna\(\text{Col}(A)\).
La nulidad de una matriz\(A\text{,}\) escrita\(\text{nullity}(A)\text{,}\) es la dimensión del espacio nulo\(\text{Nul}(A)\).
El rango de una matriz nos\(A\) da información importante sobre las soluciones a\(Ax=b\). Recordemos de la Nota 2.3.6 en la Sección 2.3 que\(Ax=b\) es consistente exactamente cuando\(b\) está en el lapso de las columnas de\(A\text{,}\) en otras palabras cuando\(b\) está en el espacio de columna de\(A\). Así,\(\text{rank}(A)\) es la dimensión del conjunto de\(b\) con la propiedad que\(Ax=b\) es consistente.
Sabemos que el rango de\(A\) es igual al número de columnas pivotantes, Definición 1.2.5 en la Sección 1.2, (ver este Teorema 2.7.1 en la Sección 2.7), y la nulidad de\(A\) es igual al número de variables libres (ver este Teorema 2.7.2 en la Sección 2.7), que es el número de columnas sin pivotes. Para resumir:
\[\begin{aligned} \text{rank}(A) = \dim\text{Col}(A) &= \text{the number of columns with pivots}\\ \text{nullity}(A) = \dim\text{Nul}(A) &= \text{the number of free variables}\\ &= \text{the number of columns without pivots} \end{aligned}\]
Claramente
\[ \text{#(columns with pivots)} + \text{#(columns without pivots)} = \text{#(columns)}, \nonumber \]
por lo que hemos demostrado el siguiente teorema.
Si\(A\) es una matriz con\(n\) columnas, entonces
\[ \text{rank}(A) + \text{nullity}(A) = n. \nonumber \]
En otras palabras, para cualquier sistema consistente de ecuaciones lineales,
\[ \text{(dim of column span)} + \text{(dim of solution set)} = \text{(number of variables)}. \nonumber \]
El teorema de rango es realmente la culminación de este capítulo, ya que da una fuerte relación entre el espacio nulo de una matriz (el conjunto de soluciones de\(Ax=0\)) con el espacio de columna (el conjunto de vectores\(b\) haciendo\(Ax=b\) consistente), nuestros dos objetos primarios de interés. Cuanta más libertad tengamos para elegir\(x\) menos libertad tenemos para elegir\(b\) y viceversa.
Aquí hay un ejemplo concreto del teorema de rango y la interacción entre los grados de libertad que tenemos en la elección\(x\) y\(b\) en una ecuación matricial\(Ax=b\).
Considerar las matrices
\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right)\quad\text{and}\quad B=\left(\begin{array}{ccc}0&0&0\\0&0&0\\0&0&1\end{array}\right).\nonumber\]
Si multiplicamos un vector\((x,y,z)\) en\(\mathbb{R}^3 \) por\(A\) y\(B\) obtenemos los vectores\(Ax = (x,y,0)\) y\(Bx = (0,0,z)\). Entonces podemos pensar en la multiplicación dando\(A\) la latitud y longitud de un punto en\(\mathbb{R}^3 \) y podemos pensar en la multiplicación dando\(B\) la altura de un punto en\(\mathbb{R}^3 \). El rango de\(A\) es 2 y la nulidad es 1. De igual manera, el rango de\(B\) es 1 y la nulidad es 2.
Estos hechos tienen interpretaciones naturales. Para la matriz\(A\text{:}\) el conjunto de todas las latitudes y longitudes adentro\(\mathbb{R}^3 \) es un plano, y el conjunto de puntos con la misma latitud y longitud adentro\(\mathbb{R}^3 \) es una línea; y para la matriz\(B\text{:}\) el conjunto de todas las alturas en\(\mathbb{R}^3 \) es una línea, y el conjunto de puntos a una altura dada en\(\mathbb{R}^3 \) es un avión. Como nos dice el teorema de rangos, “intercambiamos” tener más opciones\(x\) por tener más opciones para\(b\text{,}\) y viceversa.
El teorema de rango es un excelente ejemplo de cómo usamos la teoría del álgebra lineal para decir algo cualitativo sobre un sistema de ecuaciones sin resolverlo nunca. Esto es, en esencia, el poder del sujeto.
Considere la siguiente matriz y su forma de escalón de fila reducida:
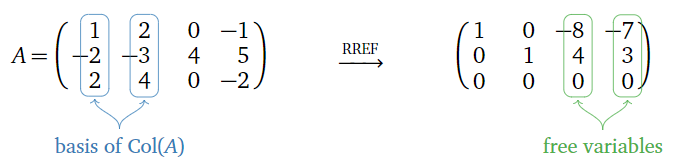
Figura\(\PageIndex{4}\)
Una base para\(\text{Col}(A)\) viene dada por las columnas pivotes:
\[\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\},\nonumber\]
así\(\text{rank}(A) = \dim\text{Col}(A) = 2\).
Como hay dos variables libres\(x_3,x_4\text{,}\) el espacio nulo de\(A\) tiene dos vectores (ver Teorema 2.7.2 en la Sección 2.7):
\[\left\{\left(\begin{array}{c}8\\-4\\1\\0\end{array}\right),\:\left(\begin{array}{c}7\\-3\\0\\1\end{array}\right)\right\},\nonumber\]
así\(\text{nullity}(A) = 2\).
En este caso, el teorema de rango dice que\(2 + 2 = 4\text{,}\) donde 4 es el número de columnas.