5.1: Valores propios y vectores propios
- Page ID
- 113117
- Aprender la definición de vector propio y valor propio.
- Aprende a encontrar vectores propios y valores propios geométricamente.
- Aprender a decidir si un número es un valor propio de una matriz, y si es así, cómo encontrar un vector propio asociado.
- Receta: encontrar una base para el\(\lambda\) -eigenspace.
- Imágenes: si un vector es o no un vector propio, vectores propios de transformaciones de matriz estándar.
- Teorema: el teorema de la matriz invertible expandida.
- Vocabulario palabra: espacio propio.
- Palabras esenciales del vocabulario: vector propio, valor propio.
En esta sección, definimos valores propios y vectores propios. Estos forman la faceta más importante de la teoría de la estructura de las matrices cuadradas. Como tal, los valores propios y los vectores propios tienden a desempeñar un papel clave en las aplicaciones de la vida real del álgebra lineal.
Valores propios y vectores propios
Aquí está la definición más importante en este texto.
\(A\)Déjese ser una\(n\times n\) matriz.
- Un vector propio de\(A\) es un vector distinto de cero\(v\) en\(\mathbb{R}^n \) tal que\(Av=\lambda v\text{,}\) para algunos escalar\(\lambda\).
- Un valor propio de\(A\) es un escalar\(\lambda\) tal que la ecuación\(Av=\lambda v\) tiene una solución no trivial.
Si\(Av = \lambda v\) por\(v\neq 0\text{,}\) decimos que\(\lambda\) es el valor propio para\(v\text{,}\) y que\(v\) es un vector propio para\(\lambda\).
El prefijo alemán “eigen” se traduce aproximadamente como “self” o “own”. Un vector propio de\(A\) es un vector que es llevado a un múltiplo de sí mismo por la transformación matricial\(T(x)=Ax\text{,}\) que quizás explica la terminología. Por otro lado, “eigen” a menudo se traduce como “característico”; podemos pensar en un vector propio como describir una propiedad intrínseca, o característica, de\(A\).
Los valores propios y los vectores propios son solo para matrices cuadradas.
Los vectores propios son, por definición, diferentes de cero. Los valores propios pueden ser iguales a cero.
No consideramos que el vector cero sea un vector propio: ya que\(A0 = 0 = \lambda 0\) para cada escalar\(\lambda\text{,}\) el valor propio asociado sería indefinido.
Si alguien te entrega una matriz\(A\) y un vector\(v\text{,}\) es fácil verificar si\(v\) es un vector propio de\(A\text{:}\) simplemente multiplicar\(v\) por\(A\) y ver si\(Av\) es un múltiplo escalar de\(v\). Por otro lado, dada solo la matriz no es\(A\text{,}\) obvio en absoluto cómo encontrar los vectores propios. Aprenderemos a hacer esto en la Sección 5.2.
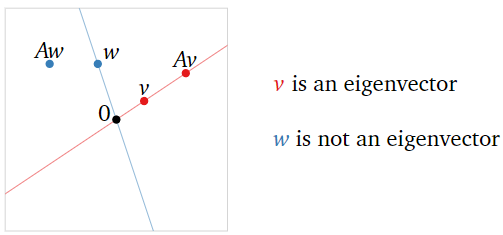
Considerar la matriz
\[ A = \left(\begin{array}{cc}2&2\\-4&8\end{array}\right)\qquad\text{and vectors}\qquad v = \left(\begin{array}{c}1\\1\end{array}\right) \qquad w = \left(\begin{array}{c}2\\1\end{array}\right). \nonumber \]
¿Cuáles son los vectores propios? ¿Cuáles son sus valores propios?
Solución
Tenemos
\[ Av = \left(\begin{array}{cc}2&2\\-4&8\end{array}\right)\left(\begin{array}{c}1\\1\end{array}\right)=\left(\begin{array}{c}4\\4\end{array}\right) = 4v. \nonumber \]
Por lo tanto,\(v\) es un vector propio de\(A\text{,}\) con valor propio\(\lambda = 4\). Por otra parte,
\[ Aw = \left(\begin{array}{cc}2&2\\-4&8\end{array}\right)\left(\begin{array}{c}2\\1\end{array}\right)=\left(\begin{array}{c}6\\0\end{array}\right). \nonumber \]
que no es un múltiplo escalar de\(w\). Por lo tanto, no\(w\) es un vector propio de\(A\).

Figura\(\PageIndex{1}\)
Considerar la matriz
\[ A = \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right)\qquad\text{and vectors}\qquad v = \left(\begin{array}{c}16\\4\\1\end{array}\right) \qquad w = \left(\begin{array}{c}2\\2\\2\end{array}\right). \nonumber \]
¿Cuáles son los vectores propios? ¿Cuáles son sus valores propios?
Solución
Tenemos
\[ Av = \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right) \left(\begin{array}{c}16\\4\\1\end{array}\right) = \left(\begin{array}{c}32\\8\\2\end{array}\right) = 2v. \nonumber \]
Por lo tanto,\(v\) es un vector propio de\(A\text{,}\) con valor propio\(\lambda = 2\). Por otra parte,
\[ Aw = \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right)\left(\begin{array}{c}2\\2\\2\end{array}\right) = \left(\begin{array}{c}28\\1\\1\end{array}\right), \nonumber \]
que no es un múltiplo escalar de\(w\). Por lo tanto, no\(w\) es un vector propio de\(A\).
Let
\[ A = \left(\begin{array}{cc}1&3\\2&6\end{array}\right) \qquad v =\left(\begin{array}{c}-3\\1\end{array}\right). \nonumber \]
Es\(v\) un vector propio de\(A\text{?}\) Si es así, ¿cuál es su valor propio?
Solución
El producto es
\[ Av = \left(\begin{array}{cc}1&3\\2&6\end{array}\right)\left(\begin{array}{c}-3\\1\end{array}\right) = \left(\begin{array}{c}0\\0\end{array}\right) = 0v. \nonumber \]
De ahí\(v\) que sea un vector propio con valor propio cero.
Como se señaló anteriormente, se permite que un valor de eigen sea cero, pero un vector eigen no lo es.
Decir eso\(Av=\lambda v\) significa eso\(Av\) y\(\lambda v\) son colineales con el origen. Entonces, un vector propio de\(A\) es un vector distinto de cero\(v\) tal que\(Av\) y se\(v\) encuentran en la misma línea a través del origen. En este caso,\(Av\) es un múltiplo escalar\(v\text{;}\) del valor propio es el factor de escala.
Figura\(\PageIndex{2}\)
Para las matrices que surgen como la matriz estándar de una transformación lineal, a menudo es mejor dibujar una imagen, luego encontrar los vectores propios y los valores propios geométricamente estudiando qué vectores no se mueven fuera de su línea. Para una transformación que se define geométricamente, no es necesario ni siquiera calcular su matriz para encontrar los vectores propios y los valores propios.
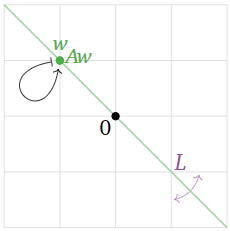
Aquí hay un ejemplo de ello. Dejar\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) ser la transformación lineal que refleja sobre la línea\(L\) definida por\(y=-x\text{,}\) y dejar\(A\) ser la matriz para\(T\). Encontraremos los valores propios y vectores propios de\(A\) sin hacer ningún cálculo.
Esta transformación se define geométricamente, por lo que dibujamos un cuadro.
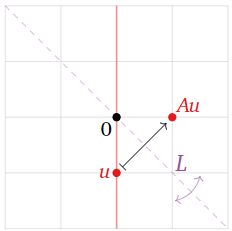
Figura\(\PageIndex{3}\)
El vector no\(\color{Red}{u}\) es un vector propio, porque no\(Au\) es colineal con\(u\) y el origen.
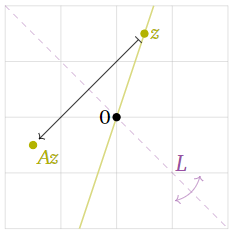
Figura\(\PageIndex{4}\)
El vector tampoco\(\color{YellowGreen}{z}\) es un vector propio.
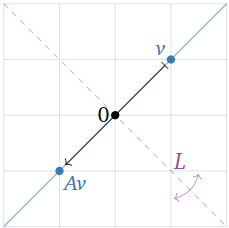
Figura\(\PageIndex{5}\)
El vector\(\color{blue}v\) es un vector propio porque\(Av\) es colineal con\(v\) y el origen. El vector\(Av\) tiene la misma longitud que\(v\text{,}\) pero la dirección opuesta, por lo que el valor propio asociado es\(-1\).
Figura\(\PageIndex{6}\)
El vector\(\color{Green}w\) es un vector propio porque\(Aw\) es colineal con\(w\) y el origen: en efecto,\(Aw\) es igual a\(w\text{!}\) Esto significa que\(w\) es un vector propio con valor propio\(1\).
Parece que todos los vectores propios se encuentran sobre\(L\text{,}\) o en la línea perpendicular a\(L\). Los vectores en\(L\) tienen valor propio\(1\text{,}\) y los vectores perpendiculares para\(L\) tener autovalor\(-1\).
Daremos ahora cinco ejemplos más de esta naturaleza
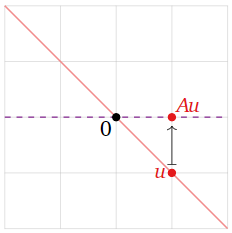
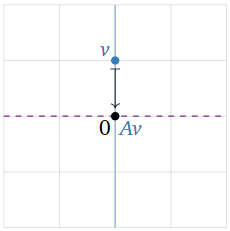
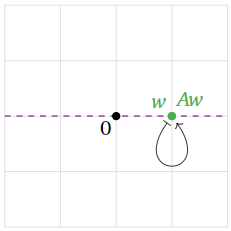
Dejar\(T\colon\mathbb{R}^2\to \mathbb{R}^2\) ser la transformación lineal que proyecta un vector verticalmente sobre el\(x\) -eje, y dejar\(A\) ser la matriz para\(T\). Encuentra los valores propios y vectores propios de\(A\) sin hacer ningún cálculo.
Solución
Esta transformación se define geométricamente, por lo que dibujamos un cuadro.
Figura\(\PageIndex{8}\)
El vector no\(\color{Red}u\) es un vector propio, porque no\(Au\) es colineal con\(u\) y el origen.
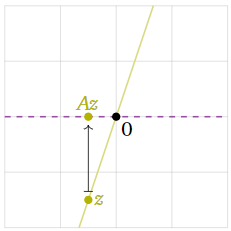
Figura\(\PageIndex{9}\)
El vector tampoco\(\color{YellowGreen}z\) es un vector propio.
Figura\(\PageIndex{10}\)
El vector\(\color{blue}v\) es un vector propio. En efecto,\(Av\) es el vector cero, que es colineal con\(v\) y el origen; ya que\(Av = 0v\text{,}\) el valor propio asociado es\(0\).
Figura\(\PageIndex{11}\)
El vector\(\color{Green}w\) es un vector propio porque\(Aw\) es colineal con\(w\) y el origen: en efecto,\(Aw\) es igual a\(w\text{!}\) Esto significa que\(w\) es un vector propio con valor propio\(1\).
Parece que todos los vectores propios se encuentran en el\(x\) eje -eje o el\(y\) eje -eje. Los vectores en el\(x\) eje -tienen valor propio\(1\text{,}\) y los vectores en el\(y\) eje tienen valor propio\(0\).
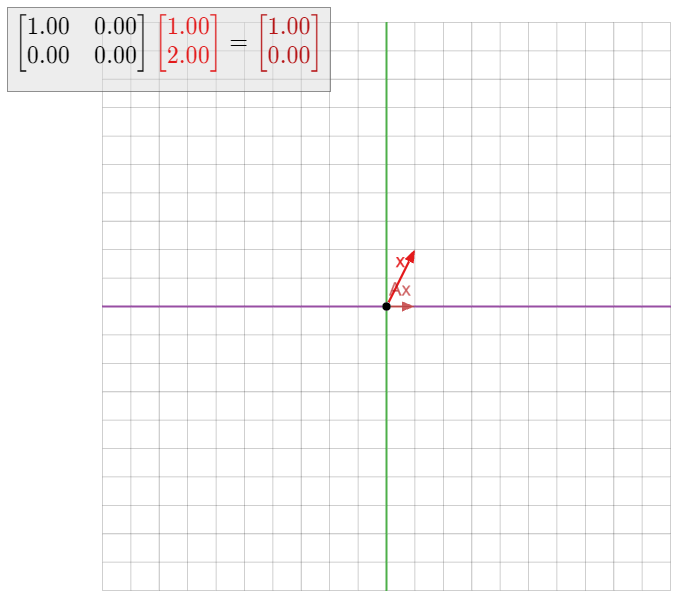
Encuentra todos los valores propios y vectores propios de la matriz de identidad\(I_n\).
Solución
La matriz de identidad tiene la propiedad que\(I_nv = v\) para todos los vectores\(v\) en\(\mathbb{R}^n \). Podemos escribir esto\(I_n v = 1\cdot v\text{,}\) para que cada vector distinto de cero sea un vector propio con valor propio\(1\).
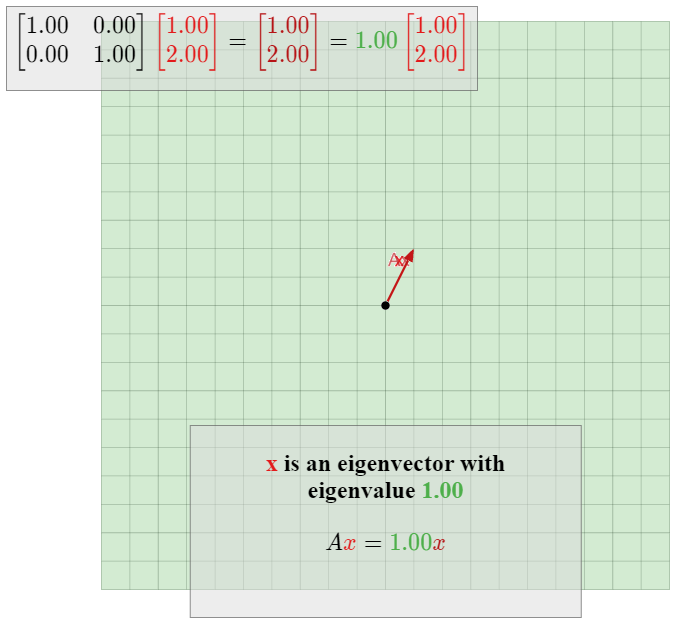
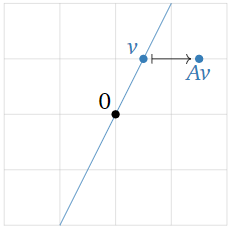
Dejar\(T\colon \mathbb{R} ^2\to \mathbb{R}^2\) ser la transformación lineal que se dilata por un factor de\(1.5\text{,}\) y deja\(A\) ser la matriz para\(T\). Encuentra los valores propios y vectores propios de\(A\) sin hacer ningún cálculo.
Solución
Tenemos
\[ Av = T(v) = 1.5v \nonumber \]
para cada vector\(v\) en\(\mathbb{R}^2\). Por lo tanto, por definición cada vector distinto de cero es un vector propio con valor propio\(1.5.\)
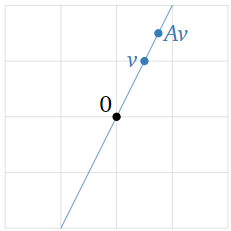
Figura\(\PageIndex{14}\)
Let
\[ A = \left(\begin{array}{cc}1&1\\0&1\end{array}\right) \nonumber \]
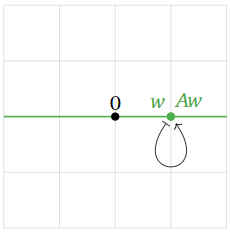
y dejar\(T(x) = Ax\text{,}\) que así\(T\) es una cizalla en la\(x\) dirección -. Encuentra los valores propios y vectores propios de\(A\) sin hacer ningún cálculo.
Solución
En ecuaciones, tenemos
\[ A\left(\begin{array}{c}x\\y\end{array}\right) = \left(\begin{array}{cc}1&1\\0&1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right) = \left(\begin{array}{c}x+y\\y\end{array}\right). \nonumber \]
Esto nos dice que una cizalla toma un vector y agrega su\(y\) coordenada a su\(x\) coordenada. Dado que la\(x\) coordenada -cambia pero no la\(y\) coordenada -, esto nos dice que cualquier vector\(v\) con\(y\) coordenada distinta de cero no puede ser colineal con\(Av\) y el origen.
Figura\(\PageIndex{16}\)
Por otro lado, cualquier vector\(v\) en el\(x\) eje -tiene\(y\) coordenada cero, por lo que no es movido por\(A\). Por lo tanto,\(v\) es un vector propio con valor propio\(1\).
Figura\(\PageIndex{17}\)
En consecuencia, todos los vectores propios de se\(A\) encuentran en el\(x\) eje -y tienen valor propio\(1\).
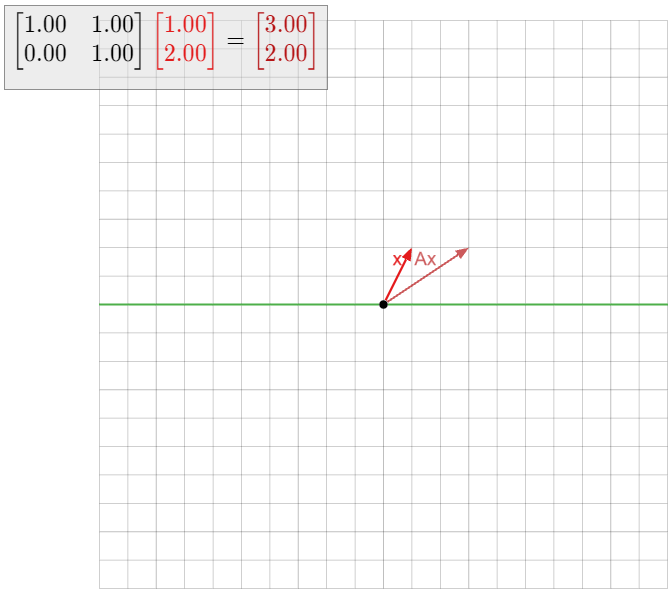
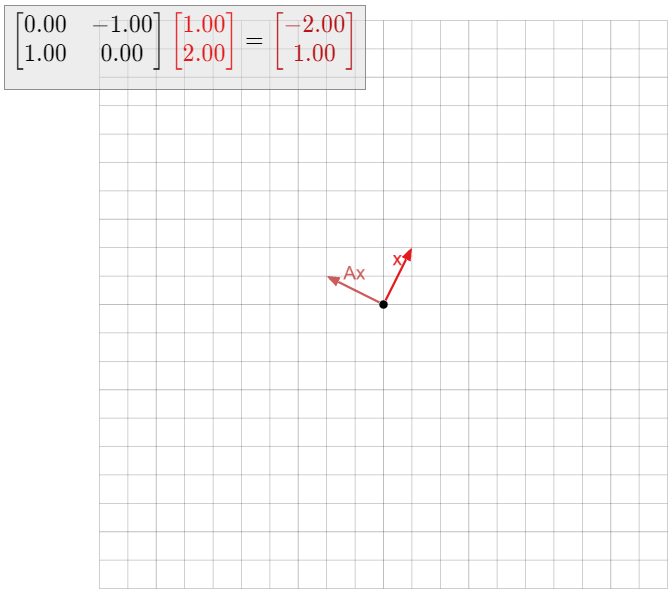
Dejar\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) ser la transformación lineal que gira en sentido antihorario por\(90^\circ\text{,}\) y deja\(A\) ser la matriz para\(T\). Encuentra los valores propios y vectores propios de\(A\) sin hacer ningún cálculo.
Solución
Si\(v\) es cualquier vector distinto de cero, entonces\(Av\) se gira un ángulo de\(90^\circ\) desde\(v\). Por lo tanto, no\(Av\) está en la misma línea ya\(v\text{,}\) que así no\(v\) es un vector propio. Y por supuesto, el vector cero nunca es un vector propio.
Figura\(\PageIndex{19}\)
Por lo tanto, esta matriz no tiene vectores propios y valores propios.
Aquí mencionamos un dato básico sobre los vectores propios.
Dejar\(v_1,v_2,\ldots,v_k\) ser vectores propios de una matriz\(A\text{,}\) y supongamos que los valores propios correspondientes\(\lambda_1,\lambda_2,\ldots,\lambda_k\) son distintos (todos diferentes entre sí). Entonces\(\{v_1,v_2,\ldots,v_k\}\) es linealmente independiente.
- Prueba
-
Supongamos que\(\{v_1,v_2,\ldots,v_k\}\) fueran linealmente de pendent. De acuerdo con el criterio de lapso creciente, Teorema 2.5.2 en la Sección 2.5, esto significa que para algunos\(j\text{,}\) el vector\(v_j\) está en\(\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}.\) Si elegimos el primero tal\(j\text{,}\) entonces\(\{v_1,v_2,\ldots,v_{j-1}\}\) es linealmente independiente. Tenga en cuenta que\(j > 1\) desde\(v_1\neq 0\).
Ya que\(v_j\) está en\(\text{Span}\{v_1,v_2,\ldots,v_{j-1}\},\text{,}\) podemos escribir
\[ v_j = c_1v_1 + c_2v_2 + \cdots + c_{j-1}v_{j-1} \nonumber \]
para algunos escalares\(c_1,c_2,\ldots,c_{j-1}\). Multiplicar ambos lados de la ecuación anterior por\(A\) da
\[ \begin{split} \lambda_jv_j = Av_j \amp= A\bigl(c_1v_1 + c_2v_2 + \cdots + c_{j-1}v_{j-1}\bigr) \\ \amp= c_1Av_1 + c_2Av_2 + \cdots + c_{j-1}Av_{j-1} \\ \amp= c_1\lambda_1v_1 + c_2\lambda_2v_2 + \cdots + c_{j-1}\lambda_{j-1}v_{j-1}. \end{split} \nonumber \]
Restar\(\lambda_j\) veces la primera ecuación de la segunda da
\[ 0 = \lambda_jv_j - \lambda_jv_j = c_1(\lambda_1-\lambda_j)v_1 + c_2(\lambda_2-\lambda_j)v_2 + \cdots + c_{j-1}(\lambda_{j-1}-\lambda_j)v_{j-1}. \nonumber \]
Ya que\(\lambda_i\neq\lambda_j\) para\(i \lt j\text{,}\) ello hay una ecuación de dependencia lineal entre la\(v_1,v_2,\ldots,v_{j-1}\text{,}\) que es imposible porque esos vectores son linealmente independientes. Por lo tanto,\(\{v_1,v_2,\ldots,v_k\}\) debe haber sido linealmente independiente después de todo.
Cuando\(k=2\text{,}\) esto dice que si\(v_1,v_2\) son vectores propios con valores propios\(\lambda_1\neq\lambda_2\text{,}\) entonces no\(v_2\) es un múltiplo de\(v_1\). De hecho, cualquier múltiplo distinto\(cv_1\) de cero de también\(v_1\) es un vector propio con valor propio\(\lambda_1\text{:}\)
\[ A(cv_1) = cAv_1 = c(\lambda_1 v_1) = \lambda_1(cv_1). \nonumber \]
Como consecuencia del hecho anterior\(\PageIndex{1}\), tenemos lo siguiente.
Una\(n\times n\) matriz\(A\) tiene como máximo\(n\) valores propios.
Eigenspaces
Supongamos que\(A\) es una matriz cuadrada. Ya sabemos cómo verificar si un vector dado es un vector propio de\(A\) y en ese caso encontrar el valor propio. Nuestro siguiente objetivo es verificar si un número real dado es un valor propio de\(A\) y en ese caso encontrar todos los vectores propios correspondientes. Nuevamente esto será sencillo, pero más involucrado. La única pieza que falta, entonces, será encontrar los valores propios de\(A\text{;}\) ésta es el contenido principal de la Sección 5.2.
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\(\lambda\) ser un escalar. Los vectores propios con valor propio\(\lambda\text{,}\) si los hay, son las soluciones distintas de cero de la ecuación\(Av=\lambda v\). Podemos reescribir esta ecuación de la siguiente manera:
\[ \begin{split} \amp Av = \lambda v \\ \iff\quad \amp Av - \lambda v = 0 \\ \iff\quad \amp Av - \lambda I_nv = 0 \\ \iff\quad \amp(A - \lambda I_n)v = 0. \end{split} \nonumber \]
Por lo tanto, los vectores propios de\(A\) con valor propio\(\lambda\text{,}\) si los hay, son las soluciones no triviales de la ecuación matricial\((A-\lambda I_n)v = 0\text{,}\) es decir, los vectores distintos de cero en\(\text{Nul}(A-\lambda I_n)\). Si esta ecuación no tiene soluciones no triviales, entonces no\(\lambda\) es un vector propio de\(A\).
La observación anterior es importante porque dice que encontrar los vectores propios para un valor propio dado significa resolver un sistema homogéneo de ecuaciones. Por ejemplo, si
\[ A = \left(\begin{array}{ccc}7&1&3\\-3&2&-3\\-3&-2&-1\end{array}\right), \nonumber \]
entonces un vector propio con valor propio\(\lambda\) es una solución no trivial de la ecuación matricial
\[ \left(\begin{array}{ccc}7&1&3\\-3&2&-3\\-3&-2&-1\end{array}\right)\left(\begin{array}{c}x\\y\\z\end{array}\right) = \lambda \left(\begin{array}{c}x\\y\\z\end{array}\right). \nonumber \]
Esto se traduce en el sistema de ecuaciones
\[\left\{\begin{array}{rrrrrrr} 7x &+& y &+& 3z &=& \lambda x \\ -3x &+& 2y &-& 3z &=& \lambda y \\ -3x& -& 2y& -& z& =& \lambda z\end{array}\right.\quad\longrightarrow\quad\left\{\begin{array}{rrrrrrl} (7-\lambda)x &+& y &+& 3z &=& 0 \\ -3x &+& (2-\lambda)y &-& 3z &=& 0 \\ -3x& -& 2y &+& (-1-\lambda)z &=& 0.\end{array}\right.\nonumber\]
Esto es lo mismo que la ecuación de matriz homogénea
\[ \left(\begin{array}{ccc}7-\lambda &1&3\\-3&2-\lambda&-3 \\ -3&-2&-1-\lambda\end{array}\right)\left(\begin{array}{c}x\\y\\z\end{array}\right) = 0, \nonumber \]
es decir,\((A-\lambda I_3)v = 0\).
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\(\lambda\) ser un valor propio de\(A\). El \(\lambda\)-espacio propio de\(A\) es el conjunto de soluciones de\((A-\lambda I_n)v=0\text{,}\) i.e., el subespacio\(\text{Nul}(A-\lambda I_n)\).
El\(\lambda\) -espacio propio es un subespacio porque es el espacio nulo de una matriz, es decir, la matriz\(A-\lambda I_n\). Este subespacio consiste en el vector cero y todos los vectores propios de\(A\) con autovalor\(\lambda\).
Dado que un subespacio distinto de cero es infinito, cada valor propio tiene infinitamente muchos vectores propios. (Por ejemplo, multiplicar un vector propio por un escalar distinto de cero da otro vector propio). Por otro lado, puede haber como máximo vectores propios\(n\) linealmente independientes de una\(n\times n\) matriz, ya que\(\mathbb{R}^n \) tiene dimensión\(n\).
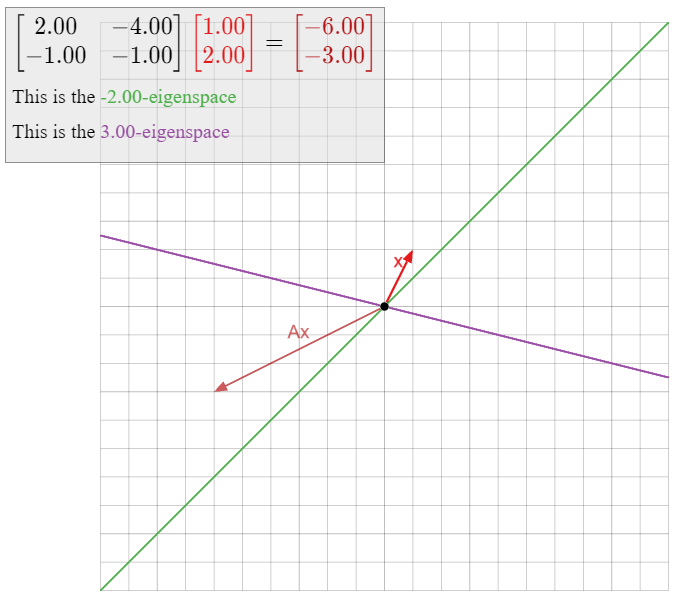
Para cada uno de los números\(\lambda = -2, 1, 3\text{,}\) decidir si\(\lambda\) es un valor propio de la matriz
\[ A = \left(\begin{array}{cc}2&-4\\-1&-1\end{array}\right), \nonumber \]
y si es así, computar una base para el\(\lambda\) -eigenspace.
Solución
El número\(3\) es un valor propio de\(A\) si y solo si\(\text{Nul}(A-3I_2)\) es distinto de cero. De ahí que tengamos que resolver la ecuación matricial\((A-3I_2)v = 0\). Tenemos
\[ A - 3I_2 =\left(\begin{array}{cc}2&-4\\-1&-1\end{array}\right) - 3\left(\begin{array}{cc}1&0\\0&1\end{array}\right) = \left(\begin{array}{cc}-1&-4\\-1&-4\end{array}\right). \nonumber \]
La forma de escalón de fila reducida de esta matriz es
\[\left(\begin{array}{cc}1&4\\0&0\end{array}\right)\quad\xrightarrow{\begin{array}{c}\text{parametric}\\ \text{form}\end{array}}\quad\left\{\begin{array}{rrr}x&=&-4y\\y&=&y\end{array}\right.\quad\xrightarrow{\begin{array}{c}\text{parametric}\\ \text{vector form}\end{array}}\quad\left(\begin{array}{c}x\\y\end{array}\right)=y\left(\begin{array}{c}-4\\1\end{array}\right).\nonumber\]
Dado que\(y\) es una variable libre, el espacio nulo de\(A-3I_2\) es distinto de cero, por lo que\(3\) es un vector propio. Una base para el\(3\) -eigenspace es\(\bigl\{{-4\choose 1}\bigr\}.\)
Concretamente, hemos demostrado que los vectores propios de\(A\) con valor propio\(3\) son exactamente los múltiplos distintos de cero de\({-4\choose 1}\). En particular,\(-4\choose 1\) es un vector propio, que podemos verificar:
\[\left(\begin{array}{cc}2&-4\\-1&1\end{array}\right)\left(\begin{array}{c}-4\\1\end{array}\right)=\left(\begin{array}{c}-12\\3\end{array}\right)=3\left(\begin{array}{c}-4\\1\end{array}\right).\nonumber\]
El número\(1\) es un valor propio de\(A\) si y solo si\(\text{Nul}(A-I_2)\) es distinto de cero. De ahí que tengamos que resolver la ecuación matricial\((A-I_2)v = 0\). Tenemos
\[A-I_{2}=\left(\begin{array}{cc}2&-4\\-1&-1\end{array}\right)-\left(\begin{array}{cc}1&0\\0&1\end{array}\right)=\left(\begin{array}{cc}1&-4\\-1&-2\end{array}\right).\nonumber\]
Esta matriz tiene determinante\(-6\text{,}\) por lo que es invertible. Por Teorema 3.6.1 en la Sección 3.6, tenemos\(\text{Nul}(A-I_2) = \{0\}\text{,}\) así que no\(1\) es un valor propio.
Los vectores propios de\(A\) con valor propio\(-2\text{,}\) si los hay, son las soluciones distintas de cero de la ecuación matricial\((A+2I_2)v = 0\). Tenemos
\[A+2I_{2}=\left(\begin{array}{cc}2&-4\\-1&-1\end{array}\right)+2\left(\begin{array}{cc}1&0\\0&1\end{array}\right)=\left(\begin{array}{cc}4&-4\\-1&1\end{array}\right).\nonumber\]
La forma de escalón de fila reducida de esta matriz es
\[\left(\begin{array}{cc}1&-1\\0&0\end{array}\right)\quad\xrightarrow{\begin{array}{c}\text{parametric}\\ \text{form}\end{array}}\quad\left\{\begin{array}{rrr}x&=&y\\y&=&y\end{array}\right.\quad\xrightarrow{\begin{array}{c}\text{parametric}\\ \text{vector form}\end{array}}\quad\left(\begin{array}{c}x\\y\end{array}\right)=y\left(\begin{array}{c}1\\1\end{array}\right).\nonumber\]
Por lo tanto, existen vectores propios con valor propio,\(-2\text{,}\) es decir, cualquier múltiplo distinto de cero de la base\({1\choose 1}.\) A para el\(-2\) espacio propio es\(\bigl\{{1\choose 1}\bigr\}.\)
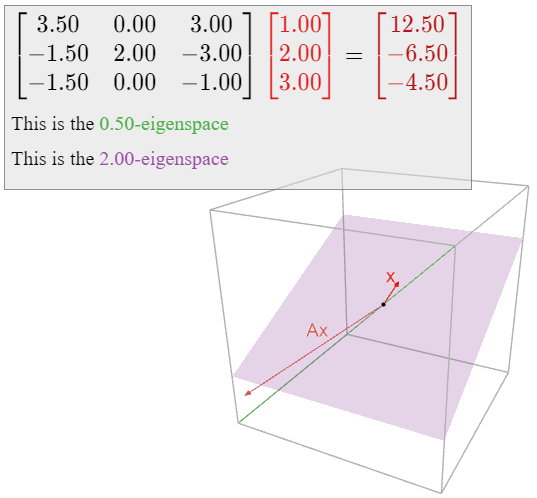
Para cada uno de los números\(\lambda=0, \frac 12, 2\text{,}\) decidir si\(\lambda\) es un vector propio de la matriz
\[A=\left(\begin{array}{ccc}7/2&0&3\\ -3/2&2&-3\\ -3/2&0&-1\end{array}\right),\nonumber\]
y si es así, computar una base para el\(\lambda\) -eigenspace.
Solución
El número\(2\) es un valor propio de\(A\) si y solo si\(\text{Nul}(A-2I_3)\) es distinto de cero. De ahí que tengamos que resolver la ecuación matricial\((A-2I_3)v = 0\). Tenemos
\[A-2I_{3}=\left(\begin{array}{ccc}7/2&0&3 \\ -3/2&2&-3\\ -3/2&0&1\end{array}\right) -2\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)=\left(\begin{array}{ccc}3/2&0&3 \\ -3/2&0&-3\\ -3/2&0&-3\end{array}\right).\nonumber\]
La forma de escalón de fila reducida de esta matriz es
\[\left(\begin{array}{ccc}1&0&2\\0&0&0\\0&0&0\end{array}\right)\quad\xrightarrow{\begin{array}{c}\text{parametric} \\ \text{form}\end{array}}\quad\left\{\begin{array}{rrr}x&=&-2z \\ y&=&y \\ z&=&z\end{array}\right.\quad\xrightarrow{\begin{array}{c}\text{parametric}\\ \text{vector form}\end{array}}\quad\left(\begin{array}{c}x\\y\\z\end{array}\right)=y\left(\begin{array}{c}0\\1\\0\end{array}\right)+z\left(\begin{array}{c}-2\\0\\1\end{array}\right).\nonumber\]
La matriz\(A-2I_3\) tiene dos variables libres, por lo que el espacio nulo de\(A-2I_3\) es distinto de cero, y por lo tanto\(2\) es un vector propio. Una base para el\(2\) -eigenspace es
\[ \left\{\left(\begin{array}{c}0\\1\\0\end{array}\right),\,\left(\begin{array}{c}-2\\0\\1\end{array}\right)\right\}. \nonumber \]
Este es un avión en\(\mathbb{R}^3 \).
Los vectores propios de\(A\) con valor propio\(\frac 12\text{,}\) si los hay, son las soluciones distintas de cero de la ecuación matricial\((A-\frac 12I_3)v = 0\). Tenemos
\[A-\frac{1}{2}I_{3}=\left(\begin{array}{ccc}7/2&0&3\\ -3/2&2&-3\\ -3/2&0&1\end{array}\right)-\frac{1}{2}\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)=\left(\begin{array}{ccc}3&0&3\\-3/2&3/2&-3 \\ -3/2&0&-3/2\end{array}\right).\nonumber\]
La forma de escalón de fila reducida de esta matriz es
\[\left(\begin{array}{ccc}1&0&1\\0&1&-1\\0&0&0\end{array}\right)\quad\xrightarrow{\begin{array}{c}\text{parametric}\\ \text{form}\end{array}}\quad\left\{\begin{array}{rrr}x&=&-z\\ y&=&z \\ z&=&z\end{array}\right.\quad\xrightarrow{\begin{array}{c}\text{parametric} \\ \text{vector form}\end{array}}\quad\left(\begin{array}{c}x\\y\\z\end{array}\right)=z\left(\begin{array}{c}-1\\1\\1\end{array}\right).\nonumber\]
De ahí que existan vectores propios con valor propio,\(\frac 12\text{,}\) por lo que\(\frac 12\) es un valor propio. Una base para el\(\frac 12\) -eigenspace es
\[ \left\{\left(\begin{array}{c}-1\\1\\1\end{array}\right)\right\}. \nonumber \]
Esta es una línea en\(\mathbb{R}^3 \).
El número\(0\) es un valor propio de\(A\) si y solo si\(\text{Nul}(A-0I_3) = \text{Nul}(A)\) es distinto de cero. Esto es lo mismo que preguntar si\(A\) es ininvertible, por el Teorema 3.6.1 en la Sección 3.6. El determinante de\(A\) es\(\det(A) = 2\neq 0\text{,}\) así\(A\) es invertible por la propiedad de invertibilidad, Proposición 4.1.2 en la Sección 4.1. De ello\(0\) se deduce que no es un valor propio de\(A\).
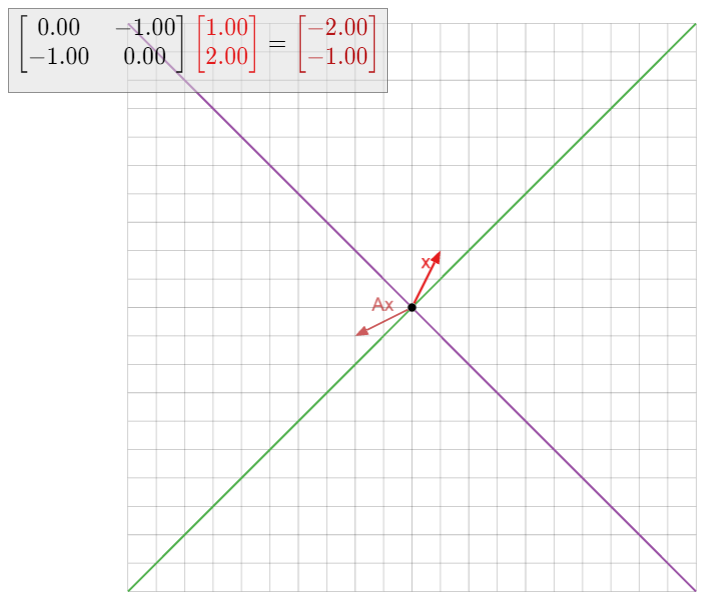
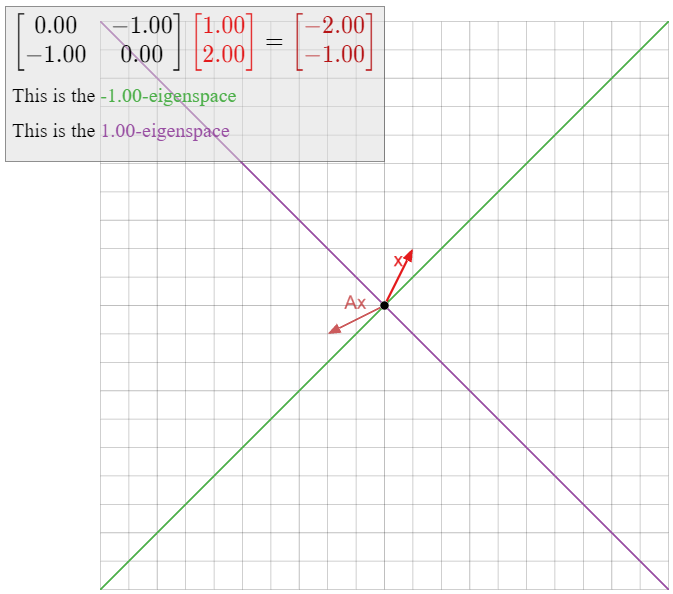
Dejar\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) ser la transformación lineal que refleja sobre la línea\(L\) definida por\(y=-x\text{,}\) y dejar\(A\) ser la matriz para\(T\). Encuentra todos los espacios propios de\(A\).
Solución
Mostramos en Ejemplo\(\PageIndex{4}\) que todos los vectores propios con valor propio se\(1\) encuentran sobre\(L\text{,}\) y todos los vectores propios con autovalor se\(-1\) encuentran en la línea\(L^\perp\) que es perpendicular a\(L\). De ahí,\(L\) es el\(1\) -espacio propio, y\(L^\perp\) es el\(-1\) -espacio propio.
Nada de esto requirió cálculos, pero podemos verificar nuestras conclusiones usando álgebra. Primero calculamos la matriz\(A\text{:}\)
\[T\left(\begin{array}{c}1\\0\end{array}\right)=\left(\begin{array}{c}0\\-1\end{array}\right)\quad T\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}-1\\0\end{array}\right)\quad\implies\quad A=\left(\begin{array}{cc}0&-1\\-1&0\end{array}\right).\nonumber\]
Calcular el\(1\) espacio propio significa resolver la ecuación matricial\((A-I_2)v=0\). Tenemos
\[A-I_{2}=\left(\begin{array}{cc}0&-1\\-1&0\end{array}\right)-\left(\begin{array}{cc}1&0\\0&1\end{array}\right)=\left(\begin{array}{cc}-1&-1\\-1&-1\end{array}\right)\quad\xrightarrow{\text{RREF}}\quad\left(\begin{array}{cc}1&1\\0&0\end{array}\right).\nonumber\]
La forma paramétrica del conjunto de soluciones es\(x = -y\text{,}\) o equivalentemente,\(y = -x\text{,}\) que es exactamente la ecuación para\(L\). Calcular el\(-1\) espacio propio significa resolver la ecuación matricial\((A+I_2)v=0\text{;}\) que tenemos
\[A+I_{2}=\left(\begin{array}{cc}0&-1\\-1&0\end{array}\right)+\left(\begin{array}{cc}1&0\\0&1\end{array}\right)=\left(\begin{array}{cc}1&-1\\-1&1\end{array}\right)\quad\xrightarrow{\text{RREF}}\quad\left(\begin{array}{cc}1&-1\\0&0\end{array}\right).\nonumber\]
La forma paramétrica del conjunto de soluciones es\(x = y\text{,}\) o equivalentemente,\(y = x\text{,}\) que es exactamente la ecuación para\(L^\perp\).
Dejar\(A\) ser una\(n\times n\) matriz y dejar\(\lambda\) ser un número.
- \(\lambda\)es un valor propio de\(A\) si y solo si\((A-\lambda I_n)v = 0\) tiene una solución no trivial, si y solo si\(\text{Nul}(A-\lambda I_n)\neq\{0\}.\)
- En este caso, encontrar una base para el\(\lambda\) -propio espacio de\(A\) medias encontrando una base para la\(\text{Nul}(A-\lambda I_n)\text{,}\) cual se puede hacer encontrando la forma vectorial paramétrica de las soluciones del sistema homogéneo de ecuaciones\((A-\lambda I_n)v = 0\).
- La dimensión del\(\lambda\) espacio propio de\(A\) es igual al número de variables libres en el sistema de ecuaciones\((A-\lambda I_n)v = 0\text{,}\) que es el número de columnas de\(A - \lambda I_n\) sin pivotes.
- Los vectores propios con valor propio\(\lambda\) son los vectores distintos de cero en\(\text{Nul}(A-\lambda I_n),\) o equivalentemente, las soluciones no triviales de\((A-\lambda I_n)v = 0\).
Concluimos con una observación sobre el\(0\) espacio propio de una matriz.
\(A\)Déjese ser una\(n\times n\) matriz.
- El número\(0\) es un valor propio de\(A\) si y sólo si no\(A\) es invertible.
- En este caso, el\(0\) -propio espacio de\(A\) es\(\text{Nul}(A)\).
- Prueba
-
Sabemos que\(0\) es un valor propio de\(A\) si y solo si\(\text{Nul}(A - 0I_n) = \text{Nul}(A)\) es distinto de cero, lo que equivale a la no invertibilidad de\(A\) por Teorema 3.6.1 en la Sección 3.6. En este caso, el\(0\) -eigenspace es por definición\(\text{Nul}(A-0I_n) = \text{Nul}(A)\).
Concretamente, un vector propio con valor propio\(0\) es un vector distinto de cero\(v\) tal que\(Av=0v\text{,}\) es decir, tal que\(Av = 0\). Estos son exactamente los vectores distintos de cero en el espacio nulo de\(A\).
El teorema de la matriz invertible: Addenda
Ahora tenemos dos nuevas formas de decir que una matriz es invertible, por lo que las agregamos al teorema de la matriz invertible, Teorema 3.6.1 en la Sección 3.6.
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^n \) ser la transformación matricial\(T(x) = Ax\). Las siguientes declaraciones son equivalentes:
- \(A\)es invertible.
- \(A\)tiene\(n\) pivotes.
- \(\text{Nul}(A) = \{0\}\).
- Las columnas de\(A\) son linealmente independientes.
- Las columnas de\(A\) span\(\mathbb{R}^n \).
- \(Ax=b\)tiene una solución única para cada uno\(b\) en\(\mathbb{R}^n \).
- \(T\)es invertible.
- \(T\)es uno a uno.
- \(T\)está en.
- \(\det(A) \neq 0\).
- \(0\)no es un valor propio de\(A\).


