5.2: El polinomio característico
- Page ID
- 113129
- Aprende que los valores propios de una matriz triangular son las entradas diagonales.
- Encuentra todos los valores propios de una matriz usando el polinomio característico.
- Aprender algunas estrategias para encontrar los ceros de un polinomio.
- Receta: el polinomio característico de una\(2\times 2\) matriz.
- Palabras de vocabulario: polinomio característico, traza.
En la Sección 5.1 discutimos cómo decidir si un número dado\(\lambda\) es un valor propio de una matriz, y si es así, cómo encontrar todos los vectores propios asociados. En esta sección, daremos un método para computar todos los valores propios de una matriz. Esto no reduce a resolver un sistema de ecuaciones lineales: de hecho, requiere resolver una ecuación no lineal en una variable, es decir, encontrar las raíces del polinomio característico.
\(A\)Déjese ser una\(n\times n\) matriz. El polinomio característico de\(A\) es la función\(f(\lambda)\) dada por
\[ f(\lambda) = \det(A-\lambda I_n). \nonumber \]
A continuación veremos, Teorema\(\PageIndex{2}\), que el polinomio característico es de hecho un polinomio. Encontrar el polinomio característico significa computar el determinante de la matriz\(A-\lambda I_n\text{,}\) cuyas entradas contienen lo desconocido\(\lambda\).
Encuentra el polinomio característico de la matriz
\[ A = \left(\begin{array}{cc}5&2\\2&1\end{array}\right). \nonumber \]
Solución
Tenemos
\[\begin{aligned}f(\lambda)=\det(A-\lambda I_{2})&=\det\left(\left(\begin{array}{cc}5&2\\2&1\end{array}\right)-\left(\begin{array}{cc}\lambda&0\\0&\lambda\end{array}\right)\right) \\ &=\det\left(\begin{array}{cc}5-\lambda&2\\2&1-\lambda\end{array}\right) \\ &=(5-\lambda)(1-\lambda)-2\cdot 2=\lambda^{2}-6\lambda+1.\end{aligned}\]
Encuentra el polinomio característico de la matriz
\[ A = \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right). \nonumber \]
Solución
Calculamos el determinante expandiendo cofactores a lo largo de la tercera columna:
\[\begin{aligned}f(\lambda)=\det(A-\lambda I_{3})&=\det\left(\begin{array}{ccc}-\lambda&6&8\\ \frac{1}{2}&-\lambda&0 \\ 0&\frac{1}{2}&-\lambda\end{array}\right) \\ &=8\left(\frac{1}{4}-0\cdot -\lambda\right)-\lambda\left(\lambda^{2}-6\cdot\frac{1}{2}\right) \\ &=-\lambda^{3}+3\lambda+2.\end{aligned}\]
El punto del polinomio característico es que podemos usarlo para calcular valores propios.
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\(f(\lambda) = \det(A-\lambda I_n)\) ser su polinomio característico. Entonces un número\(\lambda_0\) es un valor propio de\(A\) si y solo si\(f(\lambda_0) = 0\).
- Prueba
-
Por el Teorema 5.1.1 en la Sección 5.1, la ecuación matricial\((A-\lambda_0 I_n)x=0\) tiene una solución no trivial si y solo si\(\det(A-\lambda_0 I_n) = 0\). Por lo tanto,
\[ \begin{split} \lambda_0 \text{ is an eigenvalue of } A \amp\iff Ax = \lambda_0 x \text{ has a nontrivial solution} \\ \amp\iff (A-\lambda_0 I_n)x = 0 \text{ has a nontrivial solution} \\ \amp\iff A - \lambda_0 I_n \text{ is not invertible} \\ \amp\iff \det(A - \lambda_0 I_n) = 0 \\ \amp\iff f(\lambda_0) = 0. \end{split} \nonumber \]
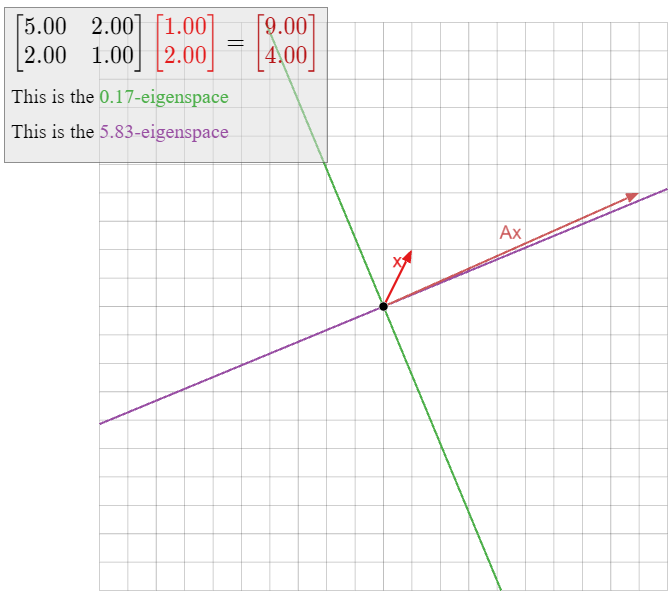
Encuentra los valores propios y los vectores propios de la matriz
\[ A = \left(\begin{array}{cc}5&2\\2&1\end{array}\right). \nonumber \]
Solución
En el Ejemplo anterior\(\PageIndex{1}\) calculamos el polinomio característico de\(A\) ser\(f(\lambda) = \lambda^2-6\lambda + 1\). Podemos resolver la ecuación\(\lambda^2-6\lambda+1=0\) usando la fórmula cuadrática:
\[ \lambda = \frac{6\pm\sqrt{36-4}}2 = 3\pm 2\sqrt 2. \nonumber \]
Por lo tanto, los valores propios son\(3+2\sqrt 2\) y\(3-2\sqrt 2\).
Para calcular los vectores propios, resolvemos el sistema homogéneo de ecuaciones\((A-\lambda I_2)x=0\) para cada autovalor\(\lambda\). Cuando\(\lambda=3+2\sqrt 2\text{,}\) tenemos
\[ \begin{split} A-(3+\sqrt 2)I_2 = \amp\left(\begin{array}{cc}2-2\sqrt{2}&2\\2&-2-2\sqrt{2}\end{array}\right) \\ \xrightarrow{R_1 = R_1\times(2+2\sqrt2)}\; \amp\left(\begin{array}{cc}-4&4+4\sqrt{2}\\2&-2-2\sqrt{2}\end{array}\right) \\ \xrightarrow{R_2 = R_2+R_1/2}\; \amp\left(\begin{array}{cc}-4&4+4\sqrt{2}\\0&0\end{array}\right) \\ \xrightarrow{R_1 = R_1 \div -4}\; \amp\left(\begin{array}{cc}1&-1-\sqrt{2}\\0&0\end{array}\right). \end{split} \nonumber \]
La forma paramétrica de la solución general es\(x=(1+\sqrt 2)y\text{,}\) así que el\((3+2\sqrt 2)\) -espacio propio es la línea abarcada por\({1+\sqrt 2\choose 1}\). Calculamos de la misma manera que el\((3-2\sqrt 2)\) -eigenspace es la línea abarcada por\({1-\sqrt 2\choose 1}\).
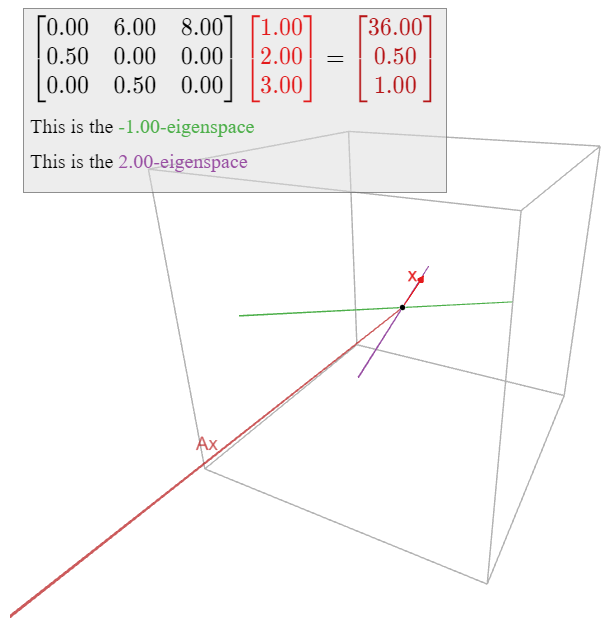
Encuentra los valores propios y los vectores propios de la matriz
\[ A = \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right). \nonumber \]
Solución
En el Ejemplo anterior\(\PageIndex{2}\) calculamos el polinomio característico de\(A\) ser\(f(\lambda) = -\lambda^3+3\lambda+2\). Nosotros ojo eso\(f(2) = -8 + 3\cdot 2 + 2 = 0\). Así se\(\lambda-2\) divide\(f(\lambda)\text{;}\) para encontrar las otras raíces, realizamos la división polinómica larga:
\[ \frac{-\lambda^3+3\lambda+2}{\lambda-2} = -\lambda^2-2\lambda-1 = -(\lambda+1)^2. \nonumber \]
Por lo tanto,
\[ f(\lambda) = -(\lambda-2)(\lambda+1)^2, \nonumber \]
así que los únicos valores propios son\(\lambda = 2,-1\).
Calculamos el\(2\) espacio propio resolviendo el sistema homogéneo\((A-2I_3)x=0\). Tenemos
\[A-2I_{3}=\left(\begin{array}{ccc}-2&6&8\\ \frac{1}{2}&-2&0\\0&\frac{1}{2}&-2\end{array}\right)\quad\xrightarrow{\text{RREF}}\quad\left(\begin{array}{ccc}1&0&-16\\0&1&-4\\0&0&0\end{array}\right).\nonumber\]
La forma paramétrica y la forma vectorial paramétrica de las soluciones son:
\[\left\{\begin{array}{rrr}x&=&16z \\ y&=&4z \\ z&=&z\end{array}\right.\quad\longrightarrow\quad\left(\begin{array}{c}x\\y\\z\end{array}\right)=z\left(\begin{array}{c}16\\4\\1\end{array}\right).\nonumber\]
Por lo tanto, el\(2\) -eigenspace es la línea
\[ \text{Span}\left\{\left(\begin{array}{c}16\\4\\1\end{array}\right)\right\}. \nonumber \]
Calculamos el\(-1\) espacio propio resolviendo el sistema homogéneo\((A+I_3)x=0\). Tenemos
\[A+I_{3}=\left(\begin{array}{ccc}1&6&8\\ \frac{1}{2}&1&0\\0&\frac{1}{2}&1\end{array}\right)\quad\xrightarrow{\text{RREF}}\quad\left(\begin{array}{ccc}1&0&-4\\0&1&2\\0&0&0\end{array}\right).\nonumber\]
La forma paramétrica y la forma vectorial paramétrica de las soluciones son:
\[\left\{\begin{array}{rrr}z&=&4z\\ y&=&-2z\\ z&=&z\end{array}\right.\quad\longrightarrow\quad\left(\begin{array}{c}x\\y\\z\end{array}\right)=z\left(\begin{array}{c}4\\-2\\1\end{array}\right).\nonumber\]
Por lo tanto, el\(-1\) -eigenspace es la línea
\[ \text{Span}\left\{\left(\begin{array}{c}4\\-2\\1\end{array}\right)\right\}. \nonumber \]
Forma del polinomio característico
Es hora de que justificemos el uso del término “polinomio”. Primero necesitamos una palabra de vocabulario.
La traza de una matriz cuadrada\(A\) es el número\(\text{Tr}(A)\) obtenido sumando las entradas diagonales de\(A\text{:}\)
\[\text{Tr}\left(\begin{array}{ccccc}\color{red}{a_{11}}&\color{black}{a_{12}}&\cdots&a_{1,n-1}&a_{1n} \\ a_{21}&\color{red}{a_{22}}&\color{black}{\cdots}&a_{2,n-1}&a_{2n} \\ \vdots &\vdots &\ddots &\vdots &\vdots \\ a_{n-1,1}&a_{n-1,2}&\cdots&\color{red}{a_{n-1,n-1}}&\color{black}{a_{n-1,n}} \\ a_{n1}&a_{n2}&\cdots &a_{n,n-1}&\color{red}{a_{nn}}\end{array}\right)=\color{red}{a_{11}+a_{22}+\cdots +a_{nn}}\color{black}{.}\nonumber\]
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\(f(\lambda)=\det(A-\lambda I_n)\) ser su polinomio característico. Entonces\(f(\lambda)\) es un polinomio de grado\(n\). Además,\(f(\lambda)\) tiene la forma
\[ f(\lambda) = (-1)^n\lambda^n + (-1)^{n-1}\text{Tr}(A)\lambda^{n-1} + \cdots + \det(A). \nonumber \]
En otras palabras, el coeficiente de\(\lambda^{n-1}\) es\(\pm\text{Tr}(A)\text{,}\) y el término constante es\(\det(A)\) (los otros coeficientes son solo números sin nombres).
- Prueba
-
Primero notamos que
\[ f(0) = \det(A - 0I_n) = \det(A), \nonumber \]
para que el término constante sea siempre\(\det(A)\).
Demostraremos el resto del teorema solo para\(2\times 2\) matrices; se alienta al lector a completar la prueba en general usando expansiones de cofactores. Podemos escribir una\(2\times 2\) matriz como\(A = \left(\begin{array}{cc}a&b\\c&d\end{array}\right)\text{;}\) entonces
\[ \begin{split} f(\lambda) \amp= \det(A-\lambda I_2) = \det\left(\begin{array}{cc}a-\lambda&b\\c&d-\lambda\end{array}\right) = (a-\lambda)(d-\lambda)-bc \\ \amp=\lambda^2 - (a+d)\lambda + (ad-bc) = \lambda^2 - \text{Tr}(A)\lambda + \det(A). \end{split} \nonumber \]
Cuando\(n=2\text{,}\) el Teorema anterior nos\(\PageIndex{2}\) cuenta todos los coeficientes del polinomio característico:
\[ f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(A). \nonumber \]
Esta es generalmente la forma más rápida de calcular el polinomio característico de una\(2\times 2\) matriz.
Encuentra el polinomio característico de la matriz
\[ A = \left(\begin{array}{cc}5&2\\2&1\end{array}\right). \nonumber \]
Solución
Tenemos
\[ f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(A) = \lambda^2 - (5+1)\lambda + (5\cdot 1-2\cdot 2) = \lambda^2 - 6\lambda + 1, \nonumber \]
como en el Ejemplo anterior\(\PageIndex{1}\).
Por el Teorema anterior\(\PageIndex{2}\), el polinomio característico de una\(n\times n\) matriz es un polinomio de grado\(n\). Dado que un polinomio de grado\(n\) tiene como máximo\(n\) raíces, esto da otra prueba del hecho de que una\(n\times n\) matriz tiene como máximo\(n\) valores propios. Ver Nota 5.1.3 en la Sección 5.1.
Valores propios de una matriz triangular
Es fácil calcular el determinante de una matriz triangular superior o inferior; esto facilita encontrar también sus valores propios.
Si\(A\) es una matriz triangular superior o inferior, entonces los valores propios de\(A\) son sus entradas diagonales.
- Prueba
-
Supongamos por simplicidad que\(A\) es una matriz\(3\times 3\) triangular superior:
\[ A = \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&0&a_{33}\end{array}\right). \nonumber \]
Su polinomio característico es
\[ f(\lambda) = \det(A-\lambda I_3) = \det\left(\begin{array}{ccc}a_{11}-\lambda&a_{12}&a_{13}\\0&a_{22}-\lambda&a_{23}\\0&0&a_{33}-\lambda\end{array}\right). \nonumber \]
Esta también es una matriz triangular superior, por lo que el determinante es el producto de las entradas diagonales:
\[ f(\lambda) = (a_{11}-\lambda)(a_{22}-\lambda)(a_{33}-\lambda). \nonumber \]
Los ceros de este polinomio son exactamente\(a_{11},\,a_{22},\,a_{33}.\)
Encuentra los valores propios de la matriz
\[ A = \left(\begin{array}{cccc}1&7&2&4\\0&1&3&11\\0&0&\pi&101\\0&0&0&0\end{array}\right). \nonumber \]
Solución
Los valores propios son las entradas diagonales\(1,\pi,0\). (El valor propio\(1\) ocurre dos veces, pero cuenta como un valor propio; en la Sección 5.4 definiremos la noción de multiplicidad algebraica de un valor propio).
Factorización del polinomio característico
Si\(A\) es una\(n\times n\) matriz, entonces el polinomio característico\(f(\lambda)\) tiene grado\(n\) por el Teorema anterior\(\PageIndex{2}\). Cuando\(n=2\text{,}\) se puede utilizar la fórmula cuadrática para encontrar las raíces de\(f(\lambda)\). Existen fórmulas algebraicas para las raíces de polinomios [1]cúbicos y cuárticos, pero estas son generalmente demasiado engorrosas para aplicarlas a mano. Peor aún, se sabe que no existe una fórmula algebraica para las raíces de un polinomio general de grado al menos\(5\).
En la práctica, las raíces del polinomio característico se encuentran numéricamente por computadora. Dicho esto, sí existen métodos para encontrar raíces a mano. Por ejemplo, tenemos la siguiente consecuencia del teorema de raíz racional (que también llamamos teorema de raíz racional):
Supongamos que\(A\) es una\(n\times n\) matriz cuyo polinomio característico\(f(\lambda)\) tiene entradas enteras (números enteros). Entonces todas las raíces racionales de su polinomio característico son divisores enteros de\(\det(A)\).
Por ejemplo, si\(A\) tiene entradas enteras, entonces su polinomio característico tiene coeficientes enteros. Esto nos da una manera de encontrar una raíz a mano, si\(A\) tiene un valor propio que es un número racional. Una vez que hemos encontrado una raíz, entonces podemos reducir el grado por división polinómica larga.
Encuentra los valores propios de la matriz
\[ A = \left(\begin{array}{ccc}7&0&3\\-3&2&-3\\-3&0&-1\end{array}\right). \nonumber \]
Pista: un valor propio es un entero.
Solución
Calculamos el polinomio característico expandiendo cofactores a lo largo de la primera fila:
\[ \begin{split} f(\lambda) = \det(A - \lambda I_3) \amp= \det\left(\begin{array}{ccc}7-\lambda&0&3\\-3&2-\lambda&-3\\-3&0&-1-\lambda\end{array}\right) \\ \amp= (7-\lambda)(2-\lambda)(-1-\lambda) + 3\cdot 3(2-\lambda) \\ \amp= -\lambda^3 + 8\lambda^2 - 14\lambda + 4. \end{split} \nonumber \]
El determinante de\(A\) es el término constante que son\(f(0) = 4\text{;}\) sus divisores enteros\(\pm 1,\pm 2,\pm 4\). Comprobamos cuáles son las raíces:
\[ f(1) = -3 \quad f(-1) = 27 \quad f(2) = 0 \quad f(-2) = 72 \quad f(4) = 12 \quad f(-4) = 252. \nonumber \]
La única raíz racional de\(f(\lambda)\) es\(\lambda=2\). Dividimos mediante\(\lambda-2\) el uso de la división polinómica larga:
\[ \frac{-\lambda^3 + 8\lambda^2 - 14\lambda + 4}{\lambda-2} = -\lambda^2 + 6\lambda - 2. \nonumber \]
Podemos usar la fórmula cuadrática para encontrar las raíces del cociente:
\[ \lambda = \frac{-6 \pm\sqrt{36 - 4\cdot 2}}{-2} = 3\pm\sqrt 7. \nonumber \]
Hemos factorizado\(f\) completamente:
\[ f(\lambda) = -(\lambda-2)\bigl(\lambda-(3+\sqrt7)\bigr)\bigl(\lambda-(3-\sqrt7)\bigr). \nonumber \]
Por lo tanto, los valores propios de\(A\) son\(2,\,3+\sqrt7,\,3-\sqrt7.\)
En el ejemplo anterior, podríamos haber expandido cofactores a lo largo de la segunda columna para obtener
\[ f(\lambda) = (2-\lambda)\det\left(\begin{array}{cc}7-\lambda&3\\-3&-1-\lambda\end{array}\right). \nonumber \]
Dado que\(2-\lambda\) era la única entrada distinta de cero en su columna, esta expresión ya tiene el\(2-\lambda\) término factorizado: el teorema de raíz racional no era necesario. El determinante en la expresión anterior es el polinomio característico de la matriz\(\left(\begin{array}{cc}7&3\\-3&-1\end{array}\right)\text{,}\) para que podamos calcularlo usando la traza y el determinante:
\[ f(\lambda) = (2-\lambda)\bigl(\lambda^2-(7-1)\lambda+(-7+9)\bigr) = (2-\lambda)(\lambda^2-6\lambda+2). \nonumber \]
Encuentra los valores propios de la matriz
\[ A = \left(\begin{array}{ccc}7&0&3\\-3&2&-3\\4&2&0\end{array}\right). \nonumber \]
Solución
Calculamos el polinomio característico expandiendo cofactores a lo largo de la primera fila:
\[ \begin{split} f(\lambda) = \det(A - \lambda I_3) \amp= \det\left(\begin{array}{ccc}7-\lambda&0&3\\-3&2-\lambda&-3\\4&2&-\lambda\end{array}\right) \\ \amp= (7-\lambda)\bigl(-\lambda(2-\lambda)+6\bigr) + 3\bigl(-6-4(2-\lambda)\bigr) \\ \amp= -\lambda^3 + 9\lambda^2 - 8\lambda. \end{split} \nonumber \]
El término constante es cero, por lo que\(A\) tiene determinante cero. Factorizamos\(\lambda\text{,}\) luego globo ocular las raíces del factor cuadrático:
\[ f(\lambda) = -\lambda(\lambda^2-9\lambda+8) = -\lambda(\lambda-1)(\lambda-8). \nonumber \]
Por lo tanto, los valores propios de\(A\) son\(0,1,\) y\(8\).
\(A\)Déjese ser una\(n\times n\) matriz. Aquí hay algunas estrategias para factorizar su polinomio característico\(f(\lambda)\). Primero, debes encontrar un valor propio:
- ¡No multipliques el polinomio característico si ya está parcialmente factorizado! Esto sucede si expandes cofactores a lo largo de la segunda columna en este Ejemplo\(\PageIndex{7}\).
- Si no hay término constante, se puede factorizar\(\lambda\text{,}\) como en este Ejemplo\(\PageIndex{8}\).
- Si la matriz es triangular, las raíces son las entradas diagonales.
- Adivina un valor propio usando el Teorema\(\PageIndex{3}\): si\(\det(A)\) es un entero, sustituya todos los divisores (positivos y negativos) de\(\det(A)\) en\(f(\lambda)\).
- Encuentra un valor propio usando la geometría de la matriz. Por ejemplo, una reflexión, Ejemplo 5.1.4 en la Sección 5.1, tiene valores propios\(\pm 1\).
Después de obtener un valor propio,\(\lambda_1\text{,}\) utilice la división polinómica larga para calcular\(f(\lambda)/(\lambda-\lambda_1)\). Este polinomio tiene menor grado. Si\(n=3\) entonces se trata de un polinomio cuadrático, al que se le puede aplicar la fórmula cuadrática para encontrar las raíces restantes.


