5.3: Similaridad

Objetivos

1. Aprende a interpretar geoemétricamente matrices similares.
2. Comprender la relación entre los valores propios, los vectores propios y los polinomios característicos de matrices similares.
3. Receta: computar\(Ax\) en términos de\(B\),\(C\) para\(A=CBC^{−1}\).
4. Imagen: la geometría de matrices similares.
5. Vocabulario palabra: similitud.

Algunas matrices son fáciles de entender. Por ejemplo, una matriz diagonal

\[D=\left(\begin{array}{cc}2&0\\0&1/2\end{array}\right)\nonumber\]

simplemente escala las coordenadas de un vector:\(D\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}2x\\ y/2\end{array}\right)\). El propósito de la mayor parte del resto de este capítulo es comprender matrices de aspecto complicado analizando hasta qué punto “se comportan” como matrices simples. Por ejemplo, la matriz

\[A=\frac{1}{10}\left(\begin{array}{cc}11&6\\9&14\end{array}\right)\nonumber\]

tiene valores propios\(2\) y\(1/2\), con vectores propios correspondientes\(v_1=\left(\begin{array}{c}2/3\\1\end{array}\right)\) y\(v_{2}=\left(\begin{array}{c}−1\\1\end{array}\right)\). Observe que

\[\begin{aligned}D(xe_{1}+ye_{2})=&xDe_{1}+yDe_{2}=2xe_{1}−\frac{1}{2}ye_{2} \\ A(xv_{1}+yv_{2})&=xAv_{1}+yAv_{2}=2xv_{1}−\frac{1}{2}yv_{2}.\end{aligned}\]

Usar\(v_{1},\: v_{2}\) en lugar de las coordenadas habituales hace que\(A\) “se comporte” como una matriz diagonal.

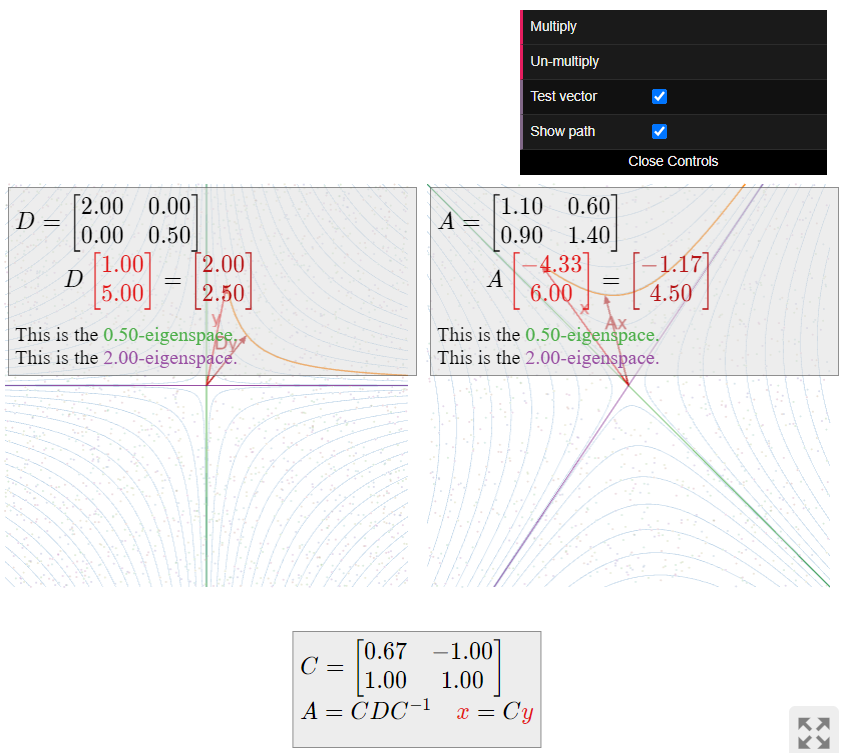
Figura\(\PageIndex{1}\): Las matrices\(A\) y\(D\) se comportan de manera similar. Haga clic en “multiplicar” para multiplicar los puntos\(D\) coloreados por a la\(A\) izquierda y a la derecha. (Veremos en la Sección 5.4 por qué los puntos siguen caminos hiperbólicos.)

El otro caso de particular importancia serán las matrices que “se comporten” como una matriz de rotación: en efecto, esto será crucial para entender la Sección 5.5 geométricamente. Ver Nota\(\PageIndex{3}\).

En esta sección, estudiamos en detalle la situación cuando dos matrices se comportan de manera similar con respecto a diferentes sistemas de coordenadas. En la Sección 5.4 y la Sección 5.5, mostraremos cómo usar valores propios y vectores propios para encontrar una matriz más simple que se comporte como una matriz dada.

Matrices Similares

Comenzamos con la definición algebraica de similitud.

Definición \(\PageIndex{1}\): Similar

Dos\(n\times n\) matrices\(A\) y\(B\) son similares si existe una\(n\times n\) matriz invertible\(C\) tal que\(A=CBC^{−1}\).

Ejemplo\(\PageIndex{1}\)

Las matrices

\[\left(\begin{array}{cc}-12&15\\-10&13\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}3&0\\0&-2\end{array}\right)\nonumber\]

son similares porque

\[\left(\begin{array}{cc}-12&15\\-10&13\end{array}\right)=\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)\left(\begin{array}{cc}3&0\\0&-2\end{array}\right)\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)^{-1},\nonumber\]

como puede verificar el lector.

Ejemplo\(\PageIndex{2}\)

Las matrices

\[\left(\begin{array}{cc}3&0\\0&-2\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\nonumber\]

no son similares. En efecto, la segunda matriz es la matriz de identidad\(I_{2}\), así que si\(C\) es alguna\(2\times 2\) matriz invertible, entonces

\[CI_{2}C^{-1}=CC^{-1}=I_{2}\neq\left(\begin{array}{cc}3&0\\0&-2\end{array}\right).\nonumber\]

Al igual que en el ejemplo anterior, se puede mostrar que\(I_{n}\) es la única matriz que es similar a\(I_{n}\), e igualmente para cualquier múltiplo escalar de\(I_{n}\).

Nota \(\PageIndex{1}\)

La similitud no está relacionada con la equivalencia de filas. Cualquier matriz invertible es fila equivalente a\(I_{n}\), pero\(I_{n}\) es la única matriz similar a\(I_{n}\). Por ejemplo,

\[\left(\begin{array}{cc}2&1\\0&2\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\nonumber\]

son equivalentes de fila pero no similares.

Como sugiere su nombre, la similitud es lo que se llama una relación de equivalencia. Esto significa que satisface las siguientes propiedades.

Proposición \(\PageIndex{1}\)

Dejar\(A\),\(B\), y\(C\) ser\(n\times n\) matrices.

1. Reflexivity:\(A\) es similar a sí mismo.
2. Simetría: si\(A\) es similar a\(B\), entonces\(B\) es similar a\(A\).
3. Transitividad: si\(A\) es similar a\(B\) y\(B\) es similar a\(C\), entonces\(A\) es similar a\(C\).

Prueba

1. Tomando\(C=I_{n}=I_{n}^{−1}\), tenemos\(A=I_{n}AI_{n}^{−1}\).
2. Supongamos que\(A=CBC^{−1}\). Multiplicando ambos lados a la izquierda por\(C^{−1}\) y a la derecha por\(C\) da\[C^{−1}AC=C^{−1}(CBC^{−1})C=B.\nonumber\] Since\((C^{−1})^{−1}=C\), tenemos\(B=C^{−1}A(C^{−1})^{−1}\), así que eso\(B\) es similar a\(A\).
3. Supongamos que\(A=DBD^{−1}\) y\(B=ECE^{−1}\). Subsituando\(B\) y recordando eso\((DE)^{−1}=E^{−1}D^{−1}\), tenemos\[A=D(ECE^{−1})D^{−1}=(DE)C(DE)^{−1},\nonumber\] lo que demuestra que\(A\) es similar a\(C\).

Ejemplo\(\PageIndex{3}\)

Las matrices

\[\left(\begin{array}{cc}-12&15\\-10&13\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}3&0\\0&-2\end{array}\right)\nonumber\]

son similares, como vimos en Ejemplo\(\PageIndex{1}\). Asimismo, las matrices

\[\left(\begin{array}{cc}-12&15\\-10&13\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}-12&5\\-30&13\end{array}\right)\nonumber\]

son similares porque

\[\left(\begin{array}{cc}-12&5\\-30&13\end{array}\right)=\left(\begin{array}{cc}2&-1\\2&1\end{array}\right)\left(\begin{array}{cc}-12&15\\-10&13\end{array}\right)\left(\begin{array}{cc}2&-1\\2&1\end{array}\right)^{-1}.\nonumber\]

De ello se deduce que

\[\left(\begin{array}{cc}-12&5\\-30&13\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}3&0\\0&-2\end{array}\right)\nonumber\]

son similares entre sí.

Concluimos con una observación sobre la similitud y los poderes de las matrices.

Hecho \(\PageIndex{1}\)

Vamos\(A=CBC^{-1}\). Entonces para cualquiera\(n\geq 1\), tenemos

\[A^{n}=CB^{n}C^{-1}.\nonumber\]

Prueba

Primero tenga en cuenta que

\[A^{2}=AA=(CBC^{−1})(CBC^{−1})=CB(C^{−1}C)BC^{−1}=CBI_{n}BC^{−1}=CB^{2}C^{−1}.\nonumber\]

A continuación tenemos

\[A^{3}=A^{2}A=(CB^{2}C^{−1})(CBC^{−1})=CB^{2}(C^{−1}C)BC^{−1}=CB^{3}C^{−1}.\nonumber\]

El patrón es claro.

Ejemplo\(\PageIndex{4}\)

Computar\(A^{100}\), donde

\[A=\left(\begin{array}{cc}5&13\\-2&-5\end{array}\right)=\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)\left(\begin{array}{cc}0&-1\\1&0\end{array}\right)\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)^{-1}.\nonumber\]

Solución

Por el hecho\(\PageIndex{1}\), tenemos

\[A^{100}=\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)\left(\begin{array}{cc}0&-1\\1&0\end{array}\right)^{100}\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)^{-1}.\nonumber\]

La matriz\(\left(\begin{array}{cc}0&-1\\1&0\end{array}\right)\) es una rotación en sentido antihorario por\(90^{\circ}\). Si giramos\(90^{\circ}\) cuatro veces, entonces terminamos por donde empezamos. De ahí que rotar\(90^{\circ}\) cien veces es la transformación de la identidad, por lo que

\[A^{100}=\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\left(\begin{array}{c}-2&3\\1&-1\end{array}\right)^{-1}=\left(\begin{array}{cc}1&0\\0&1\end{array}\right).\nonumber\]

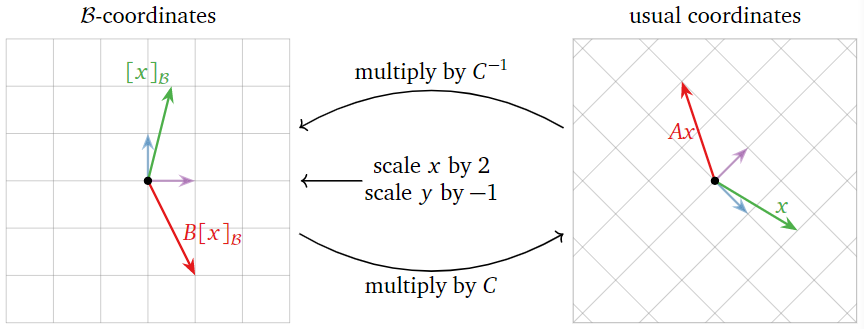
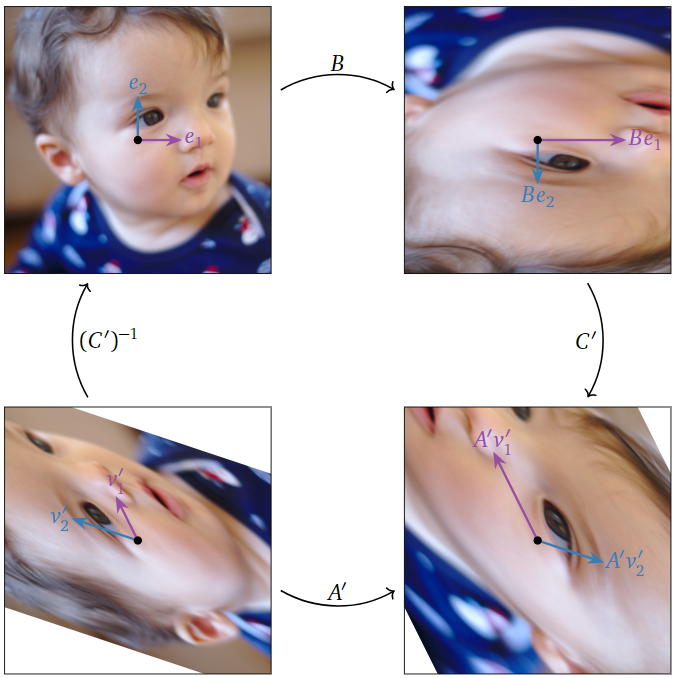
Geometría de Matrices Similares

La similitud es una construcción muy interesante cuando se ve geométricamente. Veremos que, aproximadamente, matrices similares hacen lo mismo en diferentes sistemas de coordenadas. El lector podría querer revisar\(\mathcal{B}\) -coordenadas y cuadrículas de coordenadas no estándar en la Sección 2.8 antes de leer esta subsección.

Por las condiciones 4 y 5 del teorema de la matriz invertible en la Sección 5.1, una\(n\times n\) matriz\(C\) es invertible si y solo si sus columnas\(v_{1},\:v_{2},\cdots ,v_{n}\) forman una base para\(\mathbb{R}^{n}\). Esto significa que podemos hablar de las\(\mathcal{B}\) -coordenadas de un vector en\(\mathbb{R}^{n}\), donde\(\mathcal{B}\) está la base de columnas de\(C\). Recordemos que

\[ [x]_{\mathcal{B}}=\left(\begin{array}{c}c_1 \\ c_2 \\ \vdots \\ c_n\end{array}\right)\quad\text{means}\quad x=c_1v_1+c_2v_2+\cdots +c_nv_n=\left(\begin{array}{cccc}|&|&\quad&| \\ v_1&v_2&\cdots&v_n \\ |&|&\quad&|\end{array}\right)\left(\begin{array}{c}c_1\\c_2\\ \vdots \\ c_n\end{array}\right).\nonumber\]

Ya que\(C\) es la matriz con columnas\(v_1,\:v_2,\cdots, v_n\), esto dice eso\(x=C[x]_{\mathcal{B}}\). Multiplicando ambos lados por\(C^{−1}\) da\([x]_{\mathcal{B}}=C^{−1}x\). Para resumir:

Nota \(\PageIndex{2}\)

Dejar\(C\) ser una\(n\times n\) matriz invertible con columnas\(v_1,\:v_2,\cdots ,v_n\), y dejar\(\mathcal{B}=\{v_1,\:v_2,\cdots ,v_n\}\), una base para\(\mathbb{R}^{n}\). Entonces para cualquiera\(x\) en\(\mathbb{R}^{n}\), tenemos

\[C[x]_{\mathcal{B}}=x\quad\text{and}\quad C^{-1}x=[x]_{\mathcal{B}}.\nonumber\]

Esto dice que\(C\) cambia de las\(\mathcal{B}\) coordenadas -a las coordenadas habituales, y\(C^{−1}\) cambia de las coordenadas habituales a las\(\mathcal{B}\) coordenadas -coordenadas.

Supongamos que\(A=CBC^{−1}\). La observación anterior nos da otra forma de calcular\(Ax\) para un vector\(x\) en\(\mathbb{R}^{n}\). Recordemos eso\(CBC^{−1}x=C(B(C^{−1}x))\), para que multiplicar\(CBC^{−1}\) por\(x\) medios primero multiplicando por\(C^{−1}\), luego por\(B\), luego por\(C\). Ver Ejemplo 3.4.10 en la Sección 3.4.

Receta: Computación\(Ax\) in terms of \(B\).

Supongamos que\(A=CBC^{−1}\), donde\(C\) está una matriz invertible con columnas\(v_{1},\:v_{2},\cdots ,v_n\). Vamos\(\mathcal{B}=\{v_1,\:v_2,\cdots ,v_n\}\), una base para\(\mathbb{R}^{n}\). Dejar\(x\) ser un vector en\(\mathbb{R}^{n}\). Para calcular\(Ax\), uno hace lo siguiente:

1. Multiplicar\(x\) por\(C^{−1}\), que cambia a las\(\mathcal{B}\) coordenadas -:\([x]_{\mathcal{B}}=C^{−1}x\).
2. Multiplique esto por\(B\):\(B[x]_{\mathcal{B}}=BC^{−1}x\).
3. Interpretando este vector como un vector\(\mathcal{B}\) -coordenada, lo multiplicamos por\(C\) para volver a cambiar a las coordenadas habituales:\(Ax=CBC^{−1}x=CB[x]_{\mathcal{B}}\).

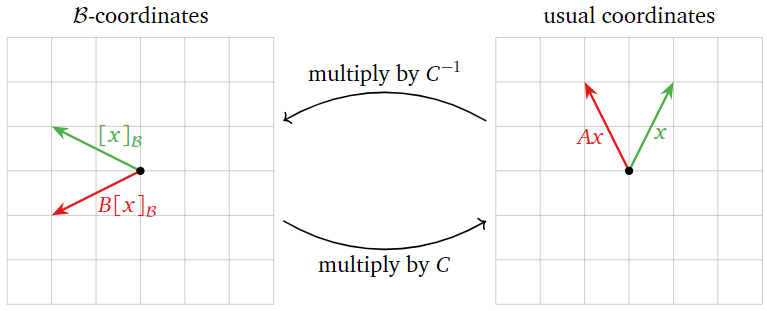
Figura\(\PageIndex{2}\)

Para resumir: si\(A=CBC^{-1}\), entonces\(A\) y\(B\) hacer lo mismo, sólo en diferentes sistemas de coordenadas.

El siguiente ejemplo es el corazón de esta sección.

Ejemplo\(\PageIndex{5}\)

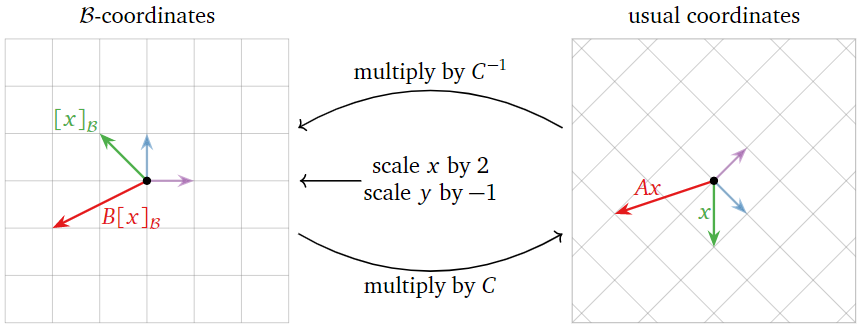
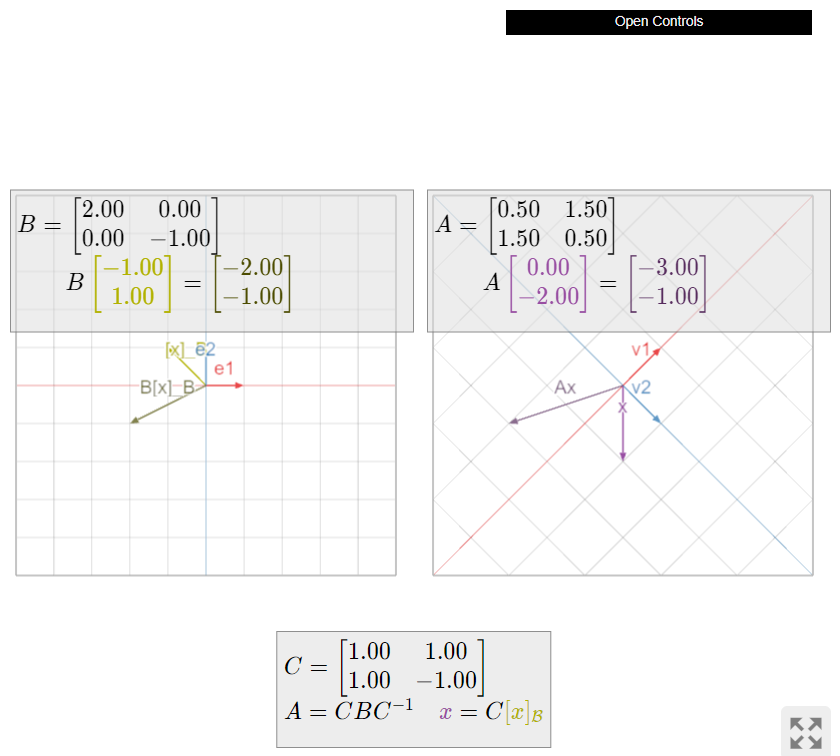
Considerar las matrices

\[A=\left(\begin{array}{cc}1/2&3/2\\ 3/2&1/2\end{array}\right)\quad B=\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)\quad C=\left(\begin{array}{cc}1&1\\1&-1\end{array}\right).\nonumber\]

Se puede verificar que\(A=CBC^{−1}\): vea el Ejemplo 5.4.1 en la Sección 5.4. Dejar\(v_{1}=\left(\begin{array}{c}1\\1\end{array}\right)\) y\(v_2=\left(\begin{array}{c}1\\-1\end{array}\right)\), las columnas de\(C\), y dejar\(\mathcal{B}=\{v_1,\:v_2\}\), una base de\(\mathbb{R}^{2}\).

La matriz\(B\) es diagonal: escala la\(x\) -dirección por un factor de\(2\) y la\(y\) -dirección por un factor de\(−1\).

Figura\(\PageIndex{3}\)

Para calcular\(Ax\), primero multiplicamos por\(C^{−1}\) para encontrar las\(\mathcal{B}\) -coordenadas de\(x\), luego multiplicamos por\(B\), luego multiplicamos por\(C\) otra vez. Por ejemplo, vamos\(\color{Green}{x}\color{black}{=\left(\begin{array}{c}0\\-2\end{array}\right)}\).

1. Vemos desde la cuadrícula\(\mathcal{B}\) -coordenada debajo de eso\(\color{Green}{x}\color{black}{=−}\color{Purple}{v_{1}}\color{black}{+}\color{blue}{v_{2}}\). Por lo tanto,\(C^{−1}\color{Green}{x}\color{black}{=}\color{Green}{[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}-1\\1\end{array}\right)}\)..
2. Multiplicando por\(B\) escalas las coordenadas:\(\color{red}{B[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}-2\\-1\end{array}\right)}\).
3. Interpretando\(\left(\begin{array}{c}-2\\-1\end{array}\right)\) como un vector\(\mathcal{B}\) -coordenada, multiplicamos por\(C\) para obtener

\[\color{red}{Ax}\color{black}{=C\left(\begin{array}{c}-2\\-1\end{array}\right)=-2}\color{Purple}{v_{1}}\color{black}{-}\color{blue}{v_{2}}\color{black}{=\left(\begin{array}{c}-3\\-1\end{array}\right).}\nonumber\]

Por supuesto, este vector se encuentra\((−2,−1)\) en la cuadrícula\(\mathcal{B}\) -coordenada.

Figura\(\PageIndex{4}\)

Ahora vamos\(\color{Green}{x}\color{black}{=\frac{1}{2}\left(\begin{array}{c}5\\-3\end{array}\right)}\).

1. Vemos desde la cuadrícula\(\mathcal{B}\) -coordenada que\(\color{Green}{x}\color{black}{=\frac{1}{2}}\color{Purple}{v_{1}}\color{black}{+2}\color{blue}{v_{2}}\). Por lo tanto,\(C^{−1}\color{Green}{x}\color{black}{=}\color{Green}{[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}1/2 \\ 2\end{array}\right)}\).
2. Multiplicando por\(B\) escalas las coordenadas:\(\color{Red}{B[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}1\\-2\end{array}\right)}\).
3. Interpretando\(\left(\begin{array}{c}1\\-2\end{array}\right)\) como un vector\(\mathcal{B}\) -coordenada, multiplicamos por\(C\) para obtener

\[\color{Red}{Ax}\color{black}{=C\left(\begin{array}{c}1\\-2\end{array}\right)=}\color{Purple}{v_{1}}\color{black}{-2}\color{blue}{v_{2}}\color{black}{=\left(\begin{array}{c}-1\\3\end{array}\right).}\nonumber\]

Este vector se encuentra\((1,−2)\) en la cuadrícula\(\mathcal{B}\) -coordenada.

Figura\(\PageIndex{5}\)

Para resumir:

• \(B\)escala la\(e_1\) -dirección por\(2\) y la\(e_2\) -dirección por\(-1\).
• \(A\)escala la\(v_1\) -dirección por\(2\) y la\(v_2\) -dirección por\(-1\).

Figura\(\PageIndex{6}\)

Figura\(\PageIndex{7}\): La relación geométrica entre las matrices similares\(A\) y la\(B\) actuación sobre ellas\(\mathbb{R}^2\). Haga clic y arrastre las cabezas de\(x\) y\([x]_{\mathcal{B}}\). Estudia esta imagen hasta que puedas predecir de manera confiable dónde estarán los otros tres vectores después de mover uno de ellos: esta es la esencia de la geometría de matrices similares.

Ejemplo\(\PageIndex{6}\): Interactive: Another matrix similar to \(B\)

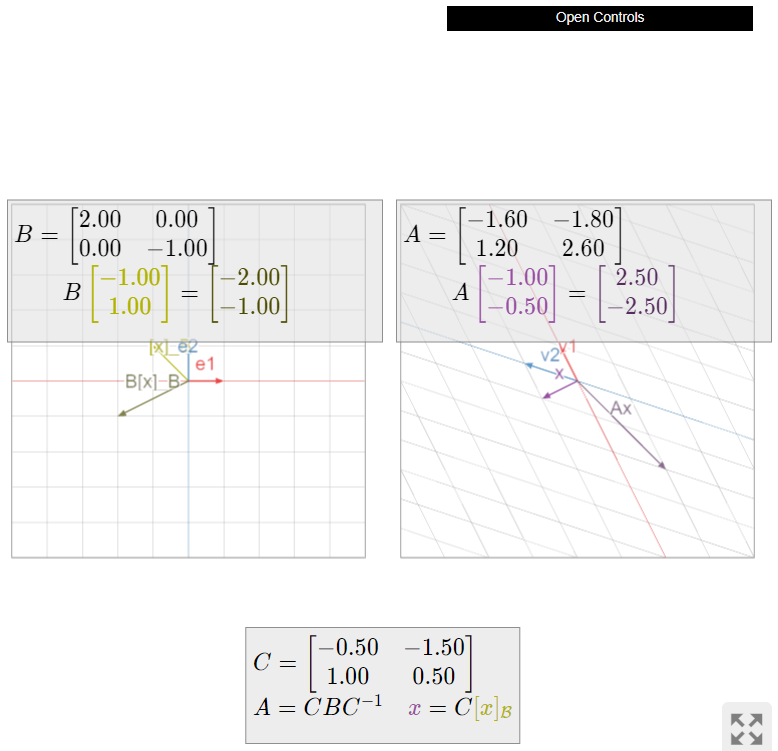
Considerar las matrices

\[A'=\frac{1}{5}\left(\begin{array}{cc}-8&-9\\6&13\end{array}\right)\quad B=\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)\quad C'=\frac{1}{2}\left(\begin{array}{cc}-1&-3\\2&1\end{array}\right).\nonumber\]

Entonces\(A'=C'B(C')^{−1}\), como se puede verificar. Dejar\(v_1'=\frac{1}{2}\left(\begin{array}{c}-1\\2\end{array}\right)\) y\(v_2'=\frac{1}{2}\left(\begin{array}{c}-3\\1\end{array}\right)\), las columnas de\(C'\), y dejar\(\mathcal{B}'=\{v_1',v_2'\}\). Entonces\(A'\) hace lo mismo que\(B\), como en el ejemplo anterior\(\PageIndex{5}\), excepto que\(A'\) usa el sistema\(\mathcal{B}'\) -coordinate. En otras palabras:

• \(B\)escala la\(e_1\) -dirección por\(2\) y la\(e_2\) -dirección por\(-1\).
• \(A'\)escala la\(v_1'\) -dirección por\(2\) y la\(v_2'\) -dirección por\(-1\).

Figura\(\PageIndex{8}\)

Figura\(\PageIndex{9}\): La relación geométrica entre las matrices similares\(A'\) y la\(B\) actuación sobre ellas\(\mathbb{R}^2\). Haga clic y arrastre las cabezas de\(x\) y\([x]_{\mathcal{B}'}\).

Ejemplo\(\PageIndex{7}\): A matrix similar to a rotation matrix

Considerar las matrices

\[A=\frac{1}{6}\left(\begin{array}{cc}7&-17\\5&-7\end{array}\right)\quad B=\left(\begin{array}{cc}0&-1\\1&0\end{array}\right)\quad C=\left(\begin{array}{cc}2&-1/2 \\ 1&1/2\end{array}\right).\nonumber\]

Uno puede verificar eso\(A=CBC^{−1}\). Dejar\(v_{1}=\left(\begin{array}{c}2\\1\end{array}\right)\) y\(v_2=\frac{1}{2}\left(\begin{array}{c}-1\\1\end{array}\right)\), las columnas de\(C\), y dejar\(\mathcal{B}=\{v_1,v_2\}\), una base de\(\mathbb{R}^2\).

La matriz\(B\) gira el plano en sentido contrario a las agujas del reloj\(90^{\circ}\).

Figura\(\PageIndex{10}\)

Para calcular\(Ax\), primero multiplicamos por\(C^{−1}\) para encontrar las\(\mathcal{B}\) -coordenadas de\(x\), luego multiplicamos por\(B\), luego multiplicamos por\(C\) otra vez. Por ejemplo, vamos\(\color{Green}{x}\color{black}{=\frac{3}{2}\left(\begin{array}{c}1\\1\end{array}\right)}\).

1. Vemos desde la cuadrícula\(\mathcal{B}\) -coordenada debajo de eso\(\color{Green}{x}\color{black}{=}\color{Purple}{v_{1}}\color{black}{+}\color{blue}{v_{2}}\). Por lo tanto,\(C^{−1}\color{Green}{x}\color{black}{=}\color{Green}{[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}1\\1\end{array}\right)}\).
2. Multiplicar por\(B\) rota por\(90^{\circ}\):\(\color{Red}{B[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}-1\\1\end{array}\right)}\).
3. Interpretando\(\left(\begin{array}{c}-1\\1\end{array}\right)\) como un vector\(\mathcal{B}\) -coordenada, multiplicamos por\(C\) para obtener

\[\color{Red}{Ax}\color{black}{=C\left(\begin{array}{c}-1\\1\end{array}\right)=-}\color{Purple}{v_{1}}\color{black}{+}\color{blue}{v_{2}}\color{black}{=\frac{1}{2}\left(\begin{array}{c}-5\\1\end{array}\right).}\nonumber\]

Por supuesto, este vector se encuentra\((-1,1)\) en la cuadrícula\(\mathcal{B}\) -coordenada.

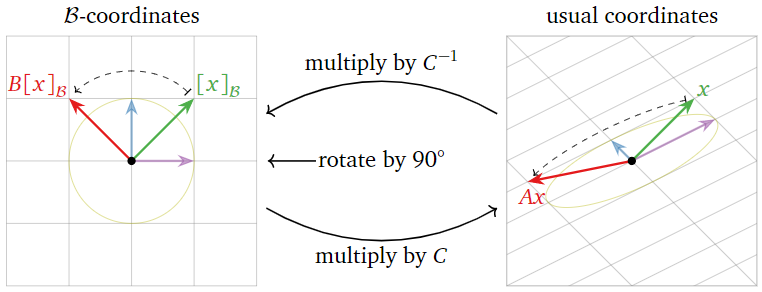
Figura\(\PageIndex{11}\)

Ahora vamos\(\color{Green}{x}\color{black}{=\frac{1}{2}\left(\begin{array}{c}-1\\-2\end{array}\right)}\).

1. Vemos desde la cuadrícula\(\mathcal{B}\) -coordenada que\(\color{Green}{x}\color{black}{=−\frac{1}{2}}\color{Purple}{v_{1}}\color{black}{−}\color{blue}{v_{2}}\). Por lo tanto,\(C^{−1}\color{Green}{x}\color{black}{=}\color{Green}{[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}-1/2 \\ -1\end{array}\right)}\).
2. Multiplicar por\(B\) rota por\(90^{\circ}\):\(\color{Red}{B[x]_{\mathcal{B}}}\color{black}{=\left(\begin{array}{c}1\\ -1/2\end{array}\right)}\).
3. Interpretando\(\left(\begin{array}{c}1\\-1/2\end{array}\right)\) como un vector\(\mathcal{B}\) -coordenada, multiplicamos por\(C\) para obtener

\[\color{Red}{Ax}\color{black}{=C\left(\begin{array}{c}1\\-1/2\end{array}\right)=}\color{Purple}{v_{1}}\color{black}{-\frac{1}{2}}\color{blue}{v_{2}}\color{black}{=\frac{1}{4}\left(\begin{array}{c}9\\3\end{array}\right).}\nonumber\]

Este vector se encuentra\((1,-\frac{1}{2})\) en la cuadrícula\(\mathcal{B}\) -coordenada.

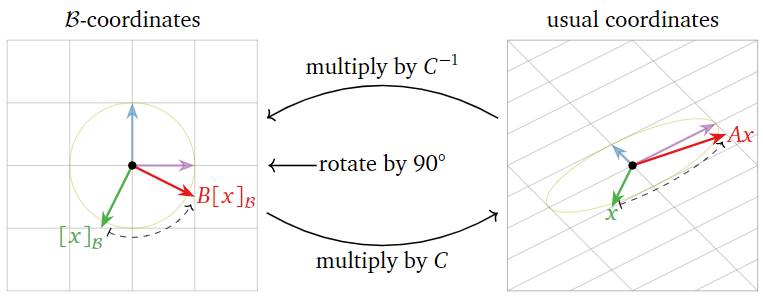
Figura\(\PageIndex{12}\)

Para resumir:

• \(B\)gira en sentido antihorario alrededor del círculo centrado en el origen y pasando por\(e_1\) y\(e_2\).
• \(A\)gira en sentido antihorario alrededor de la elipse centrada en el origen y pasando a través de\(v_1\) y\(v_2\).

Figura\(\PageIndex{13}\)

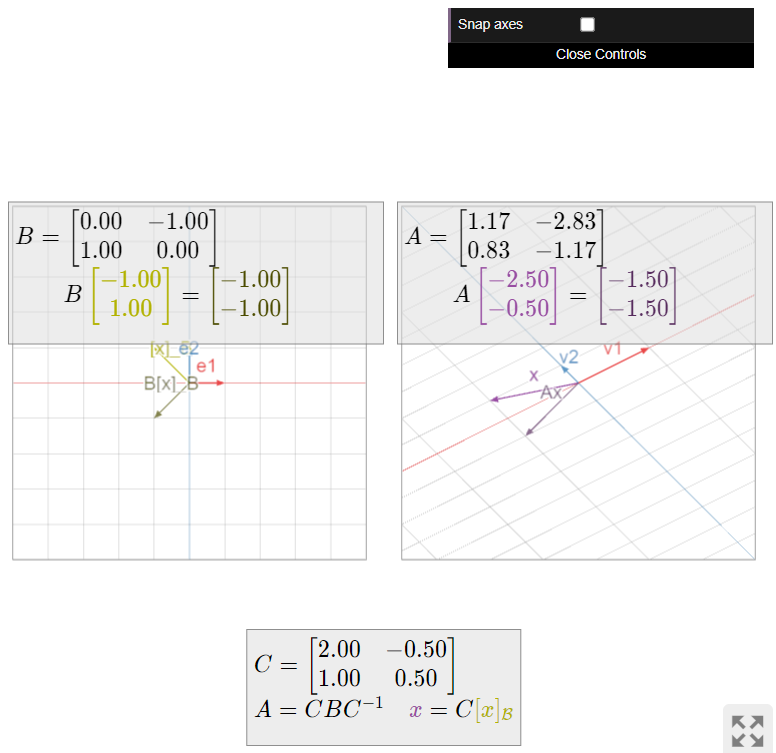
Figura\(\PageIndex{14}\): La relación geométrica entre las matrices similares\(A\) y la\(B\) actuación sobre ellas\(\mathbb{R}^2\). Haga clic y arrastre las cabezas de\(x\) y\([x]_{\mathcal{B}}\).

Para resumir y generalizar el ejemplo anterior:

Nota \(\PageIndex{3}\)

Let

\[B=\left(\begin{array}{cc}\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end{array}\right)\quad C=\left(\begin{array}{cc}|&|\\v_1&v_2\\ |&|\end{array}\right)\quad A=CBC^{-1},\nonumber\]

donde\(C\) se asume invertible. Entonces:

• \(B\)gira el plano en un ángulo de\(\theta\) alrededor del círculo centrado en el origen y que pasa a través\(e_1\) y\(e_2\), en la dirección de\(e_1\) a\(e_2\).
• \(A\)gira el plano en un ángulo de\(\theta\) alrededor de la elipse centrada en el origen y pasando a través\(v_1\) y\(v_2\), en la dirección de\(v_1\) a\(v_2\).

Figura\(\PageIndex{15}\)

Ejemplo\(\PageIndex{8}\): Interactive: Similar \(3\times 3\) matrices

Considerar las matrices

\[A=\left(\begin{array}{ccc}-1&0&0\\-1&0&2\\-1&1&1\end{array}\right)\quad B=\left(\begin{array}{ccc}-1&0&0\\0&-1&0\\0&0&2\end{array}\right)\quad C=\left(\begin{array}{ccc}-1&1&0\\1&1&1\\-1&0&1\end{array}\right).\nonumber\]

Entonces\(A=CBC^{−1}\), como se puede verificar. \(v_1,\: v_2,\: v_3\)Dejen ser las columnas de\(C\), y dejar\(\mathcal{B}=\{v_1,\: v_2,\: v_3\}\), una base de\(\mathbb{R}^3\). Entonces\(A\) hace lo mismo que\(B\), excepto\(A\) usa el sistema\(\mathcal{B}\) -coordinate. En otras palabras:

• \(B\)escala el\(e_1\),\(e_2\) -plano por\(-1\) y la\(e_3\) -dirección por\(2\).
• \(A\)escala el\(v_1\),\(v_2\) -plano por\(-1\) y la\(v_3\) -dirección por\(2\).

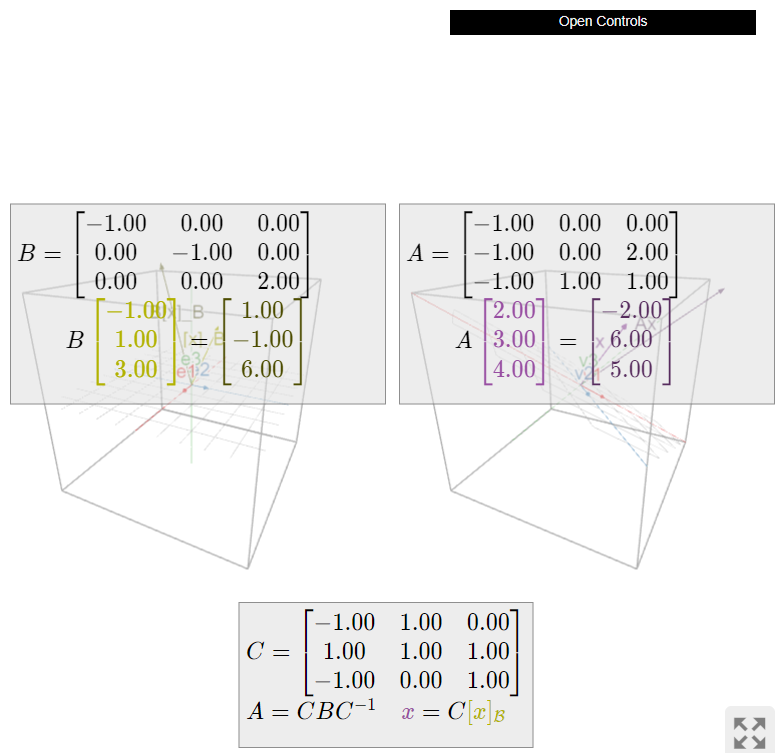
Figura\(\PageIndex{16}\): La relación geométrica entre las matrices similares\(A\) y la\(B\) actuación sobre ellas\(\mathbb{R}^3\). Haga clic y arrastre las cabezas de\(x\) y\([x]_{\mathcal{B}}\).

Valores propios de Matrices Similares

Dado que las matrices similares se comportan de la misma manera con respecto a diferentes sistemas de coordenadas, debemos esperar que sus valores propios y vectores propios estén estrechamente relacionados.

Hecho \(\PageIndex{2}\)

Matrices similares tienen el mismo polinomio característico.

Prueba

Supongamos que\(A=CBC^{−1}\)\(A\), donde\(B\),,\(C\) son\(n\times n\) matrices. Calculamos

\[\begin{aligned}A-\lambda I_{n}&=CBC^{-1}-\lambda CC^{-1}=CBC^{-1}-C\lambda C^{-1} \\ &=CBC^{-1}-C\lambda I_{n}C^{-1}=C(B_\lambda I_{n})C^{-1}.\end{aligned}\]

Por lo tanto,

\[\det(A-\lambda I_{n})=\det(C(B-\lambda I_{n})C^{-1})=\det(C)\det(B-\lambda I_{n})\det(C)^{-1}=\det(B-\lambda I_{n}).\nonumber\]

Aquí hemos utilizado la propiedad de multiplicatividad Proposición 4.1.3 en la Sección 4.1 y su Corolario 4.1.2 en la Sección 4.1.

Dado que los valores propios de una matriz son las raíces de su polinomio característico, hemos mostrado:

Nota \(\PageIndex{4}\)

Matrices similares tienen los mismos valores propios.

Por Teorema 5.2.2 en la Sección 5.2, matrices similares también tienen la misma traza y determinante.

Nota \(\PageIndex{5}\)

Lo contrario de hecho\(\PageIndex{2}\) es falso. En efecto, las matrices

\[\left(\begin{array}{cc}1&1\\0&1\end{array}\right)\quad\text{and}\quad\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\nonumber\]

ambos tienen el polinomio característico\(f(\lambda)=(\lambda -1)^{2}\), pero no son similares, porque la única matriz que es similar a\(I_2\) es\(I_2\) en sí misma.

Dado que matrices similares tienen los mismos valores propios, se podría adivinar que también tienen los mismos vectores eigen. Al reflexionar, esto no es lo que uno debe esperar: de hecho, los vectores propios solo deben coincidir después de cambiar de un sistema de coordenadas a otro. Este es el contenido del siguiente hecho, recordando eso\(C\) y\(C^{−1}\) cambiar entre las coordenadas habituales y las\(\mathcal{B}\) -coordenadas.

Hecho \(\PageIndex{3}\)

Supongamos que\(A=CBC^{-1}\). Entonces

\[\begin{array}{lll}v\text{ is an eigenvector of }A&\implies& C^{-1}v\text{ is an eigenvector of }B \\ v\text{is an eigenvector of }B&\implies & Cv\text{ is an eigenvector of }A.\end{array}\nonumber\]

Los valores propios de\(v/C^{-1}v\) o\(v/Cv\) son los mismos.

Prueba

Supongamos que\(v\) es un vector propio de\(A\) con valor propio\(\lambda\), así que eso\(Av=\lambda v\). Entonces

\[B(C^{−1}v)=C^{−1}(CBC^{−1}v)=C^{−1}(Av)=C^{−1}\lambda v=\lambda (C^{−1}v),\nonumber\]

por lo que\(C^{−1}v\) es un vector propio de\(B\) con valor propio\(\lambda\). Así mismo si\(v\) es un vector propio de\(B\) con valor propio\(\lambda\), entonces\(Bv=\lambda v\), y tenemos

\[A(Cv)=(CBC^{−1})Cv=CBv=C(\lambda v)=\lambda (Cv),\nonumber\]

por lo que\(Cv\) es un valor propio de\(A\) con valor propio\(\lambda\).

Nota \(\PageIndex{6}\)

Si\(A=CBC^{−1}\), entonces\(C^{−1}\) toma el\(\lambda\) -espacio propio de\(A\) al\(\lambda\) -espacio propio de\(B\), y\(C\) toma el\(\lambda\) -espacio propio de\(B\) al\(\lambda\) -espacio propio de\(A\).

Ejemplo\(\PageIndex{9}\)

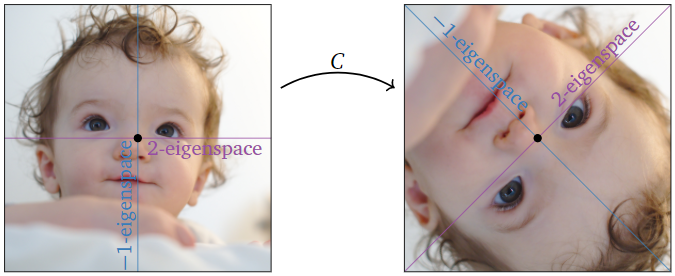
Seguimos con el ejemplo anterior\(\PageIndex{5}\): vamos

\[A=\left(\begin{array}{cc}1/2&3/2\\3/2&1/2\end{array}\right)\quad B=\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)\quad C=\left(\begin{array}{cc}1&1\\1&-1\end{array}\right),\nonumber\]

así\(A=CBC^{-1}\). Dejar\(v_1=\left(\begin{array}{c}1\\1\end{array}\right)\) y\(v_2=\left(\begin{array}{c}1\\-1\end{array}\right)\), las columnas de\(C\). Recordemos que:

• \(B\)escala la\(e_1\) -dirección por\(2\) y la\(e_2\) -dirección por\(-1\).
• \(A\)escala la\(v_1\) -dirección por\(2\) y la\(v_2\) -dirección por\(-1\).

Esto significa que el\(x\) -eje es el\(2\) -espacio propio de\(B\), y el\(y\) -eje es el\(−1\) -espacio propio de\(B\); asimismo, el “\(v_1\)-eje” es el\(2\) -espacio propio de\(A\), y el “\(v_2\)-eje” es el\(−1\) -espacio propio de\(A\). Esto es consistente con el hecho\(\PageIndex{3}\), como multiplicación por\(C\) cambios\(e_1\) en\(Ce_1=v_1\) y\(e_2\) en\(Ce_2=v_2\).

Figura\(\PageIndex{17}\)

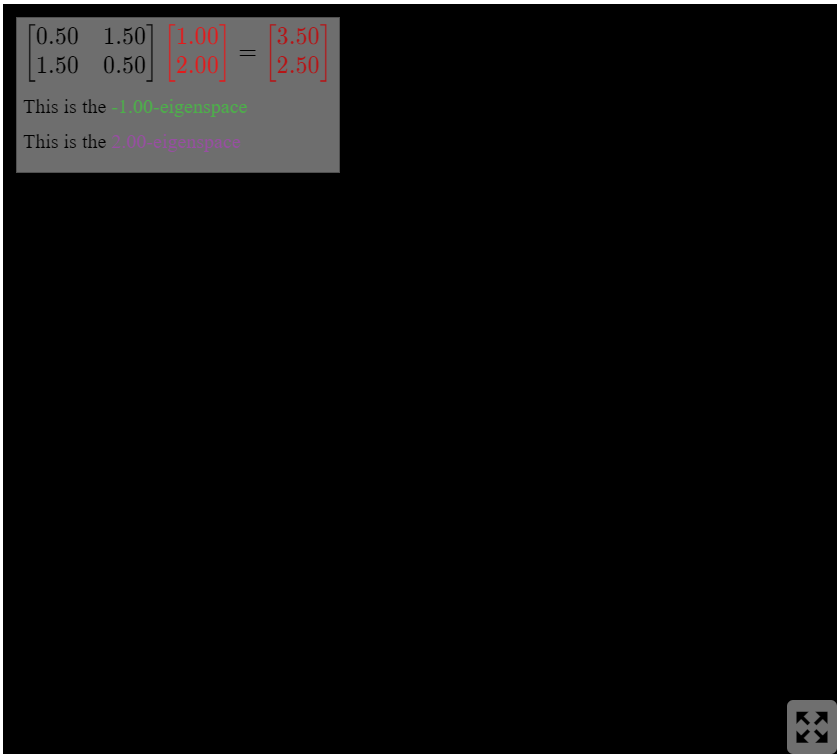
Figura\(\PageIndex{18}\): Los espacios propios de\(A\) son las líneas a través\(v_1\) y\(v_2\), Estas son las imágenes debajo\(C\) de los ejes de coordenadas, que son los espacios propios de\(B\).

Ejemplo\(\PageIndex{10}\): Interactive: Another matrix similar to \(B\)

Continuando con el Ejemplo\(\PageIndex{6}\), vamos

\[A'=\frac{1}{5}\left(\begin{array}{cc}-8&-9\\6&13\end{array}\right)\quad B=\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)\quad C'=\frac{1}{2}\left(\begin{array}{cc}-1&-3\\2&1\end{array}\right),\nonumber\]

así\(A'=C'B(C')^{−1}\). Dejar\(v_1'=\frac{1}{2}\left(\begin{array}{c}-1\\2\end{array}\right)\) y\(v_2'=\frac{1}{2}\left(\begin{array}{c}-3\\1\end{array}\right)\), las columnas de\(C'\). Entonces:

• \(B\)escala la\(e_1\) -dirección por\(2\) y la\(e_2\) -dirección por\(-1\).
• \(A'\)escala la\(v_1'\) -dirección por\(2\) y la\(v_2'\) -dirección por\(-1\).

Como antes, el\(x\) -eje es el\(2\) -espacio propio de\(B\), y el\(y\) -eje es el\(−1\) -espacio propio de\(B\); asimismo, el “\(v_1'\)-eje” es el\(2\) -espacio propio de\(A'\), y el “\(v_2'\)-eje” es el\(−1\) -espacio propio de\(A'\). Esto es consistente con el hecho\(\PageIndex{3}\), como multiplicación por\(C'\) cambios\(e_1\) en\(C'e_1=v_1'\) y\(e_2\) en\(C'e_2=v_2'\).

Figura\(\PageIndex{19}\)

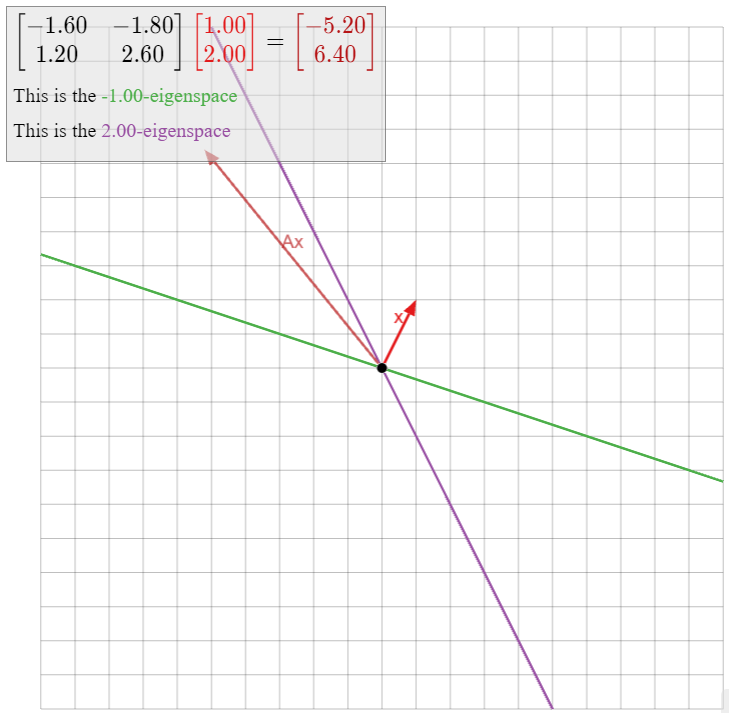
Figura\(\PageIndex{20}\): Los espacios propios de\(A'\) son las líneas a través\(v_1'\) y\(v_2'\). Estas son las imágenes debajo\(C'\) de los ejes de coordenadas, que son los espacios propios de\(B\).

Ejemplo\(\PageIndex{11}\): Interactive: Similar \(3\times 3\) matrices

Continuando con el Ejemplo\(\PageIndex{8}\), vamos

\[A=\left(\begin{array}{ccc}-1&0&0\\-1&0&2\\-1&1&1\end{array}\right)\quad B=\left(\begin{array}{ccc}-1&0&0\\0&-1&0\\0&0&2\end{array}\right)\quad C=\left(\begin{array}{ccc}-1&1&0\\1&1&1\\-1&0&1\end{array}\right),\nonumber\]

así\(A=CBC^{-1}\). Dejemos\(v_1\)\(v_2\),,\(v_3\) por las columnas de\(C\). Entonces:

• \(B\)escala el\(e_1\),\(e_2\) -plano por\(-1\) y la\(e_3\) -dirección por\(2\).
• \(A\)escala el\(v_1\),\(v_2\) -plano por\(-1\) y la\(v_3\) -dirección por\(2\).

En otras palabras, el\(xy\) -plano es el\(−1\) -espacio propio de\(B\), y el\(z\) -eje es el\(2\) -espacio propio de\(B\); asimismo, el “\(v_1\),\(v_2\) -plano” es el\(−1\) -espacio propio de\(A\), y el “\(v_3\)-eje” es el\(2\) -espacio propio de \(A\). Esto es consistente con el hecho\(\PageIndex{3}\), como multiplicación por\(C\) cambios\(e_1\)\(Ce_1=v_1,\: e_2\) en\(Ce_2=v_2\), y\(e_3\) en\(Ce_3=v_3\).

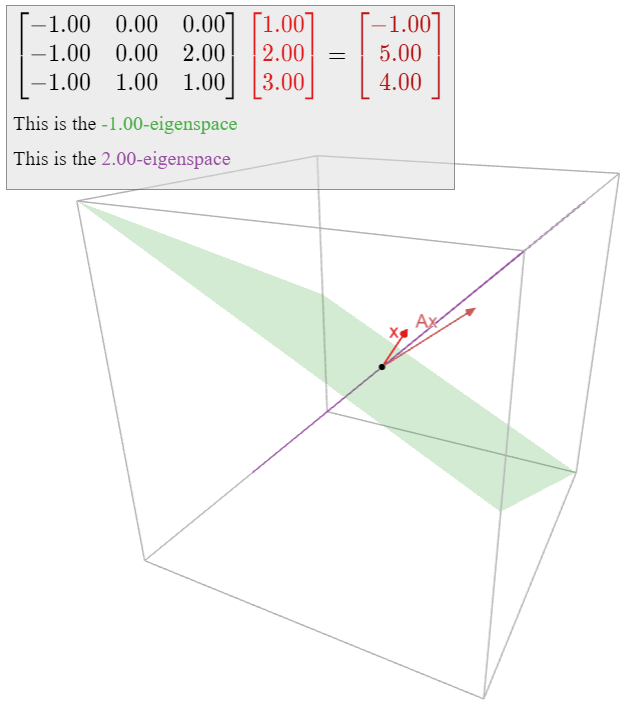
Figura\(\PageIndex{21}\): El\(−1\) -espacio propio de\(A\) es el plano verde, y el\(2\) -espacio propio de\(A\) es la línea violeta. Estas son las imágenes debajo\(C\) del\(xy\) -plano y el\(z\) -eje, respectivamente, que son los espacios propios de\(B\).