6: Ortogonalidad

Última actualización
Guardar como PDF

Page ID: 113073

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Recordemos por última vez la estructura de este libro:

Resolver la ecuación matricial$Ax=b$.
Resuelve la ecuación matricial$Ax=\lambda x\text{,}$ donde$\lambda$ está un número.
Resolver aproximadamente la ecuación matricial$Ax=b$.

Ahora hemos llegado a la tercera parte.

Nota$\PageIndex{1}$

Resolver aproximadamente la ecuación matricial$Ax=b.$

Encontrar soluciones aproximadas de ecuaciones generalmente requiere calcular el vector más cercano en un subespacio a un vector dado. Esto se convierte en un problema de ortogonalidad: se necesita saber qué vectores son perpendiculares al subespacio.

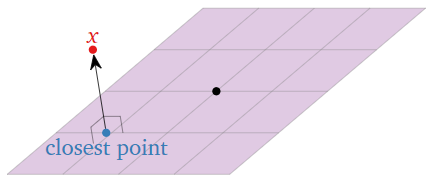
$clipboard_e4c312e06d8c1c7b40ae1ce8dfa3f77e5.png$

Figura$\PageIndex{1}$

Primero definiremos la ortogonalidad y aprenderemos a encontrar complementos ortogonales de subespacios en la Sección 6.1 y Sección 6.2. El núcleo de este capítulo es la Sección 6.3, en la que se discute la proyección ortogonal de un vector sobre un subespacio; este es un método para calcular el vector más cercano en un subespacio a un vector dado. Estos cálculos se vuelven más fáciles ante la presencia de un conjunto ortogonal, como veremos en la Sección 6.4. En la Sección 6.5 presentaremos el método de mínimos cuadrados para resolver aproximadamente sistemas de ecuaciones, y daremos aplicaciones al modelado de datos.

Ejemplo$\PageIndex{1}$

En el modelado de datos, a menudo se pregunta: “¿en qué línea se supone que mienten mis datos?” Esto se puede resolver usando una simple aplicación del método de mínimos cuadrados.

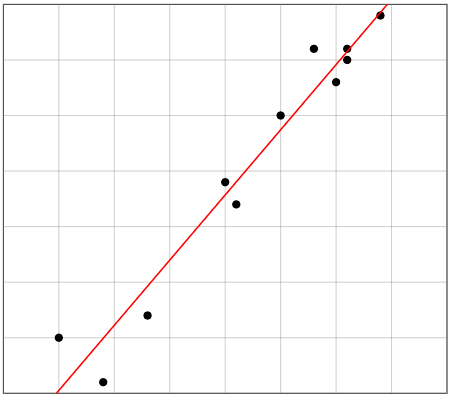
$clipboard_e9c04a2611d7045928bccedd7ad9c0a17.png$

Figura$\PageIndex{2}$

Ejemplo$\PageIndex{2}$

Gauss inventó el método de mínimos cuadrados para encontrar una elipse que mejor se ajuste: predijo correctamente la órbita (elíptica) del asteroide Ceres al pasar detrás del sol en 1801.

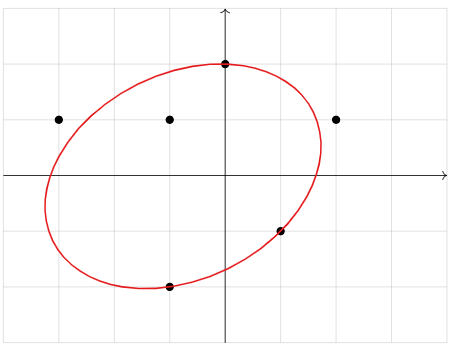
$clipboard_e8ec747dcd6cf56fd41cfcac28daede0f.png$

Figura$\PageIndex{3}$

6.1: Productos punteados y ortogonalidad
En este capítulo, será necesario encontrar el punto más cercano en un subespacio a un punto dado. El punto más cercano tiene la propiedad de que la diferencia entre los dos puntos es ortogonal, o perpendicular, al subespacio. Por esta razón, necesitamos desarrollar nociones de ortogonalidad, longitud y distancia.
6.2: Complementos ortogonales
Será importante calcular el conjunto de todos los vectores que son ortogonales a un conjunto dado de vectores. Resulta que un vector es ortogonal a un conjunto de vectores si y sólo si es ortogonal al lapso de esos vectores, que es un subespacio, por lo que nos limitamos al caso de los subespacios.
6.3: Proyección ortogonal
Sea W un subespacio de Rn y deje que x sea un vector en Rn. En esta sección, aprenderemos a calcular el vector xW más cercano a x en W. El vector xW se denomina proyección ortogonal de x sobre W. Esto es exactamente lo que usaremos para resolver casi ecuaciones matriciales.
6.4: Conjuntos ortogonales
6.5: El Método de los Mínimos Cuadrados

Search

Text Color

Text Size

Margin Size

Font Type

Nota\(\PageIndex{1}\)

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)