5.6: Matrices Estocásticas
- Page ID
- 113118
- Aprende ejemplos de matrices estocásticas y aplicaciones a ecuaciones de diferencia.
- Entender el algoritmo PageRank de Google.
- Receta: encontrar el estado estacionario de una matriz estocástica positiva.
- Cuadro: dinámica de una matriz estocástica positiva.
- Teorema: el teorema de Perron-Frobenius.
- Palabras de vocabulario: ecuación de diferencia, matriz estocástica (positiva), estado estacionario, matriz de importancia, matriz de Google.
Esta sección está dedicada a un tipo común de aplicación de los valores propios: al estudio de ecuaciones de diferencia, en particular a las cadenas de Markov. Introduciremos matrices estocásticas, que codifican este tipo de ecuaciones de diferencia, y cubriremos en detalle el ejemplo más famoso de una matriz estocástica: la Matriz de Google.
Ecuaciones de diferencia
Supongamos que estamos estudiando un sistema cuyo estado en un momento dado puede ser descrito por una lista de números: por ejemplo, el número de conejos de edad\(0,1,\) y\(2\) años, respectivamente, o el número de copias de Pronóstico Negativo en cada uno de los quioscos de Caja Roja en Atlanta. En cada caso, podemos representar el estado en el momento\(t\) mediante un vector\(v_t\). Suponemos que\(t\) representa una cantidad de tiempo discreta: es decir,\(v_t\) es el estado “el día\(t\)” o “al año\(t\)”. Supongamos además que el estado en el momento\(t+1\) está relacionado con el estado\(t\) en el tiempo de manera lineal:\(v_{t+1}=Av_t\) para alguna matriz\(A\). Esta es la situación que consideraremos en esta subsección.
Una ecuación de diferencia es una ecuación de la forma
\[ v_{t+1} = Av_t \nonumber \]
para una\(n\times n\) matriz\(A\) y vectores\(v_0,v_1,v_2,\ldots\) en\(\mathbb{R}^n \).
En otras palabras:
- \(v_t\)es el “estado en el momento\(t\text{,}\)”
- \(v_{t+1}\)es el “estado en el momento\(t+1\text{,}\)” y
- \(v_{t+1}=Av_t\)significa que\(A\) es la “matriz de cambio de estado”.
Tenga en cuenta que
\[ v_t = Av_{t-1} = A^2v_{t-2} = \cdots = A^tv_0, \nonumber \]
lo que debería indicarle que el comportamiento a largo plazo de una ecuación de diferencia es un problema de valor propio.
Utilizaremos el siguiente ejemplo en esta subsección y en la siguiente. Entender esta sección equivale a entender este ejemplo.
Red Box tiene quioscos por todo Atlanta donde puedes rentar películas. Puedes devolverlos a cualquier otro quiosco. Por simplicidad, finge que hay tres quioscos en Atlanta, y que cada cliente devuelva su película al día siguiente. Dejar\(v_t\) ser el vector cuyas entradas\(x_t,y_t,z_t\) son el número de copias de Pronóstico Negativo en los quioscos\(1,2,\) y\(3\text{,}\) respectivamente. \(A\)Sea la matriz cuya\(i,j\) -entrada es la probabilidad de que un cliente que alquila Pronóstico Negativo del quiosco lo\(j\) devuelva al quiosco\(i\). Por ejemplo, la matriz
\[ A = \left(\begin{array}{ccc}.3&.4&.5 \\ .3&.4&\color{Red}{.3} \\ \color{Green}{.4}&\color{black}{.2}&\color{black}{.2}\end{array}\right) \nonumber \]
codifica una\(\color{Red}30\%\) probabilidad de que un cliente que alquila desde el quiosco 3 devuelva la película al quiosco 2, y una\(\color{Green}40\%\) probabilidad de que una película alquilada del quiosco\(1\) sea devuelta al quiosco\(3\). La segunda fila (por ejemplo) de la matriz\(A\) dice:
El número de películas regresadas al quiosco\(2\) será (en promedio):
\[ \begin{split} 30\% \amp\text{ of the movies from kiosk } 1 \\ 40\% \amp\text{ of the movies from kiosk } 2 \\ 30\% \amp\text{ of the movies from kiosk } 3 \\ \end{split} \nonumber \]
Aplicando esto a las tres filas, esto significa
\[ A\left(\begin{array}{c}x_t \\ y_t \\ z_t\end{array}\right) = \left(\begin{array}{c}.3x_t+.4y_t+.5z_t \\ .3x_t+.4y_t+.3z_t \\ .4x_t+.2y_t+.2z_t\end{array}\right). \nonumber \]
Por lo tanto,\(Av_t\) representa el número de películas en cada quiosco al día siguiente:
\[ Av_t = v_{t+1}. \nonumber \]
Este sistema está modelado por una ecuación de diferencia.
Una pregunta importante para hacer sobre una ecuación de diferencia es: ¿cuál es su comportamiento a largo plazo? ¿Cuántas películas habrá en cada quiosco después de 100 días? En la siguiente subsección, vamos a responder a esta pregunta para un tipo particular de ecuación de diferencia.
En una población de conejos,
- la mitad de los conejos recién nacidos sobreviven a su primer año;
- de ellos, la mitad sobrevive a su segundo año;
- la vida útil máxima es de tres años;
- los conejos producen\(0\)\(6\),\(8\) conejos en su primer, segundo y tercer año, respectivamente.
Dejar\(v_t\) ser el vector cuyas entradas\(x_t,y_t,z_t\) son el número de conejos envejecidos\(0, 1\text{,}\) y\(2\text{,}\) respectivamente. Las reglas anteriores se pueden escribir como un sistema de ecuaciones:
\[\begin{array}{rrrrrrr}x_{t+1} &=& {}&{}&6y_t &+& 8z_t\\ y_{t+1} &=& \frac 12x_t&{}&{}&{}&{} \\ z_{t+1} &=& {}&{}& \frac 12y_t.&{}&{}\end{array}\nonumber\]
En forma de matriz, esto dice:
\[ \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right) v_t = v_{t+1}. \nonumber \]
Este sistema está modelado por una ecuación de diferencia.
Definir
\[ A = \left(\begin{array}{ccc}0&6&8\\ \frac{1}{2}&0&0\\0&\frac{1}{2}&0\end{array}\right). \nonumber \]
Calculamos\(A\) tiene valores propios\(2\) y\(-1\text{,}\) y que un vector propio con valor propio\(2\) es
\[ v = \left(\begin{array}{c}16\\4\\1\end{array}\right). \nonumber \]
Esto explica parcialmente por qué\(x_t:y_t:z_t\) se acerca la relación\(16:4:1\) y por qué las tres cantidades eventualmente se duplican cada año en esta demostración:
Matrices estocásticas y el estado estacionario
En esta subsección, discutimos ecuaciones de diferencia que representan probabilidades, como el ejemplo de la Caja Roja\(\PageIndex{1}\). Tales sistemas se llaman cadenas de Markov. El resultado más importante en esta sección es el teorema de Perron-Frobenius, que describe el comportamiento a largo plazo de una cadena de Markov.
Una matriz cuadrada\(A\) es estocástica si todas sus entradas son no negativas, y las entradas de cada columna suman a\(1\).
Una matriz es positiva si todas sus entradas son números positivos.
Una matriz estocástica positiva es una matriz estocástica cuyas entradas son todas números positivos. En particular, ninguna entrada es igual a cero. Por ejemplo, la primera matriz a continuación es una matriz estocástica positiva, y la segunda no es:
\[\left(\begin{array}{ccc}.3&.4&.5\\.3&.4&.3\\.4&.2&.2\end{array}\right) \qquad \left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right). \nonumber \]
De manera más general, una matriz estocástica regular es una matriz estocástica\(A\) tal que\(A^n\) es positiva para algunos\(n \geq 1\). El teorema de Perron-Frobenius a continuación también se aplica a las matrices estocásticas regulares.
Continuando con el ejemplo de Caja Roja\(\PageIndex{1}\), la matriz
\[ A = \left(\begin{array}{ccc}.3&.4&.5\\.3&.4&.3\\.4&.2&.2\end{array}\right) \nonumber \]
es una matriz estocástica positiva. El hecho de que las columnas sumen a\(1\) dice que todas las películas rentadas de un quiosco en particular deben ser devueltas a algún otro quiosco (recuerde que cada cliente devuelve su película al día siguiente). Por ejemplo, la primera columna dice:
De las películas rentadas de kiosco\(1\text{,}\)
\[ \begin{split} 30\% \amp\text{ will be returned to kiosk } 1 \\ 30\% \amp\text{ will be returned to kiosk } 2 \\ 40\% \amp\text{ will be returned to kiosk } 3. \\ \end{split} \nonumber \]
La suma es\(100\%\text{,}\) como todas las películas son devueltas a uno de los tres quioscos.
La matriz\(A\) representa el cambio de estado de un día a otro:
\[ \left(\begin{array}{c}x_{t+1}\\y_{t+1}\\z_{t+1}\end{array}\right) = A\left(\begin{array}{c}x_t\\y_t\\z_t\end{array}\right) =\left(\begin{array}{c}.3x_t+.4y_t+.5z_t \\ .3x_t+.4y_t+.3z_t \\ .4x_t+.2y_t+.2z_t\end{array}\right). \nonumber \]
Si sumamos las entradas de\(v_{t+1}\text{,}\) obtenemos
\[ \begin{split} \amp(.3x_t+.4y_t+.5z_t)+ (.3x_t+.4y_t+.3z_t)+ (.4x_t+.2y_t+.2z_t) \\ \amp\qquad=(.3+.3+.4)x_t + (.4+.4+.2)y_t + (.5+.3+.2)z_t \\ \amp\qquad= x_t + y_t + z_t. \end{split} \nonumber \]
Esto dice que el número total de copias de Pronóstico Negativo en los tres quioscos no cambia día a día, como esperamos.
El hecho de que las entradas de los vectores\(v_t\) y\(v_{t+1}\) sumen al mismo número es consecuencia del hecho de que las columnas de una matriz estocástica suman a\(1\).
Dejar\(A\) ser una matriz estocástica, dejar\(v_t\) ser un vector, y dejar\(v_{t+1} = Av_t\). Entonces la suma de las entradas de\(v_t\) es igual a la suma de las entradas de\(v_{t+1}\).
El cálculo del comportamiento a largo plazo de una ecuación de diferencia resulta ser un problema de valor propio. Los valores propios de las matrices estocásticas tienen propiedades muy especiales.
Dejar\(A\) ser una matriz estocástica. Entonces:
- \(1\)es un valor propio de\(A.\)
- Si\(\lambda\) es un valor propio (real o complejo) de\(A\text{,}\) entonces\(|\lambda|\leq 1.\)
- Prueba
-
Si\(A\) es estocástico, entonces las filas de\(A^T\) suma a\(1\). Pero multiplicar una matriz por el vector\((1,1,\ldots,1)\) suma las filas:
\[\left(\begin{array}{ccc}.3&.3&.4\\.4&.4&.2\\.5&.3&.2\end{array}\right)\left(\begin{array}{c}1\\1\\1\end{array}\right)=\left(\begin{array}{c}.3+.3+.4\\.4+.4+.2\\.5+.3+.2\end{array}\right)=\left(\begin{array}{c}1\\1\\1\end{array}\right).\nonumber\]
Por lo tanto,\(1\) es un valor propio de\(A^T\). Pero\(A\) y\(A^T\) tienen el mismo polinomio característico:
\[ \det(A-\lambda I_n) = \det\bigl((A-\lambda I_n)^T\bigr) = \det(A^T - \lambda I_n). \nonumber \]
Por lo tanto,\(1\) es un valor propio de\(A\).
Ahora vamos a\(\lambda\) ser cualquier valor propio de\(A\text{,}\) por lo que también es un valor propio de\(A^T\). Dejar\(x = (x_1,x_2,\ldots,x_n)\) ser un vector propio de\(A^T\) con valor propio\(\lambda\text{,}\) así\(\lambda x = A^Tx\). La entrada\(j\) th de esta ecuación vectorial es
\[ \lambda x_j = \sum_{i=1}^n a_{ij} x_i. \nonumber \]
Elige\(x_j\) con el mayor valor absoluto, así que\(|x_i|\leq|x_j|\) para todos\(i\). Entonces
\[ |\lambda|\cdot|x_j| = \left\vert \sum_{i=1}^n a_{ij} x_i \right\vert \leq \sum_{i=1}^n a_{ij}\cdot |x_i| \leq \sum_{i=1}^n a_{ij}\cdot |x_j| = 1\cdot|x_j|, \nonumber \]
donde se sostiene la última igualdad porque\(\sum_{i=1}^n a_{ij}=1\). Esto implica\(|\lambda|\leq 1.\)
De hecho, para\(A\text{,}\) una matriz estocástica positiva se puede demostrar que si\(\lambda\neq 1\) es un valor propio (real o complejo) de\(A\text{,}\) entonces\(|\lambda|\lt 1.\) El\(1\) -espacio propio de una matriz estocástica es muy importante.
Un estado estacionario de una matriz estocástica\(A\) es un vector propio\(w\) con valor propio\(1\text{,}\) tal que las entradas son positivas y se suman a\(1\).
El teorema de Perron-Frobenius describe el comportamiento a largo plazo de una ecuación de diferencia representada por una matriz estocástica. Su prueba está fuera del alcance de este texto.
Dejar\(A\) ser una matriz estocástica positiva. Luego\(A\) admite un vector de estado estacionario único\(w\text{,}\) que abarca el\(1\) espacio propio.
Además, para cualquier vector\(v_0\) con entradas sumando a algún número,\(c\text{,}\) las iteraciones
\[ v_1 = Av_0,\; v_2 = Av_1,\; \ldots,\; v_t = Av_{t-1},\; \ldots \nonumber \]
acercarse a\(cw\) medida que\(t\) se hace grande.
Traducción: El teorema de Perrón-Frobenius hace las siguientes afirmaciones:
- El\(1\) -espacio propio de una matriz estocástica positiva es una línea.
- El espacio\(1\) -eigenspace contiene un vector con entradas positivas.
- Todos los vectores se acercan al\(1\) espacio propio tras la multiplicación repetida por\(A\).
Uno debería pensar en un vector de estado estacionario\(w\) como un vector de porcentajes. Por ejemplo, si las películas se distribuyen de acuerdo a estos porcentajes hoy, entonces van a tener la misma distribución mañana, ya que\(Aw=w\). Y no importa la distribución inicial de películas, la distribución a largo plazo siempre será el vector de estado estacionario.
La suma\(c\) de las entradas de\(v_0\) es el número total de cosas en el sistema que se modela. El número total no cambia, por lo que el estado a largo plazo del sistema debe acercarse a\(cw\text{:}\) él es un múltiplo de\(w\) porque está contenido en\(1\) el -espacio propio, y las entradas de\(cw\) sum to\(c\).
Dejar\(A\) ser una matriz estocástica positiva. Aquí se explica cómo calcular el vector de estado estacionario de\(A.\)
- Encuentra cualquier vector propio\(v\) de\(A\) con valor propio\(1\) resolviendo\((A-I_n)v = 0\).
- Dividir\(v\) por la suma de las entradas de\(v\) para obtener un vector\(w\) cuyas entradas sumen a\(1.\)
- Este vector automáticamente tiene entradas positivas. Es el vector único de estado estacionario.
La receta anterior es adecuada para cálculos a mano, pero no aprovecha el hecho de que\(A\) es una matriz estocástica. En la práctica, generalmente es más rápido calcular un vector de estado estacionario por computadora de la siguiente manera:
Dejar\(A\) ser una matriz estocástica positiva. Aquí se explica cómo aproximar el vector de estado estacionario de\(A\) con una computadora.
- Elija cualquier vector\(v_0\) cuyas entradas sumen a\(1\) (por ejemplo, un vector de coordenadas estándar).
- Calcular\(v_1 = Av_0,\,v_2 = Av_1,\,v_3=Av_2,\,\) etc.
- Estos convergen al vector de estado estacionario\(w\).
Considerar la matriz estocástica positiva
\[ A = \left(\begin{array}{cc}3/4&1/4 \\ 1/4&3/4\end{array}\right). \nonumber \]
Esta matriz tiene polinomio característico
\[ f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(\lambda) = \lambda^2 - \frac32\lambda + \frac12 = (\lambda - 1)(\lambda-1/2). \nonumber \]
Observe que\(1\) es estrictamente mayor que el otro valor propio, y que tiene multiplicidad algebraica (por lo tanto, geométrica)\(1\). Calculamos vectores propios para que los valores propios\(1,1/2\) sean, respectivamente,
\[ u_1 = \left(\begin{array}{c}1\\1\end{array}\right) \qquad u_2 = \left(\begin{array}{c}1\\-1\end{array}\right). \nonumber \]
El vector propio tiene\(u_1\) necesariamente entradas positivas; el vector de estado estacionario es
\[ w = \frac 1{1+1}\left(\begin{array}{c}1\\1\end{array}\right) = \frac 12\left(\begin{array}{c}1\\1\end{array}\right) = \left(\begin{array}{c}50\% \\ 50\%\end{array}\right). \nonumber \]
El teorema de Perron-Frobenius afirma que, para cualquier vector\(v_0\text{,}\) los vectores se\(v_1 = Av_0,\,v_2=Av_1,\,\ldots\) acercan a un vector cuyas entradas son las mismas:\(50\%\) de la suma estará en la primera entrada, y\(50\%\) estará en la segunda.
Esto lo podemos ver explícitamente, de la siguiente manera. Los vectores propios\(u_1,u_2\) forman una base\(\mathcal{B}\)\(\mathbb{R}^2 \text{;}\) para cualquier vector\(x = a_1u_1 + a_2u_2\) en\(\mathbb{R}^2 \text{,}\) que tenemos
\[ Ax = A(a_1u_1+a_2u_2) = a_1Au_1 + a_2Au_2 = a_1u_1 + \frac{a_2}2u_2. \nonumber \]
Iterando la multiplicación\(A\) de esta manera, tenemos
\[ A^tx = a_1u_1 + \frac{a_2}{2^t}u_2 \;\to \; a_1u_1 \nonumber \]
como\(t\to\infty\). Esto demuestra que se\(A^tx\) acerca
\[ a_1u_1 = \left(\begin{array}{c}a_1 \\ a_1\end{array}\right). \nonumber \]
Obsérvese que la suma de las entradas de\(a_1u_1\) es igual a la suma de las entradas de\(a_1u_1+a_2u_2\text{,}\) desde las entradas de\(u_2\) suma a\(0\).
Para ilustrar el teorema con números, escojamos un valor particular para\(u_0\text{,}\) decir\(u_0={1\choose 0}\). Calculamos los valores para\(u_t = {x_t\choose y_t}\) en esta tabla:
\[ \begin{array}{c|c|c|c} t & x_t & y_t \\\hline 0 & 1.000 & 0.000 \\ 1 & 0.750 & 0.250 \\ 2 & 0.625 & 0.375 \\ 3 & 0.563 & 0.438 \\ 4 & 0.531 & 0.469 \\ 5 & 0.516 & 0.484 \\ 6 & 0.508 & 0.492 \\ 7 & 0.504 & 0.496 \\ 8 & 0.502 & 0.498 \\ 9 & 0.501 & 0.499 \\ 10& 0.500 & 0.500 \\ \end{array} \nonumber \]
Vemos que\(u_t\) efectivamente se aproxima\({0.5\choose0.5}\).
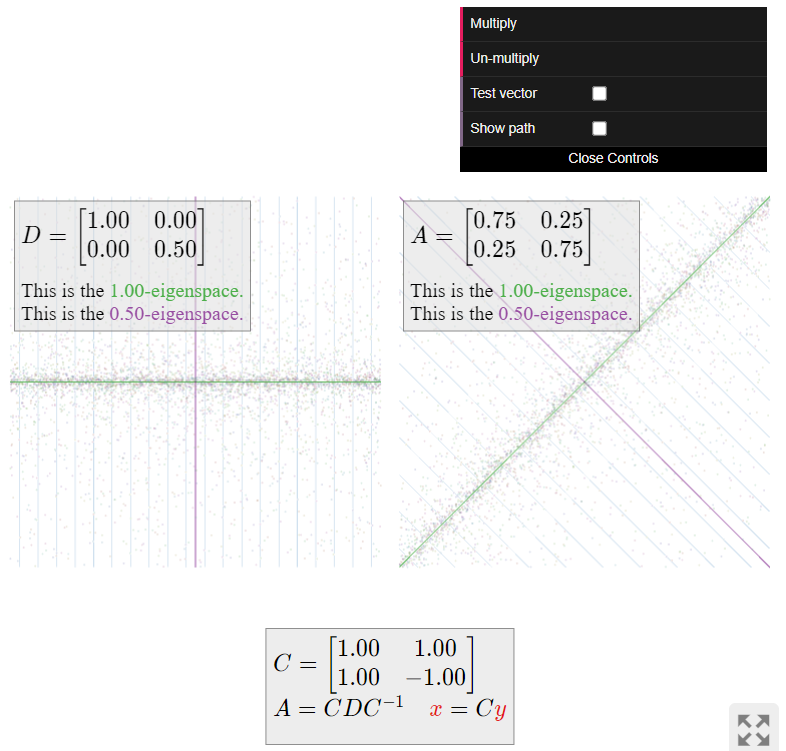
Ahora pasamos a visualizar la dinámica de (es decir, multiplicación repetida por) la matriz\(A\). Esta matriz es diagonalizable; tenemos\(A=CDC^{-1}\) para
\[ C = \left(\begin{array}{cc}1&1\\1&-1\end{array}\right) \qquad D = \left(\begin{array}{cc}1&0\\0&1/2\end{array}\right). \nonumber \]
La matriz\(D\) deja la\(x\) coordenada -sin cambios y escala la\(y\) coordenada -por\(1/2\). La multiplicación repetida por\(D\) hace que la\(y\) coordenada -sea muy pequeña, por lo que “chupa todos los vectores en el\(x\) eje -”.
La matriz\(A\) hace lo mismo que\(D\text{,}\) pero con respecto al sistema de coordenadas definido por las columnas\(u_1,u_2\) de\(C\). Esto quiere decir que\(A\) “chupa todos los vectores en el\(1\) -espacio propio”, sin cambiar la suma de las entradas de los vectores.
Continuando con el ejemplo de Caja Roja\(\PageIndex{1}\), podemos ilustrar explícitamente el teorema de Perron-Frobenius. La matriz
\[ A = \left(\begin{array}{ccc}.3&.4&.5\\.3&.4&.3\\.4&.2&.2\end{array}\right) \nonumber \]
tiene polinomio característico
\[ f(\lambda) = -\lambda^3 + 0.12\lambda - 0.02 = -(\lambda-1)(\lambda+0.2)(\lambda-0.1). \nonumber \]
Observe que\(1\) es estrictamente mayor en valor absoluto que los otros valores propios, y que tiene multiplicidad algebraica (por lo tanto, geométrica)\(1\). Calculamos vectores propios para que los valores propios\(1,-0.2,0.1\) sean, respectivamente,
\[ u_1 = \left(\begin{array}{c}7\\6\\5\end{array}\right) \qquad u_2 = \left(\begin{array}{c}-1\\0\\1\end{array}\right) \qquad u_3 = \left(\begin{array}{c}1\\-3\\2\end{array}\right). \nonumber \]
El vector propio tiene\(u_1\) necesariamente entradas positivas; el vector de estado estacionario es
\[ w = \frac 1{7+6+5}u_1 = \frac 1{18}\left(\begin{array}{c}7\\6\\5\end{array}\right). \nonumber \]
Los vectores propios\(u_1,u_2,u_3\) forman una base\(\mathcal{B}\)\(\mathbb{R}^3 \text{;}\) para cualquier vector\(x = a_1u_1+a_2u_2+a_3u_3\) en\(\mathbb{R}^3 \text{,}\) que tenemos
\[ \begin{split} Ax \amp= A(a_1u_1+a_2u_2+a_3u_3) \\ \amp= a_1Au_1 + a_2Au_2 + a_3Au_3 \\ \amp= a_1u_1 - 0.2a_2u_2 + 0.1a_3u_3. \end{split} \nonumber \]
Iterando la multiplicación\(A\) de esta manera, tenemos
\[ A^tx = a_1u_1 - (0.2)^ta_2u_2 + (0.1)^ta_3u_3 \;\to \; a_1u_1 \nonumber \]
como\(t\to\infty\). Esto demuestra que se\(A^tx\) aproxima\(a_1u_1\text{,}\) que es un vector propio con valor propio\(1\), como lo garantiza el teorema de Perron-Frobenius.
¿Qué dicen los cálculos anteriores sobre el número de copias de Pronóstico Negativo en los quioscos de Atlanta Red Box? Supongamos que los quioscos inician con 100 copias de la película, con\(30\) copias en el quiosco 1,\(50\) copias en quiosco\(2\text{,}\) y\(20\) copias en quiosco\(3\). Dejado\(v_0 = (30,50,20)\) ser el vector que describe este estado. Después habrá\(v_1 = Av_0\) películas en los quioscos al día siguiente,\(v_2 = Av_1\) al día siguiente, y así sucesivamente. Dejamos\(v_t = (x_t,y_t,z_t).\)
\[ \begin{array}{c|c|c|c} t & x_t & y_t & z_t \\\hline 0 & 30.000000 & 50.000000 & 20.000000 \\ 1 & 39.000000 & 35.000000 & 26.000000 \\ 2 & 38.700000 & 33.500000 & 27.800000 \\ 3 & 38.910000 & 33.350000 & 27.740000 \\ 4 & 38.883000 & 33.335000 & 27.782000 \\ 5 & 38.889900 & 33.333500 & 27.776600 \\ 6 & 38.888670 & 33.333350 & 27.777980 \\ 7 & 38.888931 & 33.333335 & 27.777734 \\ 8 & 38.888880 & 33.333333 & 27.777786 \\ 9 & 38.888891 & 33.333333 & 27.777776 \\ 10& 38.888889 & 33.333333 & 27.777778 \\ \end{array} \nonumber \]
(Por supuesto que no tiene sentido tener un número fraccional de películas; aquí se incluyen los decimales para ilustrar la convergencia). El vector de estado estacionario dice que eventualmente, las películas se distribuirán en los quioscos de acuerdo a los porcentajes
\[ w = \frac 1{18}\left(\begin{array}{c}7\\6\\5\end{array}\right) = \left(\begin{array}{c}38.888888\% \\ 33.333333\% \\ 27.777778\%\end{array}\right), \nonumber \]
que concuerda con el cuadro anterior. Además, esta distribución es independiente de la distribución inicial de películas en los quioscos.
Ahora pasamos a visualizar la dinámica de (es decir, multiplicación repetida por) la matriz\(A\). Esta matriz es diagonalizable; tenemos\(A=CDC^{-1}\) para
\[ C = \left(\begin{array}{ccc}7&-1&1\\6&0&-3\\5&1&2\end{array}\right) \qquad D = \left(\begin{array}{ccc}1&0&0\\0&-.2&0\\0&0&.1\end{array}\right). \nonumber \]
La matriz\(D\) deja la\(x\) coordenada -sin cambios, escala la\(y\) coordenada por\(-1/5\text{,}\) y escala la\(z\) coordenada -por\(1/10\). La multiplicación repetida por\(D\) hace que las\(z\) coordenadas\(y\) - y -sean muy pequeñas, por lo que “chupa todos los vectores en el\(x\) eje -”.
La matriz\(A\) hace lo mismo que\(D\text{,}\) pero con respecto al sistema de coordenadas definido por las columnas\(u_1,u_2,u_3\) de\(C\). Esto quiere decir que\(A\) “chupa todos los vectores en el\(1\) -espacio propio”, sin cambiar la suma de las entradas de los vectores.
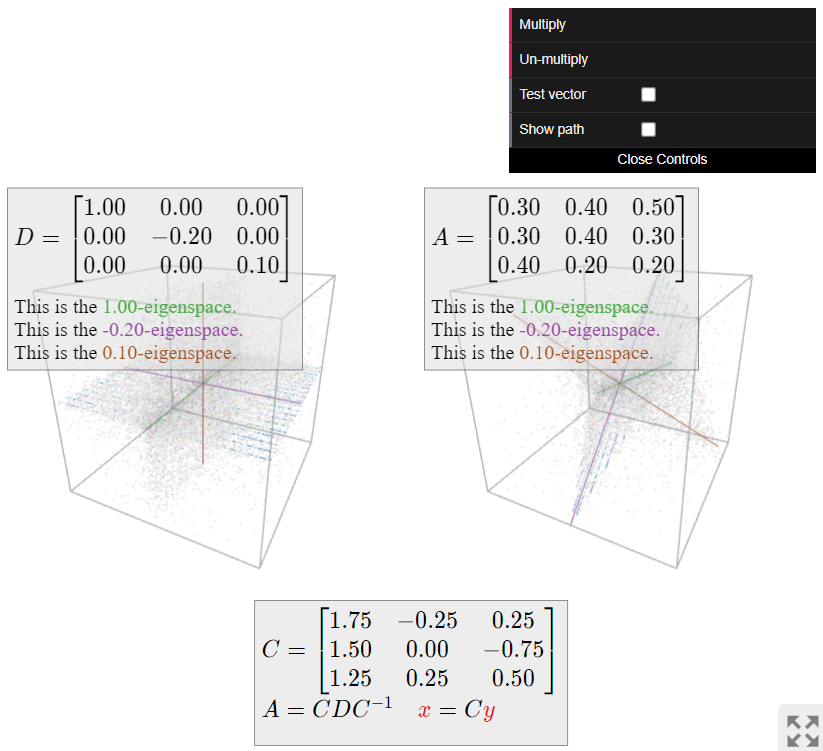
La imagen de una matriz estocástica positiva es siempre la misma, sea o no diagonalizable: todos los vectores son “aspirados al\(1\) -espacio propio”, que es una línea, sin cambiar la suma de las entradas de los vectores. Este es el contenido geométrico del teorema de Perron-Frobenius.
El algoritmo PageRank de Google
La búsqueda en Internet en la década de 1990 fue muy ineficiente. Yahoo o AltaVista escanearían páginas para su texto de búsqueda, y simplemente enumerarían los resultados con la mayor cantidad de ocurrencias de esas palabras. No es sorprendente que los sitios web más picantes pronto aprendieran que al poner las palabras “Alanis Morissette” un millón de veces en sus páginas, podían aparecer primero cada vez que un adolescente angsty intentaba encontrar Jagged Little Pill en Napster.
Larry Page y Sergey Brin inventaron una manera de clasificar las páginas por importancia. Fundaron Google en base a su algoritmo. Aquí es más o menos cómo funciona.
Cada página web tiene una importancia asociada, o rango. Este es un número positivo. Este rango está determinado por la siguiente regla.
Si una página\(P\) enlaza con\(n\) otras páginas\(Q_1,Q_2,\ldots,Q_n\text{,}\), entonces cada página\(Q_i\) hereda\(\frac 1n\)\(P\) de su importancia.
En la práctica, esto significa:
- Si una página muy importante enlaza a tu página (y no a un trillón de otras también), entonces tu página se considera importante.
- Si un trillón de páginas sin importancia enlazan a su página, entonces su página sigue siendo importante.
- Si solo una página desconocida enlaza con la tuya, tu página no es importante.
Alternativamente, está la interpretación del surfista aleatorio. Un “surfista aleatorio” simplemente se sienta frente a su computadora todo el día, haciendo clic aleatoriamente en los enlaces. Las páginas en las que pasa más tiempo deberían ser las más importantes. Entonces, las páginas importantes (de alto rango) son aquellas en las que un surfista aleatorio terminará con mayor frecuencia. Esta medida resulta ser equivalente al rango.
Considera un internet con\(n\) páginas. La matriz de importancia es la\(n\times n\) matriz\(A\) cuya\(i,j\) entrada es la importancia que la página\(j\) pasa a la página\(i.\)
Observe que la matriz de importancia es una matriz estocástica, asumiendo que cada página contiene un enlace: si la página\(i\) tiene\(m\) enlaces, entonces la columna\(i\) th contiene el número\(1/m\text{,}\)\(m\) veces, y el número cero en las otras entradas.
Considera el siguiente internet con sólo cuatro páginas. Los enlaces están indicados por flechas.
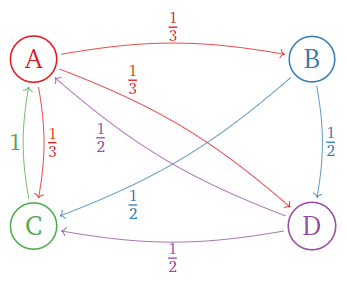
Figura\(\PageIndex{4}\)
La regla de importancia dice:
- \(\color{Red}A\)La página tiene\(3\) enlaces, por lo que pasa\(\frac 13\) de su importancia a las páginas\(B,C,D\).
- \(\color{blue}B\)La página tiene\(2\) enlaces, por lo que pasa\(\frac 12\) de su importancia a las páginas\(C,D\).
- \(\color{Green}C\)La página tiene un enlace, por lo que pasa toda su importancia a la página\(A\).
- \(\color{Purple}D\)La página tiene\(2\) enlaces, por lo que pasa\(\frac 12\) de su importancia a las páginas\(A,C\).
En términos de matrices, si\(v = (a,b,c,d)\) es el vector que contiene los rangos\(a,b,c,d\) de las páginas\(A,B,C,D\text{,}\) entonces
\[\left(\begin{array}{cccc}\color{Red}{0}&\color{blue}{0}&\color{Green}{1}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{0}&\color{Green}{0}&\color{Purple}{0} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{0}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{0}&\color{Purple}{0}\end{array}\right)\left(\begin{array}{c}a\\b\\c\\d\end{array}\right)=\left(\begin{array}{lr}{}&{c+\frac{1}{2}d} \\ {\frac{1}{3}a}&{}\\ {\frac{1}{3}a+\frac{1}{2}b}&{+\frac{1}{2}d} \\ {\frac{1}{3}a+\frac{1}{2}b}&{}\end{array}\right)=\left(\begin{array}{c}a\\b\\c\\d\end{array}\right).\nonumber\]
La matriz de la izquierda es la matriz de importancia, y la igualdad final expresa la regla de importancia.
El ejemplo anterior ilustra la observación clave.
El vector rank es un vector propio de la matriz de importancia con valor propio\(1\).
A la luz de la observación clave, nos gustaría usar el teorema de Perron-Frobenius para encontrar el vector de rango. Desafortunadamente, la matriz de importancia no siempre es una matriz estocástica positiva.
Considera el siguiente internet con tres páginas:
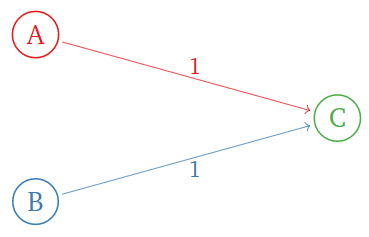
Figura\(\PageIndex{5}\)
La matriz de importancia es
\[\left(\begin{array}{ccc}\color{Red}{0}&\color{blue}{0}&\color{Green}{0} \\ \color{Red}{0}&\color{blue}{0}&\color{Green}{0} \\ \color{Red}{1}&\color{blue}{1}&\color{Green}{0}\end{array}\right).\nonumber\]
Esto tiene polinomio característico
\[ f(\lambda) = \det\left(\begin{array}{ccc}-\lambda&0&0\\ 0&-\lambda&0 \\ 1&1&-\lambda\end{array}\right) = -\lambda^3. \nonumber \]
Entonces no\(1\) es un valor propio en absoluto: ¡no hay vector de rango! La matriz de importancia no es estocástica porque la página no\(C\) tiene enlaces.
Considera el siguiente internet:
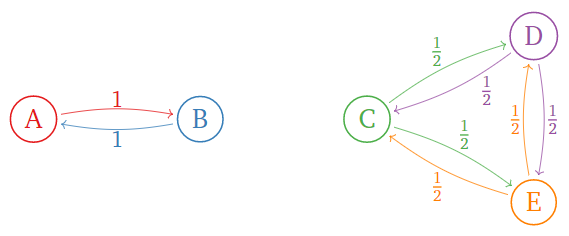
Figura\(\PageIndex{6}\)
La matriz de importancia es
\[\left(\begin{array}{ccccc}\color{Red}{0}&\color{blue}{1}&\color{black}{0}&0&0\\ \color{Red}{1}&\color{blue}{0}&\color{black}{0}&0&0 \\ 0&0&\color{Green}{0}&\color{Purple}{\frac{1}{2}}&\color{orange}{\frac{1}{2}} \\ 0&0&\color{Green}{\frac{1}{2}}&\color{Purple}{0}&\color{orange}{\frac{1}{2}} \\ 0&0&\color{Green}{\frac{1}{2}}&\color{Purple}{\frac{1}{2}}&\color{orange}{0}\end{array}\right).\nonumber\]
Esto tiene vectores propios linealmente independientes
\[\left(\begin{array}{c}1\\1\\0\\0\\0\end{array}\right)\quad\text{and}\quad\left(\begin{array}{c}0\\0\\1\\1\\1\end{array}\right),\nonumber\]
ambos con valor propio\(1\). Por lo que hay más de un vector de rango en este caso. Aquí la matriz de importancia es estocástica, pero no positiva.
Aquí está la solución de Page y Brin. Primero fijamos la matriz de importancia reemplazando cada columna cero por una columna de\(1/n\) s, donde\(n\) está el número de páginas:
\[A=\left(\begin{array}{ccc}0&0&0\\0&0&0\\1&1&0\end{array}\right)\quad\text{becomes}\quad A'=\left(\begin{array}{ccc}0&0&1/3 \\ 0&0&1/3 \\ 1&1&1/3\end{array}\right).\nonumber\]
La matriz de importancia modificada\(A'\) es siempre estocástica.
Ahora elegimos un número\(p\) en\((0,1)\text{,}\) llamado factor de amortiguación. (Un valor típico es\(p=0.15\).)
Dejar\(A\) ser la matriz de importancia para un internet con\(n\) páginas, y dejar\(A'\) ser la matriz de importancia modificada. La matriz de Google es la matriz
\[ M = (1-p)\cdot A' + p\cdot B \quad\text{where}\quad B = \frac 1n\left(\begin{array}{cccc}1&1&\cdot &1 \\ 1&1&\cdot &1 \\ \vdots&\vdots&\ddots&\vdots \\ 1&1&\cdots &1\end{array}\right). \nonumber \]
En la interpretación del surfista aleatorio, esta matriz\(M\) dice: con probabilidad\(p\text{,}\) nuestro surfista navegue a una página completamente aleatoria; de lo contrario, hará clic en un enlace aleatorio en la página actual, a menos que la página actual no tenga enlaces, en cuyo caso navegará a una página completamente aleatoria en cualquier caso. El lector puede verificar el siguiente hecho importante.
La Matriz de Google es una matriz estocástica positiva.
Si declaramos que los rangos de todas las páginas deben sumarse a\(1\text{,}\) entonces nos encontramos con:
El vector PageRank es el estado estacionario de la Matriz de Google.
Esto existe y tiene entradas positivas por el teorema de Perron-Frobenius. Lo difícil es calcularlo: en la vida real, la Matriz de Google tiene trillones de filas.
¿Cuál es el vector PageRank para el siguiente internet? (Utilice el factor de amortiguación\(p = 0.15\).)
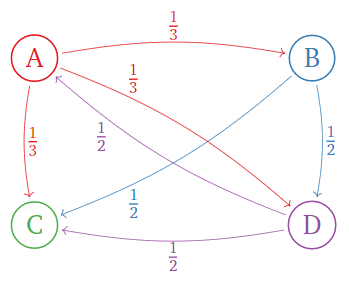
Figura\(\PageIndex{7}\)
¿Cuál es la página más importante? ¿Cuál es el menos importante?
Solución
Primero calculamos la matriz de importancia modificada:
\[A=\left(\begin{array}{cccc}\color{Red}{0}&\color{blue}{0}&\color{Green}{0}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{0}&\color{Green}{0}&\color{Purple}{0} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{0}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{0}&\color{Purple}{0}\end{array}\right) \quad\xrightarrow{\text{modify}}\quad A'=\left(\begin{array}{cccc}\color{Red}{0}&\color{blue}{0}&\color{Green}{\frac{1}{4}}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{0}&\color{Green}{\frac{1}{4}}&\color{Purple}{0} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{\frac{1}{4}}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{\frac{1}{4}}&\color{Purple}{0}\end{array}\right)\nonumber\]
Elegir el factor de amortiguación\(p=0.15\text{,}\) que es Google Matrix
\[\begin{align*} M &=0.85\cdot\left(\begin{array}{cccc}\color{Red}{0}&\color{blue}{0}&\color{Green}{\frac{1}{4}}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{0}&\color{Green}{\frac{1}{4}}&\color{Purple}{0} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{\frac{1}{4}}&\color{Purple}{\frac{1}{2}} \\ \color{Red}{\frac{1}{3}}&\color{blue}{\frac{1}{2}}&\color{Green}{\frac{1}{4}}&\color{Purple}{0}\end{array}\right)+0.15\cdot\left(\begin{array}{cccc}1/4&1/4&1/4&1/4 \\ 1/4&1/4&1/4&1/4 \\1/4&1/4&1/4&1/4 \\1/4&1/4&1/4&1/4 \end{array}\right) \\[4pt] &\approx\left(\begin{array}{cccc}0.0375& 0.0375& 0.2500 &0.4625\\ 0.3208& 0.0375& 0.2500& 0.0375\\ 0.3208& 0.4625 &0.2500& 0.4625\\ 0.3208 &0.4625& 0.2500& 0.0375\end{array}\right).\end{align*}\nonumber\]
El vector PageRank es el estado estacionario:
\[ w \approx \left(\begin{array}{c}0.2192\\ 0.1752 \\0.3558\\ 0.2498\end{array}\right) \nonumber \]
Este es el PageRank:
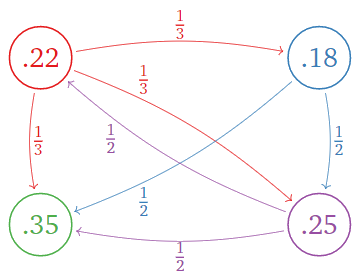
Figura\(\PageIndex{8}\)
La página\(C\) es la más importante, con un rango de\(0.558\text{,}\) y la página\(B\) es la menos importante, con un rango de\(0.1752.\)


