15.2: Cinemática de avance 2D
- Page ID
- 115475
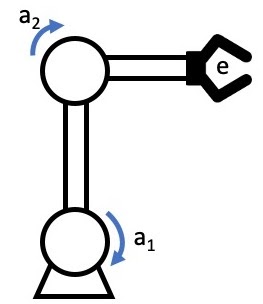
Este robot puede moverse en el\(x−y\) avión. Podemos representar la configuración del robot en su “Espacio Conjunto” conociendo los dos ángulos de articulación o\([a_1,a_2]\). Sin embargo lo que nos gustaría es representar la ubicación del extremo del robot (a menudo llamado el “efector final” o “mano”) en coordenadas “mundiales” (es decir,\(x−y\) sistema de coordenadas).
Hoy, utilizaremos Álgebra Lineal y matrices de transformación simples para intentar calcular cómo pasar de coordenadas “conjuntas” a coordenadas “mundiales”.
Robot de un solo eje
El siguiente código dibuja un robot simple de un solo eje (junta simple) con su articulación centrada en el origen y su ángulo inicial de cero con una longitud de brazo de robot de 4 “unidades” de largo.
Una matriz de rotación 2D alrededor del origen se define de la siguiente manera:
\ [\ begin {split}
\ left [\ begin {matrix}
x_ {end}\\
y_ {end}
\ end {matrix}
\ right]
=
\ left [\ begin {matrix}
\ cos (a) & -\ sin (a)\\
\ sin (a) &\ cos (qa
\ end {matrix}
\ right]
\ left [\ begin {matrix}
x_ {start}\\
y_ {start}
\ end {matrix}
\ right]
\ end {split}\ nonumber\]
La siguiente matriz de rotación girará el punto\(45^o\) alrededor del origen:
El siguiente código utiliza la función Jupyter interact y numpy para hacer una vista interactiva de lo anterior. Esto nos permite cambiar el valor del motor de rotación y ver cómo cambia el robot. La entrada a la función es el ángulo del eje y la salida son las\(x−y\) coordenadas.
Puede tomar algún tiempo para que la interacción se ponga al día. Intenta mover el deslizador lentamente...
def Robot_Simulator(q1=0):
a1 = q1/180 * np.pi
p0 = np.matrix([4,0]).T
p = p0
J1 = np.matrix([[np.cos(a1), -np.sin(a1)], [np.sin(a1), np.cos(a1)]])
p = np.concatenate( ( J1*p, np.matrix([0,0]).T), axis=1 )
plt.scatter(p[0,:].tolist()[0],p[1,:].tolist()[0], s=200, facecolors='none', edgecolors='r')
plt.scatter(0,0, s=200, facecolors='r', edgecolors='r')
plt.plot(p[0,:].tolist()[0],p[1,:].tolist()[0])
plt.axis('square')
plt.xlim([-5.5,5.5])
plt.ylim([-5.5,5.5])
ax = plt.gca()
plt.show()
return([ p[0,0], p[1,0] ])
p = interact(Robot_Simulator, q1=(-180,180,2));
Inspeccione el código anterior.
¿Qué línea del código define la matriz de transformación para la articulación del robot?
¿Qué línea de código define la longitud del brazo del robot?
Robot multieje
Ahora, consideremos el robot del video:
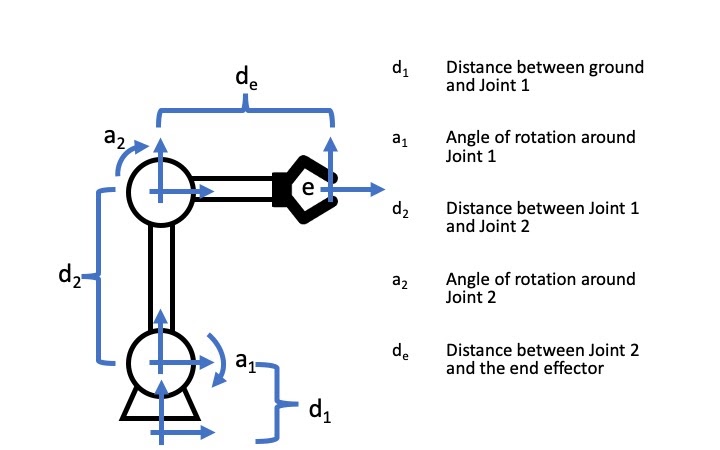
Observe que tiene dos juntas\(a_1\) y\(a_2\) y longitudes de desplazamiento de\(d_1\),\(d_2\) y\(d_e\). El espacio conjunto para este robot son solo sus ángulos\([a_1,a_2]\). Sin embargo, lo que queremos es conocer la ubicación del punto efector final\(p_e\) en la garra en el marco de referencia “mundial”, que la parte inferior más axies “en el suelo”.
En cada articulación, podemos definir un marco de referencia que gira y luego transforma el origen a la articulación ealier. Las matrices de transformación hacia adelante capturan la relación entre los marcos de referencia de diferentes enlaces del robot.
Por ejemplo, podemos pasar del motor base, o\(p_1\), marco de referencia al mundo, o\(p_w\), marco de referencia usando las siguientes ecuaciones:
\ [\ begin {split}
p_w
=
\ left [\ begin {matrix}
\ cos (a_1) & -\ sin (a_1)\\
\ sin (a_1) &\ cos (a_1)
\ end {matrix}
\ derecha]
p_1
+
\ left [\ begin {matrix}
0\\
d_1
\ fin {matriz}
\ derecha].
\ end {split}\ nonumber\]
La ecuación que se muestra arriba es un poco difícil de trabajar porque la parte\ (\ left [\ begin {matrix}
0\\
d_1
\ end {matrix}
\ right]\) hace que la ecuación no sea lineal (¿si no me crees? Recuerda las reglas para hacer lineal una función y aplícalas y compruébalo por ti mismo). Sin embargo, hay un truco fácil en Álgebra Lineal para convertir lo anterior en una matriz lineal grande. Este truco requiere que mantengamos un 1 (uno) extra por cada punto pero hace que las matemáticas funcionen muy bien. Básicamente el truco funciona de la siguiente manera:
\ [\ start {split}
\ left [\ begin {matrix}
x_w\\
y_w\\
1
\ end {matrix}
\ right]
=
\ left [\ begin {matrix}
cos (a_1) & -sin (a_1) & 0\\
sin ( a_1) & cos (a_1) & d_1\\
0 & 0 & 1
\ end {matriz}
\ derecha]
\ izquierda [\ comenzar {matriz}
x_1\\
y_1\\
1
\ end {matriz}
\ derecha]
\ fin {división}\ nonumber\]
Llamemos a la matriz de transformación para Joint 1,\(J_1\), y podemos reescribir las ecuaciones de la siguiente manera:
\[p_1 = J_1p_2 \nonumber \]
Por tu cuenta, escribe la multiplicación matricial anterior y convénzate de que es la misma que la anterior.
Ahora, podemos pasar del marco de\(p_2\) referencia al marco de\(p_1\) referencia básicamente la misma ecuación:
\ [\ start {split}
\ left [\ begin {matrix}
x_1\\
y_1\\
1
\ end {matrix}
\ right]
=
\ left [\ begin {matrix}
cos (a_2) & -sin (a_2) & d_2\\
sin (a_2) & cos (a_2) & 0\\
0 & 0 & 1
\ end {matriz}
\ derecha]
\ izquierda [\ comenzar {matriz}
x_2\\
y_2\\
1
\ end {matriz}
\ derecha]
\ end {split}\ nonumber\]
Para el último paso podemos hacer una transposición lineal simple desde el marco de\(p_e\) referencia del efector final al marco de\(p_2\) referencia:
\ [\ start {split}
\ left [\ begin {matrix}
x_2\\
y_2\\
1
\ end {matrix}
\ right]
=
\ left [\ begin {matrix}
1 & 0 & d_2\\
0 & 1 & 0 \\
0 & 0 & 1
\ end {matrix}
\ right]
\ left [\ begin {matrix}
x_e\\
y_e\\
1
\ end {matrix}
\ right]
\ end {split}\ nonumber\]
Si llamamos a cada matriz de transformación\(J_1\),\(J_2\),\(J_e\) entonces ojalá pueda ver que podemos encadenar estas matrices de transformación juntas de tal manera que obtengamos una sola transformación desde el efector final hasta las coordenadas mundiales de la siguiente manera:
\[p_w = J_1J_2J_ep_e \nonumber \]
Veamos cómo se ve esto en Python. Voy a usar numpy. La trama se vuelve un poco incómoda pero ojalá tenga sentido.
Primero, inicialicemos las variables a algunos números discretos:
A continuación, voy a definir un conjunto de puntos en el sistema de coordenadas del efector final. Estos puntos se escogen para formar una especie de forma de “C” diseñada para parecerse a un efector final. Los voy a trazar para que te ayuden a mostrarte a lo que me refiero:
El siguiente paso es aplicar la matriz de\(J_e\) transformación a los puntos de agarre que los colocará en el sistema de\(p_2\) coordenadas. Una vez transpuestos los puntos el código concatena el origen (0,0) en la lista de puntos para que podamos formar parte del brazo robot en la gráfica:
Esto lo hacemos de nuevo. Aplicar la matriz de\(J_2\) transformación para poner los puntos en el sistema de\(p_1\) coordenadas, concatenar el origen y trazar los resultados.
Lo hacemos una vez más. Aplicar la matriz de\(J_1\) transformación que pondrá los puntos en el sistema de\(p_w\) coordenadas, concatenar el origen y trazar los resultados. El resultado es un marco esquelético que representa a nuestro robot.
Modifique las variables de rotación a1 y a2 en el código anterior y vea si la nueva configuración del robot se ve bien.
HINTA asegúrese de que sus ángulos estén en radianes.
El siguiente es el mismo código que el anterior pero puesto en una función interactiva para que el código sea más fácil de jugar con:
from ipywidgets import interact
def Robot_Simulator(q1=0,q2=-0):
a1 = q1/180 * np.pi
a2 = q2/180 * np.pi
d1 = 0.5
d2 = 3
de = 3
target = np.matrix([-3,2, 1])
print(target)
pe = np.matrix([[1, 0.5, 1],[0,0.5,1],[0,-0.5, 1],[1,-0.5, 1],[0,-0.5, 1],[0,0, 1]]).T
Je = np.matrix([[1, 0, de],
[0, 1, 0],
[0,0,1]])
p = np.concatenate( ( Je*pe, np.matrix([0,0,1]).T), axis=1 )
J2 = np.matrix([[np.cos(a2), -np.sin(a2), 0],
[np.sin(a2), np.cos(a2), d2],
[0,0,1]])
p = np.concatenate( ( J2*p, np.matrix([0,0,1]).T), axis=1 )
J1 = np.matrix([[np.cos(a1), -np.sin(a1), 0],
[np.sin(a1), np.cos(a1), d1],
[0,0,1]])
p = np.concatenate( ( J1*p, np.matrix([0,0,1]).T), axis=1 )
plt.scatter(p[0,:].tolist()[0],p[1,:].tolist()[0], s=20, facecolors='none', edgecolors='r')
plt.scatter(0,0, s=20, facecolors='r', edgecolors='r')
plt.plot(p[0,:].tolist()[0],p[1,:].tolist()[0])
plt.plot(target[0,0], target[0,1],'*')
plt.axis('scaled')
plt.xlim([-8,8])
plt.ylim([-8,8])
plt.show()
target = interact(Robot_Simulator, q1=(-180,180), q2=(-180,180));
[[-3 2 1]]
Si la trama de interacción es realmente entrecortada en su máquina esto se debe a que la función se está actualizando constantemente a medida que mueve los controles deslizantes. Considera reemplazar la función interact por interact_manual para eliminar las actualizaciones continuas. Tendrás que cambiar el código de importación en la línea 1.
Mueve el robot anterior para que el efector final esté “agarrando” el objetivo (estrella amarilla/anaranjada). Observe que hay más de un punto en el “espacio conjunto” que da la misma respuesta. Este es el problema cinemático inverso (que es más difícil). Sabemos el punto que queremos pero necesitamos encontrar las articulaciones que pongan al robot en ese punto.
El código en la siguiente celda se corta y pega desde arriba. Modifique el código para agregar un tercer Joint al robot.
from ipywidgets import interact
def Robot_Simulator(q1=0,q2=-0):
a1 = q1/180 * np.pi
a2 = q2/180 * np.pi
#####Start your code here #####
#####End of your code here#####
d1 = 0.5
d2 = 3
de = 3
#####Start your code here #####
#####End of your code here#####
target = np.matrix([-3,2, 1])
print(target)
pe = np.matrix([[1, 0.5, 1],[0,0.5,1],[0,-0.5, 1],[1,-0.5, 1],[0,-0.5, 1],[0,0, 1]]).T
Je = np.matrix([[1, 0, de],
[0, 1, 0],
[0,0,1]])
p = np.concatenate( ( Je*pe, np.matrix([0,0,1]).T), axis=1 )
#####Start your code here #####
#####End of your code here#####
J2 = np.matrix([[np.cos(a2), -np.sin(a2), 0],
[np.sin(a2), np.cos(a2), d2],
[0,0,1]])
p = np.concatenate( ( J2*p, np.matrix([0,0,1]).T), axis=1 )
J1 = np.matrix([[np.cos(a1), -np.sin(a1), 0],
[np.sin(a1), np.cos(a1), d1],
[0,0,1]])
p = np.concatenate( ( J1*p, np.matrix([0,0,1]).T), axis=1 )
plt.scatter(p[0,:].tolist()[0],p[1,:].tolist()[0], s=20, facecolors='none', edgecolors='r')
plt.scatter(0,0, s=20, facecolors='r', edgecolors='r')
plt.plot(p[0,:].tolist()[0],p[1,:].tolist()[0])
plt.plot(target[0,0], target[0,1],'*')
plt.axis('scaled')
plt.xlim([-8,8])
plt.ylim([-8,8])
plt.show()
target = interact(Robot_Simulator, q1=(-180,180), q2=(-180,180));
[[-3 2 1]]
Vuelva a hacer la cinemática inversa, y encuentre tres ángulos que coloquen al robot sobre la estrella.