Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

20.2: Introducción a los modelos de Markov

Última actualización

30 oct 2022
Guardar como PDF
- 20.1: Revisión previa a la clase
- 20.3: Otro ejemplo de modelo de Markov

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

If you have already signed in, please refresh the page.

%matplotlib inline
import matplotlib.pylab as plt
import numpy as np
import sympy as sym
sym.init_printing(use_unicode=True)
from urllib.request import urlretrieve

urlretrieve('https://raw.githubusercontent.com/colbrydi/jupytercheck/master/answercheck.py', 
            'answercheck.py');

%matplotlib inline
import matplotlib.pylab as plt
import numpy as np
import sympy as sym
sym.init_printing(use_unicode=True)
from urllib.request import urlretrieve

urlretrieve('https://raw.githubusercontent.com/colbrydi/jupytercheck/master/answercheck.py', 
            'answercheck.py');

En teoría de probabilidad, un modelo de Markov es un modelo estocástico utilizado para modelar sistemas que cambian aleatoriamente. Se supone que los estados futuros dependen únicamente del estado actual, no de los hechos ocurridos antes de él.

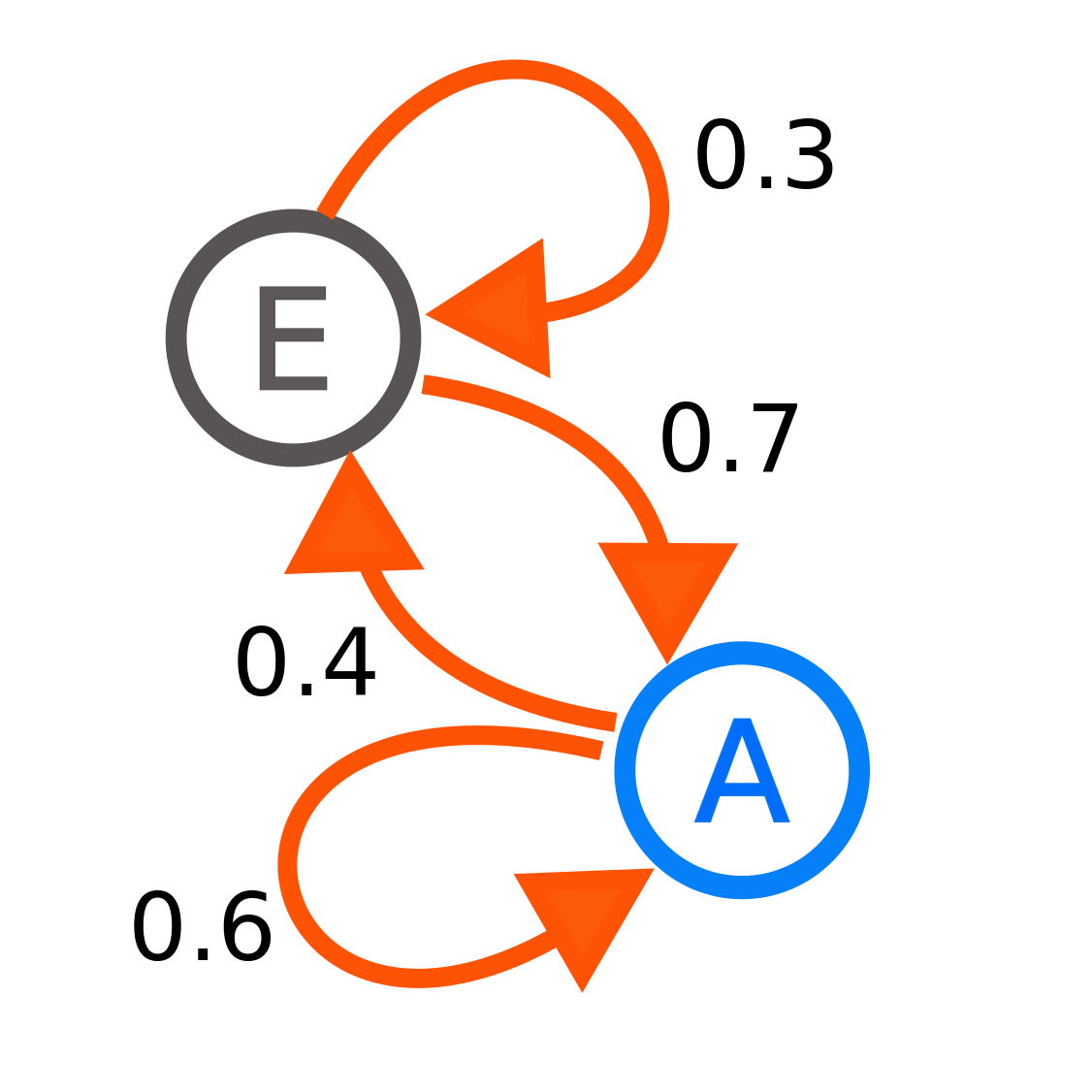
Un modelo de Markov. — Un diagrama que representa un proceso de Markov de dos estados, con los estados etiquetados E y A. Vía Wikipedia

Cada número representa la probabilidad de que el proceso de Markov cambie de un estado a otro, con la dirección indicada por la flecha. Por ejemplo, si el proceso de Markov está en el estado A, entonces la probabilidad de que cambie al estado E es 0.4, mientras que la probabilidad de que permanezca en el estado A es 0.6.

El modelo de estado anterior puede ser representado por una matriz de transición.

\ [\ begin {split}\ begin {array} {cc}
&\ text {Estado actual}\\
P = &
\ begin {bmatrix}
p_ {A\ rightarrow A} & p_ {E\ rightarrow A}\\
p_ {A\ rightarrow E} & p_ {E\ rightarrow E}
\ end {bmatrix}
\ end {array}
\ text {siguiente estado}\ end {split}\ nonumber\]

En otras palabras podemos escribir lo anterior de la siguiente manera

If you have already signed in, please refresh the page.

A = np.matrix([[0.6, 0.7],[0.4, 0.3]])
sym.Matrix(A)

A = np.matrix([[0.6, 0.7],[0.4, 0.3]])
sym.Matrix(A)

Observe cómo las columnas de la matriz se suman a una. Esto se debe a que todas las probabilidades de transición fuera de una matriz deben sumar al 100 por ciento.

Ahora, considera el siguiente mapa de casas con gatos en cada habitación...

En cada paso de tiempo, existe la misma probabilidad de que un gato se quede en su habitación actual o se mude a una nueva habitación. Si un gato elige salir de una habitación, entonces existe la misma posibilidad de que ese gato recoja alguna de las puertas de la habitación para salir.

Hacer esto

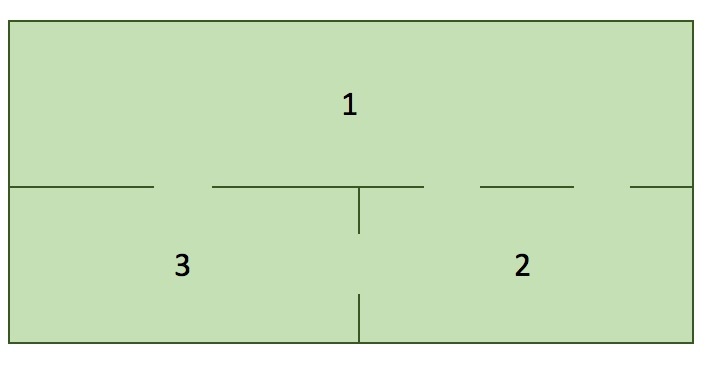
Trate de dibujar una cadena de Markov (matriz de Markov) para el sistema de ecuaciones anterior. Prepárate para compartir tu diagrama con la clase.

Una cadena de Markov se puede representar como un modelo de transición de Markov de la forma $Ax=b$ . ¿Dónde $A$ está su matriz de tranisición de probabilidad (a menudo representada como una $P$ en lugar de una $A$ ). $x$ es el estado antes de la transición y $b$ es el estado después de la transición.

Pregunta

Generar un modelo de transición de Markov representado como una matriz $P$ de la forma:

\ [
\ begin {array} {ccc}
&\ text {Sala actual}\\
P = &
\ begin {bmatrix}
p_ {11} & p_ {12} & p_ {13}\\
p_ {21} & p_ {22} & p_ {23}\\
p_ {31} & p_ {32} & p_ {33}
\ end {bmatrix}
\ end {array}
\ text {Next Room}\ nonumber\]

Dónde $p_{ij}$ están las transiciones de probabilidad del gato moviéndose entre habitaciones (de habitación $j$ a habitación $i$ ):

If you have already signed in, please refresh the page.

##put your answer here

##put your answer here

If you have already signed in, please refresh the page.

from answercheck import checkanswer

checkanswer.matrix(P,'1001a6fa07727caf8ce05226b765542c');

from answercheck import checkanswer

checkanswer.matrix(P,'1001a6fa07727caf8ce05226b765542c');

Pregunta

Supongamos que el sistema comienza con; 6 gatos en la habitación 1, 15 gatos en la habitación 2 y 3 gatos en la habitación 3. ¿Cuántos gatos habrá en cada habitación después de un paso de tiempo (Almacenar los valores en un vector llamado current_state)?

If you have already signed in, please refresh the page.

#Put your answer to the above question here.

#Put your answer to the above question here.

If you have already signed in, please refresh the page.

from answercheck import checkanswer

checkanswer.vector(current_state,'98d5519be82a0585654de5eda3a7f397');

from answercheck import checkanswer

checkanswer.vector(current_state,'98d5519be82a0585654de5eda3a7f397');

Pregunta

El siguiente código trazará el número de gatos en función de time ( $t$ ). Cuando este sistema converge, ¿cuál es el estado estacionario?

If you have already signed in, please refresh the page.

#Define Start State
room1 = [6]
room2 = [15]
room3 = [3]

current_state = np.matrix([room1, room2, room3])

for i in range(10):
    #update Current State
    current_state = P*current_state
    
    #Store history for each room
    room1.append(current_state[0])
    room2.append(current_state[1])
    room3.append(current_state[2])
    
plt.plot(room1, label="room1");
plt.plot(room2, label="room2");
plt.plot(room3, label="room3");
plt.legend();
print(current_state)

#Define Start State
room1 = [6]
room2 = [15]
room3 = [3]

current_state = np.matrix([room1, room2, room3])

for i in range(10):
    #update Current State
    current_state = P*current_state
    
    #Store history for each room
    room1.append(current_state[0])
    room2.append(current_state[1])
    room3.append(current_state[2])
    
plt.plot(room1, label="room1");
plt.plot(room2, label="room2");
plt.plot(room3, label="room3");
plt.legend();
print(current_state)

Pregunta

Calcula los valores propios y los vectores propios de tu matriz de $P$ transición.

If you have already signed in, please refresh the page.

##put your answer here

##put your answer here

Hacer esto

Haz un nuevo vector llamado steadystate a partir del vector propio de tu $P$ matriz con un valor propio de 1.

If you have already signed in, please refresh the page.

## Put your answer here

## Put your answer here

Dado que los vectores de estado estacionario representan probabilidades a largo plazo, deben sumar a uno (1). Sin embargo, la mayoría de las bibliotecas de programación (por ejemplo, numpy y sympy) devuelven vectores propios “normalizados” a una longitud de 1 (es decir, norm (e) ==1).

Hacer esto

Correcto para la normalización multiplicando el vector propio de estado estacionario por una constante tal que la suma de los elementos vectoriales se sume a 1.

If you have already signed in, please refresh the page.

#Put your answer here

#Put your answer here

Hacer esto

Piensa en el problema de los gatos, porque un gato tiene que estar en una de las tres habitaciones. Eso significa que el número total de gatos no cambiará. Si sumamos el número de gatos en todas las habitaciones juntos, este número tiene que ser el mismo. Por lo tanto, si arrancamos voluntad 6+15+3=24 gatos, también hay 24 gatos en el estado estacionario. Modifique el estado estacionario para asegurarse de que el número total de gatos sea 24.

Pregunta

¿Por qué la suma de los números en cada etapa sigue siendo la misma?

Hacer esto

Pregunta

Pregunta

Pregunta

Pregunta

Hacer esto

Hacer esto

Hacer esto

Pregunta

Support Center

How can we help?