5.3: Visualizando Vectores- Vectores en Tres Dimensiones
- Page ID
- 116567
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- T/F: El punto de vista del lector marca la diferencia en cómo se ven los vectores en 3D.
- T/F: Si dos vectores no están cerca uno del otro, entonces no parecerán estar cerca uno del otro cuando se graficen.
- T/F: La ley del paralelogramo sólo se aplica para sumar vectores en 2D.
Terminamos la última sección afirmando que podríamos extender las ideas de dibujar vectores 2D a dibujar vectores 3D. Una vez que entendemos cómo dibujar correctamente estos vectores, la suma y resta es relativamente fácil. También discutiremos cómo encontrar la longitud de un vector en 3D.
Comenzamos con los conceptos básicos de dibujar un vector en 3D. En lugar de tener solo los\(y\) ejes tradicionales\(x\) y, ahora agregamos un tercer eje, el\(z\) eje. Sin ningún vector adicional, se puede ver un sistema de coordenadas 3D genérico en la Figura\(\PageIndex{1}\).
Figura\(\PageIndex{1}\): El sistema de coordenadas 3D
En 2D, el punto\((2,1)\) se refiere a ir 2 unidades en la\(x\) dirección seguida de 1 unidad en la\(y\) dirección. En 3D, cada punto es referenciado por 3 coordenadas. El punto\((4,2,3)\) se encuentra yendo 4 unidades en\(x\) dirección,\(2\) unidades en\(y\) dirección, y 3 unidades en\(z\) dirección.
¿Cómo se dibuja un vector en este sistema de coordenadas? Como cabría esperar, podemos bosquejar el vector\(\vec{v}=\left[\begin{array}{c}{1}\\{2}\\{3}\end{array}\right]\) dibujando una flecha desde el origen (el punto (0,0,0)) hasta\((1,2,3)\).\(^{1}\) el punto La única parte “complicada” proviene del hecho de que estamos tratando de representar el espacio tridimensional en una hoja de papel bidimensional. Sin embargo, no es realmente difícil. Descubriremos una buena manera de abordar esto en el contexto de un ejemplo.
Esboce los siguientes vectores con su origen en el origen.
\[\vec{v}=\left[\begin{array}{c}{2}\\{1}\\{3}\end{array}\right]\quad\text{and}\quad\vec{u}=\left[\begin{array}{c}{1}\\{3}\\{-1}\end{array}\right] \nonumber \]
Solución
Empezaremos con\(\vec{v}\) primero. Comenzando por el origen, mover\(2\) las unidades en la\(x\) dirección. Esto nos pone en el punto\((2,0,0)\) del\(x\) eje. Después, mueva\(1\) la unidad en la\(y\) dirección. (En nuestro método de dibujo, esto significa mover la\(1\) unidad directamente hacia la derecha. Por supuesto, no tenemos una grilla a seguir, así que tenemos que hacer una buena aproximación de esta distancia.) Por último, movemos\(3\) unidades en la\(z\) dirección. (Nuevamente, en nuestro dibujo, esto significa ir directamente “arriba”\(3\) unidades, y debemos usar nuestro mejor juicio en un boceto para medirlo).
Esto nos permite ubicar el punto\((2,1,3)\); ahora dibujamos una flecha desde el origen hasta este punto. En Figura\(\PageIndex{2}\) tenemos todas las\(4\) etapas de este boceto. Las líneas discontinuas nos muestran moviéndonos hacia abajo del\(x\) eje en (a); en (b) nos movemos en la\(y\) dirección; en (c) nos movemos hacia arriba en la\(z\) dirección, y finalmente en (d) se dibuja la flecha.
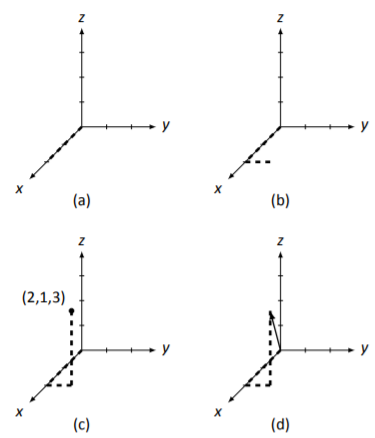
Figura\(\PageIndex{2}\): Etapas de bosquejar el vector\(\vec{v}\) para Ejemplo\(\PageIndex{1}\).
Dibujar las líneas discontinuas nos ayuda a encontrar nuestro camino en nuestra representación del espacio tridimensional. Sin ellos, es difícil ver qué tan lejos en cada dirección se supone que ha ido el vector.
Para dibujar\(\vec{u}\), seguimos el mismo procedimiento que usamos para dibujar\(\vec{v}\). Primero localizamos el punto\((1,3,-1)\), luego dibujamos la flecha apropiada. En Figura\(\PageIndex{3}\) hemos\(\vec{u}\) dibujado junto con\(\vec{v}\). Hemos utilizado diferentes líneas discontinuas y punteadas para cada vector para ayudar a distinguirlos.
Observe que esta vez tuvimos que ir en\(z\) dirección negativa; esto solo significa que bajamos una unidad en lugar de subir una unidad.
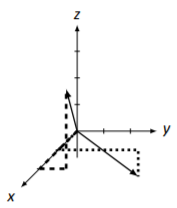
Figura\(\PageIndex{3}\): Vectores\(\vec{v}\) y\(\vec{u}\) en Ejemplo\(\PageIndex{1}\).
Como en 2D, no solemos dibujar el vector cero,
\[\vec{0}=\left[\begin{array}{c}{0}\\{0}\\{0}\end{array}\right]. \nonumber \]
No apunta a ninguna parte. Se trata de un vector conceptualmente importante que no tiene una visualización terriblemente interesante.
Nuestro método de dibujar objetos 3D sobre una superficie plana, una superficie 2D, es bastante inteligente. Sin embargo, no es perfecto; visualmente, dibujar vectores con componentes negativos (especialmente\(x\) coordenadas negativas) puede parecer un poco extraño. Además, dos vectores muy diferentes pueden apuntar al mismo lugar. Destacaremos esto con nuestros siguientes dos ejemplos.
Dibuja el vector\(\vec{v}=\left[\begin{array}{c}{-3}\\{-1}\\{2}\end{array}\right].\)
Solución
Utilizamos el mismo procedimiento que usamos en Ejemplo\(\PageIndex{1}\). Comenzando por el origen, nos movemos en las\(3\) unidades de\(x\) dirección negativa, luego\(1\) unidad en\(y\) dirección negativa, y luego finalmente subimos\(2\) unidades en la\(z\) dirección para encontrar el punto\((-3,-1,2)\). Seguimos dibujando una flecha. Nuestro boceto se encuentra en la Figura\(\PageIndex{4}\);\(\vec{v}\) se dibuja en dos sistemas de coordenadas, uno con las líneas discontinuas útiles, y otro sin. El segundo dibujo deja bastante claro que las líneas discontinuas son realmente útiles.
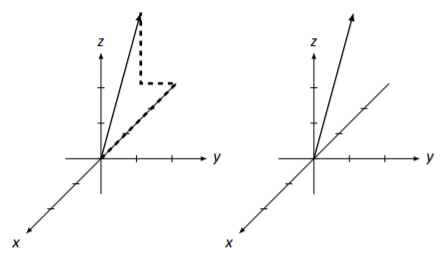
Figura\(\PageIndex{4}\): Vector\(\vec{v}\) en Ejemplo\(\PageIndex{2}\).
Dibuja los vectores\(\vec{v}=\left[\begin{array}{c}{2}\\{4}\\{2}\end{array}\right]\) y\(\vec{u}=\left[\begin{array}{c}{-2}\\{1}\\{-1}\end{array}\right]\) en el mismo sistema de coordenadas.
Solución
Seguimos los pasos que hemos dado antes para bosquejar estos vectores, mostrados en la Figura\(\PageIndex{5}\). Las líneas discontinuas son ayudantes\(\vec{v}\) y las líneas punteadas son ayudas para\(\vec{u}\). Nuevamente incluimos los vectores sin las líneas discontinuas y punteadas; pero sin éstas, ¡es muy difícil decir qué vector es cuál!
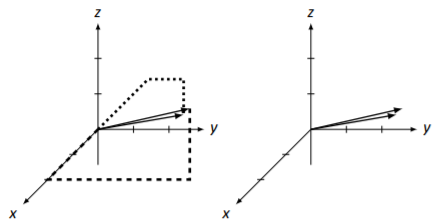
Figura\(\PageIndex{5}\): Vectores\(\vec{v}\) y\(\vec{u}\) en Ejemplo\(\PageIndex{3}\).
Nuestros tres ejemplos han demostrado que tenemos un método bastante inteligente, aunque imperfecto, para dibujar vectores 3D. Los vectores en Ejemplo\(\PageIndex{3}\) se parecen debido a nuestro punto de vista. En la Figura\(\PageIndex{6}\) (a), hemos girado los ejes de coordenadas, dando a los vectores una apariencia diferente. (Vector\(\vec{v}\) ahora parece que se encuentra en el\(y\) eje.)
Otro factor importante en cómo se ven las cosas es la escala que utilizamos para los\(z\) ejes\(x\)\(y\),, y. En 2D, es fácil hacer que la escala sea uniforme para ambos ejes; en 3D, puede ser un poco complicado hacer que la escala sea igual en los ejes que están “inclinados”. La Figura\(\PageIndex{6}\) (b) muestra nuevamente los mismos\(2\) vectores encontrados en Ejemplo\(\PageIndex{3}\), pero esta vez la escala del\(x\) eje es un poco diferente. El resultado final es que nuevamente los vectores aparecen un poco diferentes a lo que hacían antes. Estos hechos no necesariamente plantean un gran problema; simplemente debemos ser conscientes de estos hechos y no hacer juicios sobre objetos 3D basados en una sola imagen 2D. \(^{2}\)
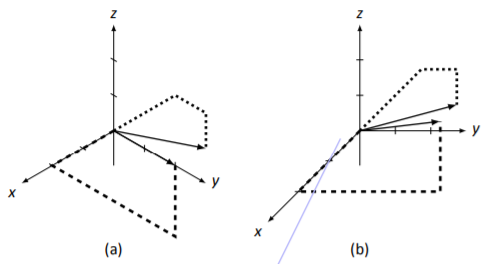
Figura\(\PageIndex{6}\): Vectores\(\vec{v}\) y\(\vec{u}\) en Ejemplo\(\PageIndex{3}\) con un punto de vista diferente (a) y escala de\(x\) eje (b).
Ahora investigamos las propiedades de la aritmética vectorial: ¿qué sucede (es decir, cómo dibujamos) cuando agregamos vectores 3D y multiplicamos por un escalar? ¿Cómo calculamos la longitud de un vector 3D?
Sumas y restas de vectores
En 2D, vimos que podíamos sumar vectores juntos gráficamente usando la Ley de Paralelogramo. ¿Lo mismo se aplica para agregar vectores en 3D? Investigamos en un ejemplo.
Dejar\(\vec{v}=\left[\begin{array}{c}{2}\\{1}\\{3}\end{array}\right]\) y\(\vec{u}=\left[\begin{array}{c}{1}\\{3}\\{-1}\end{array}\right]\). Croquis\(\vec{v}+\vec{u}\).
Solución
Se esbozó cada uno de estos vectores previamente en Ejemplo\(\PageIndex{1}\). Los dibujamos, junto con\(\vec{v}+\vec{u} = \left[\begin{array}{c}{3}\\{4}\\{2}\end{array}\right]\), en la Figura\(\PageIndex{7}\) (a). (Utilizamos líneas discontinuas sueltas para\(\vec{v}+\vec{u}\).)
¿Todavía se mantiene la Ley de Paralelogramo? En la Figura\(\PageIndex{7}\) (b), dibujamos representaciones adicionales de\(\vec{v}\) y\(\vec{u}\) para formar un paralelogramo (sin todas las líneas punteadas), lo que parece afirmar el hecho de que la Ley del Paralelogramo sí sostiene.
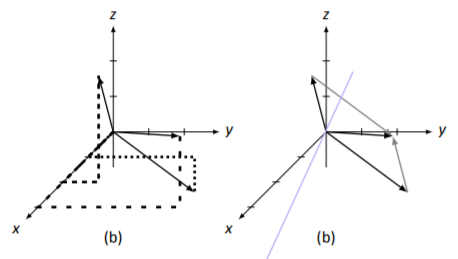
Figura\(\PageIndex{7}\): Vectores\(\vec{v}\),\(\vec{u}\), y\(\vec{v}+\vec{u}\) Ejemplo\(\PageIndex{4}\).
También aprendimos que en 2D, podríamos restar vectores dibujando un vector de la punta de un vector a otro. \(^{3}\)¿Esto también funciona en 3D? Volveremos a investigar con un ejemplo, usando los vectores familiares\(\vec{v}\) y\(\vec{u}\) de antes.
Dejar\(\vec{v}=\left[\begin{array}{c}{2}\\{1}\\{3}\end{array}\right]\) y\(\vec{u}=\left[\begin{array}{c}{1}\\{3}\\{-1}\end{array}\right]\). Croquis\(\vec{v}-\vec{u}\).
Solución
Es sencillo computar eso\(\vec{v}-\vec{u}=\left[\begin{array}{c}{1}\\{-2}\\{4}\end{array}\right]\). Los tres vectores se esbozan en la Figura\(\PageIndex{8}\) (a), donde de nuevo\(\vec{v}\) es guiado por las líneas discontinuas,\(\vec{u}\) punteadas y\(\vec{v}-\vec{u}\) discontinuas sueltas.
¿Todavía se mantiene la regla de resta 2D? Es decir, ¿podemos dibujar\(\vec{v} -\vec{u}\) dibujando una flecha desde la punta de\(\vec{u}\) hasta la punta de\(\vec{v}\)? En la Figura\(\PageIndex{8}\) (b), traducimos el dibujo de\(\vec{v}-\vec{u}\) a la punta de\(\vec{u}\), y efectivamente, parece que funciona. (Y de hecho, realmente lo hace).
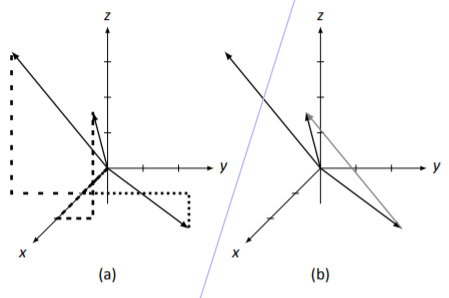
Figura\(\PageIndex{8}\): Vectores\(\vec{v}\),\(\vec{u}\), y\(\vec{v}-\vec{u}\) del Ejemplo\(\PageIndex{5}\).
Los dos ejemplos anteriores resaltan el hecho de que incluso en 3D, podemos bosquejar vectores sin saber explícitamente cuáles son. Practicamos esto una vez más en el siguiente ejemplo.
Los vectores\(\vec{v}\) y\(\vec{u}\) se dibujan en la Figura\(\PageIndex{9}\). Usando este dibujo, bosquejar los vectores\(\vec{v}+\vec{u}\) y\(\vec{v}-\vec{u}\).
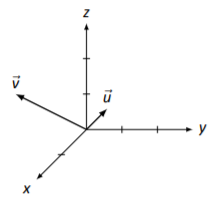
Figura\(\PageIndex{9}\): Vectores\(\vec{v}\) y\(\vec{u}\) por Ejemplo\(\PageIndex{6}\).
Solución
Usando la Ley del Paralelogramo, dibujamos\(\vec{v}+\vec{u}\) dibujando primero una versión gris de\(\vec{u}\) proveniente de la punta de\(\vec{v}\);\(\vec{v}+\vec{u}\) se dibuja discontinua en la Figura\(\PageIndex{10}\).
Para dibujar\(\vec{v}-\vec{u}\), dibujamos una flecha punteada desde la punta de\(\vec{u}\) hasta la punta de\(\vec{v}\).
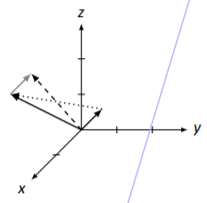
Figura\(\PageIndex{10}\): Vectores\(\vec{v}\),\(\vec{u}\),\(\vec{v}+\vec{u}\) y\(\vec{v}-\vec{u}\) por Ejemplo\(\PageIndex{6}\).
Multiplicación escalar
Dado un vector\(\vec{v}\) en 3D, ¿cómo se\(2\vec{v}\) ve el vector? ¿Qué tal\(-\vec{v}\)? Después de aprender sobre la suma y resta de vectores en 3D, probablemente estamos ganando confianza en trabajar en 3D y estamos tentados a decir que\(2\vec{v}\) es un vector el doble de largo que\(\vec{v}\), apuntando en la misma dirección, y\(-\vec{v}\) es un vector de la misma longitud que\(\vec{v}\), apuntando en la dirección opuesta. Estaríamos en lo cierto. Esto lo demostramos en el siguiente ejemplo.
Sketch\(\vec{v}\)\(2\vec{v}\), y\(-\vec{v}\), donde
\[\vec{v}=\left[\begin{array}{c}{1}\\{2}\\{3}\end{array}\right]. \nonumber \]
Solución
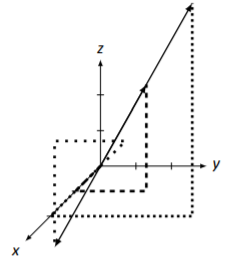
Figura\(\PageIndex{11}\): Croquizar múltiplos escalares de\(\vec{v}\) en Ejemplo\(\PageIndex{7}\).
Es fácil de calcular
\[2\vec{v}=\left[\begin{array}{c}{2}\\{4}\\{6}\end{array}\right]\quad\text{and}\quad -\vec{v}=\left[\begin{array}{c}{-1}\\{-2}\\{-3}\end{array}\right]. \nonumber \]
Estos se dibujan en la Figura\(\PageIndex{11}\). Esta figura es, en muchos sentidos, un desastre, con todas las líneas discontinuas y punteadas. Sin embargo, son útiles. Úselos para ver cómo se formó cada vector, y tenga en cuenta que al\(2\vec{v}\) menos se ve el doble de largo que\(\vec{v}\), y se ve como\(-\vec{v}\) puntos en la dirección opuesta. \(^{4}\)
Longitud del vector
¿Cómo medimos la longitud de un vector en 3D? En 2D, pudimos responder a esta pregunta usando el Teorema de Pitágoras. ¿Se aplica el Teorema de Pitágoras en 3D? En cierto sentido, lo hace.
Considera el vector\(\vec{v}=\left[\begin{array}{c}{1}\\{2}\\{3}\end{array}\right]\), tal como se dibuja en la Figura\(\PageIndex{12}\) (a), con líneas punteadas guía. Ahora mira la parte (b) de la misma figura. Observe cómo dos longitudes de las líneas discontinuas ahora se han dibujado de color gris, y se ha agregado otra línea punteada.
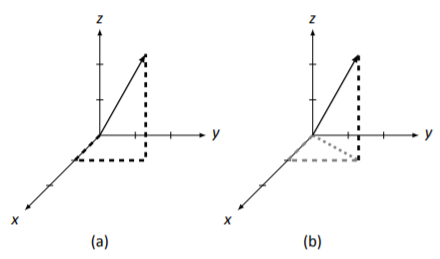
Figura\(\PageIndex{12}\): Cálculo de la longitud de\(\vec{v}\)
Estas líneas discontinuas y punteadas grises forman un triángulo rectángulo con la línea punteada formando la hipotenusa. Podemos encontrar la longitud de la línea punteada usando el Teorema de Pitágoras.
\[\text{length of the dotted line} = \sqrt{ \text{sum of the squares of the dashed line lengths}} \nonumber \]
Es decir, la longitud de la línea punteada =\(\sqrt{1^2 + 2^2} = \sqrt{5}\).
Ahora consideremos esto: el vector\(\vec{v}\) es la hipotenusa de otro triángulo rectángulo: el formado por la línea punteada y la línea discontinua vertical. Nuevamente, empleamos el Teorema de Pitágoras para encontrar su longitud.
\[\text{length of } \vec{v} = \sqrt{ \text{(length of dashed gray line)}^2 + \text{(length of black dashed line)}^2} \nonumber \]
Así, la longitud de\(\vec{v}\) es (recordar, denotamos la longitud de\(\vec{v}\) con\(||\vec{v}||\)):
\[\begin{align}\begin{aligned} ||\vec{v}|| &= \sqrt{\text{(length of gray line)}^2 + \text{(length of black line)}^2} \\ &= \sqrt{ \sqrt{5}^2 + 3^2}\\ &= \sqrt{ 5 + 3^2}\\\end{aligned}\end{align} \nonumber \]
Detengámonos un momento y pensemos: ¿de dónde\(5\) vino esto en la ecuación anterior? Vino de encontrar la longitud de la línea discontinua gris —de la que vino\(1^2+2^2\). Sustituyamos eso en la ecuación anterior:
\[\begin{align}\begin{aligned} ||\vec{v}|| &= \sqrt{5+ 3^2} \\ &= \sqrt{1^2+2^2+3^2}\\ &= \sqrt{14}\\\end{aligned}\end{align} \nonumber \]
La clave viene de la ecuación media:\(||\vec{v}|| = \sqrt{1^2+2^2+3^2}\). ¿Esos números 1, 2 y 3 parecen familiares? Ellos son los valores componentes de\(\vec{v}\)! Esto es muy similar a la definición de la longitud de un vector 2D. Después de definirlo formalmente, practicaremos con un ejemplo.
Let
\[\vec{v}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\end{array}\right]. \nonumber \]
La longitud de\(\vec{v}\), denotado\(||\vec{v}||\), es
\[||\vec{v}||=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}. \nonumber \]
Encuentra las longitudes de los vectores\(\vec{v}\) y\(\vec{u}\), dónde
\[\vec{v}=\left[\begin{array}{c}{2}\\{-3}\\{5}\end{array}\right]\quad\text{and}\quad\vec{u}=\left[\begin{array}{c}{-4}\\{7}\\{0}\end{array}\right]. \nonumber \]
Solución
Aplicamos Definición Longitud de Vector 3D a cada vector:
\[\begin{align}\begin{aligned} ||\vec{v}|| &= \sqrt{2^2 + (-3)^2 + 5^2} \\ &= \sqrt{4 + 9 + 25}\\ &= \sqrt{38}\\ \\ ||\vec{u}|| &= \sqrt{(-4)^2 + 7^2 + 0^2}\\ &= \sqrt{16+49}\\ &= \sqrt{65}\end{aligned}\end{align} \nonumber \]Aquí terminamos nuestra investigación sobre el mundo de graficar vectores. Se pueden hacer extensiones para graficar vectores 4D y más allá, pero realmente son confusas y no se hacen realmente excepto para fines abstractos.
Sin embargo, hay más cosas que explorar. Al igual que en 2D, podemos transformar el espacio 3D por multiplicación matricial. Hacer esto correctamente (rotar, estirar, cizallar, etc.) permite manipular el espacio 3D y crear increíbles gráficos por computadora.
Notas al pie
[1] Por supuesto, no tenemos que comenzar por el origen; lo único que realmente importa es que la punta de la flecha sea\(1\) unidad en la\(x\) dirección,\(2\) unidades en la\(y\) dirección, y\(3\) unidades en la\(z\) dirección desde la origen de la flecha.
[2] El cerebro humano usa ambos ojos para transmitir información 3D, o profundidad. Con un ojo cerrado (o faltante), podemos pasar un momento muy difícil con la “percepción de profundidad”. Dos objetos que están muy separados pueden parecer muy cercanos entre sí. Un ejemplo sencillo de este problema es este: cierra un ojo, y coloca tu dedo índice alrededor de un pie por encima de este texto, directamente encima de esta PALABRA. A ver si estabas en lo correcto dejando caer el dedo hacia abajo. ¿De verdad golpeaste el lugar adecuado? Inténtalo de nuevo con ambos ojos, y deberías ver una diferencia notable en tu precisión.
Mirar objetos 3D en papel es un poco como ver el mundo con un ojo cerrado.
[3] Recordemos que es importante qué vector utilizamos para el origen y cuál se utilizó para la punta.
[4] Nuestro trabajo anterior demostró que las miradas pueden ser engañosas, pero de hecho es cierto en este caso.