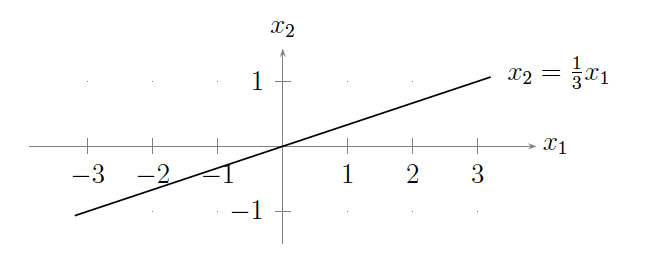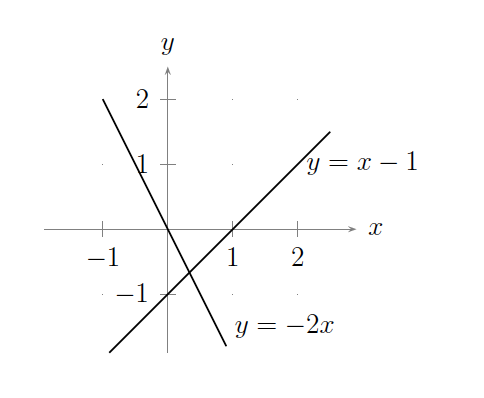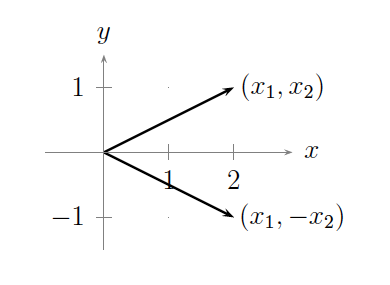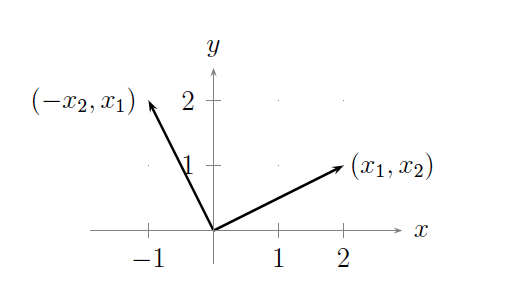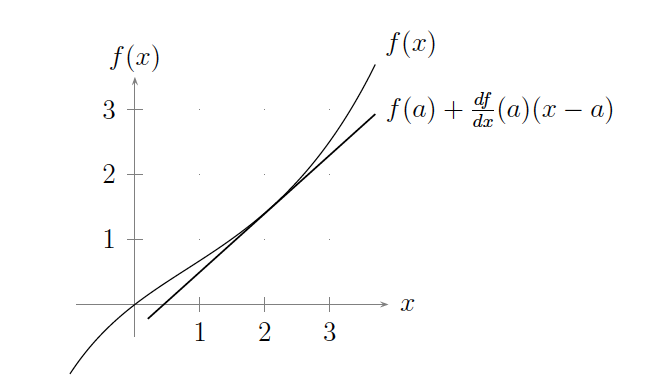Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1: Qué es el álgebra lineal

Última actualización

30 oct 2022
Guardar como PDF
- Licencias
- 1.E: Ejercicios para el Capítulo 1

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

1.1 Introducción al MAT 67

Esta clase bien puede ser una de tus primeras clases de matemáticas que cierra la brecha entre las clases de división inferior principalmente orientadas a la computación y las matemáticas abstractas que se encuentran en los cursos de matemáticas más avanzados. El objetivo de esta clase es triple:

Aprenderás Álgebra Lineal, que es una de las teorías matemáticas más utilizadas alrededor. El Álgebra Lineal encuentra aplicaciones en prácticamente todas las áreas de las matemáticas, incluyendo Cálculo Multivariado, Ecuaciones Diferenciales y Teoría de Probabilidad. También se aplica ampliamente en campos como la física, la química, la economía, la psicología y la ingeniería. Incluso estás confiando en métodos de Álgebra Lineal cada vez que usas una búsqueda en Internet como Google, el Sistema de Posicionamiento Global (GPS) o un celular.
Adquirirás habilidades computacionales para resolver sistemas lineales de ecuaciones, realizar operaciones en matrices, calcular valores propios y encontrar determinantes de matrices.
En la configuración de Álgebra Lineal, se le introducirá a la abstracción. Desarrollaremos juntos la teoría del Álgebra Lineal, y aprenderás a escribir pruebas.

Las conferencias desarrollarán principalmente la teoría del Álgebra Lineal, y las sesiones de discusión se centrarán en los aspectos computacionales. Las conferencias y las secciones de discusión van de la mano, y es importante que asistas a ambas. Los ejercicios para cada Capítulo se dividen en ejercicios más orientados a la computación y ejercicios que se centran en la escritura de pruebas. También hay algunos conjuntos de tareas de trabajo web muy cortos para asegurarse de que tenga algunas habilidades básicas. Ya puedes probar el primero que introduce algunos conceptos lógicos haciendo clic a continuación: Enlace de trabajo web.

1.2 ¿Qué es el álgebra lineal?

El Álgebra Lineal es la rama de las matemáticas cuyo objetivo es resolver sistemas de ecuaciones lineales con un número finito de incógnitas. En particular, a uno le gustaría obtener respuestas a las siguientes preguntas:

Caracterización de soluciones: ¿Existen soluciones para un determinado sistema de ecuaciones lineales? ¿Cuántas soluciones hay?
Encontrar soluciones: ¿Cómo se ve el conjunto de soluciones? ¿Cuáles son las soluciones?

El álgebra lineal es una teoría sistemática respecto a las soluciones de sistemas de ecuaciones lineales.

Ejemplo 1.2.1. Tomemos el siguiente sistema de dos ecuaciones lineales en las dos incógnitas $x_1$ y $x_2$ :

\ begin {ecuación*}\ left. \ begin {array} {rl} 2x_1 + x_2 &= 0\\ x_1 - x_2 &= 1\ end {array}\ right\}. \ end {ecuación*}

Este sistema tiene una solución única para $x_1,x_2 \in \mathbb{R}$ , a saber $x_1=\frac{1}{3}$ y $x_2=-\frac{2}{3}$ . Esta solución se puede encontrar de varias maneras diferentes. Un enfoque es resolver primero una de las incógnitas en una de las ecuaciones y luego sustituir el resultado por la otra ecuación. Aquí, por ejemplo, podríamos resolver para obtener

$x_1 = 1 + x_2$

a partir de la segunda ecuación. Entonces, sustituyendo esto en lugar de $x_1$ en la primera ecuación, tenemos

$2(1 + x_2 ) + x_2 = 0.$

A partir de esto, $x_2 = −\frac{2}{3}$ . Luego, por sustitución adicional,

$x_{1} = 1 + \left(-\frac{2}{3}\right) = \frac{1}{3}.$

Alternativamente, podemos tomar un enfoque más sistemático en la eliminación de variables. Aquí, por ejemplo, podemos restar $2$ veces la segunda ecuación de la primera ecuación para obtener $3x_2=-2$ . Es entonces inmediato eso $x_2=-\frac{2}{3}$ y, al sustituir este valor por $x_2$ en la primera ecuación, por eso $x_1=\frac{1}{3}$ .

Ejemplo 1.2.2. Tome el siguiente sistema de dos ecuaciones lineales en las dos incógnitas $x_1$ y $x_2$ :

\ begin {ecuación*}\ left. \ begin {array} {rl} x_1 + x_2 &= 1\\ 2x_1 + 2x_2 &= 1\ end {array}\ right\}. \ end {ecuación*}

Aquí, podemos eliminar variables sumando $-2$ veces la primera ecuación a la segunda ecuación, lo que resulta en $0=-1$ . Esto es obviamente una contradicción, y de ahí que este sistema de ecuaciones no tenga solución.

Ejemplo 1.2.3. Tomemos el siguiente sistema de una ecuación lineal en las dos incógnitas $x_1$ y $x_2$ :

\ begin {ecuación*} x_1 - 3x_2 = 0. \ end {ecuación*}

En este caso, hay infinitamente muchas soluciones dadas por el conjunto $\{x_2 = \frac{1}{3}x_1 \mid x_1\in \mathbb{R}\}$ . Se puede pensar en esta solución establecida como una línea en el plano euclidiano $\mathbb{R}^{2}$ :

$Screen shot 2013-12-31 a las 5.19.35 PM.png$

En general, un sistema de ecuaciones $m$ lineales en $n$ incógnitas $x_1,x_2,\ldots,x_n$ es una colección de ecuaciones de la forma

\ begin {ecuación}\ label {eq:sistema lineal}\ left. \ begin {array} {rl} a_ {11} x_1 + a_ {12} x_2 +\ cdots + a_ {1n} x_n &= b_1\\ a_ {21} x_1 + a_ {22} x_2 +\ cdots + a_ {2n} x_n &= b_2\\ vdots\ qquad &\ vdots\\ a_ {m1} x_1 + a_ {m2} x_2 +\ cdots + a_ {mn} x_n &= b_m\ end {array}\ derecha\},\ tag {1.2.1}\ end {ecuación}

donde los $a_{ij}$ s son los coeficientes (generalmente números reales o complejos) frente a las incógnitas $x_j$ , y los $b_i$ 's también son números fijos reales o complejos. Una solución es un conjunto de números $s_1,s_2,\ldots,s_n$ tal que, sustituyendo a $x_1=s_1,x_2=s_2,\ldots,x_n=s_n$ las incógnitas, se mantienen todas las ecuaciones del Sistema 1.2.1. El álgebra lineal es una teoría que se refiere a las soluciones y la estructura de soluciones para ecuaciones lineales. A medida que avance este curso, verás que hay mucha sutileza en entender completamente las soluciones para tales ecuaciones.

1.3 Sistemas de ecuaciones lineales

1.3.1 Ecuaciones lineales

Antes de continuar, reformulemos la noción de un sistema de ecuaciones lineales en el lenguaje de funciones. Esto también nos ayudará a entender un poco mejor el adjetivo ``lineal”. Una función $f$ es un mapa

\ begin {ecuación} f: X\ a Y\ tag {1.3.1}\ end {ecuación}

de un conjunto $X$ a un conjunto $Y$ . El conjunto $X$ se llama el dominio de la función, y el conjunto $Y$ se llama el espacio de destino o codominio de la función. Una ecuación es

\ begin {ecuación} f (x) =y,\ tag {1.3.2}\ end {ecuación}

dónde $x \in X$ y $y \in Y$ . (Si no está familiarizado con las nociones abstractas de conjuntos y funciones, entonces consulte el Apéndice A.)

Ejemplo 1.3.1. Deja $f:\mathbb{R}\to\mathbb{R}$ ser la función $f(x)=x^3-x$ . Entonces $f(x)=x^3-x=1$ es una ecuación. El dominio y el espacio objetivo son ambos el conjunto de números reales $\mathbb{R}$ en este caso.

En esta configuración, un sistema de ecuaciones es solo otro tipo de ecuación.

Ejemplo 1.3.2. $X=Y=\mathbb{R}^2=\mathbb{R} \times \mathbb{R}$ Sea el producto cartesiano del conjunto de números reales. Luego defina la función $f:\mathbb{R}^2 \to \mathbb{R}^2$ como

\ begin {ecuación} f (x_1, x_2) = (2x_1+x_2, x_1-x_2),\ tag {1.3.3}\ end {ecuación}

y establecer $y=(0,1)$ . Después la ecuación $f(x)=y$ , donde $x=(x_1,x_2)\in \mathbb{R}^2$ , describe el sistema de ecuaciones lineales del Ejemplo 1.2.1.

La siguiente pregunta que tenemos que responder es, ``¿ qué es una ecuación lineal?” Basándose en la definición de una ecuación, una ecuación lineal es cualquier ecuación definida por una función ``lineal” $f$ que se define en un espacio ``lineal” (también conocido como un espacio vectorial como se define en la Sección 4.1). Vamos a elaborar sobre todo esto en futuras conferencias, pero vamos a demostrar las principales características de un espacio ``lineal” en términos del ejemplo $\mathbb{R}^2$ . Tomar $x=(x_1,x_2), y=(y_1,y_2) \in \mathbb{R}^2$ . Hay dos operaciones ``lineales” definidas en $\mathbb{R}^2$ , a saber, suma y multiplicación escalar:

\ begin {align} x+y &: = (x_1+y_1, x_2+y_2) &&\ text {(adición de vectores)}\ tag {1.3.4}\\ cx &: = (cx_1, cx_2) &&\ text {(multiplicación escalar).} \ tag {1.3.5}\ end {align}

Una función ``lineal” on $\mathbb{R}^{2}$ es entonces una función $f$ que interactúa con estas operaciones de la siguiente manera:

\ begin {align} f (cx) &= cf (x)\ tag {1.3.6}\\ f (x+y) & = f (x) + f (y). \ tag {1.3.7}\ end {align}

Deberías comprobar por ti mismo que la función $f$ en el Ejemplo 1.3.2 tiene estas dos propiedades.

1.3.2 Ecuaciones no lineales

(Sistemas de) Las ecuaciones lineales son una clase muy importante de (sistemas de) ecuaciones. Aprenderás técnicas en esta clase que pueden ser utilizadas para resolver cualquier sistema de ecuaciones lineales. Las ecuaciones no lineales, por otro lado, son significativamente más difíciles de resolver. Un ejemplo es una ecuación cuadrática como

\ begin {ecuación} x^2 + x -2 =0,\ tag {1.3.8}\ end {ecuación}

que, sin razón completamente obvia, tiene exactamente dos soluciones $x=-2$ y $x=1$ . Contraste esto con la ecuación

\ begin {ecuación} x^2 + x +2 =0,\ tag {1.3.9}\ end {ecuación}

que no tiene soluciones dentro del conjunto $\mathbb{R}$ de números reales. En cambio, se tiene dos soluciones complejas $\frac{1}{2}(-1\pm i\sqrt{7}) \in \mathbb{C}$ , donde $i=\sqrt{-1}$ . (Los números complejos se discuten con más detalle en el Capítulo 2.) En general, recordemos que la ecuación cuadrática $x^2 +bx+c=0$ tiene las dos soluciones

$x = -\frac{b}{2} \pm \sqrt{\frac{b^2}{4}-c}.$

1.3.3 Transformaciones lineales

El conjunto se $\mathbb{R}^2$ puede ver como el plano euclidiano. En este contexto, las funciones lineales de la forma $f:\mathbb{R}^2 \to \mathbb{R}$ o $f:\mathbb{R}^2 \to \mathbb{R}^2$ pueden interpretarse geométricamente como ``movimientos” en el plano y se denominan transformaciones lineales.

Ejemplo 1.3.3. Recordemos el siguiente sistema lineal del Ejemplo 1.2.1:

\ begin {ecuación*}\ left. \ begin {array} {rl} 2x_1 + x_2 &= 0\\ x_1 - x_2 &= 1\ end {array}\ right\}. \ end {ecuación*}

Cada ecuación puede interpretarse como una línea recta en el plano, con soluciones $(x_1,x_2)$ al sistema lineal dadas por el conjunto de todos los puntos que se encuentran simultáneamente en ambas líneas. En este caso, las dos líneas se encuentran en una sola ubicación, lo que corresponde a la solución única al sistema lineal como se ilustra en la siguiente figura:

$Screen shot 2013-12-31 a las 5.18.36 PM.png$

Ejemplo 1.3.4. El mapa lineal

$f(x_1,x_2) = (x_1,-x_2)$ describes the ``motion'' of reflecting a vector across the

$x$ -axis, as illustrated in the following figure:

$Screen shot 2013-12-31 at 5.21.47 PM.png$

Ejemplo 1.3.5. El mapa lineal

$f(x_1,x_2) = (-x_2,x_1)$ describes the ``motion'' of rotating a vector by

$90^0$ counterclockwise, as illustrated in the following figure:

$Screen shot 2013-12-31 at 6.28.04 PM.png$

Este ejemplo puede generalizarse fácilmente a rotación por cualquier ángulo arbitrario usando Lemma 2.3.2. En particular, cuando los puntos en $\mathbb{R}^{2}$ son vistos como números complejos, entonces podemos emplear la llamada forma polar para números complejos con el fin de modelar el ``movimiento” de rotación. (Cf. Ejercicio de Prueba de Escritura 5 en Ejercicios para el Capítulo 2.)

1.3.4 Aplicaciones de ecuaciones lineales

Las ecuaciones lineales aparecen en muchos contextos diferentes. Por ejemplo, puede ver la derivada $\frac{df}{dx}(x)$ de una función diferenciable $f:\mathbb{R}\to\mathbb{R}$ como una aproximación lineal de $f$ . Esto se hace evidente cuando miras la serie Taylor de la función $f(x)$ centrada alrededor del punto $x=a$ (como se ve en un curso como MAT 21C):

\ begin {ecuación} f (x) = f (a) +\ frac {df} {dx} (a) (x-a) +\ cdots. \ tag {1.3.10}\ fin {ecuación}

En particular, podemos graficar la parte lineal de la serie Taylor versus la función original, como en la siguiente figura:

$Screen shot 2013-12-31 a las 6.29.15 PM.png$

Dado que $f(a)$ y $\frac{df}{dx}(a)$ son meramente números reales, $f(a) + \frac{df}{dx}(a) (x-a)$ es una función lineal en la única variable $x$ .

Del mismo modo, si $f:\mathbb{R}^n \to \mathbb{R}^m$ es una función multivariada, entonces todavía se puede ver la derivada de $f$ como una forma de aproximación lineal para $f$ (como se ve en un curso como MAT 21D).

¿Y si hay infinitamente muchas variables $x_1, x_2,\ldots$ ? En este caso, el sistema de ecuaciones tiene la forma

\ begin {ecuación*}\ left. \ begin {array} {rl} a_ {11} x_1 + a_ {12} x_2 +\ cdots &= y_1\\ a_ {21} x_1 + a_ {22} x_2 +\ cdots &= y_2\\\ cdots &\ end {array}\ right\}. \ end {ecuación*}

De ahí que las sumas en cada ecuación sean infinitas, y así tendríamos que lidiar con series infinitas. Esto, en particular, significa que surgen cuestiones de convergencia, donde la convergencia depende de la secuencia infinita $x=(x_1,x_2,\ldots)$ de variables. Estas preguntas no ocurrirán en este curso ya que sólo nos interesan los sistemas finitos de ecuaciones lineales en un número finito de variables. Otros temas en los que se plantean estas preguntas, sin embargo, incluyen

Ecuaciones diferenciales (como en un curso como MAT 22B o MAT 118AB);
Análisis de Fourier (como en un curso como MAT 129);
Análisis Real y Complejo (como en un curso como MAT 125AB, MAT 185AB, MAT 201ABC o MAT 202).

En cursos como MAT 150ABC y MAT 250ABC, también se ve que el Álgebra Lineal surge en el estudio de cosas como simetrías, transformaciones lineales y teoría del álgebra de mentiras.

Template:Shilling