2.2: Operaciones en números complejos

{{Template.dropdown {ruta:” /álgebra/linear_álgebra "}}}

A pesar de que hemos definido formalmente\(\mathbb{C}\) como el conjunto de todos los pares ordenados de números reales, no obstante podemos extender las operaciones aritméticas habituales\(\mathbb{R}\) para que también tengan sentido en\(\mathbb{C}\). Discutimos tales extensiones en esta sección, junto con varias otras operaciones importantes sobre números complejos.

2.2.1 Suma y resta de números complejos

La adición de números complejos se realiza por componentes, lo que significa que las partes real e imaginaria se combinan simplemente.

Definición 2.2.1. Dados dos números complejos\((x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{C}\), definimos su suma compleja para ser

\[ (x_{1}, y_{1}) + (x_{2}, y_{2}) = (x_{1} + x_{2}, y_{1} + y_{2}). \]

Ejemplo 2.2.2. \( (3, 2) + (17, -4.5) = (3 + 17, 2 - 4.5) = (20, -2.5).\)

Al igual que con los números reales, la resta se define como suma con la llamada inversa aditiva, donde la inversa aditiva de\(z=(x,y)\) se define a\(-z=(-x,-y)\).

Ejemplo 2.2.3. \( (\pi, \sqrt{2}) - (\pi/2, \sqrt{19}) = (\pi, \sqrt{2}) + (-\pi/2, -\sqrt{19}), \)

donde

\[ (\pi, \sqrt{2}) + (-\pi/2, -\sqrt{19}) = (\pi - \pi/2, \sqrt{2} - \sqrt{19}) = (\pi/2, \sqrt{2} - \sqrt{19}). \]

La adición de números complejos comparte muchas de las mismas propiedades que la adición de números reales, incluyendo la asociatividad, la conmutatividad, la existencia y singularidad de una identidad aditiva, y la existencia y singularidad de las inversas aditivas. Resumimos estas propiedades en el siguiente teorema, que debes probar para tu propia
práctica.

Teorema 2.2.4. \(z_{1}, z_{2}, z_{3} \in \mathbb{C}\)Sea cualquiera de tres números complejos. Entonces son ciertas las siguientes afirmaciones.

1. (Asociatividad)\((z_{1} + z_{2}) + z_{3} = z_{1} + (z_{2} + z_{3})\).
2. (Conmutatividad)\(z_{1} + z_{2} = z_{2} + z_{1}\).
3. (Identidad Aditiva) Existe un número complejo único, denotado\(0\), tal que, dado cualquier número complejo\(z \in \mathbb{C}\),\(0 + z = z\). Por otra parte,\(0 = (0, 0)\).
4. (Inversa Aditiva) Dado cualquier número complejo\(z \in \mathbb{C}\), existe un número complejo único, denotado\(-z\), tal que\(z + (-z) = 0\). Además, si\(z = (x, y)\) con\(x, y \in \mathbb{R}\), entonces\(-z = (-x, -y)\).

La prueba de este teorema es sencilla y se basa únicamente en la definición de adición compleja junto con las propiedades familiares de adición para números reales. Por ejemplo, para verificar la conmutatividad, dejar\(z_{1} = (x_{1}, y_{1})\) y\(z_{2} = (x_{2}, y_{2})\) ser números complejos con\(x_{1}, x_{2}, y_{1}, y_{2} \in \mathbb{R}\).
Entonces
\[
z_{1} + z_{2} =
(x_{1} + x_{2}, y_{1} + y_{2}) =
(x_{2} + x_{1}, y_{2} + y_{1}) =
z_{2} + z_{1}.
\]

2.2.2 Multiplicación y división de números complejos

La definición de multiplicación para dos números complejos es a primera vista algo menos sencilla que la de suma.

Definición 2.2.5. Dados dos números complejos\((x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{C}\), definimos que su producto complejo es

\[ (x_{1}, y_{1})(x_{2}, y_{2}) = (x_{1}x_{2} - y_{1}y_{2} , x_{1}y_{2} + x_{2}y_{1}). \]

De acuerdo con esta definición,\(i^2=-1\). En otras palabras,\(i\) es una solución de la ecuación polinómica\(z^2+1=0\), que no tiene soluciones en\(\mathbb{R}\). Resolver ecuaciones de otro modo irresolubles fue en gran parte la principal motivación detrás de la introducción de números complejos. Tenga en cuenta que la relación\(i^2=-1\) y la suposición de que los números complejos pueden multiplicarse como números reales es suficiente para llegar a la regla general para la multiplicación de números complejos:

\ begin {alinear*}
(x_ {1} + y_ {1} i) (x_ {2} + y_ {2} i)
& =
x_ {1} x_ {2} + x_ {1} y_ {2} i + x_ {2} y_ {1} i + y_ {1} y_ {2} i^ {2}
\\
& =
x_ {1}} x_ {2} + x_ {1} y_ {2} i + x_ {2} y_ {1} i - y_ {1} y_ {2}
\\
& =
x_ {1} x_ {2} - y_ {1} y_ {2} + (x_ {1} y_ {2} + x_ {2} y_ {1}) i.
\ end {alinear*}

Al igual que con la adición, las propiedades básicas de la multiplicación compleja son lo suficientemente fáciles de probar usando la definición. Resumimos estas propiedades en el siguiente teorema, que también debes probar para tu propia práctica.

Teorema 2.2.6. \(z_{1}, z_{2}, z_{3} \in \mathbb{C}\)Sea cualquiera de tres números complejos. Entonces son ciertas las siguientes afirmaciones.

1. (Asociatividad)\((z_{1}z_{2})z_{3} = z_{1}(z_{2}z_{3})\).
2. (Conmutatividad)\(z_{1}z_{2} = z_{2}z_{1}\).
3. (Identidad Multiplicativa) Hay un número complejo único, denotado\(1\), tal que, dado cualquiera\(z \in \mathbb{C}\),\(1 z = z\). Por otra parte,\(1 = (1, 0)\).
4. (Distributividad de la Multiplicación sobre la Adición)\(z_{1}(z_{2} + z_{3}) = z_{1}z_{2} + z_{1}z_{3}\).

Así como es el caso de los números reales, cualquier número complejo distinto de cero\(z\) tiene una inversa multiplicativa única, que podemos denotar por cualquiera\(z^{-1}\) o\(1/z\).

Teorema 2.2.6. (continuación).

5. (Inversa multiplicativa) Dado\(z \in \mathbb{C}\) con\(z \neq 0\), hay un número complejo único, denotado\(z^{-1}\), tal que\(z z^{-1} = 1\). Además, si\(z = (x, y)\) con\(x, y \in \mathbb{R}\), entonces

\[ z^{-1} = \left(\frac{x}{x^{2} + y^{2}}, \frac{-y}{x^{2} + y^{2}}\right). \]

Prueba.

Singularidad: Un número complejo\(w\) es una inversa de\(z\) if\(z w=1\) (por la conmutatividad de la multiplicación compleja esto es equivalente a\(w z=1\). Primero vamos a probar que si\(w\) y\(v\) son dos números complejos tales que\(z w=1\) y\(z v=1\), entonces necesariamente tenemos\(w=v\). Esto implicará entonces que cualquiera\(z\in\mathbb{C}\) puede tener como máximo una inversa. Para ver esto, partimos de\(z v=1\). Multiplicando ambos lados por\(w\), obtenemos\(w z v=w 1\). Utilizando el hecho de que\(1\) es la unidad multiplicativa, que el producto es conmutativo, y la suposición de que\(w\) es una inversa, obtenemos\(z w v=v=w\).

Existencia: Ahora asuma\(z\in\mathbb{C}\) con\(z\neq 0\), y escribe\(z=x+y i\) para\(x,y\in\mathbb{R}\). Ya que\(z\neq 0\), al menos uno de\(x\) o no\(y\) es cero, y así\(x^2 + y^2 >0\). Por lo tanto, podemos definir

\[ w=\left(\frac{x}{x^{2} + y^{2}}, \frac{-y}{x^{2} + y^{2}}\right), \]

y uno puede comprobarlo\(z w=1\).

Ahora, podemos definir la división de un número complejo\(z_1\) por un número complejo distinto de cero\(z_2\) como el producto de\(z_1\) y\(z_2^{-1}\). Explícitamente, para dos números complejos\(z_1= x_{1} + i y_{1}\) y\(z_2 =x_{2} +i y_{2}\), tenemos que su cociente complejo es

\[ \frac{z_1}{z_2} = \frac{x_{1}x_{2} + y_{1}y_{2}+ \left(x_{2}y_{1} - x_{1}y_{2}\right)i}{x_{2}^{2} + y_{2}^{2}}. \]

Ejemplo 2.2.7. Ilustramos la definición anterior con el siguiente ejemplo:
\[
\frac{(1, 2)}{(3, 4)}
=
\left(
\frac{1\cdot 3 + 2\cdot 4}{3^{2} + 4^{2}}
,
\frac{3\cdot 2 - 1\cdot 4}{3^{2} + 4^{2}}
\right)
=
\left(
\frac{3 + 8}{9 + 16}
,
\frac{6 - 4}{9 + 16}
\right)
=
\left(
\frac{11}{25}
,
\frac{2}{25}
\right).
\]

2.2.3 Conjugación compleja

La conjugación compleja es una operación sobre la\(\mathbb{C}\) que resultará muy útil porque nos permite manipular solo la parte imaginaria de un número complejo. En particular, cuando se combina con la noción de módulo (tal como se define en la siguiente sección), es una de las operaciones más fundamentales sobre\(\mathbb{C}\). La definición y las propiedades más básicas de la conjugación compleja son las siguientes. (Al igual que en las secciones anteriores, debes proporcionar una prueba del teorema a continuación para tu propia práctica.)

Definición 2.2.8. Dado un número complejo\(z = (x, y) \in \mathbb{C}\) con\(x, y \in \mathbb{R}\), definimos el conjugado (complejo) de\(z\) ser el número complejo

\[ \bar{z} = (x, -y). \]

Teorema 2.2.9. Teniendo en cuenta dos números complejos\(z_{1}, z_{2} \in \mathbb{C}\),

1. \(\overline{z_{1} + z_{2}} = \overline{z_{1}} + \overline{z_{2}}\).
2. \(\overline{z_{1}z_{2}} = \overline{z_{1}}\, \overline{z_{2}}\).
3. \( \overline{1/z_1} = 1/\overline{z_1}\), para todos\(z_1\neq 0\).
4. \(\overline{z_{1}} = z_{1}\)si y sólo si\(\ImaginaryPart(z_{1}) = 0\).
5. \(\overline{\overline{z_{1}}} = z_{1}\).
6. las partes reales e imaginarias de\(z_{1}\) pueden expresarse como

\[ \mathrm{Re}(z_{1}) = \frac{1}{2}(z_{1} + \overline{z_{1}})
{\rm \quad and \quad}
\mathrm{Im}(z_{1}) = \frac{1}{2 i}(z_1 - \overline{z_1}). \]

2.2.4 El módulo (también conocido como norma, longitud o magnitud)

En esta sección, introducimos otra operación más sobre números complejos, esta vez basada en una generalización de la noción de valor absoluto de un número real. Para motivar la definición, es útil ver el conjunto de números complejos como el plano euclídeo bidimensional, es decir, pensar en\(\mathbb{C}=\mathbb{R}^2\) ser iguales como conjuntos. El módulo, o longitud, de\(z\in\mathbb{C}\) se define entonces como la distancia euclidiana entre\(z\), como punto en el plano, y el origen\(0 = (0,0)\). Este es el contenido de la siguiente definición.

Definición 2.2.10. Dado un número complejo\(z = (x, y) \in \mathbb{C}\) con\(x, y \in \mathbb{R}\), el módulo de\(z\) se define como

\[ |z| = \sqrt{x^{2} + y^{2}}. \]

En particular, dado\(x \in \mathbb{R}\), señalar que

\[ | (x, 0) | = \sqrt{x^{2} + 0} = | x | \]

bajo la convención de que la función de raíz cuadrada adquiere su principal valor positivo.

Ejemplo 2.2.11. Usando la definición anterior, vemos que el módulo del número complejo\((3, 4)\) es

\[ | (3, 4) | = \sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5. \]

Para ver esto geométricamente, construya una figura en el plano euclidiano, como

y aplicar el teorema de Pitágoras al triángulo rectángulo resultante para encontrar la distancia desde el origen hasta el punto\((3, 4)\).

El siguiente teorema enumera las propiedades fundamentales del módulo, y especialmente en lo que se refiere a la conjugación compleja. Debes proporcionar una prueba para tu propia práctica.

Teorema 2.2.12. Teniendo en cuenta dos números complejos\(z_{1}, z_{2} \in \mathbb{C}\),

1. \(|z_{1}z_{2}| = |z_{1}|\cdot|z_{2}|\).
2. \({\displaystyle \left|\frac{z_{1}}{z_{2}}\right| = \frac{|z_{1}|}{|z_{2}|}}\), suponiendo que\(z_{2} \neq 0\).
3. \(|\overline{z_{1}}| = |z_{1}|\).
4. \(|\mathrm{Re}(z_{1})| \leq |z_{1}|\)y\(|\mathrm{Im}(z_{1})| \leq |z_{1}|\).
5. (Desigualdad del Triángulo)\(|z_{1} + z_{2}| \leq |z_{1}| + |z_{2}|\).
6. (Otro Triángulo Desigualdad)\(|z_{1} - z_{2}| \geq |\,|z_{1}| - |z_{2}|\,|\).
7. (Fórmula para la inversa multiplicativa)\(z_{1}\overline{z_{1}} = |z_{1}|^{2}\), a partir de la cual

\[ z_{1}^{-1} = \frac{\overline{z_{1}}}{|z_{1}|^{2}} \]

cuando asumimos eso\(z_{1} \neq 0\).

2.2.5 Números complejos como vectores en\(\mathbb{R}^{2}\)

Cuando los números complejos son vistos como puntos en el plano euclidiano\(\mathbb{R}^{2}\), varias de las operaciones definidas en la Sección 2.2 pueden visualizarse directamente como si fueran operaciones sobre vectores.

Para los efectos de este capítulo, pensamos en los vectores como segmentos de línea dirigidos que comienzan en el origen y terminan en un punto especificado en el plano euclidiano. Estos segmentos de línea también se pueden mover en el espacio siempre que se conserve la dirección (que llamaremos el argumento en la Sección 2.3.1 a continuación) y la longitud (también conocido como el módulo). Como tal, la distinción entre puntos en el plano y vectores es meramente una cuestión de convención siempre y cuando al menos implícitamente pensemos que cada vector ha sido traducido para que comience en el origen.

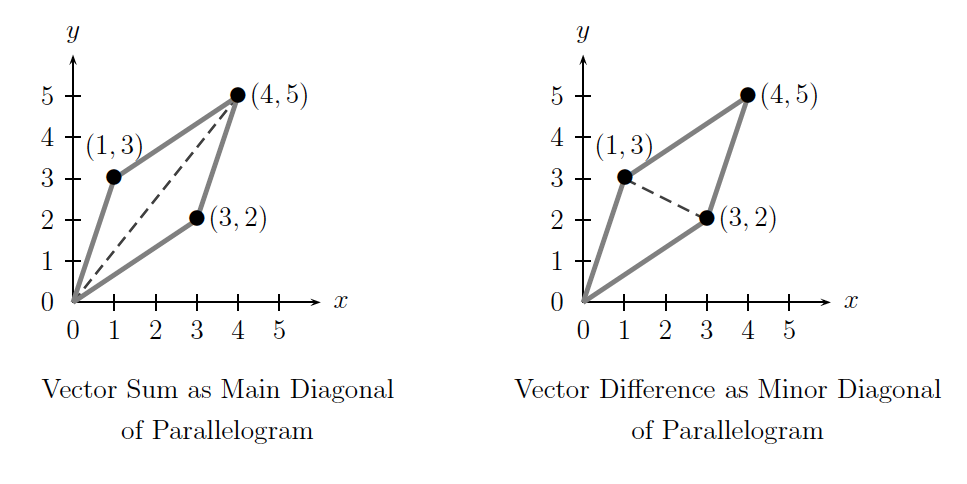
Como vimos en el Ejemplo 2.2.11 anterior, el módulo de un número complejo puede verse como la longitud de la hipotenusa de cierto triángulo rectángulo. La suma y la diferencia de dos vectores también se pueden representar geométricamente como las longitudes de diagonales específicas dentro de un paralelogramo particular que se forma copiando y traduciendo apropiadamente los dos vectores que se combinan.

Ejemplo 2.2.13. Ilustramos la suma\((3, 2) + (1, 3) = (4, 5)\) como la diagonal principal, discontinua del paralelogramo en la figura más a la izquierda a continuación. La diferencia también\((3, 2) - (1, 3) = (2, -1)\) puede verse como la diagonal más corta del mismo paralelogramo, aunque adecuadamente necesitaríamos insistir en que esta diagonal más corta se traduzca para que comience en el origen. Este último se ilustra en la figura más a la derecha a continuación.

Template:Shilling