2.3: Forma polar e interpretación geométrica

Como se mencionó anteriormente,\(\mathbb{C}\) coincide con el plano\(\mathbb{R}^{2}\) cuando se ve como un conjunto de pares ordenados de números reales. Por lo tanto, podemos usar coordenadas polares como una forma alternativa de identificar de manera única un número complejo. Esto da lugar a la llamada forma polar para un número complejo, que a menudo resulta ser una representación conveniente para números complejos.

Forma polar para números complejos

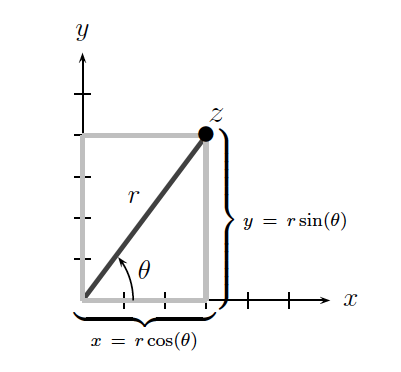
El siguiente diagrama resume las relaciones entre las coordenadas cartesianas y polares en\(\mathbb{R}^2\):

Llamamos al par ordenado\((x, y)\) las coordenadas rectangulares para el número complejo\(z\).

También llamamos al par ordenado\((r, \theta)\) las coordenadas polares para el número complejo\(z\). El radio\(r = |z|\) se llama el módulo de\(z\) (como se define en la Sección 2.2.4 anterior), y el ángulo\(\theta = \Argument(z)\) se llama el argumento de\(z\). Dado que el argumento de un número complejo describe un ángulo que se mide con relación al\(x\) eje -eje, es importante señalar que solo\(\theta\) está bien definido hasta sumar múltiplos de\(2\pi\). Como tal, restringimos\(\theta \in [0, 2\pi)\) y sumamos o restamos múltiplos de\(2\pi\) según sea necesario (por ejemplo, al multiplicar dos números complejos para que sus argumentos se sumen juntos) para mantener el argumento dentro de este rango de valores.

Es sencillo transformar coordenadas polares en coordenadas rectangulares usando las ecuaciones

\ begin {ecuación}\ label {eq:sincos}
x = r\ cos (\ theta)
{\ rm\ quad y\ quad}
y = r\ sin (\ theta). \ tag {2.3.1}
\ fin {ecuación}

Para transformar coordenadas rectangulares en coordenadas polares, primero notamos que\(r = \sqrt{x^{2} + y^{2}}\) es solo el módulo complejo. Entonces, se\(\theta\) debe elegir para que satisfaga los límites\(0 \leq \theta < 2\pi\) además de las ecuaciones simultáneas (2.3.1) donde estamos suponiendo que\(z \neq 0\).

Resumiendo:

\[ z = x + y i = r\cos(\theta) + r\sin(\theta)i = r(\cos(\theta) + \sin(\theta)i). \]

Parte de la utilidad de esta expresión es que el tamaño\(r = |z|\) de\(z\) es explícitamente parte de la definición misma ya que es fácil verificarlo\(|\cos(\theta) + \sin(\theta)i| = 1\) para cualquier elección de\(\theta \in \mathbb{R}\).

Muy relacionada está la forma exponencial para números complejos, que no hace más que reemplazar la expresión\(\cos(\theta) + \sin(\theta)i\) con\(e^{i \theta}\). El verdadero poder de esta definición es que esta notación exponencial resulta ser completamente consistente con el uso habitual de la notación exponencial para números reales.

Ejemplo\(\PageIndex{1}\):

El número complejo\(i\) en coordenadas polares se expresa como\(e^{i\pi/2}\), mientras que el número\(-1\) viene dado por\(e^{i\pi}\).

2.3.2 Multiplicación geométrica para números complejos

Como se discutió en la Sección 2.3.1 anterior, la forma exponencial general para un número complejo\(z\) es una expresión de la forma\(r e^{i \theta}\) donde\(r\) es un número real no negativo y\(\theta \in [0, 2\pi)\). La utilidad de esta notación se observa inmediatamente al multiplicar dos números complejos:

Nota

Lema 2.3.2. Let\(z_{1} = r_{1}e^{i \theta_{1}}, z_{2} = r_{2}e^{i \theta_{2}} \in \mathbb{C}\) Ser números complejos en forma exponencial. Entonces

\[ z_1 z_2 = r_1 r_2 e^{i(\theta_1+\theta_2)}. \]

Comprobante.

Por cómputo directo,

\ begin {ecuación*}
\ begin {split}
z_ {1} z_ {2} &= (r_ {1} e^ {i\ theta_ {1}}) (r_ {2} e^ {i\ theta_ {2}})
= r_ {1} r_ {2} e^ {i\ theta_ {1}} e^ {i\ theta_ eta_ {2}}\\
&= r_1 r_2 (\ cos\ theta_1 +i\ sin\ theta_1) (\ cos\ theta_2+i\ sin\ theta_2)\\
&= r_1 r_2\ bigl [ (\ cos\ theta_1\ cos\ theta_2 -\ sin\ theta_1\ sin\ theta_2)
+i (\ sin\ theta_1\ cos\ theta_2 +\ cos\ theta_1\ sin\ theta_2)\ bigr]\\
&= r_1 r_2\ bigl [\ cos (\ theta_1+\ theta_2) + i\ sin (\ theta_1+\ theta_2)\ bigr]
= r_1 r_2 e^ {i (\ theta_1+\ theta_2)},
\ end {split}
\ end {ecuación*}

donde hemos utilizado las fórmulas habituales para el seno y el coseno de la suma de dos ángulos.

\(\square\)

En particular, Lemma 2.3.2 muestra que el módulo\(|z_{1}z_{2}|\) del producto es el producto de los módulos\(r_{1}\) y\(r_{2}\) y que el argumento\(\Argument(z_{1}z_{2})\) del producto es la suma de los argumentos\(\theta_{1} + \theta_{2}\).

2.3.3 Exponenciación y extracción de raíces

Otro uso importante para la forma polar de un número complejo es en la exponenciación. La situación más simple posible aquí implica el uso de un entero positivo como potencia, en cuyo caso la exponenciación no es más que multiplicación repetida. Dadas las observaciones de la Sección 2.3.2 anterior y utilizando algunas identidades trigonométricas, se obtiene rápidamente el siguiente resultado fundamental.

Teorema 2.3.3. Dejar\(z = r(\cos(\theta) + \sin(\theta)i)\) ser un número complejo en forma polar y\(n \in \mathbb{Z}_{+}\) ser un entero positivo. Entonces

1. la exponenciación\(z^{n} = r^{n}(\cos(n\theta) + \sin(n\theta)i)\) y
2. las\(n^{\rm th}\) raíces de\(z\) están dadas por los números\(n\) complejos

\ [
z_ {k} = r^ {1/n}\ izquierda [\ cos\ izquierda (\ frac {\ theta} {n} +
\ frac {2\ pi k} {n}\ derecha) +\ sin\ izquierda (\ frac {\ theta} {n} +
\ frac {2\ pi k} {n}\ derecha) i\ derecha]
= r^ {1/n} e^ {\ frac {i} {n} (\ theta + 2\ pi k)},
\]

donde\(k = 0, 1, 2, \ldots, n - 1\).

Tenga en cuenta, en particular, que no sólo siempre se nos garantiza la existencia de una\(n^{\rm th}\) raíz para cualquier número complejo, sino que también siempre se nos garantiza tener exactamente\(n\) de ellos. Este nivel de integridad en la extracción de raíces contrasta muy bruscamente con el delicado cuidado que se debe tener cuando se desea extraer raíces de números reales sin la ayuda de números complejos.

Un importante caso especial de la Fórmula de Moivre produce una familia infinita de números bien estudiados llamados las raíces de la unidad. Por unidad, solo nos referimos al número complejo\(1 = 1 + 0i\), y por\(n^{\rm th}\) las raíces de la unidad, nos referimos a los\(n\) números

\ begin {align*}
z_ {k}
\ =\ &
1^ {1/n}\ izquierda [\ cos\ izquierda (\ frac {0} {n} +
\ frac {2\ pi k} {n}\ derecha) +\ sin\ izquierda (\ frac {0} {n} +
\ frac {2\ pi k} {n}\ derecha) i
\ derecha]
\\ = &
\ cos\ izquierda (\ frac {2\ pi
k} {n}\ derecha) +\ sin\ izquierda (\ frac {2\ pi
k} {n}\ derecha) i\\
\ =\ & e^ {2\ pi i (k/n)},
\ end {align*}
donde\(k = 0, 1, 2, \ldots, n - 1\). Estos números tienen muchas propiedades interesantes y aplicaciones importantes a pesar de lo simples que puedan parecer.

Ejemplo\(\PageIndex{4}\)

Para encontrar todas las soluciones de la ecuación\(z^3+8=0\) para\(z\in \mathbb{C}\), podemos escribir\(z=r e^{i\theta}\) en forma polar con\(r>0\) y\(\theta\in[0,2\pi)\). Entonces la ecuación\(z^3+8=0\) se vuelve\(z^3=r^3 e^{i 3\theta}=-8=8 e^{i\pi}\) así para eso\(r=2\) y\(3\theta=\pi+2\pi k\) para\(k=0,1,2\). Esto significa que hay tres soluciones distintas cuando\(\theta \in [0,2\pi)\), a saber\(\theta=\frac{\pi}{3}\),\(\theta=\pi\), y\(\theta=\frac{5\pi}{3}\).

2.3.4 Algunas funciones elementales complejas

Concluimos estas notas definiendo tres de las funciones elementales básicas que toman argumentos complejos. En este contexto, ``función elemental” se utiliza como término técnico y esencialmente significa algo así como ``una de las formas más comunes de funciones que se encuentran al comenzar a aprender Cálculo”. Las funciones elementales más básicas incluyen las funciones polinomiales y algebraicas familiares, como la función\(n^{\rm th}\) raíz, además de la función exponencial algo más sofisticada, las funciones trigonométricas y la función logarítmica. A los efectos de estas notas, definiremos ahora la función exponencial compleja y dos funciones trigonométricas complejas. Las definiciones para las funciones elementales básicas restantes se pueden encontrar en cualquier libro sobre Análisis Complejo.

Las bases básicas para definir la función exponencial compleja ya se pusieron en marcha en las Secciones 2.3.1 y 2.3.2 anteriores. En particular, ya hemos definido la expresión\(e^{i\theta}\) para significar la suma\(\cos(\theta) + \sin(\theta)i\) para cualquier número real\(\theta\). Históricamente, esta equivalencia es un caso especial de la fórmula más general de Euler:

\[ e^{x + y i} = e^{x}(\cos(y) + \sin(y)i), \]

que aquí tomamos como nuestra definición de la función exponencial compleja aplicada a cualquier número complejo\(x + y i\) para\(x, y \in \mathbb{R}\).

Dada esta función exponencial, se puede definir la función sinusoidal compleja y la función coseno compleja como

\[ \sin(z) = \frac{e^{i z} - e^{-i z}}{2 i} {\rm \quad and \quad} \cos(z) = \frac{e^{i z} + e^{-i z}}{2}.\]

Notablemente, estas funciones conservan muchas de sus propiedades familiares, las cuales deben tomarse como una señal de que las definiciones, por más abstractas que sean, han sido bien pensadas. Resumimos algunas de estas propiedades de la siguiente manera.

Teorema 2.3.5

Dado\(z_{1}, z_{2} \in \mathbb{C}\),

1. \(e^{z_{1} + z_{2}} = e^{z_{1}} e^{z_{2}}\)y\(e^{z} \neq 0 \) para cualquier elección de\(z \in \mathbb{C}\).
2. \(\sin^{2}(z_{1}) + \cos^{2}(z_{1}) = 1\).
3. \(\sin(z_{1} + z_{2}) = \sin(z_{1})\cdot\cos(z_{2}) + \cos(z_{1})\cdot\sin(z_{2})\).
4. \(\cos(z_{1} + z_{2}) = \cos(z_{1})\cdot\cos(z_{2}) - \sin(z_{1})\cdot\sin(z_{2})\).

Template:Shilling