1.1: Fibras nerviosas y el Cuarteto Strang
- Page ID
- 113126
Deseamos confirmar, con el ejemplo, la afirmación prefatoria de que el álgebra matricial es un medio útil para organizar (exponer y resolver) problemas multivariables. En nuestro primer ejemplo de este tipo investigamos la respuesta de una fibra nerviosa a un estímulo de corriente constante. Idealmente, una fibra nerviosa es simplemente un cilindro de radio aa y longitud\(l\) que conduce electricidad tanto a lo largo de su longitud como a través de su membrana lateral. Aunque en capítulos posteriores profundizaremos en la biofísica, aquí, en nuestra primera salida, nos apegaremos a sus propiedades puramente resistivas. Estos últimos se expresan a través de dos cantidades:
- \(\rho_{i}\)la resistividad en\(\Omega cm\) el citoplasma que llena la célula, y
- \(\rho_{m}\)la resistividad en\(\Omega cm^{2}\) la membrana lateral de la célula.
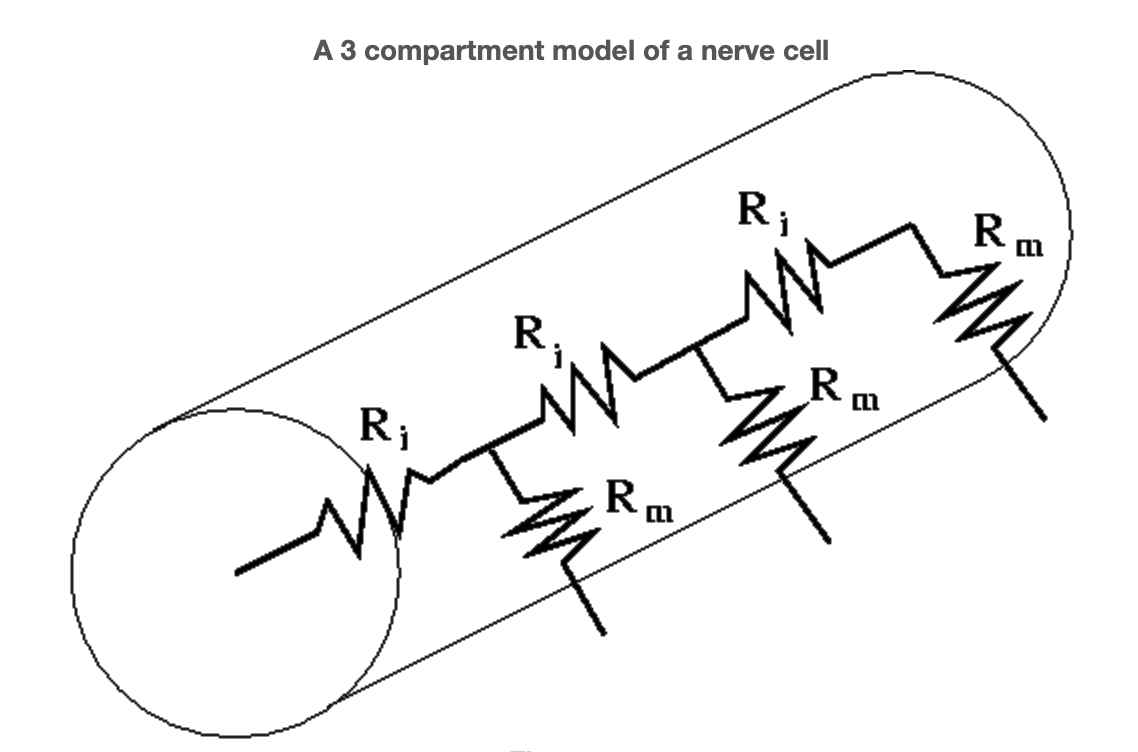
Aunque la corriente seguramente varía de punto a punto a lo largo de la fibra, se espera que estas variaciones sean lo suficientemente regulares como para ser capturadas por un modelo multicompartimental. Con eso queremos decir que elegimos un número\(N\) y dividimos la fibra en\(N\) segmentos cada uno de longitud\(\frac{l}{N}\) Denotando la resistencia axial de un segmento
\[R_{i} = \frac{\rho_{i} \frac{l}{N}}{\pi a^2} \nonumber\]
y resistencia de membrana
\[R_{m} = \frac{\rho_{m}}{2\pi a \frac{l}{N}} \nonumber\]
llegamos al modelo de circuito agrupado de la Figura 1. Para una fibra en cultivo podemos asumir un potencial extracelular constante, por ejemplo, cero. Lo logramos conectando y poniendo a tierra los nodos extracelulares, ver Figura 2.
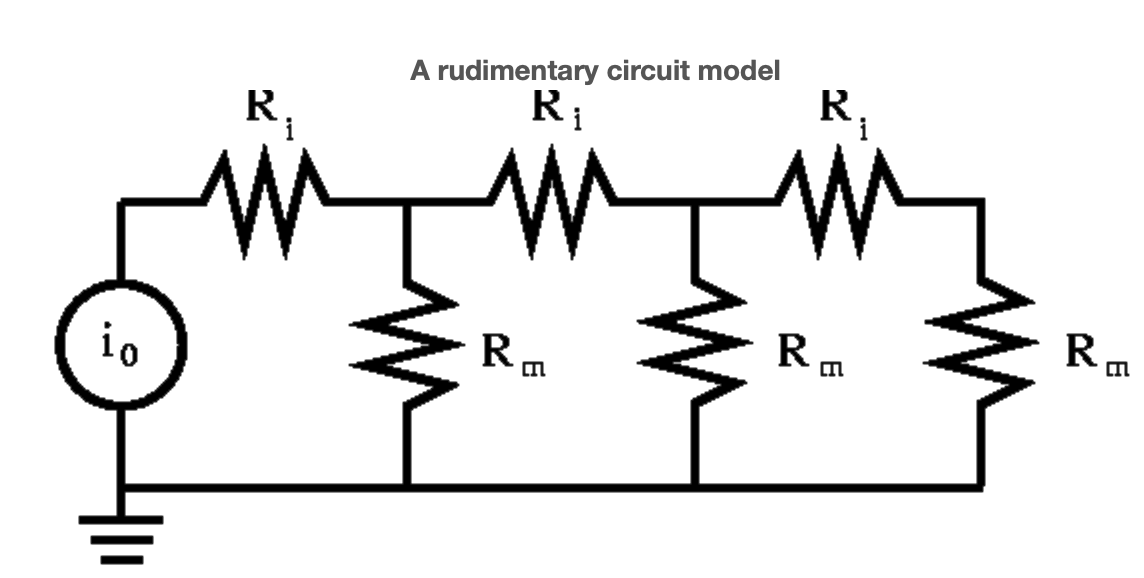
La Figura 2 también incorpora la perturbación exógena, un estímulo de corriente entre tierra y el extremo izquierdo de la fibra. Nuestro objetivo inmediato es calcular las corrientes resultantes a través de cada resistor y el potencial en cada uno de los nodos. Nuestro objetivo a largo plazo es proporcionar una metodología de modelado que se pueda utilizar en todas las disciplinas de ingeniería y ciencias. Como ayuda para computar las cantidades deseadas les damos nombres. Con respecto a la figura 3, etiquetamos el vector de potenciales
\[x = \begin{pmatrix} {x_{1}}&{x_{2}}&{x_{3}}&{x_{4}} \end{pmatrix} \nonumber\]
\[y = \begin{pmatrix} {y_{1}}&{y_{2}}&{y_{3}}&{y_{4}}&{y_{5}}&{y_{6}} \end{pmatrix} \nonumber\]
También hemos asignado (arbitrariamente) direcciones a las corrientes como ayuda gráfica en la aplicación consistente de las leyes básicas de circuitos.
Incorporamos las leyes de circuito en una metodología de modelado que toma la forma de un Cuarteto Strang:
- (S1) Expresar las caídas de voltaje a través de\(\textbf{e} = -(A \textbf{x})\)
- (S2) Ley de Express Ohm vía\(\textbf{y} = G \textbf{e}\)
- (S3) Expresar la Ley Actual de Kirchhoff vía\(A^{T} \textbf{y} = -\textbf{f}\)
- (S4) Combine lo anterior en\(A^{T}GA \textbf{x} = \textbf{f}\)
El\(A\) in (S1) es la matriz de adyacencia de borde de nodo: codifica la conectividad de la red. El\(G\) in (S2) es la matriz diagonal de conductancias de borde — codifica la física de la red. El\(\textbf{f}\) in (S3) es el vector de fuentes de corriente — codifica los estímulos de la red. El culminante\(A^{T}GA\) en (S4) es la matriz simétrica cuya inversa, cuando se aplica a\(\textbf{f}\), revela el vector de potenciales,\(\textbf{x}\). Para hacer nuestras estas ideas debemos trabajar muchos, muchos ejemplos.
Cuarteto Strang, Paso 1
Con respecto al circuito de la Figura 3, de acuerdo con el paso 1, expresamos las seis diferencias de potencial (siempre cola menos cabeza)
\[e_{1} = x_{1}-x_{2} \nonumber\]
\[e_{2} = x_{2} \nonumber\]
\[e_{3} = x_{2}-x_{3} \nonumber\]
\[e_{4} = x_{3} \nonumber\]
\[e_{5} = x_{3}-x_{4} \nonumber\]
\[e_{6} = x_{4} \nonumber\]
Listas tan largas y tediosas claman por la representación matricial, a saber\( \textbf{e} = -(A \textbf{x})\) dónde
\[A = \begin{pmatrix} {-1}&{1}&{0}&{0}\\ {0}&{-1}&{0}&{0}\\ {0}&{-1}&{1}&{0}\\ {0}&{0}&{-1}&{0}\\ {0}&{0}&{-1}&{1}\\ {0}&{0}&{0}&{-1}\\ \end{pmatrix} \nonumber\]
Cuarteto Strang, Paso 2
El paso 2, Ley de Ohm, establece:
La corriente a lo largo de un borde es igual a la caída potencial a través del borde dividida por la resistencia del borde.
En nuestro caso,
\[\begin{array}{ccccc} {y_{j} = \frac{e_{j}}{R_{i}},}&{j = 1, 3, 5}&{and}&{y_{j} = \frac{e_{j}}{R_{m}},}&{j = 2, 4, 6} \nonumber \end{array}\]
o, en notación matricial,\(\textbf{y} = G \textbf{e}\) donde
\[A = \begin{pmatrix} {\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}\\ {0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}&{0}\\ {0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}\\ {0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}\\ {0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}\\ {0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}\\ \end{pmatrix} \nonumber\]
Cuarteto Strang, Paso 3
El paso 3, Ley Actual de Kirchhoff, establece:
La suma de las corrientes en cada nodo debe ser cero.
En nuestro caso
\[i_{0}-y_{1}=0 \nonumber\]
\[y_{1}-y_{2}-y_{3} = 0 \nonumber\]
\[y_{3}-y_{4}-y_{5} = 0 \nonumber\]
\[y_{5}-y_{6} = 0 \nonumber\]
o, en términos matriciales
\[B \textbf{y} = -\textbf{f} \nonumber\]
donde
\[\begin{array}{ccc} {B = \begin{pmatrix} {-1}&{0}&{0}&{0}&{0}&{0}\\ {1}&{-1}&{-1}&{0}&{0}&{0}\\ {0}&{0}&{1}&{-1}&{-1}&{0}\\ {0}&{0}&{0}&{0}&{1}&{-1}\\ \end{pmatrix}}&{and}&{f = \begin{pmatrix} {i_{0}}\\ {0}\\ {0}\\ {0} \end{pmatrix}} \nonumber \end{array}\]
Cuarteto Strang, Paso 4
Mirando hacia atrás en A
\[A = \begin{pmatrix} {-1}&{1}&{0}&{0}\\ {0}&{-1}&{0}&{0}\\ {0}&{-1}&{1}&{0}\\ {0}&{0}&{-1}&{0}\\ {0}&{0}&{-1}&{1}\\ {0}&{0}&{0}&{-1}\\ \end{pmatrix} \nonumber\]
reconocemos en B la transposición de A
- (S1)\(\textbf{e} = -(A \textbf{x})\)
- (S2)\(\textbf{y} = G \textbf{e}\)
- (S3)\(A^{T} \textbf{y} = -\textbf{f}\)
Al sustituir los dos primeros por el tercero llegamos, de acuerdo con (S4), a
\(A^{T}GA \textbf{x} = \textbf{f}\)
Se trata de un sistema de cuatro ecuaciones para los 4 potenciales desconocidos,\(x_{1}\) a través de\(x_{4}\) Como ustedes saben, la Ecuación del sistema puede tener ya sea 1, 0, o infinitamente muchas soluciones, dependiendo de\(\textbf{f}\) y\(A^{T}GA\) nos dedicaremos (FIXME CNXN AL CAPÍTULO 3 Y 4) a un desentrañamiento de la oración anterior. Por ahora, cruzamos los dedos y 'resolvemos' invocando el programa Matlab
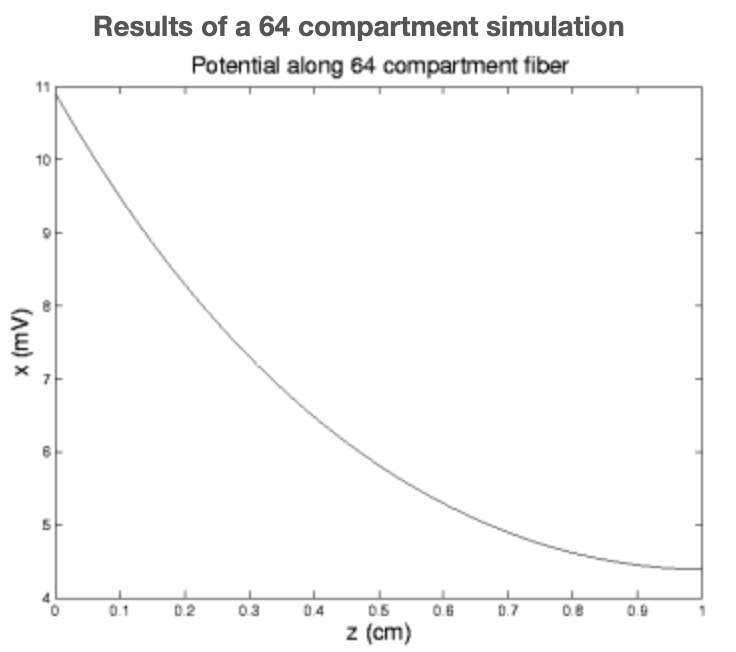
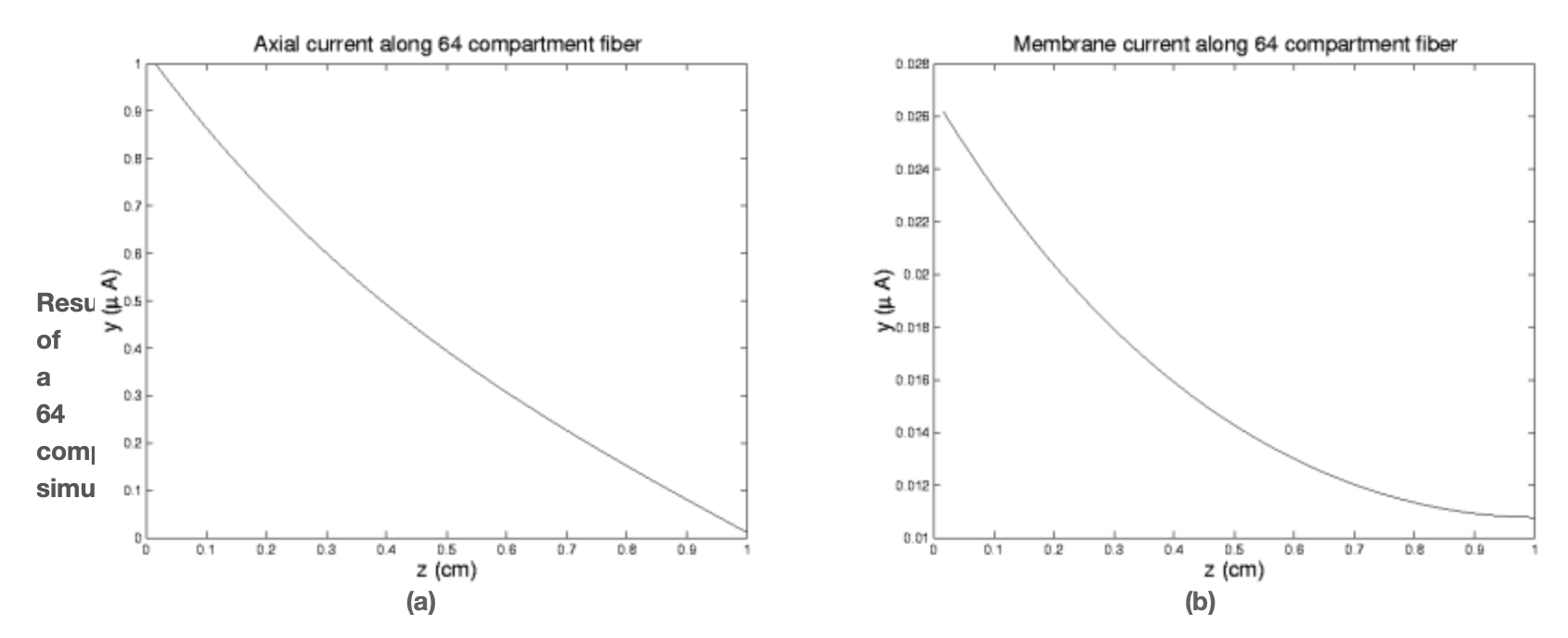
Figura 5.
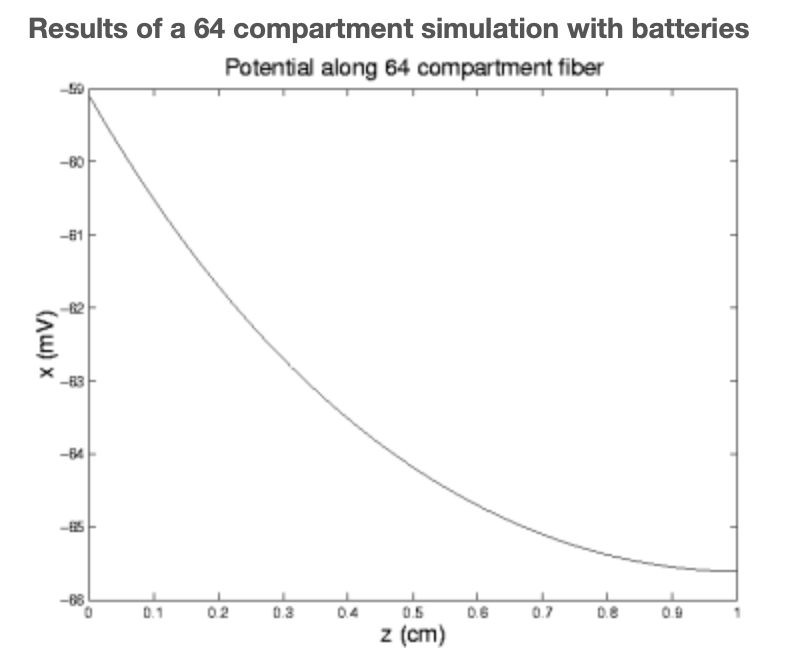
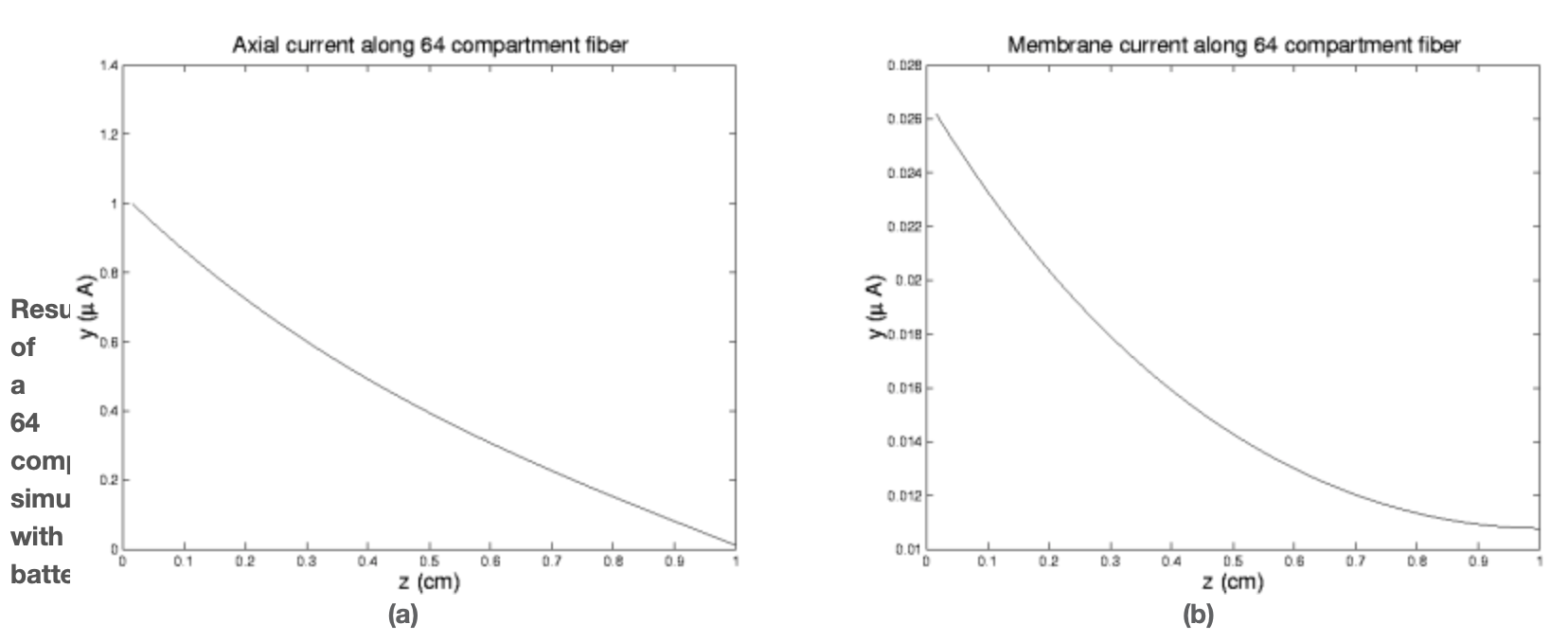
Este programa es un poco más ambicioso que lo anterior ya que nos permite especificar el número de compartimentos y que en lugar de simplemente arrojar los valores x e y los traza en función de la distancia a lo largo de la fibra. Observamos que, como era de esperar, todo se estrecha con la distancia de la fuente y que la corriente axial es significativamente mayor que la corriente de membrana, o fuga, corriente.
Hemos visto en el ejemplo anterior cómo una fuente de corriente puede producir una diferencia de potencial a través de la membrana de una célula. Observamos que, incluso en ausencia de estímulos eléctricos, siempre hay una diferencia de potencial entre el interior y el exterior de una célula viva. De hecho, esta diferencia es la definición del biólogo de 'vivir'. La vida se mantiene por el hecho de que el interior de la célula es rico en iones de potasio,\(K^{+}\) y pobre en iones de sodio,\(Na^{+}\) mientras que en el medio exterior es justo lo contrario. Estas diferencias de concentración engendran diferencias de potencial bajo la apariencia de los potenciales Nernst:
- Potenciales Nernst
\[\begin{array}{ccc} {E_{Na} = \frac{RT}{F} \log \frac{[Na]_{o}}{[Na]_{i}}}&{and}&{E_{K} = \frac{RT}{F} \log \frac{[K]_{o}}{[K]_{i}}} \nonumber \end{array}\]
donde R es la constante del gas, T es la temperatura y F es la constante de Faraday.Asociadas a estos potenciales están las resistencias de membrana
\[\begin{array}{ccc} {\rho_{m, Na}}&{and}&{\rho_{m,K}} \nonumber \end{array}\]
que en conjunto producen lo\(\rho_{m}\) anterior [1]vía
\[\frac{1}{\rho_{m}} = \frac{1}{\rho_{m, Na}}+\frac{1}{\rho_{m,K}} \nonumber\]
y producir el potencial de descanso antes mencionado
\[E_{m} = \rho_{m}(\frac{E_{Na}}{\rho_{m, Na}}+\frac{E_{K}}{\rho_{m,K}} \nonumber\]
Con respecto a nuestro antiguo modelo de circuito, cada compartimento ahora luce una batería en serie con su resistencia de membrana, como se muestra en la Figura 6.
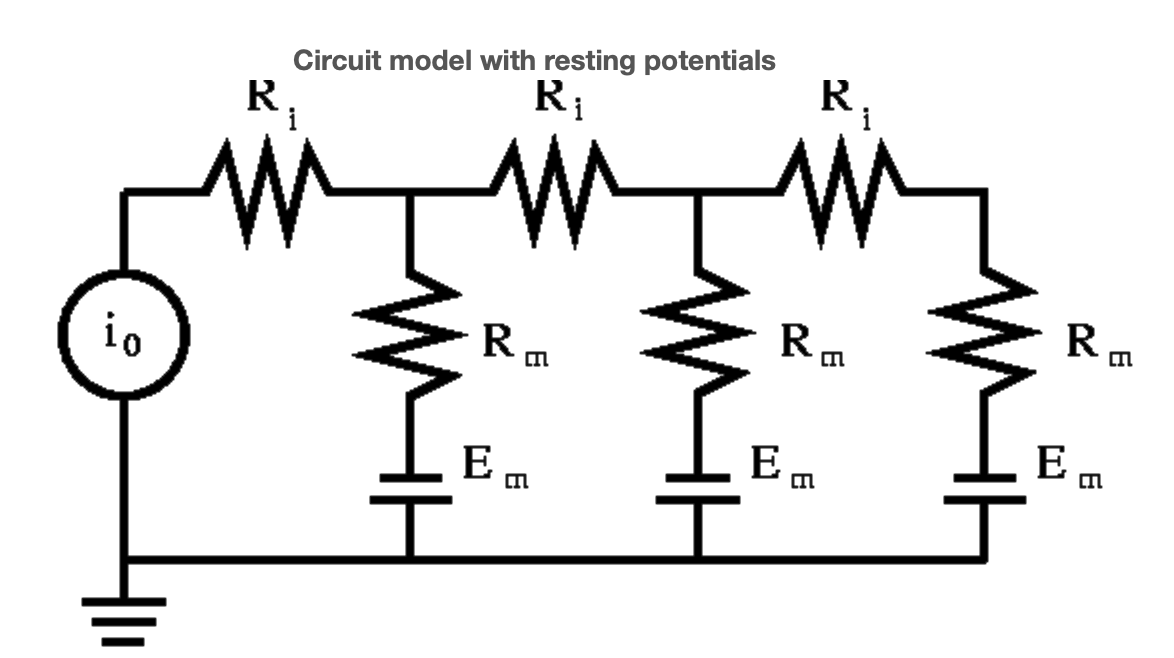
Revisando el paso (S1-4) observamos que en (S1) las caídas de voltaje pares son ahora
\[e_{2} = x_{2}-E_{m} \nonumber\]
\[e_{4} = x_{3}-E_{m} \nonumber\]
\[e_{6} = x_{4}-E_{m} \nonumber\]
Acomodamos tales cosas generalizando (S1) a:
- (S1') Exprese las caídas de voltaje como\(e = \textbf{b}-A \textbf{x}\) donde\(\textbf{b}\) está el vector de las baterías.
No son necesarios cambios para (S2) y (S3). El paso final ahora dice:
- (S4') Combinar (S1'), (S2) y (S3) para producir\(A^{T}GA \textbf{x} = A^{T}G \textbf{b} \textbf{f}\)
Volviendo a la Figura 6, observamos que
\[\begin{array}{ccc} {\textbf{b} = -\begin{pmatrix} E_{m} \begin{pmatrix} {0}\\ {1}\\ {0}\\ {1}\\ {0}\\ {1} \end{pmatrix} \end{pmatrix}}&{and}&{A^{T}G \textbf{b} = \frac{E_{m}}{R_{m}} \begin{pmatrix} {0}\\ {1}\\ {1}\\ {1} \end{pmatrix}} \nonumber \end{array}\]
Esto requiere solo cambios menores en nuestro código antiguo. Los resultados de su uso se indican en las dos cifras siguientes.