2.1: Un braguero uniaxial

Introducción

Ahora investigamos la prospección mecánica de tejido, una aplicación extensiva de técnicas desarrolladas en el análisis eléctrico de una célula nerviosa. En esta aplicación, se aplica tracción a los bordes de una muestra cuadrada de tejido plano y se busca identificar, a partir de la medición de la deformación resultante, regiones de mayor 'dureza' o 'rigidez'.

Figura\(\PageIndex{1}\): Un braguero uniaxial

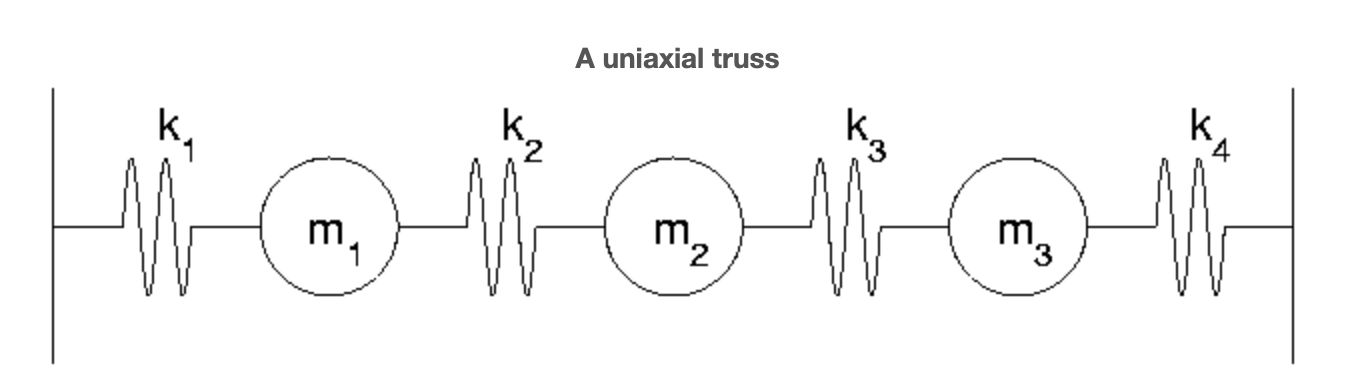
Como precursor del problema biaxial, primero consideremos el caso uniaxial. Conectamos 3 masas con cuatro resortes entre dos paredes inmóviles, aplicamos fuerzas en las masas y medimos el desplazamiento asociado. Más precisamente, suponemos que una fuerza horizontal,\(f_{j}\) se aplica a cada uno\(m_{j}\) y produce un desplazamiento\(x_{j}\) con la convención de signo que hacia la derecha significa positivo. Las barras en los extremos de la figura indican soportes rígidos incapaces de movimiento. Los\(k_{j}\) denotan las respectivas rigideces de resorte. El análogo de diferencia de potencial (ver el modelo eléctrico) es aquí elongación. Si\(e_{j}\) denota el alargamiento del resorte j entonces naturalmente,

\[e_{1} = x_{1} \nonumber\]

\[e_{2} = x_{2}-x_{1} \nonumber\]

\[e_{3} = x_{3}-x_{2} \nonumber\]

\[e_{4} = -x_{3} \nonumber\]

o, en términos matriciales,\(\textbf{e} = A⁢ \textbf{x}\) donde

\[A = \begin{pmatrix} {1}&{0}&{0}\\ {-1}&{1}&{0}\\ {0}&{-1}&{1}\\ {0}&{0}&{-1}\\ \end{pmatrix} \nonumber\]

Observamos que\(e_{j}\) es positivo cuando se estira el resorte y negativo cuando se comprime. Esta observación, la Ley de Hooke, es el análogo de la Ley de Ohm en el modelo eléctrico.

Ley de Hooke

La fuerza restauradora en un resorte es proporcional a su elongación. Llamamos a la constante de proporcionalidad la rigidez,\(k_{j}\) del resorte, y denotamos la fuerza restauradora por\(y_{j}\). La expresión matemática de esta afirmación es:\(y_{j} = k_{j} e_{j}\) en términos matriciales:\(\textbf{y} = K \textbf{⁢e}\) donde

\[K = \begin{pmatrix} {k_{1}}&{0}&{0}&{0}\\ {0}&{k_{2}}&{0}&{0}\\ {0}&{0}&{k_{3}}&{0}\\ {0}&{0}&{0}&{k_{4}}\\ \end{pmatrix} \nonumber\]

El análogo de la Ley Actual de Kirchhoff se llama aquí típicamente 'equilibrio de fuerzas'.

Equilibrio de Fuerza

El equilibrio es sinónimo de que la fuerza neta que actúa sobre cada masa debe desaparecer. En símbolos,

\[y_{1}-y_{2}-f_{1} = 0 \nonumber\]

\[y_{2}-y_{3}-f_{2} = 0 \nonumber\]

\[y_{3}-y_{4}-f_{3} = 0 \nonumber\]

o, en términos matriciales,\(B \textbf{y} = \textbf{f}\) donde

\[\begin{array}{ccc} {\textbf{f} = \begin{pmatrix} {f_{1}}\\ {f_{2}}\\ {f_{3}} \end{pmatrix}}&{and}&{\begin{pmatrix} {1}&{-1}&{0}&{0}\\ {0}&{1}&{-1}&{0}\\ {0}&{0}&{1}&{-1} \end{pmatrix}} \nonumber \end{array}\]

Como en el ejemplo eléctrico reconocemos en\(B\) la transposición de\(A\)

\[\textbf{e} = A \textbf{⁢x} \nonumber\]

\[\textbf{y} = K \textbf{⁢e} \nonumber\]

\[A^{T} \textbf{y} = \textbf{f} \nonumber\]

llegamos, vía sustitución directa, a una ecuación para\(\textbf{x}\). A saber,

\[(A^{T} \textbf{y} = \textbf{f}) \Rightarrow (A^{T}K \textbf{e} = \textbf{f}) \Rightarrow (A^{T}KA \textbf{x} = \textbf{f}) \nonumber\]

Ensamblando\(A^{T}KA \textbf{x}\) llegamos al sistema final:

\[\begin{pmatrix} {k_{1}+k_{2}}&{-k_{2}}&{0}\\ {-k_{2}}&{k_{2}+k_{3}}&{-k_{3}}\\ {0}&{-k_{3}}&{k_{3}+k_{4}} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}}\\ {x_{3}} \end{pmatrix} = \begin{pmatrix} {f_{1}}\\ {f_{2}}\\ {f_{3}} \end{pmatrix} \nonumber\]

Eliminación Gaussiana y el Truss Uniaxial

Aunque Matlab resuelve sistemas como el anterior con facilidad, nuestro objetivo aquí es desarrollar una comprensión más profunda de la Eliminación Gaussiana y así procedemos a mano. Este objetivo está motivado por una serie de consideraciones importantes. Primero, no todos los sistemas lineales tienen soluciones e incluso aquellos que no necesariamente poseen soluciones únicas. Una mirada cuidadosa a la Eliminación Gaussiana proporcionará el marco general no solo para clasificar aquellos sistemas que poseen soluciones únicas sino también para proporcionar diagnósticos detallados de aquellos sistemas defectuosos que carecen de soluciones o poseen demasiadas.

En Eliminación Gaussiana, primero se utilizan combinaciones lineales de filas anteriores para eliminar los nonceros por debajo de la diagonal principal y luego se resuelve el sistema triangular resultante a través de la sustitución inversa. Para reafirmar nuestro entendimiento, retomemos el caso donde cada una\(k_{j} = 1\) y así Ecuación toma la forma

\[\begin{pmatrix} {2}&{-1}&{0}\\ {-1}&{2}&{-1}\\ {0}&{-1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}}\\ {x_{3}} \end{pmatrix} = \begin{pmatrix} {f_{1}}\\ {f_{2}}\\ {f_{3}} \end{pmatrix} \nonumber\]

Eliminamos el elemento\((2, 1)\) (fila 2, columna 1) implementando

nueva fila 2 = fila vieja 2+\(\frac{1}{2}\) fila 1

trayendo

\[\begin{pmatrix} {2}&{-1}&{0}\\ {0}&{\frac{3}{2}}&{-1}\\ {0}&{-1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}}\\ {x_{3}} \end{pmatrix} = \begin{pmatrix} {f_{1}}\\ {f_{2}+\frac{f_{1}}{2}}\\ {f_{3}} \end{pmatrix} \nonumber\]

Eliminamos el\((3, 2)\) elemento actual implementando

nueva fila 3=fila antigua 3+\(\frac{2}{3}\) fila 2

trayendo el sistema triangular superior

\[\begin{pmatrix} {2}&{-1}&{0}\\ {0}&{\frac{3}{2}}&{-1}\\ {0}&{0}&{\frac{4}{3}} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}}\\ {x_{3}} \end{pmatrix} = \begin{pmatrix} {f_{1}}\\ {f_{2}+\frac{f_{1}}{2}}\\ {f_{3}+\frac{2f_{4}}{3}+\frac{f_{1}}{3}} \end{pmatrix} \nonumber\]

Uno ahora simplemente lee

\[x_{3} = \frac{f_{1}+2f_{2}+3f_{3}}{4} \nonumber\]

Esto a su vez permite la solución de la segunda ecuación

\[x_{2} = \frac{2(x_{3}+f_{2}+\frac{f_{1}}{2})}{3} = \frac{f_{1}+2f_{2}+f_{3}}{2} \nonumber\]

y, a su vez,

\[x_{1} = \frac{x_{2}+f_{1}}{2} = \frac{3f_{1}+2f_{2}+f_{3}}{4} \nonumber\]

Hay que decir que la Eliminación Gaussiana ha tenido éxito aquí. Porque, independientemente de los elementos reales de\(\textbf{f}\), hemos producido un\(\textbf{x}\) para el cual\(A^{T}KA \textbf{x} = \textbf{f}\).

Rutas alternativas a una solución

Si bien la Eliminación Gaussiana sigue siendo el medio más eficiente para resolver sistemas de la forma\(S \textbf{⁢x} = \textbf{f}\) que paga, en ocasiones, considerar medios alternos. A nivel algebraico, supongamos que existe una matriz que\ deshace\ multiplicación por SS en el sentido de que multiplicación por\(2^{-1}\) deshace multiplicación por 2. El análogo de matriz de\(2^{-1} 2 = 1\) es

\[S^{-1}S = I \nonumber\]

donde\(I\) denota la matriz de identidad (todos los ceros excepto los de la diagonal). Nos referimos\(S^{-1}\) como:

Inverso de S

También apodado “S inverso” para abreviar, el valor de esta matriz proviene de ver lo que sucede cuando se aplica a cada lado de\(S \textbf{⁢x} = \textbf{f}\). A saber,

\[(S \textbf{x} = \textbf{f}) \Rightarrow (S^{-1}S \textbf{x} = S^{-1} \textbf{f}) \Rightarrow (I \textbf{x} = S^{-1} \textbf{f}) \Rightarrow (\textbf{x} = S^{-1} \textbf{f}) \nonumber\]

De ahí\(\textbf{x}\) que\(S \textbf{⁢x} = \textbf{f}\) para resolver basta multiplicar\(\textbf{f}\) por la inversa de\(S\)

Método Gauss-Jordan: computar el inverso de una matriz

Consideremos ahora cómo se hace en la computación\(S^{-1}\) En general esto lleva un poco más del doble del trabajo de Eliminación Gaussiana, pues interpretamos

\[S^{-1} S = I \nonumber\]

como n (el tamaño de S\(\textbf{f}\) corriendo a través de nn columnas de la matriz de identidad. La agrupación de estas aplicaciones nn en una sola se conoce como el método Gauss-Jordan. Demostrémoslo sobre la S que aparece en la Ecuación. Primero aumentamos S con I

\[\begin{pmatrix} {2}&{-1}&{0}&{1}&{0}&{0}\\ {-1}&{2}&{-1}&{0}&{1}&{0}\\ {0}&{-1}&{2}&{0}&{0}&{1} \end{pmatrix} \nonumber\]

Luego eliminamos abajo, teniendo cuidado de abordar cada uno de los tres\(\textbf{f}\) vectores. Esto produce

\[\begin{pmatrix} {2}&{-1}&{0}&{1}&{0}&{0}\\ {0}&{\frac{3}{2}}&{-1}&{\frac{1}{2}}&{0}&{0}\\ {0}&{0}&{\frac{4}{3}}&{\frac{1}{3}}&{\frac{2}{3}}&{1} \end{pmatrix} \nonumber\]

Ahora, en lugar de una simple sustitución inversa, eliminamos. Eliminando primero el\((2, 3)\) elemento que encontramos

\[\begin{pmatrix} {2}&{-1}&{0}&{1}&{0}&{0}\\ {0}&{\frac{3}{2}}&{0}&{\frac{3}{4}}&{\frac{3}{2}}&{\frac{3}{4}}\\ {0}&{0}&{\frac{4}{3}}&{\frac{1}{3}}&{\frac{2}{3}}&{1} \end{pmatrix} \nonumber\]

En el paso final escalamos cada fila para que la matriz de la izquierda tome la forma de la identidad. Esto requiere que multiplicemos la fila 1 por\(\frac{1}{2}\) la fila 2 por\(\frac{3}{2}\) y la fila 3 por\(\frac{3}{4}\) con el resultado

\[\begin{pmatrix} {1}&{0}&{0}&{\frac{3}{4}}&{\frac{1}{2}}&{\frac{1}{4}}\\ {0}&{1}&{0}&{\frac{1}{2}}&{1}&{\frac{1}{2}}\\ {0}&{0}&{1}&{\frac{1}{4}}&{\frac{1}{2}}&{\frac{3}{4}} \end{pmatrix} \nonumber\]

Ahora en esta transformación de S en I tenemos, ipso facto, transformado I a\(S^{-1}\) i.e., la matriz que aparece a la derecha después de aplicar el método de Gauss-Jordan es la inversa de la matriz que comenzó por la izquierda. En este caso,

\[S^{-1} = \begin{pmatrix} {\frac{3}{4}}&{\frac{1}{2}}&{\frac{1}{4}}\\ {\frac{1}{2}}&{1}&{\frac{1}{2}}\\ {\frac{1}{4}}&{\frac{1}{2}}&{\frac{3}{4}} \end{pmatrix} \nonumber\]

Se debe comprobar que\(S^{-1}⁢ \textbf{f}\) efectivamente coincide con lo\(\textbf{x}\) calculado anteriormente.

Invertibilidad

No todas las matrices poseen inversas:

matriz singular

Una matriz que no tiene una inversa.

Ejemplo

Un ejemplo sencillo es:

\[\begin{pmatrix} {1}&{1}\\ {1}&{1} \end{pmatrix} \nonumber\]

Como alternativa, hay

Matrices invertibles o no singulares

Matrices que sí tienen una inversa.

Ejemplo

La matriz S que acabamos de estudiar es invertible. Otro ejemplo sencillo es

\[\begin{pmatrix} {0}&{1}\\ {1}&{1} \end{pmatrix} \nonumber\]