2.2: Una braga plana pequeña

Volvemos una vez más al problema de pruebas biaxiales, introducido en el módulo de truss uniaxial. Resulta que las matrices singulares son típicas en el problema de las pruebas biaxiales. Como nuestro primer paso en el mundo de tales estructuras planas, consideremos el truss simple en la figura de un simple swing.

Figura 1.

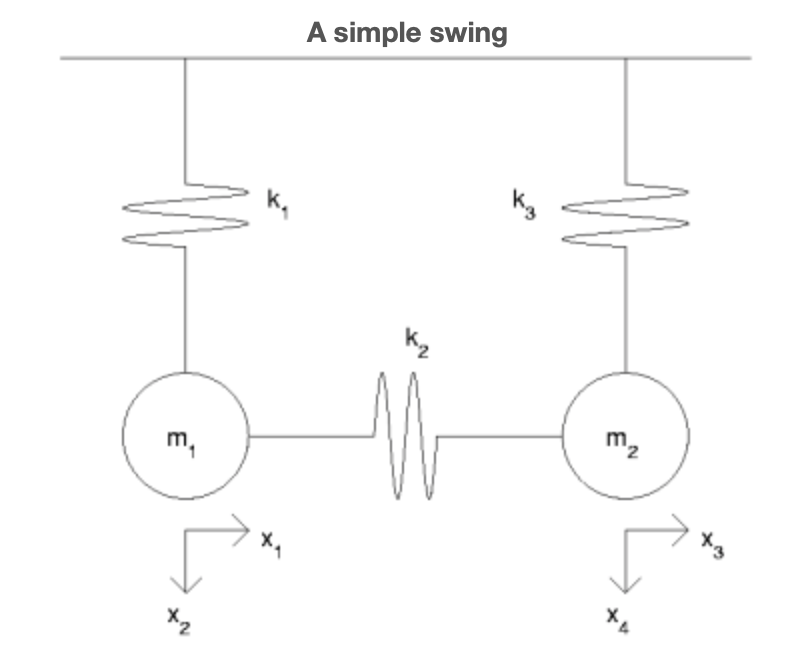
Denotamos por\(x_{1}\) y\(x_{2}\) los respectivos desplazamientos horizontales y verticales de\(m_{1}\) (positivo es derecho y abajo). De igual manera,\(f_{1}\) y\(f_{2}\) denotará los componentes asociados de la fuerza. Los desplazamientos y fuerzas correspondientes a\(m_{2}\) serán denotados por\(x_{3}, x_{4}\) y\(f_{3}, f_{4}\) Al calcular los alargamientos de los tres muelles haremos referencia a sus longitudes no estiradas,\(L_{1}, L_{2}\) y\(L_{3}\)

Ahora, si el resorte 1 se conecta\(\{0, -L_{1}\}\) a\(\{0, 1\}\) cuando está en reposo y\(\{0, -L_{1}\}\) a\(\{x_{1}, x_{2}\}\) cuando se estira, entonces su elongación es simplemente

\[e_{1} = \sqrt{2x_{1}^{2}+(x_{2}+L_{1})^2}-L_{1} \nonumber\]

El precio que uno paga por pasar a dimensiones más altas es que las longitudes ahora se expresan en términos de raíces cuadradas. El resultado es que los alargamientos no son combinaciones lineales de los desplazamientos finales como lo fueron en el caso uniaxial. Si presumimos, sin embargo, que las cargas y rigideces están emparejadas en el sentido de que los desplazamientos son pequeños en comparación con las longitudes originales, entonces podemos ignorar efectivamente la contribución no lineal en la ecuación. Para hacer esto preciso solo necesitamos recordar el desarrollo Taylor de la raíz cuadrada de\((1+t)\)

El desarrollo de Taylor de\(\sqrt{21+t}\) aproximadamente\(t = 0\) es

\[\sqrt{21+t} = 1+\frac{t}{2}+O(t^2) \nonumber\]

donde este último término significa el resto.

Con respecto a\(e_{1}\) esto permite

\[e_{1} = \sqrt{2x_{1}^{2}+x_{2}^{2}+2x_{2}L_{1}+L_{1}^2}-L_{1} \nonumber\]

\[= L_{1} \sqrt{21+\frac{x_{1}^{2}+x_{2}^{2}}{L_{1}^{2}}+\frac{2x_{2}}{L_{1}}}-L_{1} \nonumber\]

\[e_{1} = L_{1}+\frac{x_{1}^{2}+x_{2}^{2}}{2L_{1}^{2}}+x_{2}+L_{1}O((\frac{x_{1}^{2}+x_{2}^{2}}{L_{1}^{2}}+\frac{2x_{2}}{L_{1}})^{2})-L_{1} \nonumber\]

\[= \frac{x_{1}^{2}+x_{2}^{2}}{2L_{1}^{2}}+x_{2}+L_{1}O((\frac{x_{1}^{2}+x_{2}^{2}}{L_{1}^{2}}+\frac{2x_{2}}{L_{1}})^{2}) \nonumber\]

Si ahora asumimos que

\(\frac{x_{1}^{2}+x_{2}^{2}}{L_{1}^{2}}\)es pequeño en comparación con\(x_{2}\)

entonces, como el término O es aún menor, podemos descuidar todos menos los primeros términos en lo anterior y así llegar a

\[e_{1} = x_{2} \nonumber\]

Para tomar un ejemplo concreto, si\(L_{1}\) es un metro y\(x_{1}\) y\(x_{2}\) son cada uno un centímetro, entonces\(x_{2}\) es cien veces\(\frac{x_{1}^{2}+x_{2}^{2}}{L_{1}^{2}}\).

Con respecto al segundo resorte, argumentando lo anterior, su elongación es (aproximadamente) su estiramiento a lo largo de su dirección inicial. Como su dirección inicial es horizontal, su alargamiento es solo la diferencia de los respectivos desplazamientos finales horizontales, a saber,

\[e_{2} = x_{3}-x_{1} \nonumber\]

Finalmente, el alargamiento del tercer resorte es (aproximadamente) la diferencia de sus respectivos desplazamientos extremos verticales, es decir,

\[e_{3} = x_{4} \nonumber\]

Codificamos estos tres alargamientos en

\[\begin{array}{ccc} {\textbf{e} = A \textbf{x}}&{where}&{A = \begin{pmatrix} {0}&{1}&{0}&{0}\\ {-1}&{0}&{1}&{0}\\ {0}&{0}&{0}&{1} \end{pmatrix}} \nonumber \end{array}\]

La Ley de Hooke [1]es una pieza elemental de la física y no se ve perturbada por nuestro salto de estructuras uniaxiales a biaxiales. El resultado es que la fuerza restauradora en cada resorte sigue siendo proporcional a su elongación, es decir,\(y_{j} = k_{j}e_{j}\) donde\(k_{j}\) está la rigidez del muelle j. En términos matriciales,

\[\begin{array}{ccc} {\textbf{y} = K \textbf{e}}&{where}&{K = \begin{pmatrix} {k_{1}}&{0}&{0}\\ {0}&{k_{2}}&{0}\\ {0}&{0}&{k_{3}} \end{pmatrix}} \nonumber \end{array}\]

Equilibrar las fuerzas horizontales y verticales en\(m_{1}\) trae

\[(-y_{2})-f_{1} = 0 \nonumber\]

y

\[y_{1}-f_{2} = 0 \nonumber\]

mientras que el equilibrio de las fuerzas horizontales y verticales en\(m_{2}\) trae

\[y_{2}-f_{3} = 0 \nonumber\]

y

\[y_{3}-f_{4} = 0 \nonumber\]

Los ensamblamos en

\[\begin{array}{ccc} {\textbf{B}y = \textbf{f}}&{where}&{\begin{pmatrix} {0}&{-1}&{0}\\ {1}&{0}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{1} \end{pmatrix}} \nonumber \end{array}\]

y reconocer, como era de esperar, que BB no es más que\(A^{T}\). Al juntar las piezas, encontramos que\(\textbf{x}\) deben satisfacer\(S \textbf{⁢x} = \textbf{f}\) donde

\[S = A^{T} KA = \begin{pmatrix} {k_{2}}&{0}&{-k_{2}}&{0}\\ {0}&{k_{1}}&{0}&{0}\\ {-k_{2}}&{0}&{k_{2}}&{0}\\ {0}&{0}&{0}&{k_{3}} \end{pmatrix} \nonumber\]

Aplicar un paso de Eliminación Gaussiana trae

\[\begin{pmatrix} {k_{2}}&{0}&{-k_{2}}&{0}\\ {0}&{k_{1}}&{0}&{0}\\ {0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{k_{3}} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}}\\ {x_{3}}\\ {x_{4}} \end{pmatrix} = \begin{pmatrix} {f_{1}}\\ {f_{2}}\\ {f_{1}+f_{3}}\\ {f_{4}} \end{pmatrix} \nonumber\]

y la sustitución posterior entrega

\[x_{4} = \frac{f_{4}}{k_{3}} \nonumber\]

\[0 = f_{1}+f_{3} \nonumber\]

\[x_{2} = \frac{f_{2}}{k_{1}} \nonumber\]

\[x_{1}-x_{3} = \frac{f_{1}}{k_{2}} \nonumber\]

El segundo de estos es notable en el sentido de que no contiene componentes de\(\textbf{x}\). En cambio, proporciona una condición sobre\(\textbf{f}\). En términos mecánicos, establece que no puede haber equilibrio a menos que las fuerzas horizontales sobre las dos masas sean iguales y opuestas. Por supuesto, se podría haber observado esto directamente desde el trazado de la armadura. En las estructuras modernas tridimensionales con miles de miembros destinados a albergar o transmitir a los humanos no se debe, sin embargo, estar satisfecho con la integridad `visual' de la estructura. En particular, se desea una descripción detallada de todas las cargas que pueden, y, especialmente, todas las cargas que no pueden, ser equilibradas por el truss propuesto. En términos algebraicos, dada una matriz\(S\), se desea una caracterización de

1. todos aquellos\(\textbf{f}\) para los que\(S \textbf{⁢x} = \textbf{f}\) posee una solución
2. todos aquellos\(\textbf{f}\) para los que\(S \textbf{⁢x} = \textbf{f}\) no posee una solución

Eventualmente proporcionaremos tal caracterización en nuestra discusión posterior sobre el espacio de columna de una matriz.

Suponiendo ahora que\(f_{1}+f_{3} = 0\) observamos que aunque el sistema anterior es consistente aún no logra determinar de manera única los cuatro componentes de\(\textbf{x}\). En particular, especifica solo la diferencia entre\(x_{1}\) y\(x_{3}\) Como resultado ambos

\[\begin{array}{ccc} {\textbf{x} = \begin{pmatrix} {\frac{f_{1}}{k_{2}}}\\ {\frac{f_{2}}{k_{1}}}\\ {0}\\ {\frac{f_{4}}{k_{3}}} \end{pmatrix}}&{and}&{\textbf{x} = \begin{pmatrix} {0}\\ {\frac{f_{2}}{k_{1}}}\\ {-\frac{f_{1}}{k_{2}}}\\ {\frac{f_{4}}{k_{3}}} \end{pmatrix}} \nonumber \end{array}\]

satisfacer\(S \textbf{⁢x} = \textbf{f}\)

\[\begin{pmatrix} {1}\\ {0}\\ {1}\\ {0} \end{pmatrix} \nonumber\]

y aún así tener una solución de\(S \textbf{⁢x} = \textbf{f}\). Buscando la fuente de esta falta de singularidad observamos algunas redundancias en las columnas de S. En particular, la tercera es simplemente lo contrario de la primera. Como es S simplemente\(A^{T}KA\), donde de nuevo, las columnas primera y tercera son opuestas. Estas redundancias están codificadas\(\textbf{z}\) en el sentido de que

\[A \textbf{z} = \textbf{0} \nonumber\]

Interpretando esto en términos mecánicos, vemos\(\textbf{z}\) como un desplazamiento y\(A \textbf{⁢z}\) como el alargamiento resultante. En

\[A \textbf{z} = \textbf{0} \nonumber\]

vemos un desplazamiento distinto de cero produciendo elongación cero. Se dice en este caso que el truss se deforma sin hacer ningún trabajo y habla de ello\(\textbf{z}\) como un modo inestable. Nuevamente, este modo podría haberse observado con una simple mirada a la Figura. Tal no es el caso de estructuras más complejas y así el ingeniero busca un medio sistemático por el cual se puedan identificar todos los modos inestables. Veremos más adelante que todos estos modos son capturados por el espacio nulo de\(A\).

Desde

\[S \textbf{z} = \textbf{0} \nonumber\]

se deduce fácilmente que\(S\) es singular. Más precisamente, si\(S^{-1}\) existieran entonces\(S^{-1}⁢S \textbf{⁢z}\) equivaldría\(S^{-1} \textbf{⁢0}\) i.e.\(\textbf{z} = \textbf{0}\), contrario a la Ecuación. Como resultado, Matlab fallará en resolver\(S \textbf{⁢x} = \textbf{f}\) incluso cuando\(\textbf{f}\) sea una fuerza que el truss pueda equilibrar. Una salida es usar la pseudo-inversa, como veremos en el módulo de Truss Planal General.