2.3: El Braguero Planar General

Última actualización
Guardar como PDF

Page ID: 113160

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Consideremos ahora algo que se asemeja al problema de prospección mecánica introducido en la introducción de métodos matriciales a métodos matriciales para sistemas mecánicos. En la siguiente figura ofrecemos un modelo mecánico crudo de un tejido plano, digamos, por ejemplo, una muestra extirpada de la pared de una vena.

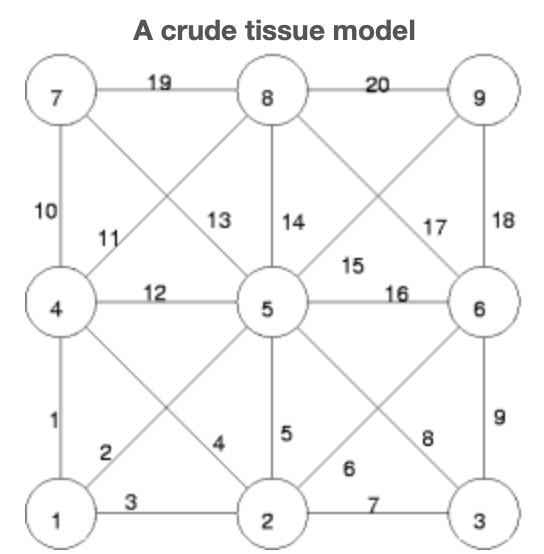
Screen Shot 2020-08-23 a las 9.50.06 PM.png — Figura 1.

Las fibras elásticas, numeradas del 1 al 20, se encuentran en los nodos, numeradas del 1 al 9. Limitamos nuestra observación al movimiento de los nodos denotando los desplazamientos horizontales y verticales del nodo j por$x_{2j-1}$ (horizontal) y$x_{2j}$ (vertical), respectivamente. Reteniendo la convención de que abajo y derecha son positivos observamos que el alargamiento de la fibra 1 es

\[e_{1} = x_{2}-x_{8} \nonumber\]

mientras que el de la fibra 3 es

\[e_{3} = x_{3}-x_{1} \nonumber\].

Como las fibras 2 y 4 no son ni verticales ni horizontales sus alargamientos, en términos de desplazamientos nodales, no son tan fáciles de leer. Esto es más una molestia que un obstáculo, sin embargo, por señalar nuestra discusión sobre el alargamiento en el módulo de celosía plana pequeña, el alargamiento es aproximadamente solo el estiramiento a lo largo de su eje no deformado. Con respecto a la fibra 2, ya que hace el ángulo$-\frac{\pi}{4}$ con respecto al eje horizontal positivo, encontramos

\[e_{2} = x_{9} \cos(-\frac{\pi}{4})-x_{10} \sin(-\frac{\pi}{4}) = \frac{x_{9}-x_{1}+x_{2}-x_{10}}{\sqrt{22}} \nonumber\]

Del mismo modo, como la fibra 4 hace el ángulo$-\frac{3 \pi}{4}$ con respecto al eje horizontal positivo, su elongación es

\[e_{4} = x_{7} \cos(-\frac{3\pi}{4})-x_{8} \sin(-\frac{3\pi}{4}) = \frac{x_{3}-x_{7}+x_{4}-x_{8}}{\sqrt{22}} \nonumber\]

Estas son ambas aplicaciones directas de la fórmula general

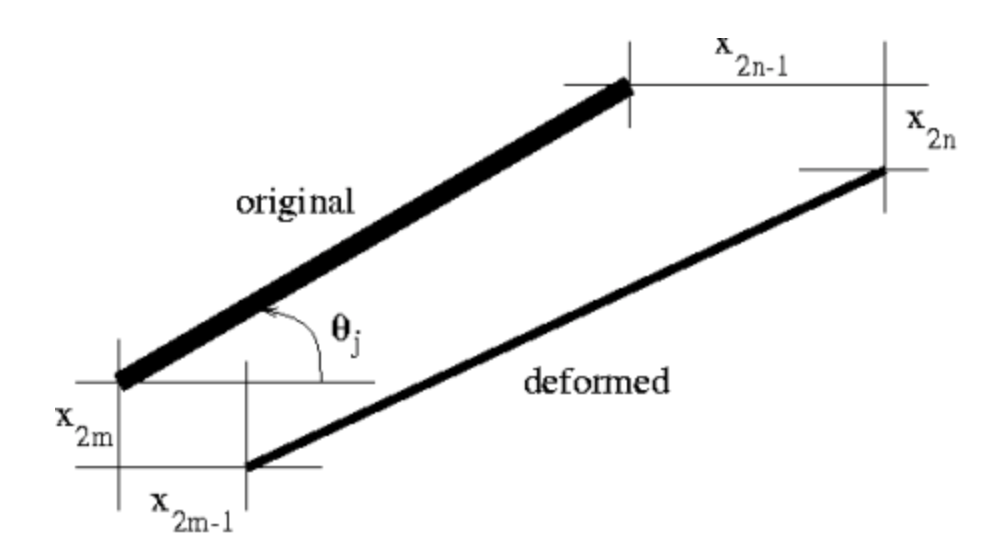
\[e_{j} = x_{2n-1} \cos(\theta_{j})-x_{2n} \sin(\theta_{j}) \nonumber\]

para fibra j Figura a continuación, conectando el nodo mm al nodo nn y haciendo el ángulo$\theta_{j}$ con el eje horizontal positivo cuando$m$ se supone que el nodo se encuentra en el punto$(0, 0)$. El lector debe comprobar que nuestras expresiones para$e_{1}$ y de$e_{3}$ hecho se ajustan a esta fórmula general y eso$e_{2}$ y$e_{4}$ concordar con la intuición de unos. Por ejemplo, la inspección visual del espécimen sugiere que no se puede suponer que la fibra 2 se estire (es decir, tenga positivo$e_{2}$) a menos que$x_{9} > x_{1}$ y/o$x_{2} > x_{10}$. ¿Esto concuerda con la ecuación?

Screen Shot 2020-08-23 a las 9.59.04 PM.png — Figura 2. Elongación de una barra genérica, ver Ecuación.

Aplicando Ecuación a cada una de las fibras restantes llegamos$\textbf{e} = A\textbf{⁢x}$ donde$A$ es de 20 por 18, una fila por cada fibra y una columna por cada grado de libertad. Para sistemas de tal tamaño con una estructura tan bien definida, naturalmente se espera automatizar la construcción. Eso lo hemos hecho precisamente en el archivo M y diario que lo acompañan. El archivo M comienza con una matriz de datos sin procesar que cualquier persona con un transportador podría haber ingresado directamente desde la Figura 1. :

$Screen Shot 2020-08-23 a las 10.01.52 PM.png$

Este dato es precisamente lo que requiere Euqation para saber qué columnas de$A$ recibir el propio$\cos$ o$\sin$. La$A$ matriz final se muestra en el diario.

Los dos pasos siguientes ya son familiares. Si$K$ denota la matriz diagonal de las rigideces de la fibra y$\textbf{f}$ denota el vector de fuerzas nodales entonces

\[\begin{array} {ccc} {\textbf{y} = K \textbf{e}}&{and}&{A^{T} \textbf{y} = \textbf{f}} \nonumber \end{array}\]

y así uno debe resolver$S \textbf{⁢x} = \textbf{f}$ dónde$S = A^{T}KA$. En este caso hay una clase entera tridimensional de$\textbf{z}$ para la cual$A \textbf{⁢z} = \textbf{0}$ y$S \textbf{⁢z} = \textbf{0}$ por lo tanto, por ejemplo, dos traslaciones y una rotación. Como resultado$S$ es singular y x = S\ f en MATLAB no nos llevará a ninguna parte. La salida es reconocer que$S$ tiene modos$18-3 = 15$ estables y que si restringimos$S$ a 'actuar' sólo en estas direcciones entonces 'debería' ser invertible. Comenzaremos a precisar estas nociones en discusiones sobre el Teorema Fundamental del Álgebra Lineal. Por ahora notemos que cada matriz posee tal pseudo-inversa y que puede ser calculada en MATLAB a través del comando pinv. Supongamos que las rigideces de la fibra para cada una sean una y la tracción del borde sea de la forma

\[\textbf{f} =\begin{pmatrix} {-1}&{1}&{0}&{1}&{1}&{1}&{-1}&{0}&{0}&{0}&{1}&{0}&{-1}&{-1}&{0}&{-1}&{1}&{-1} \end{pmatrix}^T \nonumber\],

llegamos a$\textbf{x}$ via x=pinv (S) *f y ofrecemos por debajo su representación gráfica.