5.1: Fibras nerviosas y el Cuarteto Dinámico Strang

Introducción

Hasta este punto nos hemos preocupado en gran medida por

1. Derivar sistemas lineales de ecuaciones algebraicas (a partir de consideraciones de equilibrio estático) y
2. La solución de tales sistemas a través de la eliminación gaussiana.

En este módulo esperamos comenzar a persuadir al lector de que nuestras herramientas se extienden de manera natural a la clase de procesos dinámicos. Más precisamente, vamos a argumentar que

1. El álgebra matricial juega un papel central en la derivación de modelos matemáticos de sistemas dinámicos y que,
2. Con la ayuda de la transformación de Laplace en un entorno analítico o el método Backward Euler en el ajuste numérico, la eliminación gaussiana produce efectivamente la solución.

Fibras nerviosas y el Cuarteto Dinámico Strang

Recopilación de información

El estímulo eléctrico natural de una fibra nerviosa no es la corriente continua sino una breve ráfaga de corriente, el llamado impulso nervioso. En un entorno tan dinámico, la membrana de la celda se comporta no solo como un conductor con fugas sino también como un separador de carga o condensador.

Figura 1.

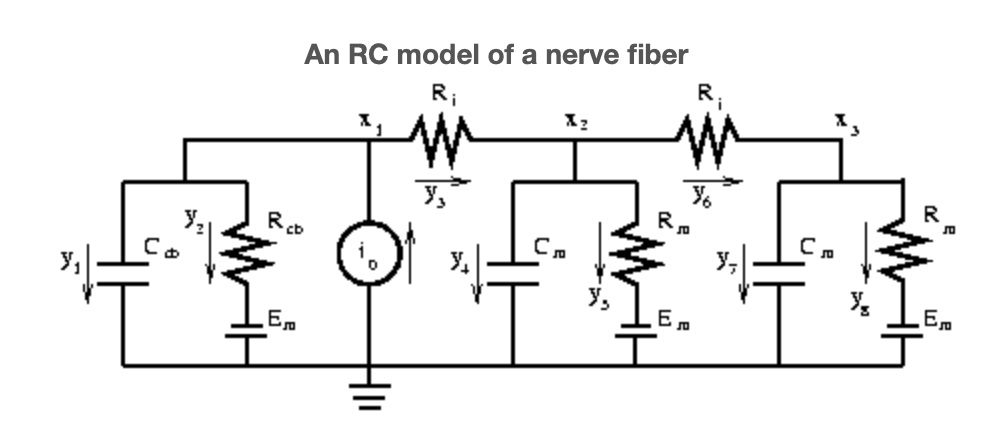
El valor típico de la capacitancia de membrana de una célula es

\[c = 1\frac{\mu F}{cm^{2}} \nonumber\]

donde\(\mu F\) denota Micro-farad. Recordando nuestras convenciones variables, la capacitancia de un solo compartimento es

\[C_{m} = 2 \pi a \frac{l}{N} c \nonumber\]

y corre paralelo a cada uno\(R_{m}\), ver Figura 1. Esta cifra también difiere del circuito más simple del módulo introductorio de modelado eléctrico en que posee dos bordes a la izquierda de los estímulos. Estos bordes sirven para imitar esa porción de la corriente de estímulo que es derivada por el cuerpo celular. Si\(A_{cb}\) denota la superficie del cuerpo celular, entonces tiene

Definición: Capacitancia del cuerpo celular

\(C_{cb} = A_{cb} c\)

Definición: Resistencia del Cuerpo Celular

\(R_{cb} = A_{cb} \rho_{m}\)

Actualización del Cuarteto Strang

Nos preguntamos ahora cómo debería aumentarse el Cuarteto Strang estático del módulo eléctrico introductorio.

Actualización (S1')

Respecto a (S1') procedemos como antes. Las caídas de voltaje son

\[e_{1} = x_{1} \nonumber\]

\[e_{2} = x_{1}-E_{m} \nonumber\]

\[e_{3} = x_{1}-x_{2} \nonumber\]

\[e_{4} = x_{2} \nonumber\]

\[e_{5} = x_{2}-E_{m} \nonumber\]

\[e_{6} = x_{2}-x_{3} \nonumber\]

\[e_{7} = x_{3} \nonumber\]

\[e_{8} = x_{3}-E_{m} \nonumber\]

y así

\[\begin{array}{ccccc} {\textbf{e} = \textbf{b}-A \textbf{x}}&{\text{where}}&{\textbf{b} = (-E_{m}) \begin{pmatrix} {0}\\ {1}\\ {0}\\ {0}\\ {1}\\ {0}\\ {0}\\ {1} \end{pmatrix}}&{\text{and}}&{A = \begin{pmatrix} {-1}&{0}&{0}\\ {-1}&{0}&{0}\\ {-1}&{1}&{0}\\ {0}&{-1}&{0}\\ {0}&{-1}&{0}\\ {0}&{-1}&{1}\\ {0}&{0}&{-1}\\ {0}&{0}&{-1} \end{pmatrix}} \end{array} \nonumber\]

Actualización (S2)

Para actualizar (S2) ahora debemos aumentar la ley de Ohm con

Definición: Ley de voltaje-corriente obedecida por un condensador

La corriente a través de un condensador es proporcional a la tasa de cambio de tiempo del potencial a través de él.

Esto produce, (denotando derivado por '),

\[y_{1} = C_{cb}e_{1}′ \nonumber\]

\[y_{2} = \frac{e_{2}}{R_{cb}} \nonumber\]

\[y_{3} = \frac{e_{3}}{R_{i}} \nonumber\]

\[y_{4} = C_{m}e_{4}′ \nonumber\]

\[y_{5} = \frac{e_{5}}{R_{m}} \nonumber\]

\[y_{6} = \frac{e_{6}}{R_{i}} \nonumber\]

\[y_{7} = C_{m} e_{7}′ \nonumber\]

\[y_{8} = \frac{e_{8}}{R_{m}} \nonumber\]

o, en términos matriciales,

\[\textbf{y} = G \textbf{e}+C \textbf{e}' \nonumber\]

donde

\[G = \begin{pmatrix} {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{\frac{1}{R_{cb}}}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}} \end{pmatrix} \nonumber\]

y

\[C = \begin{pmatrix} {C_{cb}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0} \end{pmatrix} \nonumber\]

son las matrices de conductancia y capacitancia.

Actualización (S3)

Como la Ley Actual de Kirchhoff es insensible al tipo de dispositivo que ocupa un borde, el paso (S3) procede exactamente como antes.

\[i_{0}-y_{1}-y_{2}-y_{3} = 0 \nonumber\]

\[y_{3}-y_{4}-y_{5}-y_{6} = 0 \nonumber\]

\[y_{6}-y_{7}-y_{8} = 0 \nonumber\]

o, en términos matriciales,

\[\begin{array}{ccc} {A^{T} \textbf{y} = -\textbf{f}}&{where}&{\textbf{f} = \begin{pmatrix} {i_{0}}\\ {0}\\ {0} \end{pmatrix}^{T}} \end{array} \nonumber\]

Paso (S4): Ensamblar

El paso (S4) sigue siendo uno de montaje,

\[(A^{T} \textbf{y} = -\textbf{f}) \Rightarrow (A^{T} (G \textbf{e}+C \textbf{e}') = -\textbf{f}) \Rightarrow (A^{T} (G(\textbf{b}-A\textbf{x})+C (\textbf{b}'-A\textbf{x}')) = -\textbf{f}) \nonumber\]

se convierte

\[A^{T}CA \textbf{x}'+A^{T}GA \textbf{x} = A^{T}G \textbf{b}+\textbf{f}+A^{T}C \textbf{b}' \nonumber\]

Esta es la forma general de las ecuaciones potenciales para un circuito RC. Se presume que el usuario conoce el valor inicial de cada uno de los potenciales,

\[\textbf{x}(0) = X \nonumber\]

En cuanto al circuito de la Figura 1, y dejando\(G = \frac{1}{R}\), encontramos

\[\begin{array}{cc} {A^{T}CA = \begin{pmatrix} {C_{cb}}&{0}&{0}\\ {0}&{C}&{0}\\ {0}&{0}&{C} \end{pmatrix}}&{A^{T}CA = \begin{pmatrix} {G_{cb}+G_{i}}&{-G_{i}}&{0}\\ {-G_{i}}&{2G_{i}+G_{m}}&{-G_{i}}\\ {0}&{-G_{i}}&{G_{i}+G_{m}} \end{pmatrix}} \end{array} \nonumber\]

\[\begin{array}{cc} {A^{T}G \textbf{b} = E_{m} \begin{pmatrix} {G_{cb}}\\ {G_{m}}\\ {G_{m}} \end{pmatrix}}&{A^{T}C \textbf{b}' = \begin{pmatrix} {0}\\ {0}\\ {0} \end{pmatrix}} \end{array} \nonumber\]

y un potencial inicial (descanso) de

\[x_{0} = E_{m} \begin{pmatrix} {1}\\ {1}\\ {1} \end{pmatrix}^{T} \nonumber\]

Modos de Ataque

Ahora vamos a esbozar dos modos de ataque a tales problemas. Laplace Transform es una herramienta analítica que produce soluciones exactas y cerradas para sistemas manejables pequeños y, por lo tanto, ofrece información sobre cómo “deberían” comportarse los sistemas más grandes. El método Backward-Euler es una técnica para resolver una versión discretizada (y por tanto aproximada) de la Ecuación. Es altamente flexible, fácil de codificar y funciona en problemas de gran tamaño. Tanto los métodos Backward-Euler como Laplace Transform requieren, en su esencia, la solución algebraica de un sistema lineal de ecuaciones. Al derivar estos métodos nos resultará más conveniente proceder del sistema genérico

\[\textbf{x}′ = B\textbf{x}+\textbf{g} \nonumber\]

Con respecto a nuestro problema de fibra

\[B = (-(A^{T}CA)^{-1}) A^{T}GA \nonumber\]

\[= \begin{pmatrix} {\frac{-(G_{cb}+G_{i})}{C_{cb}}}&{\frac{G_{i}}{C_{cb}}}&{0}\\ {\frac{G_{i}}{C_{m}}}&{\frac{-(2G_{i}+G_{m})}{C_{m}}}&{\frac{G_{i}}{C_{m}}}\\ {0}&{\frac{G_{i}}{C_{m}}}&{\frac{-(G_{i}+G_{m})}{C_{m}}} \end{pmatrix} \nonumber\]

y

\[\textbf{g} = (A^{T}CA)^{-1}(A^{T}G \textbf{b}+\textbf{f}) = \begin{pmatrix} {\frac{G_{cb}E_{m}+i_{0}}{C_{cb}}}\\ {\frac{E_{m}G_{m}}{C_{m}}}\\ {\frac{E_{m}G_{m}}{C_{m}}} \end{pmatrix} \nonumber\]