4.1: Vectores en R
- Page ID
- 114536
- Encuentra el vector de posición de un punto en\(\mathbb{R}^n\).
La notación\(\mathbb{R}^{n}\) se refiere a la colección de listas ordenadas de números\(n\) reales, es decir\[\mathbb{R}^{n} = \left\{ \left( x_{1}\cdots x_{n}\right) :x_{j}\in \mathbb{R}\text{ for }j=1,\cdots ,n\right\}\nonumber \] En este capítulo, echamos un vistazo más de cerca a los vectores en\(\mathbb{R}^n\). Primero, consideraremos lo que\(\mathbb{R}^n\) parece con más detalle. Recordemos que el punto dado por\(0=\left( 0, \cdots, 0 \right)\) se llama el origen.
Ahora, consideremos el caso de\(\mathbb{R}^n\) for\(n=1.\) Entonces a partir de la definición podemos identificarnos\(\mathbb{R}\) con puntos de la siguiente manera:\[\mathbb{R} = \mathbb{R}^{1}= \left\{ \left( x_{1}\right) :x_{1}\in \mathbb{R} \right\}\nonumber \] De ahí,\(\mathbb{R}\) se define como el conjunto de todos los números reales y geométricamente, podemos describir esto como todos los puntos en una línea.\(\mathbb{R}^{1}\)
Ahora supongamos\(n=2\). Entonces, a partir de la definición,\[\mathbb{R}^{2}= \left\{ \left(x_{1}, x_{2}\right) :x_{j}\in \mathbb{R}\text{ for }j=1,2 \right\}\nonumber \] Considera el plano coordenado familiar, con un\(x\) eje y un\(y\) eje. Cualquier punto dentro de este plano de coordenadas se identifica por dónde se encuentra a lo largo del\(x\) eje, y también por dónde se encuentra a lo largo del\(y\) eje. Considera como ejemplo el siguiente diagrama.
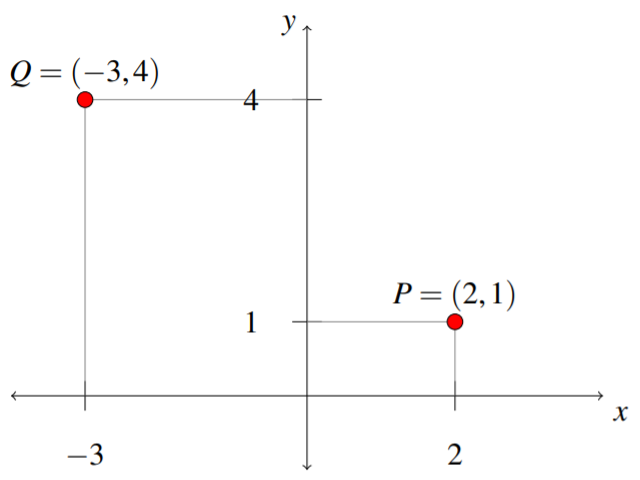
De ahí que cada elemento en\(\mathbb{R}^2\) sea identificado por dos componentes,\(x\) y\(y\), de la manera habitual. Las coordenadas\(x, y\) (o\(x_1\),\(x_2\)) determinan de manera única un punto en el plano. Tenga en cuenta que si bien la definición usa\(x_1\) y\(x_2\) para etiquetar las coordenadas y usted puede estar acostumbrado a\(x\) y\(y\), estas notaciones son equivalentes.
Ahora supongamos\(n=3\). Es posible que haya encontrado previamente el sistema de coordenadas\(3\) -dimensional, dado por\[\mathbb{R}^{3}= \left\{ \left( x_{1}, x_{2}, x_{3}\right) :x_{j}\in \mathbb{R}\text{ for }j=1,2,3 \right\}\nonumber \]
Los puntos en\(\mathbb{R}^3\) estarán determinados por tres coordenadas, a menudo escritas\(\left(x,y,z\right)\) que corresponden a los\(z\) ejes\(x\)\(y\),, y. Podemos pensar como arriba que las dos primeras coordenadas determinan un punto en un plano. El tercer componente determina la altura por encima o por debajo del plano, dependiendo de si este número es positivo o negativo, y todos juntos esto determina un punto en el espacio. Se ve que las triples ordenadas corresponden a puntos en el espacio así como los pares ordenados corresponden a puntos en un plano y los números reales individuales corresponden a puntos en una línea.
La idea detrás de lo más general\(\mathbb{R}^n\) es que podemos extender estas ideas más allá de\(n = 3.\) esta discusión respecto a puntos en\(\mathbb{R}^n\) conduce a un estudio de vectores en\(\mathbb{R}^n\). Si bien consideramos\(\mathbb{R}^n\) para todos\(n\), nos centraremos en gran medida\(n=2,3\) en esta sección.
Considera la siguiente definición.
Dejar\(P=\left( p_{1},\cdots ,p_{n}\right)\) ser las coordenadas de un punto en\(\mathbb{R}^{n}.\) Entonces el vector\(\overrightarrow{0P}\) con su cola en\(0=\left( 0,\cdots ,0\right)\) y su punta en\(P\) se llama el vector de posición del punto\(P\). Escribimos\[\overrightarrow{0P} = \left [ \begin{array}{c} p_{1} \\ \vdots \\ p_{n} \end{array} \right ]\nonumber \]
Por esta razón podemos escribir\(P=\left( p_{1},\cdots ,p_{n}\right) \in \mathbb{R}^{n}\) tanto como\(\overrightarrow{0P} = \left [ p_{1} \cdots p_{n} \right ]^T \in \mathbb{R}^{n}\).
Esta definición se ilustra en el siguiente cuadro para el caso especial de\(\mathbb{R}^{3}\).
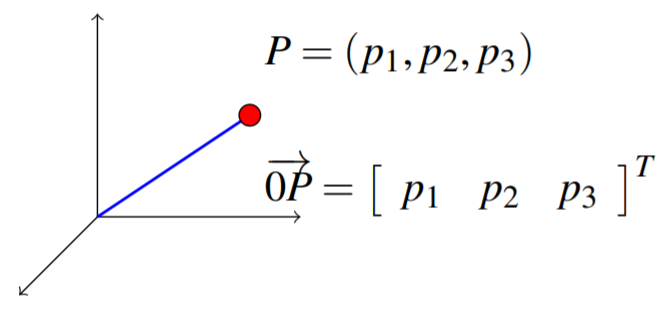
Así cada punto\(P\) en\(\mathbb{R}^{n}\) determina su vector de posición\(\overrightarrow{0P}\). Por el contrario, cada vector de posición\(\overrightarrow{0P}\) que tiene su cola en\(0\) y punto en\(P\) determina el punto\(P\) de\(\mathbb{R}^{n}\).
Ahora supongamos que se nos dan dos puntos,\(P,Q\) cuyas coordenadas son\(\left( p_{1},\cdots ,p_{n}\right)\) y\(\left( q_{1},\cdots ,q_{n}\right)\) respectivamente. También podemos determinar el vector de posición de\(P\) a\(Q\) (también llamado el vector de\(P\) a\(Q\)) definido de la siguiente manera. \[\overrightarrow{PQ} = \left [ \begin{array}{c} q_{1}-p_{1}\\ \vdots \\ q_{n}-p_{n} \end{array} \right ] = \overrightarrow{0Q} - \overrightarrow{0P}\nonumber \]
Ahora, imagina tomar un vector\(\mathbb{R}^n\) y moverlo alrededor, manteniéndolo siempre apuntando en la misma dirección que se muestra en la siguiente imagen.
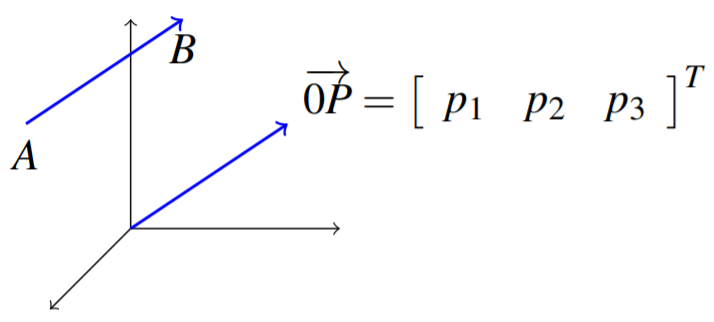
Después de moverlo, se le considera como el mismo vector. Cada vector,\(\overrightarrow{0P}\) y\(\overrightarrow{AB}\) tiene la misma longitud (o magnitud) y dirección. Por lo tanto, son iguales.
Consideremos ahora la definición general de un vector en\(\mathbb{R}^n\).
Let\(\mathbb{R}^{n} = \left\{ \left( x_{1}, \cdots, x_{n}\right) :x_{j}\in \mathbb{R}\text{ for }j=1,\cdots ,n\right\} .\) Then,\[\vec{x} = \left [ \begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array} \right ]\nonumber \] se llama vector. Los vectores tienen tanto tamaño (magnitud) como dirección. Los números\(x_{j}\) se llaman los componentes de\(\vec{x}\).
Usando esta notación, podemos usar\(\vec{p}\) para denotar el vector de posición del punto\(P\). Observe que en este contexto,\(\vec{p} = \overrightarrow{0P}\). Estas notaciones se pueden usar indistintamente.
Se puede pensar en los componentes de un vector como indicaciones para obtener el vector. Considerar\(n=3\). Dibuja un vector con su cola en el punto\(\left( 0,0,0\right)\) y su punta en el punto\(\left( a,b,c\right)\). Este vector se obtiene iniciando en\(\left( 0,0,0\right)\), moviéndose paralelo al\(x\) eje hacia\(\left( a,0,0\right)\) y luego desde aquí, moviéndose paralelo al\(y\) eje hasta\(\left( a,b,0\right)\) y finalmente paralelo al\(z\) eje para\(\left( a,b,c\right).\) Observar que el mismo vector resultaría si comenzaras en el punto \(\left( d,e,f \right)\), se movió paralelo al\(x\) eje para\(\left( d+a,e,f\right) ,\) luego paralelo al\(y\) eje a\(\left( d+a,e+b,f\right) ,\) y finalmente paralelo al\(z\) eje a\(\left( d+a,e+b,f+c\right)\). Aquí, el vector tendría su cola sentada en el punto determinado por\(A= \left( d,e,f\right)\) y su punto en\(B=\left( d+a,e+b,f+c\right) .\) Es el mismo vector porque apuntará en la misma dirección y tendrá la misma longitud. Es como si tomaras una flecha real, y la moviste de un lugar a otro manteniéndola apuntando en la misma dirección.
Concluimos esta sección con una breve discusión sobre la notación. En secciones anteriores, hemos escrito vectores como columnas, o\(n \times 1\) matrices. Por conveniencia en este capítulo podemos escribir vectores como la transposición de vectores de fila, o\(1 \times n\) matrices. Estos son por supuesto equivalentes y podemos movernos entre ambas notaciones. Por lo tanto, reconocer que\[\left [ \begin{array}{r} 2 \\ 3 \end{array} \right ] = \left [ \begin{array}{rr} 2 & 3 \end{array} \right ]^T\nonumber \]
Observe que dos vectores\(\vec{u} = \left [ u_{1} \cdots u_{n}\right ]^T\) y\(\vec{v}=\left [ v_{1} \cdots v_{n}\right ]^T\) son iguales si y sólo si todos los componentes correspondientes son iguales. Precisamente,\[\begin{array}{c} \vec{u}=\vec{v} \; \mbox{if and only if}\\ u_{j}=v_{j} \; \mbox{for all}\; j=1,\cdots ,n \end{array}\nonumber \] Así\(\left [ \begin{array}{rrr} 1 & 2 & 4 \end{array} \right ]^T \in \mathbb{R}^{3}\) y\(\left [ \begin{array}{rrr} 2 & 1 & 4 \end{array} \right ]^T \in \mathbb{R}^{3}\) pero\(\left [ \begin{array}{rrr} 1 & 2 & 4 \end{array} \right ]^T \neq \left [ \begin{array}{rrr} 2 & 1 & 4 \end{array} \right ]^T\) porque, a pesar de que están involucrados los mismos números, el orden de los números es diferente.
Para el caso específico de\(\mathbb{R}^3\), hay tres vectores especiales que solemos utilizar. Están dadas por\[\vec{i} = \left [ \begin{array}{rrr} 1 & 0 & 0 \end{array} \right ]^T\nonumber \]\[\vec{j} = \left [ \begin{array}{rrr} 0 & 1 & 0 \end{array} \right ]^T\nonumber \]\[\vec{k} = \left [ \begin{array}{rrr} 0 & 0 & 1 \end{array} \right ]^T\nonumber \] Podemos escribir cualquier vector\(\vec{u} = \left [ \begin{array}{rrr} u_1 & u_2 & u_3 \end{array} \right ]^T\) como una combinación lineal de estos vectores, escritos como\(\vec{u} = u_1 \vec{i} + u_2 \vec{j} + u_3 \vec{k}\). Esta notación se utilizará a lo largo de este capítulo.


